碳排放约束下长江经济带农业绿色生产效率测度及收敛性

徐东芳 孔令成

徐东芳，孔令成. 碳排放约束下长江经济带农业绿色生产效率测度及收敛性［J］. 湖北农业科学，2024，63（3）：142-149．

摘要：运用面板三阶段DEA模型对长江经济带农业绿色生产效率进行测度，并在此基础上进行收敛性分析。结果表明，环境因素和随机误差对长江经济带农业绿色生产效率具有显著影响；长江经济带上游、中游和下游的农业绿色生产效率存在明显的空间不均衡现象；2017—2019年长江经济带三大区域省市间农业绿色生产效率差异呈缩小趋势。基于此，为了进一步从总体上提高及从空间上优化长江经济带农业绿色生产效率，提出明确地区环境，因地制宜；把握区域差异，精准施策；打破区域壁垒，协同发展的对策。

关键词：碳排放约束；农业绿色生产效率；收敛性；长江经济带

中图分类号：F323.223；X82         文献标识码：A

文章编号：0439-8114（2024）03-0142-08

DOI：10.14088/j.cnki.issn0439-8114.2024.03.022 开放科学（资源服务）标识码（OSID）：

作为中国的重要粮仓，长江经济带过去高强度、粗放式的农业生产模式虽然促进了农业生产产量的增加，但是同时带来了生产资源浪费、面源污染等问题［1］，因此，提高长江经济带农业绿色生产效率迫在眉睫。在转型过程中，长江经济带各省市多措并举提高农业绿色生产效率，但是由于不同省市的经济发展水平、地理位置、资源禀赋、文化习俗等不同，农业绿色生产效率可能存在较大差异。在此背景下，研究长江经济带农业绿色生产效率，对提高长江经济带农业整体竞争力，实现乡村振兴具有重要意义。

国内外学者关于农业绿色生产效率所取得的成果颇丰。理论上，王学婷等［2］对农业绿色低碳发展路径进行了深入探讨；张俊飚等［3］对农业绿色低碳进行了误区鉴定及发展前瞻，为后续研究厘清了边界。实证上，农业绿色生产效率的核心在于将其内涵具象化以及对污染物的处理。大多数学者选择通过构造指标体系来测算农业绿色生产效率，但指标选取的角度与测算方法却不尽相同。从指标选取角度看，国外学者Bravo-Ureta等［4］认为发展中国家农业生产效率主要受农民受教育程度、自有资产和自身经营管理能力的影响；Helfand等［5］认为提高人力资本是提高农业生产效率的关键因素；Monchuk［6］认为科学的价格调控政策能有效提高农业生产效率。与国外学者相比，国内学者更侧重从微观角度选取指标进行研究。有学者认为农药、化肥、农用地膜等投入的减少有助于提高农业绿色生产效率［7］；也有学者从土地、劳动、资本三大要素投入角度测算［8］；还有学者创造性地将种子投入做细分处理［9］。从污染物处理角度看，主要有两种处理方式，一是将污染物看作投入变量，符合投入品越少越好的特征［10］；二是将污染物等“非合意产出”转换为“合意产出”，该方法被大多数学者采用［11-13］。将碳排放等污染物进行非合意产出标记区分，是传统农业效率与农业绿色效率的显著区别。刘亦文等［14］将农业碳排放作为农业污染物进行非期望产出标记，从而测算中国农业绿色全要素生产率。

综上可以看出，现有成果较少将研究区域置于同质环境下分析农业绿色生产效率。长江经济带作为中国重要农业生产区，提高其农业绿色生产效率对促进农业高质量发展、保障国家粮食安全具有重要意义。基于此，本研究以长江经济带11个省市为研究对象，构建面板三阶段DEA模型，综合传统DEA模型与SFA模型的优点，剔除各省市环境因素和随机误差对农业绿色生产效率的影响，测算长江经济带农业绿色生产效率，并对其收敛性进行分析，以期真实准确地评估该区域农业绿色生产效率的发展水平并预测其未来态势，为今后从整体上提高及空间上优化长江经济带农业绿色生产效率提供参考。

1 研究方法

1.1 模型选择

三阶段DEA模型是Fried等［15］在传统DEA模型基础上加以改进提出的能更好地估计决策单元（Decision making unit，DMU）效率的方法。传统DEA模型不能有效剔除环境因素和随机误差项对决策单元效率的影响，无法使决策单元在同质环境下分析，从而使结果失真。而参数随机前沿模型（Stochastic frontier model，SFA）具有解释噪声和研究传统假设检验的优势，且更贴近农业生产特征，因此Fried等［15］将DEA与SFA模型相结合，提出了三阶段DEA模型，此处进一步借鉴刘自敏等［16］的研究成果，采用面板三阶段DEA模型对长江经济带农业绿色生产效率进行探究，具体步骤如下。

1）第一阶段，传统DEA模型。DEA模型能够有效评价决策单元生产效率，其能够在多投入产出的模式下无需构建生产函数估计参数即可度量决策单元之间生产效率的相对有效性。DEA模型主要包括CCR模型和BCC模型，其区别在于假设前提分别为规模报酬不变和规模报酬可变。由于BCC模型的假设更符合实际情况，更具有参考价值，因而第一阶段构建基于投入导向型的BCC模型测算纯技术效率（Vrste）。

2）第二阶段，构建相似SFA模型。利用相似SFA模型可分解第一阶段得出的投入/产出松弛值，假设松弛值只受外部环境因素、随机误差项和管理效率这3部分因素的影响，构建SFA模型可以有效分离这3部分因素，从中提取出仅由管理无效率导致的DMU投入剩余。

为了进一步将随机误差从混合误差项中分离出来，采用罗登跃［17］的方法估计随机误差项。然后使用SFA回归模型分析结果对长江经济带各地区的农业绿色生产效率投入变量进行调整，从而剔除外部环境因素和随机误差项的干扰，使其能够在相同的环境下测算长江经济带各地区农业绿色生产效率。调整后的表达式如式（1）所示。

[XAnit=Xnit+maxfZnit;βnt-fZnit;βnt+maxνnit-νnit]                （1）

式中，[XAnit]、[Xnit]分别为调整后和调整前长江经济带各地区的投入变量；[Znit]为投入松弛变量；[βnt]、[νnit]分别为外部环境变量参数和随机误差项的估计值。[fZnit;βnt]是外部环境变量对投入松弛变量的影响，具体表示为[fZnit;βnt=Znitβnt]，即外部环境变量与投入松弛变量的乘积；[maxfZnit;βnt-fZnit;βnt]表示使长江经济带各决策单元调整至同样的经营环境；[maxνnit-νnit]表示将长江经济带各决策单元的随机干扰调整至相同情形。

3）第三阶段，调整后的DEA模型。利用调整后的投入变量数据[XAnit]替代长江经济带原始投入变量数据[Xnit]，产出仍为长江经济带原始产出数据，再次使用BCC模型评估纯技术效率，进而得到长江经济带各决策单元的农业绿色生产效率（AGPE），即剔除了外部环境变量与随机误差项影响的绿色生产技术效率，能够客观地反映长江经济带各决策单元的农业绿色生产效率。

1.2 数据来源与指标选取

立足于长江经济带农业绿色生产实际，并借鉴刘艳［18］的研究成果，以广义农业为研究对象，并选取该经济带11个省市作为目标区域，所有数据均来自2001—2020年《中国统计年鉴》及各省市统计年鉴。所选取的指标具体如下。

1）投入指标选取。选取土地、劳动、农业机械总动力、农药、化肥和农用地膜作为投入要素［19］。其中，土地为农用土地面积，包括农作物播种面积、水产养殖面积；劳动为第一产业从业总人数；农业机械总动力指用于农业的机械动力之和。

2）产出指标选取。农业生产效率的产出指标主要反映农业所提供农产品的经济价值，因此在研究长江经济带农业绿色生产效率时，选择各地区的农林牧渔业生产总值作为产出指标［20］，为消除物价因素的影响，以2000年为基期做指数平减处理，得出各省市农林牧渔业的实际产出。此外，借鉴吴传清等［21］的研究成果，选择农业碳排放作为非合意产出，并依据李波等［22］的成果对其进行细致测算及相应转化，以期对长江经济带农业绿色生产效率进行有效测度及收敛性分析。

3）环境指标选取。产业结构高度化（ISH），表示各省市在经济发展过程中，第二、第三产业产值之和占地区GDP总值的比重，借鉴张玉昌等［23］的测度方法，计算长江经济带各省市产业结构高度化水平，其值越大表示该地区产业结构高度化水平越高，产业结构趋向成熟；城镇化水平（URB），用人口城镇化比重代替，城镇化水平越高表示地区经济发展水平越好［24］；农村人均用电量（ELE），用农村总用电量除以农村常住人口数表示，用均值表示有利于地区之间的横向对比；农村居民人均可支配收入（INC），以2000年为基期进行指数平减以消除价格因素的影响［19］。

4）Pearson 相关性检验。在实证分析之前，利用Pearson相关性检验对投入变量指标与产出变量指标之间是否满足同向性假设进行验证。采用SPSS 20.0软件进行检验，结果如表 1所示。由表1可知，长江经济带各省市投入变量与产出变量相关系数多数通过了双侧在1%显著水平下的检验，小部分在5%水平下也通过检验，说明构建的指标体系满足同向性假设要求，所选取的投入、产出指标合理，可进行下一步实证分析。

1.3 收敛性分析

经典收敛模型主要包括α收敛和β收敛，其中β收敛的应用更广泛。

1.3.1 α收敛检验 α收敛检验可判定不同省份农业绿色生产效率的差异是否会随时间推移而不断缩小，即各地农业绿色生产效率差异是否会逐渐消失。α收敛检验需要逐年计算不同省市农业绿色生产效率的变异系数（CV），具体计算式如式（2）所示。

[CV=i=1nxit-xt2nxt]                （2）

式中，xit表示i省市t年农业绿色生产效率；[xt]为各省市农业绿色生产效率的均值。CV越大，说明各省市农业绿色生产效率差异越大。

1.3.2 β收敛检验 经典β收敛分为绝对β收敛和条件β收敛，其中绝对β收敛与α收敛都属于绝对收敛，都是判别不同地区农业绿色生产效率增长最终是否达到稳定状态，如果存在绝对β收敛则说明落后的地区在后续的发展中农业绿色生产以较快的速度追上了领先的地区。绝对β收敛检验的计算式如式（3）所示。

[ln（AGPEi，t+1）-ln（AGPEi，t）=α+βln（AGPEi，t）+εi，t]                        （3）

式中，[ln（AGPEi，t+1）-ln（AGPEi，t）] 表示长江经济带第i个省市t+1年农业绿色生产效率对数与第t年的差值；α为常数项；β为回归系数；[εi，t]为随机误差。如果β系数显著为负，则认为存在绝对β收敛。

2 实证结果与分析

2.1 第一阶段传统DEA模型实证结果

运用DEAP2.1软件对长江经济带2000—2019年的农业绿色生产效率水平进行有效测度，因篇幅较长，此处仅展示了2000年、2014年、2019年的结果，具体如表2所示。从长江经济带整体变化幅度看，该区域这3年经济带农业绿色生产综合技术效率和纯技术效率都经历了先降后升的变化，规模效率则先增后减。2000年，国家提出“三农”的概念，将农业、农村、农民问题提高到国家战略高度；2014年，中共中央首次提出长江经济带战略，注重大保护，不搞大开发，因此以上农业绿色生产效率的变化整体符合长经济带农业绿色生产发展实际。由于此结果没有分离环境变量和随机误差对农业绿色生产效率的影响，因而无法精确反映不同省市间的实际环境效率，还需进一步分解测算。

2.2 第二阶段面板相似SFA模型实证结果

将第一阶段得出的决策单元投入松弛值作为因变量，再将所筛选的环境变量作为自变量，代入SFA面板回归模型，利用Stata15软件进行估计，结果如表3所示。从表3可以看出，4个环境变量对投入松弛值的系数大多数通过显著性检验，且管理无效率（μ）除劳动力松弛外均在5%或1%的水平下显著，说明选用的环境变量对长江经济带农业绿色生产效率投入冗余的影响是显著的。农药、农用地膜、化肥、农业机械动力投入松弛的管理无效率与总方差的比值（γ）大于0.50，说明农药、农用地膜、化肥、农业机械动力投入松弛主要受管理因素的影响。相反，劳动力和农用土地面积松弛所对应的γ分别为0.207 4和0.335 1，均小于0.50，说明随机误差对劳动力松弛和农用土地面积松弛的影响占主导地位。因此，构建SFA模型对管理无效率和随机误差进行剥离是有必要的。由结果可知，农村居民实际可支配收入对所有投入松弛变量均具有显著的负效应，说明提高农村居民收入有利于降低投入，提高农业绿色生产效率。人口城镇化对农药、农业机械动力松弛具有显著的正向影响，对劳动力松弛具有显著的负向影响；产业结构高度化只对农药松弛有负向影响；农村人均用电量仅对农药松弛有显著的正向影响。

2.3 第三阶段调整后DEA模型实证结果

把第二阶段得出的系数代入式（1）计算出调整后的投入变量，并结合原始产出变量构建成新的投入产出矩阵，再次代入BCC模型进行计算分析，最终得到第三阶段调整后的长江经济带农业绿色生产综合技术效率、纯技术效率、规模效率和规模报酬状况等，结果如表4所示。2000—2019年长经济带农业绿色生产综合技术效率、纯技术效率、规模效率均处于递增的状态，均在2019年达最大值，且纯技术效率达最佳水平，但规模效率有待进一步提高。

对比表2和表4可知，将外部环境因素和随机误差因素剔除后，长江经济带2000—2019年农业绿色生产的综合技术效率和规模效率大幅度降低，纯技术效率提高。为了进一步分析第一阶段与第三阶段结果的有效性，通常采用Wilcoxon检验进行分析，检验结果如表5所示。由表5可知，长江经济带农业绿色生产效率调整前后均存在显著差异，说明第二阶段对环境因素和随机误差的剥离是有效的，最终使得长江经济带所有省市农业绿色生产处于同质的环境里，因而纯技术效率更能真实地反映长江经济带农业绿色生产效率。

对比表2和表4结果可知，总体而言，与第一阶段相比，第三阶段长江经济带农业绿色生产的综合技术效率和规模效率有所回落，而纯技术效率却有一定的提升。具体来看，农业绿色生产综合技术效率3年所有地区均值从0.809小幅回落至0.729，规模效率从0.975大幅降低至0.731，而纯技术效率的平均水平从0.830上升至0.997，这说明在经营环境和随机误差的影响下，长江经济带农业绿色生产的综合技术效率和规模效率表现虚高，而纯技术效率则出现抑制情况。具体到相关省市，上海市在调整后规模效率出现了大幅下降，2019年从调整前的1.000降到调整后的0.288，成为规模效率最低的区域，其原因是上海市作为全国金融中心大力发展第二、第三产业，第一产业发展总体薄弱，且上海市依托优越的地理位置促使周边城市对其农产品需求补给式供应，才使得上海市农产品市场供求基本稳定，而其农业生产经营规模无法从市场角度得到有效调节。同样的情况也发生在重庆市和贵州省两地，调整后规模效率整体大幅下降。重庆市是有名的山城，贵州省处于云贵高原，种植面积较少，规模效率低是符合实际情况的，进一步佐证了对环境变量进行剥离是合理的。江西省作为长江经济带农业大省，调整后其纯技术效率（2014年、2019年）提高，但规模效率（2000年、2014年、2019年）均有不同程度下降，且下降幅度较大，说明江西省绿色生产效率较高，但是规模效率较低，需进一步扩大农业绿色生产规模。江苏、浙江、安徽、湖北和四川5省2019年在调整前后纯技术效率均为1.000，说明这5个省的农业绿色生产属于较高水平。云南省2019年调整前后纯技术效率均为1.000，规模效率从0.889提高至0.916，说明环境使云南省的规模效率被低估；类似情况的还有湖南省，2019年调整前后湖南省纯技术效率从0.974提高至1.000，规模效率从0.968提高至0.971，综合技术效率从0.942提高至0.970，说明环境使湖南省的绿色生产效率和规模效率被低估，导致湖南省的技术效率被低估。

2.4 收敛性分析

通过上述分析可知长江经济带农业绿色生产效率在空间上存在差异，因此，把考察样本划分为上游（云南省、贵州省、四川省、重庆市）、中游（湖南省、湖北省、江西省）和下游（安徽省、浙江省、江苏省、上海市）3个区域进行研究。为进一步分析差异性的具体情况和未来发展趋势，借鉴沈洋等［25］、李欠男等［26］的研究，引入收敛性分析。

2.4.1 α收敛检验 根据式（2）计算得出长江经济带11个省市的变异系数。随着时间的推移，若CV小于前一年的，则存在α收敛，反之表示发散。由图1可知，2000—2019年，总体变异系数呈先下降后上升再下降最后平稳的趋势。2002—2004年，总体和各区域变异系数波动幅度较大，原因可能是2000年国家正式提出“三农”概念，重视农业问题，探索农业发展，故此阶段长江经济带农业绿色生产效率变异系数波动较大，符合国情。2006年，中国废止了农业税，大力发展农业，此后农业进入平稳发展阶段。2015年是深化改革开放的关键年，国家重拳出击整治环境污染，推进长江经济带区域发展，故长江经济带各区域农业绿色生产效率变异系数趋于平稳。2017—2019年，长江经济带总体、上游、中游的变异系数在缓慢下降，说明“十三五”期间，长江经济带区域环境治理效果显著；在此期间，长江经济带上游、中游、下游农业绿色生产效率变异系数形成稳定态势，说明长江经济带上游、中游、下游采取的环境治理技术和治理措施形成了各自稳定的农业技术推广和传播状态。总体而言，长江经济带农业绿色生产效率变异系数最终稳定在0.26，上游农业绿色生产效率变异系数稳定在0.21，二者之间差距较小，表明长江经济带农业绿色生产效率总体与上游存在α收敛。下游农业绿色生产效率变异系数稳定在0.43，但中游变异系数却稳定在0.13以下，二者之间相差近2倍，故不存在α收敛，因此需要进一步进行β收敛分析。

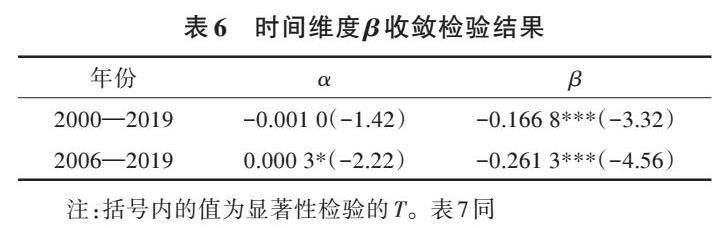
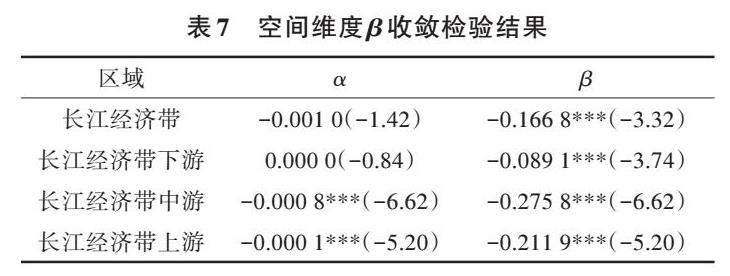
2.4.2 β收敛检验 采用面板固定效应模型相比于一般的回归模型更有利于控制不同地区在气候和自然资源环境等方面的差异，因此利用固定效应模型从时间维度和空间维度根据式（3）进行回归分析，结果如表6、表7所示。从时间维度（表6）可以看出，2000—2019年，β在1%水平显著为负。由α收敛分析可知，2000—2005年，长江经济带各省市农业绿色生产效率变异系数处于波动状态，因此该阶段不做β收敛分析。2006—2019年，β在1%水平显著为负，故2006—2019年长江经济带各省市农业绿色生产效率存在绝对β收敛。从空间维度（表7）可以看出，长江经济带无论是从整体上还是分区域上，β均在1%水平通过检验且全部为负，进一步验证了长江经济带各省市农业绿色生产效率存在绝对β收敛，且收敛状态稳定。两个维度检验结果均显示存在绝对β收敛，说明长江经济带区域农业绿色生产效率发展稳定，区域一体化建设卓有成效。从β绝对值看，长江经济带中上游β的绝对值远大于长江经济带下游，说明长江经济带中上游省市农业绿色生产效率远高于下游省市，下游省市农业绿色生产进入缓慢增长期。

3 小结与建议

3.1 小结

本研究分别运用面板三阶段DEA模型和面板固定效应模型对长江经济带农业绿色生产效率进行了实证测度及收敛性分析，得出以下结果。

第一，环境因素和随机误差对长江经济带农业绿色生产效率具有显著影响。农村实际可支配收入的提高有利于减少投入冗余，提高资源的利用效率，从而提高农业绿色生产效率；人口城镇化水平的提高有利于带动充分就业，减少劳动力冗余，但却造成严重的机械动力的浪费；产业结构高度化对污染环境的投入使用量有明显的降低作用，却会造成其他投入资源的浪费。

第二，从变异系数看，长江经济带上游、中游、下游的农业绿色生产效率存在区域不均衡现象。长江经济带农业绿色生产效率差异由小到大依次为中游、上游、下游。2017—2019年长江经济带三大区域农业绿色生产效率差异呈缩小趋势。

第三，从收敛结果看，长江经济带整体和上游地区农业绿色生产效率存在α收敛，而长江下游和中游地区则存在绝对β收敛。长江经济带中上游省市农业绿色生产效率远高于下游省市，下游省市农业绿色生产效率较低且增长缓慢。

3.2 建议

基于以上研究结论，为了从总体上进一步提高及从空间上优化长江经济带农业绿色生产效率，进而推动该区域农业朝着更高质量方向发展，提出以下对策建议。

第一，明确地区环境，因地制宜。多措并举提高农民收入，鼓励剩余劳动力转移，推动城镇化发展；同时引进新型农业技术，提高农业机械动力利用率；优化农村产业结构，加大环境污染治理力度，全方位提高资源利用率，促进农业绿色生产效率提高。

第二，把握区域差异，精准施策。长江经济带上游地区继续落实相关农业政策，稳步推动农业绿色生产效率提高；中游地区完善农业推广体系，向落后区域传播高效农业生产技术及方式；下游地区需要引进农业科技人才，释放科技创新潜能，提高农业绿色生产效率。

第三，打破区域壁垒，协同发展。加快市场体系建设，减少地区行政壁垒，畅通要素流动路径，推动各省市农业绿色生产率提高，缩小区域差距，实现长江经济带农业绿色生产效率区域联动和协同提高。

参考文献：

［1］ 王若梅，马海良，王 锦.基于水-土要素匹配视角的农业碳排放时空分异及影响因素——以长江经济带为例［J］.资源科学，2019，41（8）：1450-1461.

［2］ 王学婷，张俊飚.双碳战略目标下农业绿色低碳发展的基本路径与制度构建［J］.中国生态农业学报（中英文），2022，30（4）：516-526.

［3］ 张俊飚，何 可.“双碳”目标下的农业低碳发展研究：现状、误区与前瞻［J］.农业经济问题，2022（9）：35-46.

［4］ BRAVO-URETA B，PINHEIRO A. Efficiency analysis of developing country agriculture：A review of the frontier function literature［J］. Agricultural and resource economics review， 1993， 22（1）：88-101.

［5］ HELFAND S M， LEVINE E S. Farm size and the determinants of productive efficiency in the Brazilian Center-West［J］ . Agricultural economics， 2004， 31（2）：241-249.

［6］ MONCHUK D C.中国农业生产非效率的影响因素分析［J］.世界经济文汇，2009（2）：47-56，11.

［7］ 黄炎忠，罗小锋，李兆亮.我国农业绿色生产水平的时空差异及影响因素［J］.中国农业大学学报，2017，22（9）：183-190.

［8］ 郭海红，刘新民.中国农业绿色全要素生产率的时空分异及收敛性［J］.数量经济技术经济研究，2021，38（10）：65-84.

［9］ 李翠霞，许佳彬，王 洋.农业绿色生产社会化服务能提高农业绿色生产率吗［J］.农业技术经济，2021（9）：36-49.

［10］ 邓 波，张学军，郭军华.基于三阶段DEA模型的区域生态效率研究［J］.中国软科学，2011（1）：92-99.

［11］ 相天东.我国区域碳排放效率与全要素生产率研究——基于三阶段DEA模型［J］.经济经纬，2017，34（1）：20-25.

［12］ 郭四代，仝 梦，郭 杰，等.基于三阶段DEA模型的省际真实环境效率测度与影响因素分析［J］.中国人口·资源与环境，2018，28（3）：106-116.

［13］ 井 莉.环境规制下我国粮食生产绿色全要素生产率分析［J］.南方农业学报，2021，52（8）：2311-2318.

［14］ 刘亦文，欧阳莹，蔡宏宇.中国农业绿色全要素生产率测度及时空演化特征研究［J］.数量经济技术经济研究，2021，38（5）：39-56.

［15］ FRIED H O， LOVELL C A K， SCHMIDT S S， et al. Accounting for environmental effects and statistical noise in data envelopment analysis［J］. Journal of productivity analysis， 2002（17）： 121-136.

［16］ 刘自敏，张昕竹，杨 丹.我国省级政府卫生投入效率的时空演变——基于面板三阶段DEA模型的分析［J］.中央财经大学学报，2014（6）：97-104.

［17］ 罗登跃.三阶段DEA模型管理无效率估计注记［J］.统计研究，2012，29（4）：104-107.

［18］ 刘 艳.数字普惠金融对农业全要素生产率的影响［J］.统计与决策，2021，37（21）：123-126.

［19］ 肖 琴，周振亚，罗其友.长江经济带农业绿色生产效率及其时空分异特征研究［J］.中国农业资源与区划，2020，41（10）：15-24.

［20］ 李兆亮，罗小锋，薛龙飞，等.中国农业绿色生产效率的区域差异及其影响因素分析［J］.中国农业大学学报，2017，22（10）：203-212.

［21］ 吴传清，黄 成.排污异质性与长江经济带工业绿色转型发展研究［J］.湖北大学学报（哲学社会科学版），2021，48（1）：105-114，173.

［22］ 李 波，王春妤，张俊飚.中国农业净碳汇效率动态演进与空间溢出效应［J］.中国人口·资源与环境，2019，29（12）：68-76.

［23］ 张玉昌，宋 建.要素配置、产业发展与产业结构——基于政府主导的产业发展战略视角［J］.南方经济，2018（9）：86-106.

［24］ 程琳琳，张俊飚，何 可.空间视角下城镇化对农业碳生产率的直接作用与间接溢出效应研究［J］.中国农业资源与区划，2019，40（11）：48-56.

［25］ 沈 洋，周鹏飞.农业绿色全要素生产率测度及收敛性分析——基于碳汇和碳排放双重视角［J］.调研世界，2022（4）：58-68.

［26］ 李欠男，李谷成，尹朝静.中国农业绿色发展水平的地区差异及收敛性——基于地级市面板数据的实证［J］.中国农业大学学报，2022，27（2）：230-242.

收稿日期：2023-02-28

基金项目：湖北省教育厅哲学社会科学研究项目（19Q045）；长江大学社会科学基金项目（2017csza02）

作者简介：徐东芳（1996-），女，湖北咸宁人，在读硕士研究生，研究方向为农业经济管理及技术经济，（电话）15307248728（电子信箱）1306789028@qq.com；通信作者，孔令成（1987-），男，湖北仙桃人，讲师，博士，主要从事农业家庭经营与管理研究，（电话）18986661639（电子信箱）konglingcheng110@sina.com。