学科记忆育德的实践路径*

许天枢 朱加佳

【摘 要】学校教育要突出对学生道德品质与能力素养的培养。课堂教学应以学生的整体发展为目标，实施指向育人的教学实践。教师在学科教学过程中应充分挖掘学科的育人价值，将学科文化记忆与学生品德培养相结合，发挥学科的育人价值。

【关键词】记忆育德；学科育人；数学课堂；勾股定理

【中图分类号】G421  【文献标志码】A  【文章编号】1005-6009（2024）15-0022-04

【作者简介】1.许天枢，南京市宁海中学分校（南京，210036）校长，高级教师，江苏省数学特级教师；2.朱加佳，南京市第五十中学（南京，210003）教师，二级教师。

记忆作为客观事物在人脑海中留存的主观印象，建构于人对客观事物理解的基础上。记忆育德通过调用记忆的方式将已知事物再融合理解，挖掘其中的育德价值，并渗透进学科教学中。以数学学科为例，数学文化是数学学科学习中的独家记忆，不仅可以增强学生的学科文化素养，还可以激发学生的学习兴趣，增强学生的民族自豪感。数学教师在课堂教学中唤醒学生的学科记忆，可以激发学生的探究欲，丰富学生的情感体验，引导学生深入思考，进而形成正确的世界观、人生观和价值观。

勾股定理作为“千古第一定理”，是数学学科发展的里程碑，从数量关系到位置关系，联结了代数与几何。本文以“勾股定理”课堂教学为例，谈教师如何引导学生在“勾股定理”的发现与发展历程中感受数学文化，探索数学学科记忆育德的实践路径。

一、寻找记忆：在文化印记中发现数学

教师应在历史发展的进程与学科文化的传承中唤醒学生的学科记忆，寻找适配主题的记忆元素，构建记忆场，形成相关的记忆单元，为课堂教学的实施挖掘记忆素材，充分发挥记忆的育德作用。

教学导入阶段，教师可以出示图1，图2，图3。图1分别是2002年在北京举行的国际数学家大会与2021年在上海举行的国际数学教育大会的会徽，设计理念源于我国1800多年前三国时期赵爽的《周髀算经注》，该书记录了对勾股定理最早的证明。图2为“勾股圆方图”，这表明勾股定理是我国古人智慧的结晶。图3为1955年希腊发行的邮票，是毕达哥拉斯发现勾股定理的启发图案，故勾股定理在西方也被称为毕达哥拉斯定理。

图1国际数学大会会徽中的“赵爽弦图”“勾股圆方图”元素，昭示了其历史地位与重要性，说明中国文化受到了世界的重视。这使学生对本节课的主题研究产生敬畏之心，调动了学生主动学习与探究的积极性。

二、重构记忆：在现象观察中抽象数学

在寻找记忆过程中，学生形成了抽象的数学感知与数学印象，因此在数学文化中提炼数学问题就成为必然，通过问题思考与问题解决引导学生对现象本质的挖掘则是应然结果。教师可引导学生从现象观察出发，利用几何直观感受，猜想得出勾股定理的结论，培养学生严谨的思维品质。

教师要将“寻找记忆”中的数学元素转化为数学问题，引导学生探究其中关键数学元素之间的关系。如毕达哥拉斯受启发的图案中，抓住关键的数量关系——面积，并将其转化为方格纸上的探究，便于计算与得出结论。记忆重构中，教师引导学生从文化记忆中抽象出数学模型，充分研究它的数量关系，同时将学科的文化记忆融通形成自身的认知记忆。

例如，将图形关系探究特殊化为易于计算说理的等腰直角三角形的三边关系，以求得三边所作正方形的面积，奠定探究面积关系的研究思路（见图4）；在此基础上变式，形成一般图案的关系探究，在三边关系最为典型的[3、4、5]的直角三角形基础上开展自主探究（见图5）。这样既能引导学生利用面积法探索直角三角形的三边关系，又能够强化学生对[3、4、5]数据的感知，实现记忆的强化与深度建构。

三、再现记忆：在操作探究中理解数学

伴随记忆场域的构建，学生脑海中已经形成多个记忆模块，但缺少每个记忆模块之间的联系链条。为了将这些记忆模块形成整体，教师需要在原记忆的基础上进一步探究与追寻，让学生能够像数学家一样思考，在知识发现和知识应用中形成闭环。教师可通过记忆再现，增强学生对知识探索的自豪感，引发其对文化传承与发展的共鸣。

从数学文化现象到数学问题，从数学问题回到数学现象，教师在课堂教学过程中挖掘数学文化中的数学问题，引导学生开展探究活动。如“赵爽弦图”体现的勾股定理，教师可在几何关系中推理并证明，引导学生从不同角度思考，探索更多的证明方法。教师通过表格呈现直角三角形三边的规律，指导学生借助数学工具，如字母表示数、完全平方式等进行论证。例如，教师展示图6，图7，图8。图6为赵爽弦图的数学化表示，探究四个全等的直角三角形与两个正方形之间的面积关系；图7为毕达哥拉斯证明方法，是类似图6将四个全等的直角三角形翻了出去，找寻三角形与正方形之间的面积关系证得；图8为美国总统加菲尔德利用面积法证得，探究两个全等的直角三角形和一个直角三角形之间的关系。三种证明方法都是文化记忆的再现。

四、创新记忆：在问题解决中应用数学

《义务教育数学课程标准（2022年版）》提出，数学教育承载着立德树人的根本任务和实施素质教育的功能，其中最重要的一项是发展实践能力和创新精神，形成和发展核心素养，增强社会责任感，树立正确的世界观、人生观、价值观。在数学课堂学习中，教师通过记忆唤醒与重构，帮助学生形成对知识的初步理解与应用，但知识习得不是教育的最终目标，教师还要关注学生的情感发展与体验。

1.在问题中寻证明

经过严谨的论证过程与猜想之后，学生已经初步形成对勾股定理的认识与理解，将学科的文化记忆构建成为自己的认知与学科知识记忆。此时，教师可引入其他证明方法，引导学生感受数学知识探索过程的殊途同归，在数学的变化与创新中感知数学之美。

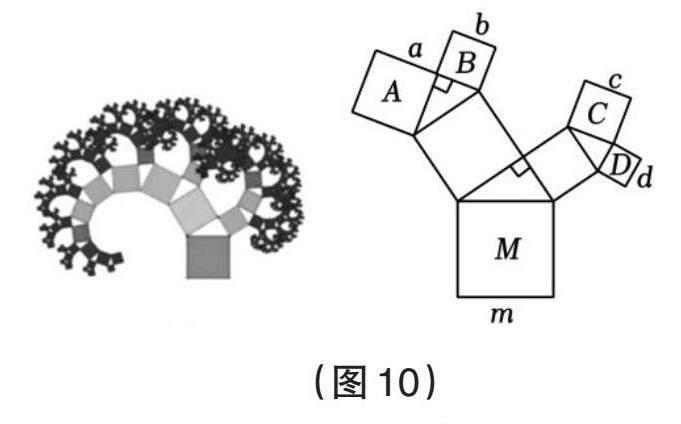
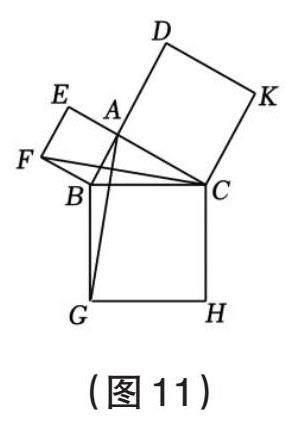
意大利著名画家达·芬奇证明了勾股定理（见图9），若设第一幅图中空白部分的面积为S1，第三幅图中空白部分的面积为S2，探索S1，S2与a，b，c的关系并利用达·芬奇的方法证明勾股定理。如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程后的形状好似一棵树，故被称为“勾股树”，这是毕达哥拉斯根据勾股定理画出来的，故被称为“毕达哥拉斯树”（见图10）。在“勾股树”的某部分图形中，设大正方形M的边长为定值m，四个小正方形A，B，C，D的边长分别为a，b，c，d，探究a，b，c，d，m之间的关系。欧几里得编纂的《几何原本》中也有证明勾股定理的方法，教师可借此图引导学生探究勾股定理（见图11）。

2.在问题中探应用

从文化到数学、从数学到生活，教师引导学生在解决问题中感受数学文化，以全新的视角思考文化记忆带动学科发展的过程。例如：教师让学生观察“赵爽弦图”的变化（见图12）。若将“赵爽弦图”的四个直角三角形中较长的直角边分别向外延长一倍，得到如图所示的“数学风车”，在Rt△ABC中，AC=m，BC=n，∠ACB=90°，求这个风车的外围周长（图中实线部分）。教师还可以引入数学文化的问题思考。如图13，明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地。送行二步恰竿齐，五尺板高离地。”翻译成现代文为：如图，秋千OA静止的时候，踏板离地高一尺（AC=1尺），将它往前推进两步（EB=10尺），此时踏板升高离地五尺（BD=5尺），求秋千绳索（OA或OB）的长度。

再如，教师可以引导学生探索生活情境问题，这既能提升学生的问题解决能力，又能潜移默化地引导学生形成新的文化记忆理解。如图14，消防云梯主要是用于高层建筑火灾等救援任务，它能让消防员快速到达高层建筑的火灾现场，执行灭火、疏散等救援任务。消防云梯的使用可以大幅提高消防救援的效率，缩短救援时间，降低救援难度和风险。如图，已知云梯最多只能伸长到50米（即AA'=BB'=50米），消防车高3.4米，救人时云梯伸长至最长，在完成从33.4米（即A'M=33.4米）高的A处救人后，还要从51.4米（即B'M=51.4米）高的B处救人，这时消防车从A处向着火的楼房靠近的距离AB为多少米？

总之，记忆育德建立在学科文化记忆的背景下，通过学科文化记忆的唤醒、重构、创新，促进学生问题解决能力的提升和学科文化素养的发展，充分发挥记忆的德育价值，拓宽了学科德育的途径。

【参考文献】

［1］ 张大均.教育心理学［M］.北京：人民教育出版社， 2011.

［2］ 张维忠，唐慧荣.中国古代数学的图腾：赵爽弦图［J］.中学数学月刊， 2023（6）：1-3.

［3］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社， 2022.