创设有效问题 引领数学探究

陈燕

［摘  要］ 在研究双曲线的定义及其标准方程的过程中，教师应将研究的主动权交给学生，通过创设有效的问题情境引领学生经历动手实验、自主探究、合作交流等活动，以此充分体验数学研究的乐趣，促进探究性学习和深度学习的真正发生，有效提高课堂教学有效性.

［关键词］ 类比；探究性学习；深度学习

双曲线是高中数学的重要内容之一，双曲线的定义及其标准方程更是重中之重. 若教学中直接呈现定义及标准方程让学生理解和记忆，则难以引发深度学习，不利于学生学习能力的提升. 因此，在日常教学中，教师应结合教学实际创设有效问题，让学生在问题的驱动下主动参与定义及标准方程形成的过程，以此深化学生对知识的理解，提高学生的学习能力及数学素养.

教学分析

双曲线是继椭圆后又一重要的圆锥曲线，它在生活中有重要的应用价值. 在研究双曲线之前，学生研究过椭圆，两者既有联系又有区别，因此教学中应有意识地引导学生进行新旧知识的类比，让学生将椭圆的学习经验顺利地迁移到双曲线中，以此增强学生的自主学习意识，提升学生的数学素养.

高中生虽然具备一定的空间想象、数学抽象、逻辑推理等素养，但是面对抽象的定义和性质时依然会产生畏难情绪，因此教学中应提供更多机会让学生去实验、去观察、去类比，以此通过多感官的协同发展促成探究性学习、深度学习，提高课堂教学有效性.

教学过程

1. 新旧联系，有的放矢

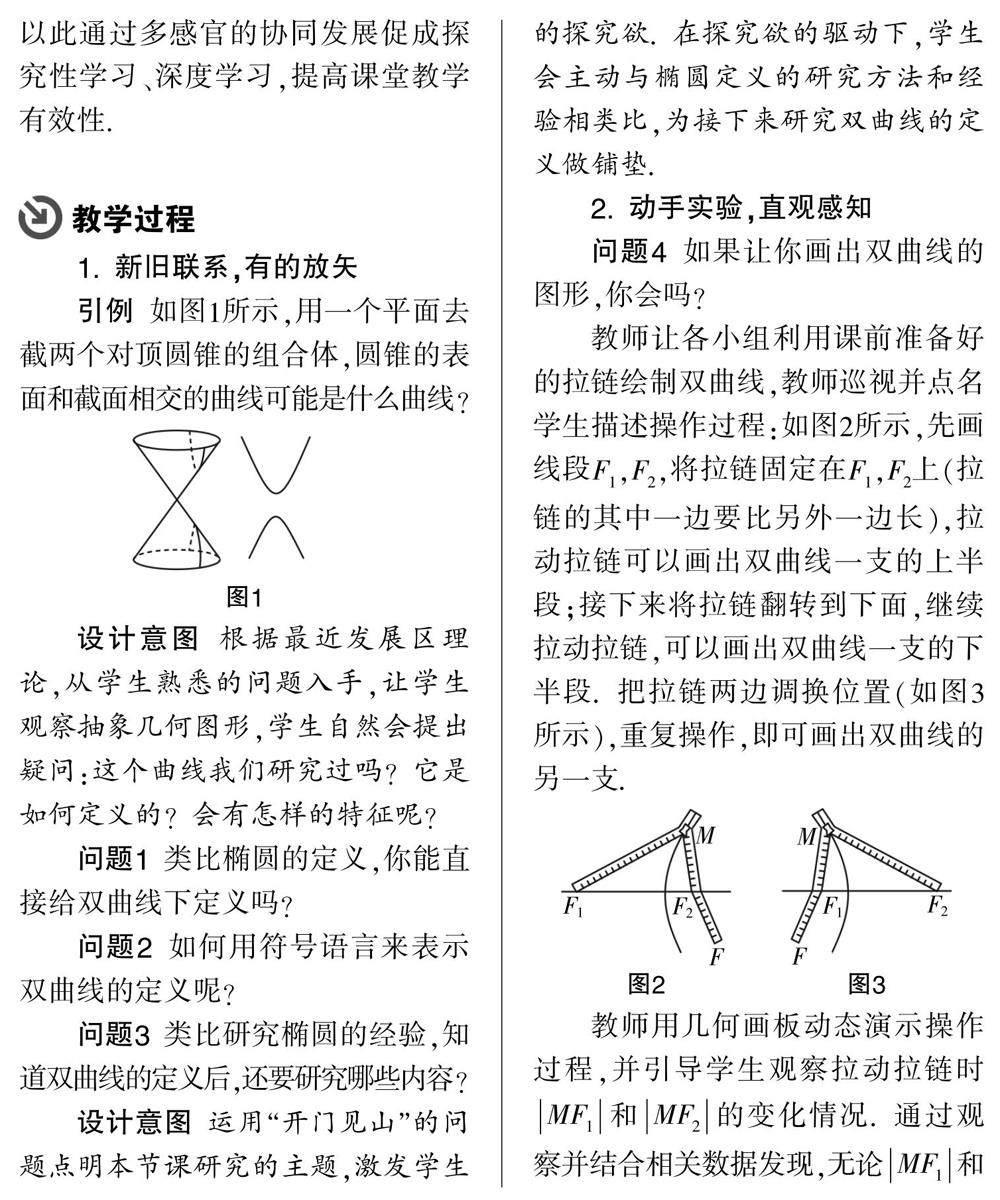
引例 如图1所示，用一个平面去截两个对顶圆锥的组合体，圆锥的表面和截面相交的曲线可能是什么曲线？

设计意图 根据最近发展区理论，从学生熟悉的问题入手，让学生观察抽象几何图形，学生自然会提出疑问：这个曲线我们研究过吗？它是如何定义的？会有怎样的特征呢？

问题1 类比椭圆的定义，你能直接给双曲线下定义吗？

问题2 如何用符号语言来表示双曲线的定义呢？

问题3 类比研究椭圆的经验，知道双曲线的定义后，还要研究哪些内容？

设计意图 运用“开门见山”的问题点明本节课研究的主题，激发学生的探究欲. 在探究欲的驱动下，学生会主动与椭圆定义的研究方法和经验相类比，为接下来研究双曲线的定义做铺垫.

2. 动手实验，直观感知

问题4 如果让你画出双曲线的图形，你会吗？

3. 数学建构，解锁方程

问题5 如何求双曲线的标准方程呢？

师生先共同回顾椭圆的标准方程的推导过程，然后预留时间让学生自行推导双曲线的标准方程，教师巡视指导.

设计意图 学生已经理解并掌握了椭圆的标准方程的推导过程，且具有一定的逻辑推理和数学运算能力，因此教师放手让学生独立推导双曲线的标准方程，以此提高学生的逻辑推理能力，训练学生的数学运算能力，提升学生的数学素养.

经过几分钟思考与探究后，大多数学生已经完成了双曲线的标准方程的推导，教师鼓励学生提出自己在推导过程中遇到的问题.

生1：两次平方后整理得到（a2－c2）x2+a2y2=a2（a2－c2），感觉有点不太对，怎么和椭圆的方程一样呢？难道是我运算出错了？

师：大家真的太棒了. 结合双曲线与椭圆的相同点和不同点，得到了双曲线的标准方程. 类比椭圆的标准方程可知，双曲线的标准方程也分为焦点在x轴上和焦点在y轴上两种，那么焦点在y轴上的双曲线的标准方程又会是什么呢？

设计意图 呈现学生的思维过程，通过有效的启发和引导，帮助学生排疑解惑. 学生推导焦点在x轴上的双曲线的标准方程后，教师引导他们对比分析，发现焦点在y轴上的双曲线的标准方程.

4. 知识应用，深化理解

例1 以下方程是双曲线吗？如果是，请指出a，b，c的值及焦点的坐标.

设计意图 通过具体练习引导学生思考辨析，进一步强化学生对双曲线的概念及其标准方程的理解与记忆.

例2 已知双曲线的焦点坐标分别为（－3，0），（3，0），双曲线上一点P到两焦点的距离差的绝对值为4，求双曲线的标准方程.

设计意图 通过适度练习达到巩固“双基”的目的，同时通过变式训练揭示问题的本质，提高学生的学习品质，增强学生的解题信心.

5. 反思提炼，升华认知

问题6 回顾探究过程，你有哪些收获？

设计意图 预留时间让学生回顾反思，归纳总结本节课学习了哪些知识，掌握了哪些方法，还有哪些困惑，通过深度交流进一步了解学生所思、所想、所惑，为针对性练习提供依据，促进“减负增效”的落实.

教学思考

1. 贯彻“以生为本”教学理念，引导自主探究

课堂教学的主体是学生，因此课堂教学应贯彻“以生为本”教学理念，从学生的认知水平出发，设计符合学生实际学情的教学活动，以此来提高学生的学习能力，提升学生的数学素养. 在本节课教学中，教师为学生营造了一个和谐、平等的学习氛围，通过适时的启发和点拨，引导学生积极思考、主动探究. 在这样的情境下学习，学生的思维是活跃的，课堂氛围是愉悦的，有利于学生的学习能力和思维能力的发展与提升.

2. 关注数学思想，引发深度学习

在本节课的探索过程中，教师引导学生类比椭圆相关内容，这样既促进旧知的巩固，又为新知的探究指明了方向. 类比思想是数学中的重要思想方法，教学中教师要有意识地引导学生对相关或相似内容进行类比，以此通过对相同点与不同点的深度探究，逐渐形成观察发现、积极思考的习惯，提升学生的数学素养.

3. 合理设计问题，发展數学思维

在本节课教学中，教师没有直接将内容呈现给学生，而是以学生的认知水平为出发点，精心设计问题，让学生在问题的驱动下积极思考、主动操作、积极交流，以此启迪学生的思维，激发学生的探究欲. 同时，通过问题的解决加深学生对双曲线本质的理解，提高学生分析和解决问题的能力. 在教学中，教师应认真研究学生，了解学生的实际学情，以便通过最近发展区问题的设置来引发深度学习，提高教学的有效性.

4. 鼓励合作学习，培养合作意识

动手实践、自主探究与合作交流是数学学习的重要形式. 在教学中，教师要为学生营造合作氛围，培养学生主动获取知识的能力和创新思维. 在本节课教学中，教师让学生以小组为单位绘制双曲线，自主设计实验方案与策略，为学生营造了良好的合作氛围，提高了课堂教学效率.

总之，在数学教学中，教师不能大包大揽，而应多提供一些机会给学生自主探究与合作交流，以此通过学习形式的多样化来调动学生参与课堂的积极性，提高课堂教学的有效性.