基于动态交通的电动车路径选择

唐松涛 王皓

摘要 电动车因绿色环保和出行费用低等特点，日益成为重要代步工具，但电动车的续航能力有限制约了车辆的使用效率和行驶范围。因此，根据道路信息、用户需求及车辆条件，选择合理路径降低出行成本成为亟待解决的问题。文章先采用元胞传输模型和交通基本图预测道路行程时间，随后结合车辆能耗和充电过程构建路径选择模型；然后，利用遗传算法求解该模型；最后，通过实验验证电动车路径选择模型的可行性。实验结果表明：相较于静态路网，模型可帮助电动车提高5.9%续航里程，减少34.3%行程时间。另外，该模型可适应用户不同需求下的路径选择。

关键词 交通经济；交通规划；路径选择；交通预测；动态交通；电动车

中图分类号 U461.99文献标识码 A文章编号 2096-8949（2024）06-0028-04

0 引言

电动车凭借其绿色高效的优势，成为日常出行的主要工具。如何在有限的技术条件下使电动车低成本、高效地出行，一直是国内外各界广泛关注的问题。

出行者的出行成本与电动车路径选择有关。电动车路径选择问题本质上是车辆路径规划问题在新场景中的延续[1]。车辆内部因素主要为车辆充电需求、车辆车型、车辆电池容量等方面。其中，Desaulniers G[2]等在研究带时间窗电动车辆路径选择问题时，构建了多种充电路径及策略；Afroditi A [3]等考虑多种内部因素，包括车辆载重、车辆充电方式和电池电量等作为约束，构建电动车路径选择模型。同时，外部环境因素如路况同样也会影响车辆的续航里程，因此，外部环境因素也有考虑的必要。

车辆外部影响主要来自路网中的交通因素，包括但不限于道路等级、道路线形及交通条件等方面。其中，张建寰[4]分析了交通路况对电动汽车的影响，并构建了基于静态交通路况信息的行程距离最短的电动汽车路径选择模型。邢强[5]等采用动态的交通路网信息，建立了路网的路阻模型，同时构建了基于电动车的多目标路径选择模型。Yang H[6]等同时分析了交通信息和充电价格的影响，构建了多目标的电动车路径优化模型。但是，上述研究并未兼顾内外因素。

在以上研究的基础上，该研究同时考虑了预测的动态交通信息和车辆内外部因素，分析了路况对能耗的影响，结合用户的不同需求构建了电动车最低广义出行成本路径选择模型，并采用遗传算法对其进行求解。该研究的成果可进一步用于电动车的导航、交通诱导和充电站选址等相关研究，为其提供参考依据。

1 路网信息预测

该文采用续航里程和行程时间来描述车况和路况，其中，续航里程的预测方法是基于速度的能耗模型，同时，行程时间的预测方法是基于元胞传输模型和交通基本图。

1.1 车况预测的影响因素

电动车续航里程的研究本质上是受到电池容量和能量消耗的共同影响。其中，影响电动车能耗的因素既有车辆电池放电效率、放电可循环次数、工作温度等这些车辆内部因素，还有行驶速度、道路坡度、道路等级等外部道路环境因素，且电动车能耗的变化过程是非线性的。

该文分析的重点是路况变化带来的车况变化，因此，行驶速度是评价车况的一个关键指标，同时，行驶速度在道路模型中也可获得。综上所述，行驶速度是构建能耗模型的关键变量。

1.2 基于速度的能耗模型

按照1.1小节的假设和分析，车辆续航里程可由电动车能耗直接决定。另外，该文研究重点之一是分析路况对车辆能耗的影响，因此，能耗模型变量是车况和路况中共有的变量。综上所述，从宏观角度说，车流的区间平均速度可以作为能耗模型的变量。

速度是通过驱动力实现对能耗的影响的。驱动力能克服阻力和提高加速度，而驱动力的能量来源便是电池的电能。速度与驱动力的数学关系公式（1）所示：

（1）

式中，Fv——电动车辆行驶的驱动力；m——电动汽车的总质量；f——电动汽车的滚动阻力系数；λ——旋转质量的换算系数；ρa——空气的密度，一般取1.225 8 km/m3；Cd——空气阻力数；Aw——迎风面积；v——车速。在驱动力作用下电动车的总能耗见公式（2）：

（2）

式中，Ev——电动车的总能耗（kW/h）；Δt——速度的统计周期。结合公式（1）和（2），速度与能耗数学关系见公式（3）：

（3）

1.3 路网建模

该文对路网进行了元胞划分。根据元胞划分的结果，该文采用加权图G（V，E，W）来表示道路网络的拓扑结构。其中，V为图中节点i的集合，结合元胞节点i表示对应的元胞i；E为图中边eij的集合，边eij表示元胞i和元胞j的连接关系；W表示节点权值wi的集合，wi权值为对应元胞的行程时间，能耗和是否包含充电站。

1.4 交通基本图和元胞传输模型

该文采用元胞传输模型对路况进行预测。元胞传输模型是动态离散地反映流量与密度的关系，可以有效地预测未来时刻的交通密度。在元胞传输模型（CTM）中[7]，单一元胞的主要变量如图1所示。

元胞传输模型的数学形式如公式（4）所示：

式中，ρi（t）——元胞i的密度；ri（t）——周期t内接收的总车辆数目；si（t）——周期t内发送的车辆数目，Li——元胞的长度。另外，ri（t）和si（t）的具体形式见公式（5）：

式中，vf ——自由流速度；Ci（t）——元胞i在周期t的通行能力；w——停车波的波速；ρim——元胞i的最大密度。

2 路径选择

基于廣义出行成本最低条件下的路径选择问题，可以描述为在电量和路径约束前提下的时间及能耗优化问题，并用遗传算法进行求解。

2.1 遗传算法

该文针对路径选择问题，设计了遗传算法的染色体，适应度函数，选择、交叉及变异的具体规则，及终止条件。适应度函数F的数学表示如公式（6）所示：

2.2 广义出行成本分析

交通出行成本是研究出行者出行决策行为的基础指标，考虑多因素影响的广义出行成本是目前出行成本研究的趋势[8]。该文针对不同预测信息和不同出行目标两类模拟结论，建立广义出行成本评价公式。出行者广义出行成本的基本表达式为：

C=c1+c2+c3 （7）

式中，C——广义出行成本；c1——行程时间成本；c2——等待时间成本；c3——充电时间成本。广义出行成本测算模型为：

式中，V——出行者单位时间价值，根据经验[8]，V的推荐值计算方式如下：

式中，β——小时工资率（元/h）。该文β取值为13.91。

3 实例应用

3.1 算例设置

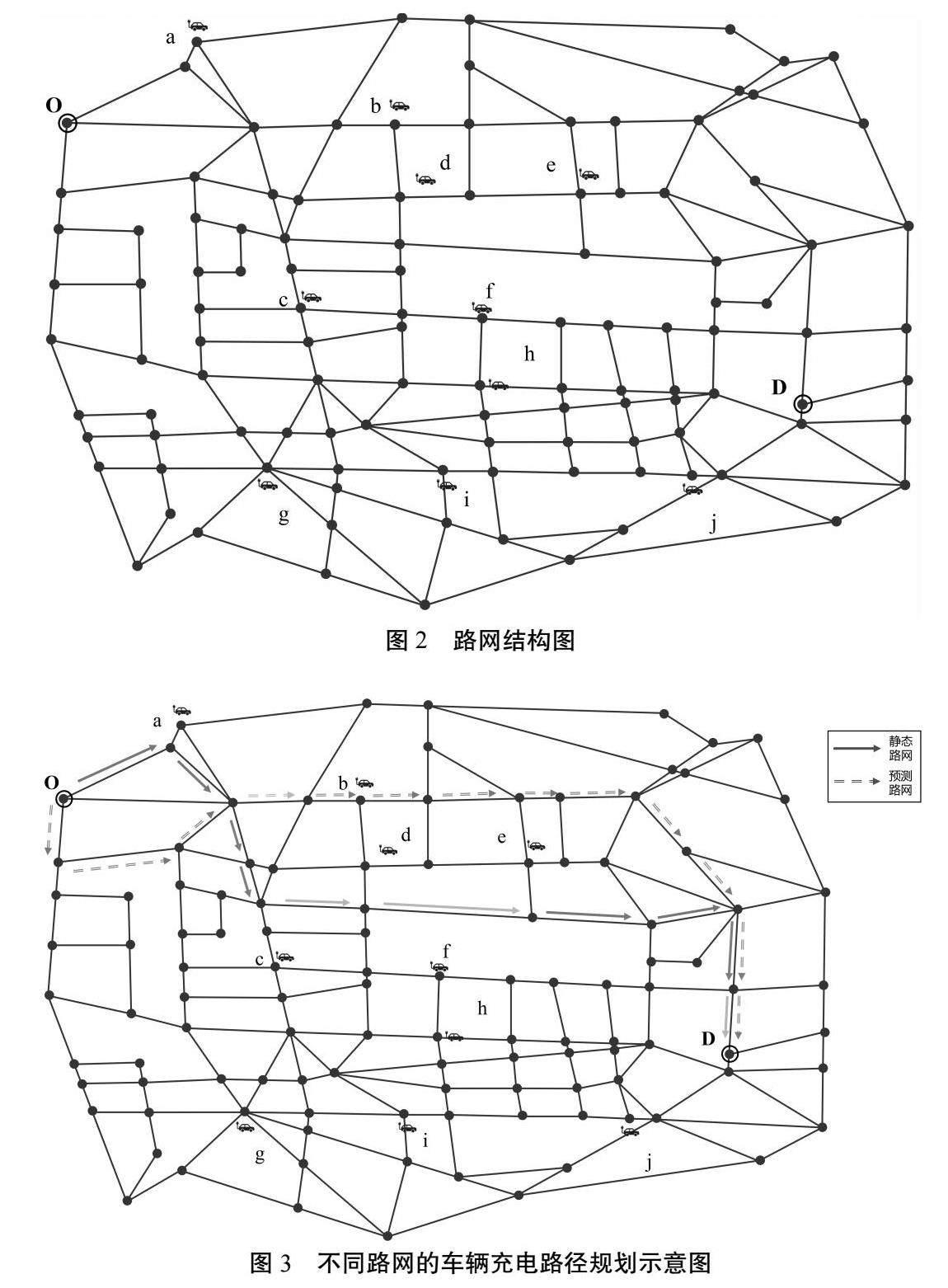
该文选取了一个包含114个节点的交通路网来验证电动车路径选择方法的可行性，其中，10个节点包含充电站。路网为北京市30 km×30 km的实际路网，结合调查的结果获取充电站的信息，路网结构如图2所示，其中，充电站位置节点的数量、充电功率等参数如表1所示。

3.2 路径选择分析

3.2.1 预测信息对路径选择的影响

该文分别设置电动汽车在静态路网和预测路网中进行路径选择的信息，其中静态路网的路况信息为出发时的采集信息，而预测路网中，路况信息为基于元胞传输模型和基本图预测获得的。

出发时间设置为下午18：10，初始电量为电池容量的60%，且起讫点不变。设置车辆随机到达，到达车辆数服从泊松分布。在两种情形下求得出行路径如图3所示，图中箭头从绿到红表示续航里程依次递减，两种场景的指标如表2所示。

从实验结果可见：静态路网的路况信息的广义出行成本低于预测路网，且总行程时间大于预测路网，续航里程仅略高于预测路网。从静态路网行驶过程的续航里程变化来看，静态路网是通过牺牲速度来实现的，同时，在没有充电的情况下静态路网广义出行成本低于预测路网，考虑静态路网并未精准预测等待時间和充电时间，静态路网在路网中的行驶时间理论上更长，因此，预测的路况信息有助于降低行程时间，从而降低运输成本。

3.2.2 不同出行目标下的充电路径分析

根据电动汽车用户的个性化需求，在动态路网中设置不同的参数σL、σT从而得到三种不同目标下的电动汽车充电规划路径，目标参数的设置如表3所示。

这三种不同情况下需要保证除了目标函数不同之外，其他的参数都要保持一致，并与上文实验相同。实验结果如图4所示，量化指标结果如表4所示。

图4中不同需求的具体路径可见：行程时间最优往往会压缩充电时间甚至放弃充电来降低总的行程时间；而续航里程最优会尽可能地保证电量充足，并不会一味地寻找充电站，因为寻找充电站会增加电量的消耗。因此，在这种情况下，模型仍可以权衡电量的消耗。广义出行成本最优的路径相较前两者并没有太明显的特征。另外，三种情况下，在接近终点时，往往是通过牺牲速度来保存电量，而不是另寻充电站，猜测这与模型的约束有关。

参考表4中广义出行成本，由不同需求下的路径选择结果可知：以续航里程为需求的情况获得的路径续航里程最长，以行程时间最短为需求的情况下获得的路径行程时间最短，但三种目标下的各指标差距并不大，并不会因为需求不同带来指标上的明显差距，说明路况是影响路径选择的主要因素。

4 结束语

该文采用元胞传输模型和交通基本图结合路网拓扑，对动态交通进行预测，采用预测路网信息，在充分考虑车辆的能耗、行程时间和路径范围的情况下构建基于广义出行成本最低的多需求路径选择模型，并利用遗传算法对路径选择模型进行求解。为证明模型可行性，该文选取了续航里程、行程时间两个主要指标及其子指标，结合标准案例进行验证。实验结果表明：相较采用静态路网信息，采用预测的动态路网信息进行路径选择时，可以帮助电动车提高5.9%的续航里程和34.3%的行程时间，同时，间接证明预测的路况信息有助于降低运输成本。在允许充电的情况下，通过比较广义出行成本可知：车辆的行程时间和续航里程之间是两个相互矛盾优化目标，车辆无法同时保证续航里程和行程时间同时达到最优，其中，相同道路条件下充电时间和等待时间会带来额外延误，但在综合两者优化目标的前提下，模型可以协调用户需求获得广义出行成本最优的路径。综上所述，该文研究可以帮助电动车提高行驶效率，降低出行成本。

参考文献

[1]赵志学， 李夏苗. 时变交通下生鲜配送电动车辆路径优化方法[J]. 交通运输系统工程与信息， 2020（5）： 218-225+239.

[2]Desaulniers G ， Errico F ， Irnich S ， et al. Exact algorithms for electric vehicle- routing problems with time windows[J]. Operations Research， 2016（6）： 1388-1405.

[3]Afroditi A ， Boile M ， Theofanis S ， et al. Electric vehicle routing problem with industry constraints： Trends and insights for future research [J]. Transportation Research Procedia， 2014（3）： 452-459.

[4]张建寰， 南洋. 基于交通信息影响下的电动汽车充电路径规划[J]. 计算机应用， 2016（S2）： 282-285.

[5]邢强， 陈中， 冷钊莹， 等. 基于实时交通信息的电动汽车路径规划和充电导航策略[J]. 中国电机工程学报， 2020（2）： 534-550.

[6]Yang H， Deng Y， Qiu J， et al. Electric Vehicle Route Selection and Charging Navigation Strategy Based on Crowd Sensing [J]. IEEE Transactions on Industrial Informatics， 2017（5）： 2214-2226.

[7]Daganzo C F. The cell transmission model part II： Network traffic [J]. Transportation Research Part B： Methodological， 1995， 29： 79-93.

[8]胡盼， 杨晓光. 基于广义出行成本的出行方案优化[J]. 系统工程理论与实践， 2017（4）： 982-989.