基于MATLAB的赖特函数分区算法研究及实现

李燕 袁晓

收稿日期：2023-08-28

DOI：10.19850/j.cnki.2096-4706.2024.05.001

摘  要：物理数学中的多数特殊函数可将复平面划分区域采用不同数值技术来计算。赖特函数在分数微积分及其工程应用中有着重要作用，作为一类新型特殊函数也可使用分区算法进行数值计算。通过研究赖特函数在大参数下的渐近展开式和公式中系数的计算方法，修正积分表达式及积分半径选择定理的错误，进一步改进完善复数域赖特函数的分区算法，并利用MATLAB软件进行编程仿真分析算法精度。实验结果表明，分区算法的适用性广，有良好逼近效果。

关键词：分数微积分；特殊函数；渐近展开；分区算法；MATLAB

中图分类号：TP301.6  文献标识码：A  文章编号：2096-4706（2024）05-0001-06

Research and Implementation of the Partitioning Algorithm for the Wright Function Based on MATLAB

LI Yan， YUAN Xiao

（College of Electronics and Information Engineering， Sichuan University， Chengdu  610065， China）

Abstract： Most special functions in physical mathematics can be calculated by dividing the complex plane into different regions and using various numerical techniques. The Wright function plays an important role in fractional calculus and its engineering applications. And as a new type of special function， the Wright function can also be calculated using the partitioning algorithm. By studying the asymptotic expansion of the Wright function under large parameters and the calculation method of coefficients in the formula， correcting the errors in the integral expression and the integral radius selection theorem， the partitioning algorithm of the Wright function in the complex field has been further improved and perfected， and finally MATLAB software is used for programming simulation to analyze the accuracy of the algorithm. The experimental results show that the partitioning algorithm has wide applicability and good approximation effect.

Keywords： fractional calculus; special function; asymptotic expansion; partitioning algorithm; MATLAB

0  引  言

指數函数  常出现在整数阶常微分方程与偏微分方程的解析中，在应用数学及概率论中有着核心作用。与经典微积分理论相似，新型特殊函数米塔-列夫勒函数[1-3]与赖特函数等在分数微积分中扮演着类似指数函数的角色，它们都是指数函数的推广，并继承了指数函数的一些显著特性。

1933年，Wright在研究分区渐近理论[4]时首次提出参数α＞0的赖特函数。1935年，Wright在研究广义超几何函数的渐近行为[5]时引入了福克斯-赖特函数，其定义为：

（1）

在同一论文中，他还研究了α＞0，γ＞0时的四参数赖特函数：

（2）

1940年，Wright在论文中[6]从数学角度再次研究了赖特函数Wα， β （z），并将参数α的范围扩展到α＞-1的实数域，故赖特函数的完整定义为：

（3）

赖特函数Wα， β （z）根据α的不同取值分为两种类型，分别为α＞0时的第一类赖特函数和-1＜α＜0时的第二类赖特函数。

随着分数微积分理论体系的完善和拓展，赖特函数的研究涵盖了不同领域，包括理论物理学[7，8]、概率论[9]等。在信号处理方面，赖特函数作为新型分数阶微积分初等函数之一，它的导数可以处理不完全可微和高阶可微信号，例如：在语音识别、图像识别和模式识别领域常常需要处理复杂信号，利用赖特函数可以提高信号处理精度。此外，机器学习也逐渐成为该函数应用的一个热门领域。科学家使用神经网络等技术来预测与分析数据中存在的整体行为和趋势，并且使用赖特函数作为一个强大工具来解决这些问题。赖特函数的应用日益增加，研究其性质及数值算法十分重要。

赖特函数的数值算法研究目前还处在一个探索阶段。2008年，Luchko提出了分区算法[10]，将实数域分成三个区域利用不同数值技术来计算具有实参数的赖特函数，但这种算法的积分表达式及积分半径选择定理存在问题。2010年，他修正了该算法的积分半径选择定理中的错误，可该算法只被限制在负实数域[11]上，同时缺少对大参数下赖特函数的渐近级数的研究，只能作为赖特函数数值计算的参考。本文是在Luchko的分区算法基础上，进一步研究赖特函数的渐近展开，详细论述了其渐近展开公式中系数的计算方法，同时对积分表达式中的错误进行修改并推广至复数域赖特函数的积分计算，最后利用MATLAB编写代码分析算法精度。

1  赖特函数的渐近展开

1940年，Wright首次利用应用于积分表示的最速下降法研究赖特函数的渐近展开性质[6]，但并未考虑到斯托克斯现象。1999年，赵育求等人研究得到赖特函数Wα， β （z）的渐近公式[12，13]，并研究了斯托克斯现象，但不全面。2010年，Paris研究了福克斯-赖特函数  的渐近展开[14]并在2014年的研究中考虑到该函数的斯托克斯现象[15]。2020年，Paris针对赖特函数的z参数取绝对值很大的实数及β取很大值的情况，建立了新的辅助函数研究其渐近展开[16]。2021年，Paris等人研究得到了两个赖特型辅助函数Fv （z）和Mv （z）（即Mainardi函数）的渐近展开[17]。

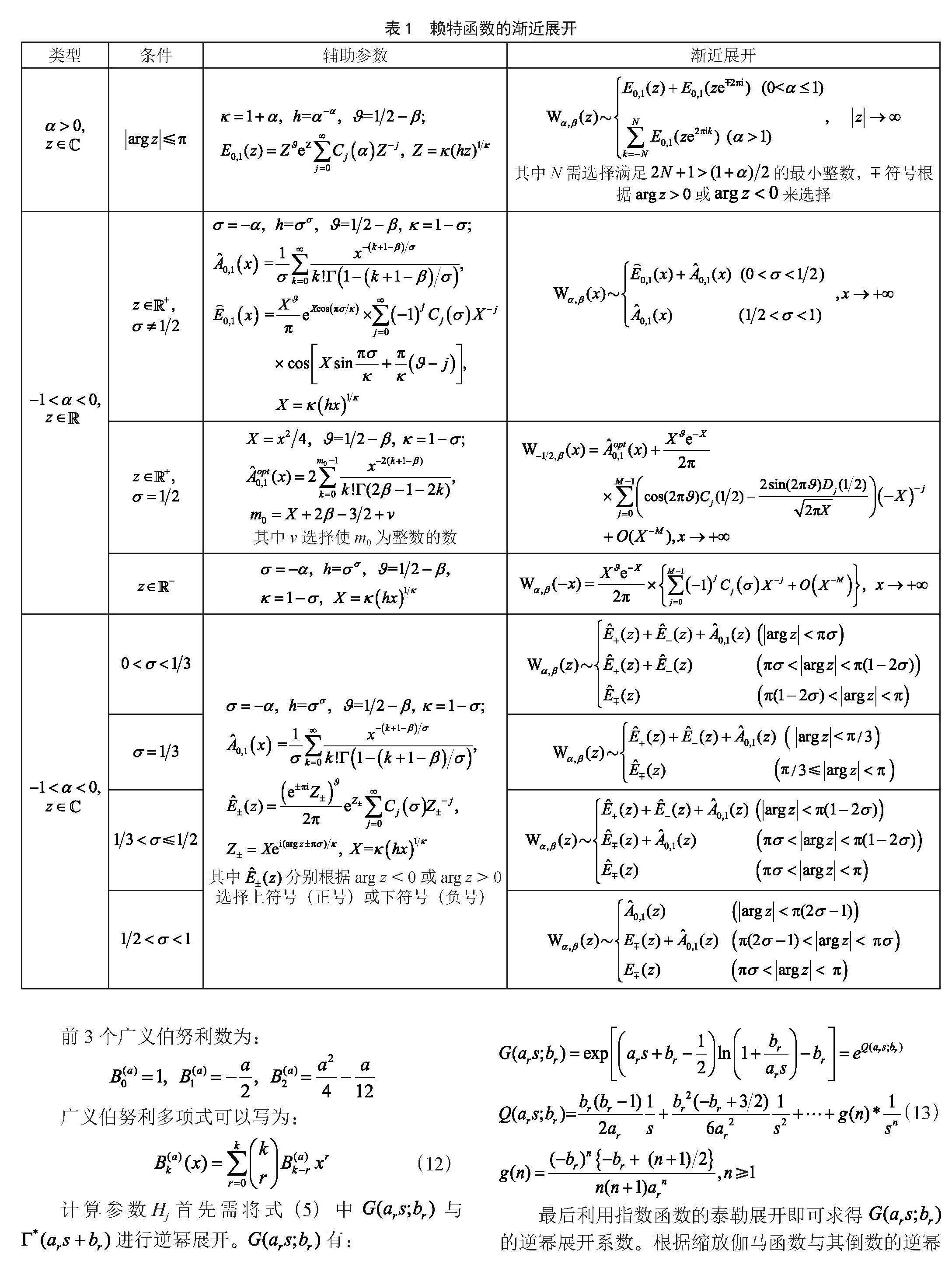
第一类赖特函數的渐近展开可直接利用文献[15]中福克斯-赖特函数  的渐近展开原理得到。参数-1＜α＜0的赖特函数的渐近展开不能直接采用  的渐近理论结果，需利用伽马函数的反射公式来求得。表1列举出赖特函数的渐近展开公式，其中系数Cj和Dj的计算将在第2节详细描述。

2  渐近展开中系数计算方法

2.1  系数Cj的计算方法

赖特函数渐近展开式中的系数Cj可依据超几何函数  渐近公式的系数计算方法[14]来确定。系数Cj出现g（s） / s！的逆阶乘展开式中，归一化系cj = Cj /C0根据该展开式可改写为：

（4）

其中 。将缩放伽马函数[18]中z替换为αs + β得到：

（5）

将式（4）左边式子利用式（5）通过一些常规代换可以写为

（6）

根据式（4）与（6）可以得到：

（7）

将式（7）左侧的乘积写成  的逆幂展开：

（8）

因为  存在展开[19]：

（9）

故式（7）的右侧式子随着  可化为：

（10）

对比式（8）和（10），可发现当1≤j≤M-1时有Hj = Xj，于是有：

（11）

式（11）为归一化系数cj的计算公式，主要需要计算参数Hj与  的值。其中  是广义伯努利多项式[20]。广义伯努利数定义为 ，可以由递推关系给出：

前3个广义伯努利数为：

广义伯努利多项式可以写为：

（12）

计算参数Hj首先需将式（5）中  与 进行逆幂展开。 有：

（13）

最后利用指数函数的泰勒展开即可求得  的逆幂展开系数。根据缩放伽马函数与其倒数的逆幂展开式[21]可以得到  与  的逆幂展开：

其中γk为斯特林系数[22，23]，可利用递推关系精确求出。

赖特函数的渐近展开会用到p = 0，q = 1和p = 1，q = 0两种情况，分别有：

其中σ = -α，δ = 1-β。两种情况的算法原理及编程相似，现针对p = 0，q = 1进行具体描述：

Y0， 1（s）的系数可以利用MATLAB中conv函数算出。

y011=conv（gammaxi（alf，bet，n1，2），gammaxi（1，1，n1，2））;%gammaxi（alf，bet，n1，2）计算  的系数；

%gammaxi（1，1，n1，2）计算  的系数；

y01=conv（y011，gammaxi（k，q1，n1，1））;%gammaxi（k，q1，n1，1）计算  的系数；

R0， 1（s）可以写为：

R0， 1（s）的系数可以利用MATLAB中symsum函数与taylor函数算出：

Q=symsum（（-1）^ii/（ii*（ii+1））*（q1^ii*（-q1+（ii+1）/2）/k^ii-b^ii*（-b+（ii+1）/2）/a^ii-（ii-1）/2）*（s）^ii，ii，1，n1）;

R011=exp（Q）;

R01=taylor（R011，s，'Order'，n1）;

R01=sym2poly（R01）;

将Y0， 1（s）与R0， 1（s）的系数进行卷积，即可得到Hj的值。

2.2  系数Dj的计算方法

赖特函数的渐近展开主要研究σ = 1/2（μ = 1）的情况，根据文献[15]可得到：

（14）

由式（14）可看出，系数Dj主要需计算Gk， j（1/2）参数。Gk， j（1/2）出现在展开式：

（15）

其中λ j = v - j，v = m0 - X - 2β + 3/2，v选择使m0为整数的最小数，X = x2/2。

对式（15）中  映射进行级数反演时，有：

（16）

更高系数g （k）可利用Mathematic软件中的InverseSeries函数获得。根据式（16）有：

（17）

利用式（15）与（17）进行系数卷积即可求得Gk， j（1/2）的值，更高系数可利用MATLAB求得。

GA1=（1+RT）^RJ;%GA1为 ；

GA=taylor（GA1，m，'Order'，n1）;%对  进行泰勒展开；

GA1=sym2poly（GA）;%获得多项式系数；

GG=conv（GA1，CRT1）;%CRT1为  的幂展开系数，两者卷积即可求得  的相反数；

3  分区算法

将复平面分为三个区域：A）| z |≤q1，0＜q1＜1，B）q1＜| z |≤q2，C）| z |＞q2，分别使用泰勒级数、积分表达式及渐近展开式来计算赖特函数。其中渐近展开在第1～2节已做具体论述，但无法从理论上预测评估精度。

3.1  泰勒级数

首先考虑A区域| z |≤q1，采用泰勒级数进行计算。

定理3.1，当| z |≤q1，0＜q1＜1，对于规定精度ε＞0有：

（18）

其中截断点满足：

3.2  积分表达

在区域B中，采用赖特函数的积分表达式定理3.1进行计算。被积函数  在积分区间上有界且积分区间也有界，故积分是有限的，可以直接通过MATLAB中integral函数以规定的精度ε＞0来计算。被积函数K涉及无穷上限，需对积分半径进行截断，得到积分半径选择定理3.2。

定理3.1一般情况下，赖特函数Wα， β （z）的积分表达式为：

（19）

当-1＜α＜0且β＜1，有：

（20）

当-1＜α＜0且β = 1，有：

（21）

其中：

（22）

定理3.2当  时，设z = x + iy，积分表达式

1）当  时：

2）当  时：

4  实验仿真

本节利用MATLAB对赖特函数的分区算法进行编程仿真，主要考察算法近似值与函数真实值的相对误差η = | （W - W真） / W真|×100%。取特例：

（23）

利用分区算法分别绘制 、 与真实值之间的相对误差，如图1、2所示。其中，分区算法在| z |≤0.95内采用泰勒级数计算，在0.95＜

| z |≤6内采用积分表达式计算，当| z |＞6时采用截断指数M = 10的渐近展开式计算。由图可观察：分区算法计算  时在| z |较小时使用积分表达式能取得高达1×10-13数量级的精度，但随着| z |不断增大后使用渐近展开式精度有所下降，但仍能保持1×10-11数量级的精度；对于 ，分区算法在整个矩形区域内至少取得1×10-12数量级的精度，对于大部分取值其精度能达到1×10-14数量级。

图1   与函数真实值的相对误差

图2   与函数真实值的相对误差

5  结  论

分数阶微积分由于具有时间记忆性和全局相關性被广泛应用于信号与信息处理、分数阶图像处理、控制系统等工程领域中来描述复杂现象。赖特函数作为一类新型特殊函数在分数微积分中有着重要地位，研究其性质与数值算法对于工程应用很有必要。本文将复平面划分三个区域，采用泰勒级数、积分表达和渐近展开数值技术来计算赖特函数，并基于MATLAB进行编程仿真。实验结果表明：分区算法的适用性广，能计算  范围内的参数；在计算精度方面，分区算法会受到参数α，β取值的影响而呈现不一样的精度，但均能达到较高精度；分区算法的积分表达式近似值在| z |较小时能有较高精度，但当赖特函数的值小于设置的精度时，积分表达式结果的误差会不断增加，渐近展开式不会受此限制，能够较精确地得到无限靠近0的赖特函数值。

分区算法研究仍存在许多值得探索的问题，比如：

1）算法中的区域划分参数q2及渐近展开式中的截断参数M的最佳取值还需要继续研究。

2）算法中积分表达式的准确性跟设置的误差容限与数值积分方式有很大联系，故还需研究最佳数值积分算法及误差容限参数设置。

3）由于数值积分及渐近展开需计算系数，该算法的运算速度较慢，如何提高算法运算效率还需进一步研究。

4）该算法仅实现赖特函数， 范围内的计算如何将范围扩展到  仍待研究。

参考文献：

[1] GORENFLO R，KILBAS A A，MAINARDI F，et al. Mittag-Leffler functions，related topics and applications [M].Berlin：Springer，2020.

[2] PODLUBNY I.分数微积分：理论基础与应用导论 [M].袁晓，译.北京：电子工业出版社，2021：106-113.

[3] 方宇孟.米塔-列夫勒函数的高精度快速算法和显示 [D].成都：四川大学，2022.

[4] WRIGHT E M. The asymptotic expansion of the generalized Bessel function [J].Proceedings of the London Mathematical Society，1935，38（1）：257-270.

[5] WRIGHT E M.The asymptotic expansion of the generalized hyper geometric function [J].Journal of the London Mathematical Society，1935，10（4）：287–293.

[6] WRIGHT E M. The generalized Bessel function of order greater than one [J].The Quarterly Journal of Mathematics，1940，11（1）：36-48.

[7] MAINARDI F，CONSIGLIO A. The Wright functions of the second kind in Mathematical Physics [J/OL].Mathematics，2020，8（6）：（2020-06-01）.https：//api.semanticscholar.org/CorpusID：219762246.

[8] POVSTENKO Y. Some applications of the wright function in continuum physics：A survey [J/OL].Mathematics，2021，9（2）：（2021-01-19）.https：//api.semanticscholar.org/CorpusID：234148001.

[9] CONSIGLIO A，LUCHKO Y，MAINARDI F. Some notes on the Wright functions in probability theory [J].WSEAS Transactions on Mathematics，2019，18：389-393.

[10] LUCHKO Y. Algorithms for evaluation of the Wright function for the real argumentsvalues [J].Fractional calculus and applied analysis，2008，11（1）：57-75.

[11] LUCHKO Y，Trujillo J，Velasco M P. The Wright function and its numerical evaluation [J].International Journal of Pure and Applied Mathematics，2010，64（4）：567-575.

[12] WONG R，ZHAO Y Q. Smoothing of Stokes' discontinuity for the generalized Bessel function [J].Proceedings of the Royal Society of London. Series A：Mathematical，Physical and Engineering Sciences，1999，455（1984）：1381-1400.

[13] WONG R，ZHAO Y Q. Smoothing of Stokes's discontinuity for the generalized Bessel function. II [J].Proceedings of the Royal Society of London. Series A：Mathematical，Physical and Engineering Sciences，1999，455（1988）：3065-3084.

[14] PARIS R B. Exponentially small expansions in the asymptotics of the Wright function [J].Journal of computational and applied mathematics，2010，234（2）：488-504.

[15] PARIS R B. Exponentially small expansions of the Wright function on the Stokes lines [J].Lithuanian Mathematical Journal，2014，54：82-105.

[16] PARIS R B. Asymptotic expansion of the Wright function for large variable and parameter [J/OL].arXiv：2110.06690 [math.CA].（2021-10-13）.https：//arxiv.org/abs/2110.06690.

[17] PARIS R B，Consiglio A，Mainardi F. On the asymptotics of Wright functions of the second kind [J].Fractional Calculus and Applied Analysis，2021，24（1）：54-72.

[18] NEMES G. Error bounds and exponential improvements for the asymptotic expansions of the gamma function and its reciprocal [J].Proceedings of the Royal Society of Edinburgh Section A：Mathematics，2015，145（3）：571-596.

[19] OLVER F W J. NIST handbook of mathematical functions hardback and CD-ROM [M].Cambridge：Cambridge university press，2010.

[20] ELEZOVI? N. Generalized Bernoulli polynomials and numbers，revisited [J].Mediterranean Journal of Mathematics，2016，13（1）：141-151.

[21] PARIS R B，KAMINSKI D. Asymptotics and mellin-barnes integrals [M].Cambridge：Cambridge University Press，2001.

[22] WRENCH J W. Concerning two series for the gamma function [J].Mathematics of Computation，1968，22（103）：617-626.

[23] PARIS R B. On the Asymptotic Expansion of Γ（x），Lagrange's Inversion Theorem and the Stirling Coefficients [J/OL].arXiv：1405.3423 [math.CA].（2014-05-14）.https：//arxiv.org/abs/1405.3423.

作者簡介：李燕（1995—），女，汉族，四川南充人，硕士研究生，研究方向：分数微积分理论与应用；袁晓（1964—），男，汉族，四川中江人，副教授，博士，研究方向：现代信息信号处理、分数微积分理论与应用、现代电路与系统理论与技术。