基于双目视觉的球形物体运动轨迹重建

施博凯 张昕 张志鹏 宁洪龙 邱天

收稿日期：2023-08-02

基金项目：2019年广东省拨款高校建设“冲补强”专项基金；五邑大学高级人才科研启动基金2019（5041700171）；2021年江门市创新实践博士后课题研究资助项目（JMBSH2021B04）；广东省重点领域研发计划（2020B0101030002）；2020五邑大学大学生创新创业计划（202011349186）

DOI：10.19850/j.cnki.2096-4706.2024.05.021

摘  要：文章介绍了一种改进的球形目标运动轨迹拟合算法，并以高尔夫球为实例进行算法验证。针对三次样条插值曲线平滑性较弱问题，提出一种基于滤波降噪的改进插值算法，实验结果表明该算法对插值结果影响细微的情况下平滑了拟合曲线。实验首先检测出球心坐标，在双目序列图像之间根据坐标差异进行空间点的三维重建；再用一种基于Savitzky-Golay滤波的三次样条插值算法将高尔夫球在空间中的三维散点进行非线性拟合处理，最终完成运动轨迹的三维重建。通过模拟实验，与传统算法相比，文章提出的改进算法恢复运动物体三维信息的效果更加显著，且平均误差率在5%以内。

关键词：三维重建；目标检测；Savitzky-Golay滤波；三次样条插值

中图分类号：TP391    文献标识码：A  文章编号：2096-4706（2024）05-0094-08

Reconstruction of Spherical Object Motion Trajectory Based on Binocular Vision

SHI Bokai1， ZHANG Xin1， ZHANG Zhipeng1， NING Honglong2， QIU Tian1

（1.Joint Laboratory of Digital Optical Chips， Institute of Semiconductors， Chinese Academy of Sciences， Wuyi University， Jiangmen  529020， China; 2.State Key Laboratory of Luminescent Materials and Devices， Institute of Polymer Optoelectronic Materials and Devices， School of Materials Science and Engineering， South China University of Technology， Guangzhou  510640， China）

Abstract： This paper introduces an improved algorithm for fitting the movement trajectory of spherical targets， and validates the algorithm with a golf ball as an example. Aiming at the problem of weak smoothness of cubic Spline interpolation curve， an improved interpolation algorithm based on filtering noise reduction is proposed. The experimental results show that the algorithm smoothes the fitting curve when the effect of the algorithm on the interpolation result is slight. Firstly， the spherical center coordinates are detected， and the 3D reconstruction of spatial points is performed between binocular sequence images according to the coordinate difference; Then a cubic Spline interpolation algorithm based on Savitzky Golay filtering is used to nonlinear fit the golf ball's 3D scattered points in space， and finally the 3D reconstruction of the motion trajectory is completed. Through simulation experiments， compared with the traditional algorithm， the improved algorithm proposed in this paper has a more significant effect in restoring the 3D information of moving objects， and the average error rate is less than 5%.

Keywords： 3D reconstruction; object detection; Savitzky-Golay filtering; Cubic Spline Interpolation

0  引  言

三維重建是一种计算机图形学和计算机视觉领域的技术，用于从多个二维图像或其他数据源中恢复物体或场景的三维模型。三维重建刚开始主要针对静态物体，随着时间推移，技术逐渐发展，在重建动态物体的运动轨迹方面也有很好的效果。高尔夫运动在世界范围内已经逐渐发展到大众化的运动，吸引了大量的观众和参与者[1]，所以本文以高尔夫球作为具体化的球形目标进行实验和研究。

三维重建技术主要分为基于几何结构的重建方法和基于图像的重建方法两种。基于几何结构的三维重建方法是根据物体的几何形状、尺寸和位置等信息进行重建的，常见的算法有点云法、体素法、多视图立体匹配法等；基于图像的重建方法则通过对多张图像进行解析计算，还原出物体的三维信息。目前利用图像进行三维重建主要研究方向为单目视觉与双目视觉。其中双目视觉也称立体视觉（stereopsis），是基于生物学原理模拟人类双眼，利用两个摄像头在同一场景下拍摄得到图像，根据视觉差异，通过对比计算两个图像的像素信息，之后推断出物体的深度信息，继而重建出三维场景。本文基于双目立体视觉系统进行研究。

本文利用左、右摄像头拍摄的高尔夫球双目序列图像，首先进行相机标定，获取两相机的参数，之后定位出球心在图像中的坐标，最后通过立体视觉恢复高尔夫球在运动中的三维信息。使用双目视觉三维重建的方法可以恢复高尔夫球的运动轨迹，对初学者矫正击球方式、运动员做赛前训练与赛后复盘能发挥很大的作用。

1  目标检测

1.1  方法简介

近年来，随着计算机视觉技术的发展，作为其中重要组成部分之一的运动目标检测技術，在视觉领域得到了研究学者的广泛关注，并在体育赛事、国防监测等方向得到应用[2-4]。运动目标检测是将图像序列或一段视频中发生位置变化的物体作为前景标记出来的过程，它可以对需要检测的对象进行识别、跟踪、定位等行为。在体育项目中，背景差分法是常用且有效的目标检测方法之一，通过从图像序列当前帧减去背景模型来检测前景目标，可以快速检测出感兴趣目标[5]。

在传统算法领域主流的目标检测算法有背景差分法、帧间差分法和光流法。由于光流法的计算量大，处理时间长，无法实现实时检测，对场景光线变化较为敏感；帧间差分法虽然实现简单，检测速度快，但缺点在于需要准确地选择帧间间隔，帧间间隔在很大程度上会影响目标检测的精确程度。背景差分法因其计算量少，实时性强而被研究学者与从事视觉相关工作人员广泛应用。

背景差分法是目标检测的一个重要技术，用于从静态摄像机中检测移动物体与视频监控处理等领域。该方法的基本原理是根据当前帧和参考帧之间的差异检测运动物体，此参考帧通常称为“背景图像”或“背景模型”[6，7]。帧间差分法是将图像序列或视频序列相邻帧进行差分以检测目标的一种图像处理技术。当相邻帧产生明显变化时，即意味着目标的位置发生改变，此时目标开始运动，通过差分连续帧得到差分图像，之后与自定义阈值作对比，将图像二值化，以此定位出运动目标。本文通过对比背景差分法与帧间差分法的效果，选择更优的目标检测算法用于检测球心。精确的球心检测是空间点三维重建的前提，保障了后续运动轨迹拟合的效果。

1.2  背景差分法

1.2.1  背景建模

背景差分法的关键技术在于背景模型的建立，其中一种常用的算法是基于高斯模型实时更新背景。虽然混合高斯模型（Gaussian Mixture Model， GMM）具有灵活的参数调节能力——可以通过调整高斯分布的数量、权重和参数等来适应不同场景的背景特点，从而提高算法的性能和鲁棒性。但是缺点也相应地比较明显——计算复杂度高，降低目标检测的实时性。而单高斯模型（Single Gaussian Model， SGM）实现简单，适用于室内场景，因此本文使用单高斯模型进行背景建模，符合后续三维重建实时性的要求。

对一个背景图像，特定像素亮度的分布满足高斯分布，即对背景图像A，每一个点（x，y）的亮度满足A（x，y）～N（μ，d）：

（1）

式（1）中μ为数据的均值，d为数据的标准差。计算一段时间内的视频序列图像中每一个像素点的均值μ和方差d，作为背景模型。假设一幅图像G，其包含前景，对于图像上的每一个点（x，y）计算，若：

（2）

在式（2）中，T为一个设定好的阈值，当不等式成立时，将该点标记为背景点，反之则为前景点。将每一帧图像都进行背景的更新：

（3）

其中，p为常数，表示背景更新率，p的大小与更新速度成反比。通常情况下，背景更新后p不再更新。

在实时处理过程中，对于每个像素，将当前帧图像的像素值与背景模型进行比较。如果像素值与背景模型之间的差异小于一个设定的阈值，将该像素标记为背景；否则，将其标记为前景。

通过更新背景模型的均值和标准差，可以适应背景的变化。当一个像素被确定为背景时，可以通过以下算式更新背景模型：

（4）

（5）

在上式中，、 为更新后的均值和标准差，μt-1、dt-1为旧的均值和标准差，x为当前像素值，ρ为参数的更新速率，也称参数学习率。

通过不断更新背景模型，可以适应背景的变化，并降低背景变化引起的误检率。

1.2.2  背景差分

本文所处实验环境为室内，场景的环境光基本上全程保持一致，在高尔夫球的运动过程中，运动中的球与背景之间存在差异，利用背景差分法即可得到差分灰度图像。差分灰度图像包含了运动目标信息，相对于背景图像又称为前景图像[8]。

假设前景图像为g （x，y），当前帧输入图像为f1 （x，y），背景图像为f2 （x，y）。则可以表示为：

（6）

在进行背景差分法处理时，像素点的差值可能会存在负值的情况，为了避免这种情况的出现，可以进行截断处理：即当g （x，y）＜0时，像素点仍取0。但此方法会令新图像整体偏暗，不利于后续阈值分割的处理。

在本文提出的背景差分法中，选择取绝对值的方法对负值进行处理，如式（7）所示：

（7）

由上式可知：前景图像可以概括为当前帧的运动目标与背景图像差值的绝对值。背景差分法可以用来显示两幅图像之间的差异，不仅可以应用在前景运动目标的检测上，也可以检测视频镜头边界。

1.3  帧间差分法

在本文中，对图像序列进行帧间差分。差分算式如下：

（8）

（9）

在上式中，Dm （x，y）为差分结果图像，Fm （x，y）为第k帧图像，Fm-1 （x，y）为第k-1帧图像，Bm （x，y）为二值图像，T为阈值。当差分图像中某像素点的值小于T，则认为该点是静止的，该点被判为背景点；若大于等于阈值T，则认为该点非静止，该点标记为目标点。

上述为使用相邻两个连续帧进行差分的情况，即二帧差分法。虽然原理简单，计算量小，但存在以下缺点：鲁棒性较差，二帧差分法对噪声比较敏感，当背景复杂或者存在噪声时，可能会产生误检测或者漏检测的问题；对于高速运动的物体，二帧差分会使分割区域远大于待检测目标；相邻的两个连续帧差分可能导致两帧中待检测目标重叠部分一并差分，造成空洞。

鉴于二帧差分法存在的缺点，使用三帧差分法可以改善图像的处理效果。三帧差分法在二幀差分法的基础上，将相邻的每三帧图像作为一组进行差分。相比于二帧差分法，三帧差分法对快速运动物体的检测能力更强，可以更精确地捕捉到快速运动物体的变化，提高目标检测的精度[9]。

设相邻的连续三帧图像为Fm-1、Fm、Fm+1，根据二帧差分法的公式算出相邻两帧的差分图像，算式如下：

（10）

（11）

（12）

（13）

在上式中，Dm+1 （x，y）、Dm （x，y）为相应帧的差分结果图像，Bm+1 （x，y）、Bm （x，y）为相应帧的二值图像，T为阈值，根据上式可得运动目标的二值图像，如式（14）所示：

（14）

移动物体的检测是一项识别物体在特定区域中运动的技术，是计算机视觉和视频处理领域非常重要和有效的研究课题，因为它是许多复杂过程的关键步骤，如序列图像对象检测和视频跟踪活动。因此，本文研究双目序列图像中移动目标的检测并进行精准定位具有重要意义[10]。

2  三维重建

本文涉及的三维重建技术为基于双目视觉的三维重建，通常情况下基于双目视觉的三维重建需要经过图像获取、相机双目标定、双目校正、双目匹配等步骤，最终完成三维重建。

相机双目标定的作用是获取相机的内参数，如焦距（focal length）、主点（principal point）、畸变系数（distortion coefficient）和外参数，如两相机之间的旋转矩阵与平移向量，用于表示二维像素点与空间点的映射关系[11]。

理想情况下，双目视觉的两个相机共面且光轴平行，参数相同，但是在实际操作中难以实现，因为两个相机在安装时无法看到光轴和成像平面。

三维空间点成像的模型如图1所示，空间中任意一点P，分别用C1和C2两个摄像头同时拍摄P点，P在两平面上的投影点分别为P1、P2，且已解决图像配准问题——P1、P2为相互匹配的两个点，由此可得：P点为直线C1P1与直线C2P2的交点，它的三维位置是唯一确定的。

图1  三维空间点成像模型

双目校正是根据相机双目标定后获得的内、外参数和两个相机相对位置，对左右视图消除畸变影响以及行对准的操作。校正的目的是把两个不同方向的图像平面重新投影到同一个平面且光轴互相平行，转化为理想情况的模型。双目校正操作后的成像模型如图2所示，经过校正的双目相机成像共面且光轴互相平行。

图2  校正后三维空间成像模型

双目匹配是指通过比较两个摄像头拍摄的图像，找到相互匹配的像素点，计算得到图像中物体的深度信息。也称立体匹配。双目匹配的目标是找到左、右图像中对应的像素点之间的视差值，即左、右像素的水平位移差异，通过视差值推测出物体在图像中的深度[12]。

在本文中，将高尔夫球运动轨迹的三维重建转化为一系列空间点的三维重建。其中，相机的双目标定是必须进行的操作，用于确定两个相机的内、外参数，以便进行后续三维坐标的计算。双目校正与双目匹配可以省略，这两个操作的主要目的是减少计算量，已知两个相机中的高尔夫球球心在三维空间中代表同一点，这种情况下只需要根据相机标定建立的世界坐标系到像素坐标系对应的投影矩阵，利用最小二乘法求取物体三维空间点的坐标即可完成高尔夫球的三维重建。本文已解决图像配准问题，即左右相机拍摄到的图像中的高尔夫球心代表空间中的同一点，空间点三维重建的基本模型如图3所示。

图3  空间点三维重建模型

空间中任意一点P在左、右相机上的投影坐标记为P1P2，它们的在相机平面上的投影坐标分别记为

P1（u1，v1）、P2（u2，v2），投影矩阵分别为M1、M2：

（15）

（16）

则对左、右相机有：

（17）

（18）

在上式中，Zc1、Zc2分别为左、右相机坐标系上的Z坐标，（u1，v1）、（u2，v2）分别为左、右相机所拍摄图像上的像素坐标，（X，Y，Z，1）为P点在世界坐标系下的齐次坐标， 分别为Mk的第i行第j列元素。联立式（17）与式（18）可以消去Zc1、Zc2，得到：

（19）

使用最小二乘法即可解出X，Y，Z三个未知数，即为P点的三维坐标（X，Y，Z）。

3  基于Savitzky-Golay滤波的三次样条插值法

3.1  三次样条插值

三次样条插值是一种常用的数值插值方法，用于在给定一组离散数据点的情况下，通过一组三次多项式来逼近这些数据点，从而得到一个平滑的曲线。三次样条插值的优点是可以在保持平滑性的同时，避免了其他插值方法可能引起的振荡和不稳定性。三次样条插值的基本思想是将插值区间内的每个小区间拟合成一个三次多项式，使得整体曲线在这些小区间内既能够经过给定的数据点，又保持平滑。

假设[a，b]区间内有：a = x0＜x1＜x2＜…＜xn = b，存在函数S （x），使得：

1）在每个子区间[xi， xi+1]（i = 0， 1， 2， …， n-1）上S （x）是三次多项式。

2）在[a，b]区间上有1阶、2阶导数。则称S （x）为区间[a，b]上的三次样条函数，可以构造方程：

（20）

其中ai，bi，ci，di为未知数，有n个小区间，则有4n个未知数，称这个方程为三次样条函数，且S （x）满足以下条件：

1）所有点均满足插值条件：S （x） = yi（i = 0，1，…，n），除了左右两个端点，剩下n-1个点皆满足Si （xi+1） = yi+1，Si+1 （xi+1） = yi+1这两个方程，由此可得2n-2个方程，此外左右两个端点满足第一与最后一个方程，则总共有2n个方程。

2）由于n-1个内部点的一阶导数连续，即在第i区间的终点和第i+1区间的起点为同一点，其一阶导数相等，即 ，由此条件可得n-1个方程。

3）n-1个内部点的二阶导数连续，即 ，由此可得n-1个方程，综上有4n-2个方程。

根据以上4n-2个条件，再加上边界条件：，即自然边界，即可求解4n个方程，求出y的表达式。

尽管三次样条插值稳定性好，且分段插值可以有效避免Runge现象，在工程中具有广泛应用[13]。但是三次样条插值只能保证各小区间的连续性，无法保证整条插值曲线的光滑性，且在某些情况下可能出现振荡现象。特别是当数据点之间存在噪音时，插值曲线会过度适应数据，导致插值函数在数据点之间振荡。

3.2  Savitzky-Golay滤波

噪声是信号或数据中的无用信息，它是在测量、传输、采集或处理过程中受到的随机扰动。在现实世界中，我们经常会遇到各种形式的噪声，它们可能来自环境、传感器、设备、通信通道等。所以，降噪处理一直是图像处理和计算机视觉研究的热点[14]。对曲线进行平滑降噪是一种基本图像处理方法，将曲线上每个点的数值替换为该点及其邻域一定范围内点的平均值，从而去除高频噪声，使曲线更加平滑[15]。

Savitzky-Golay滤波是一种数字信号处理中常用的平滑滤波方法，它采用多项式拟合的方式对信号进行平滑处理。这种滤波方法适用于平滑时间序列信号或曲线，并且能够保留信号的整体特征，同时去除高频噪声成分，即在消去噪声的同时保持信号的宽度与形状[16]。

定义一个宽度为n = 2m + 1的窗口，对曲线由左向右进行测量。窗口自左至右滑动，直至拟合完所有数据点。拟合后的曲线即被去除了原有的高频分量。假设一组2m + 1个数据，其以数据点yt为中心，对这组数据点进行k-1次多项式的拟合，如式（21）所示：

（21）

求解上述方程，需要令n＞k。由2m + 1个数据，分别有2m + 1个方程，可以将拟合方程改写为矩阵形式，如式（22）所示：

（22）

其中Y為数据值向量，A为系数矩阵，X为自变量矩阵，ε为残差。式（22）可以通过最小二乘法解得稀疏矩阵为 ，其值如式（23）所示，拟合后的数据预测值为 ，其值如式（24）所示：

（23）

（24）

3.3  算法流程

在运动中由于击球速度较快，但受限于本实验使用的双目相机拍摄帧数不高，球的一次运动中拍摄得到的图片数量较少，对空间点进行三维重建得到的坐标数量不足以对整个运动过程进行重建，需要用插值法对数据进行模拟补全。

插值法在图像处理和信号处理、科学计算等领域中是非常常用的一项技术，是从已知点近似计算未知点的近似计算方法，即构造一个多项式函数，使其通过所有已知点，然后用求得的函数预测位置点。本文使用基于Savitzky-Golay滤波的三次样条插值解决运动轨迹拟合问题，算法流程如图4所示。

图4  算法流程

4  实验结果

4.1  相机标定结果

使用MATLAB工具箱里“Stereo Camera Calibrator”进行标定，两个相机在三维空间中的相对位置如图5所示，可以看到两个相机在场景中分开放置，光心不在同一水平线上，极线不平行且不共面。

通过标定得到两个相机的内参矩阵I1、I2，畸变系数D1、D2，以及两相机之间的旋转矩阵r与平移向量t，算式如下：

（25）

（26）

（27）

（28）

（29）

（30）

图5  两个相机的相对位置

4.2  球心检测结果

图6为三种运动目标检测算法的结果，分别是二帧差分法、三帧差分法、背景差分法。

图6（a）为球体在某次运动中其中一帧图像；图6（b）为二帧差分法检测球体的结果，可以看到图中存在两个物体，这种现象也称为“鬼影”，即在物体原来的位置和现在的位置都出现该物体，这是因为球速过快，相邻两帧的差分不足以检测出目标，在运动目标速度较快的情况下，二帧差分法不适用；图6（c）为三帧差分法的检测结果，虽然将差分的帧间间隔定为三帧后解决了“鬼影”现象，但是检测出来的物体不完整；图6（d）为背景差分法的检测结果，通过该帧图像与背景进行差分，之后通过简单的图像处理即可定位出球体，目标检测的精确程度与后续空间点三维重建的效果是密切相关的。

（a）第11幀原图        （b）二帧差分法检测结果

（c）三帧差分法检测结果     （d）背景差分法检测结果

图6  不同算法检测结果对比

4.3  运动轨迹拟合结果

将球体在一次运动中检测出来的球心序列图像按照本文算法重建出其三维坐标，如表1所示。

表1  序列图像球心二维坐标及三维坐标

帧数 左摄像头

（u1，v1） 右摄像头

（u2，v2） 三维坐标（x，y，z）

1 （397，202） （440，239） （478.19，80.10，3 016.59）

2 （343，201） （374，231） （330.18，67.23，3 080.98）

3 （232，199） （263，219） （32.93，58.55，3 128.95）

4 （127，197） （152，206） （-259.36，48.87，3 175.99）

5 （26，195） （43，194） （-547.50，40.43，3 222.69）

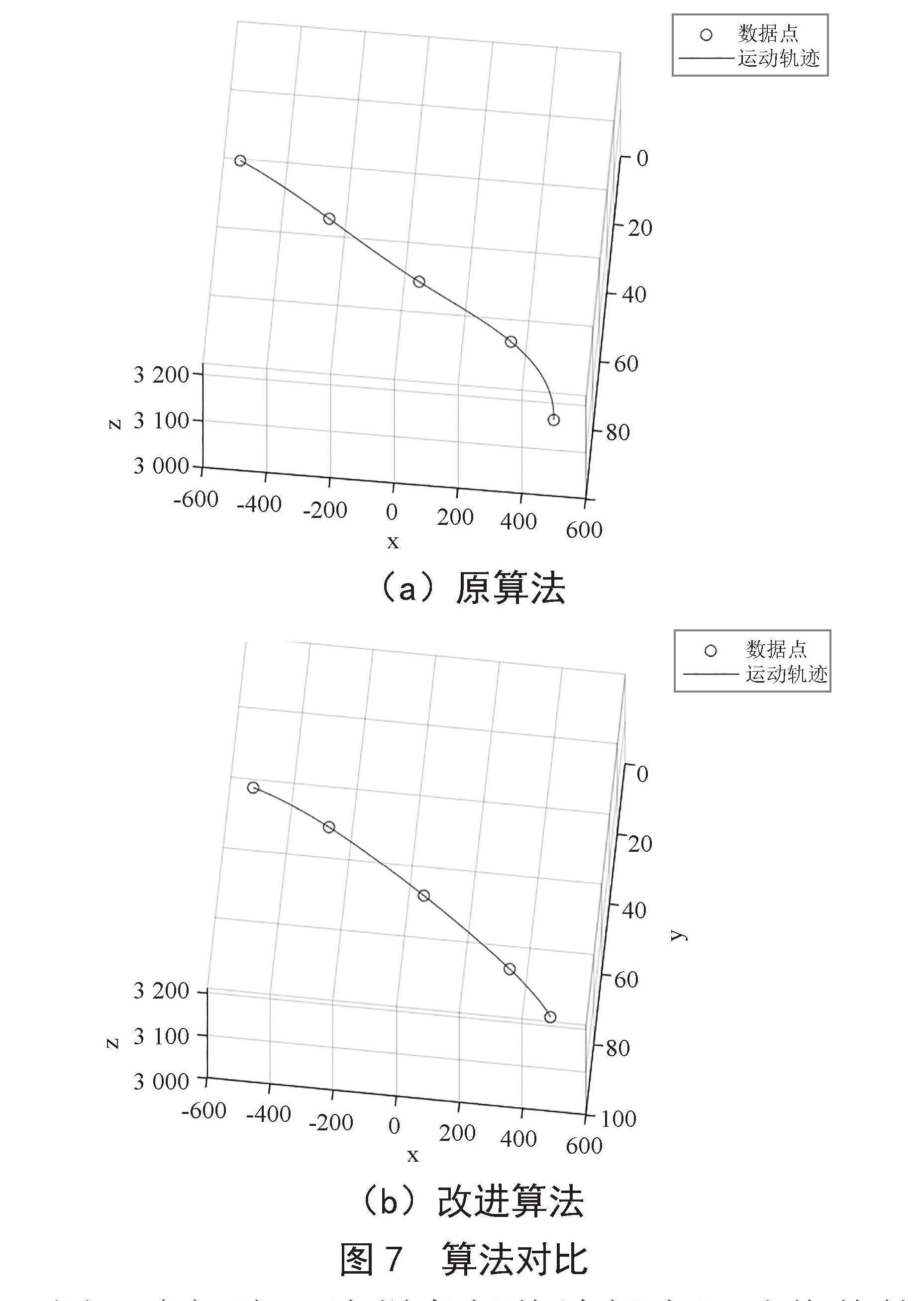
将三维坐标用MATLAB软件拟合出轨迹，其运动轨迹如图7所示。

（a）原算法

（b）改进算法

图7  算法对比

图7（a）为三次样条插值法拟合运动物体轨迹的结果，其轨迹为一条形状不规则的曲线，由于球体运动的物理模型是非线性的，观测会受到噪声的干扰，影响球体运动轨迹的拟合结果；图7（b）为本文提出改进算法拟合轨迹的结果，对三维散点进行基于SG滤波的三次样条插值法，之后拟合所有点，结果为一条规则的抛物线。

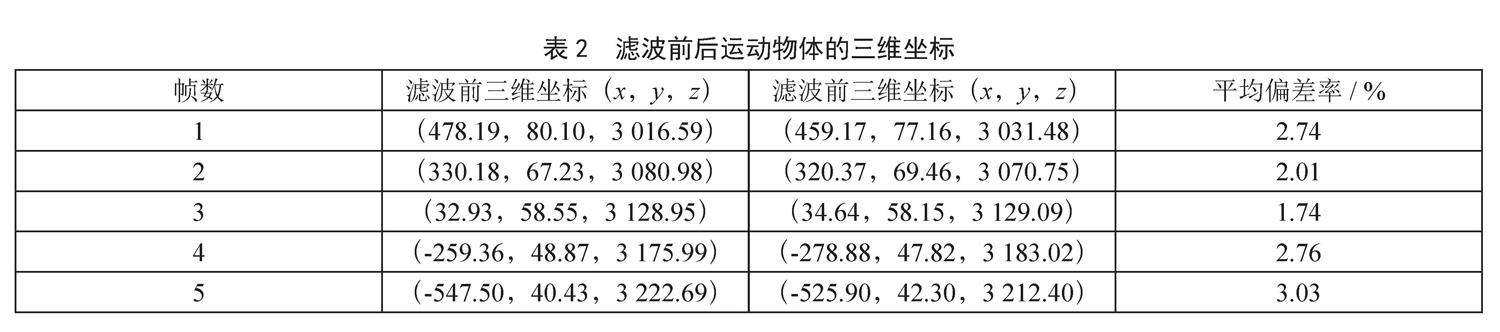
滤波前后该物体的三维坐标如表2所示。

滤波后的三维坐标中x、y、z三个分量与滤波前的平均偏差率不超过3.5%，在很好地恢复了物体运动轨迹的基础上不会丢失过多的精度，在对精度要求不高的系统内可以出色地完成需求。

4.4  模拟实验结果

受到实验条件的限制，测量物体在三维空间中的真实坐标存在一定困难，由此本文设计了一个模拟实验用于判定系统误差，内容如下：

1）采集离双目摄像头有一定距离的棋盘格序列图像。

2）重新进行相机标定。

3）假设物体在棋盘格上做如图8所示的运动，拟合出其轨迹。

4）将计算值与真实值做对比，计算出误差率。

将棋盘格放在离摄像头40 cm处，模拟棋子在棋盘格上从点A运动到点E，路径如图9所示，路径与棋盘格的交点分别为A、B、C、D、E，且每个格子的边长为22 mm，用本文改进算法重建出三维坐标，数据如表3所示。

在表3中，距离与三维坐标的单位均为毫米（mm），其中z轴代表物体与摄像头之间的距离，误差率的计算方式为：误差率= |真实距离-测量距离| /真实距离。由表3可以看出该系统的平均误差率不超过5%，本文提出的改进算法对精度只产生细微影响。

将以上数据拟合成运动轨迹，使用MATLAB拟合运动轨迹的结果如图9所示，其形状为一条拱形抛物线，符合模拟实验的预期效果。

图8  物体在棋盘格上的运动轨迹

图9  改进算法拟合轨迹

5  结  论

本文利用双目图像序列对球形目标在空间中的运动轨迹进行三维重建，对比了背景差分法、二帧差分法、三帧差分法的算法效果，选择使用背景差分法做目标检测；针对三次样条插值法生成数据与观测非线性运动过程存在噪声，提出一种基于Savitzky-Golay滤波的改进三次样条插值法进行降噪并平滑插值曲线，通过数据可视化体现出改进算法的优势。

通过本文实现的三维重建可以得到球形目标在空间中的三维信息，对球体运动轨迹的跟踪与分析，拟合出球的运动轨迹可以帮助运动员对击球的角度、力度、姿势等进行调整，也可以帮助初学者矫正错误击球方式，取得进步。模拟实验结果表明，本文提出的算法对恢复物体运动轨迹的形状效果显著。在目标检测方面，可以通过基于深度学习的方法进一步提升处理速度与精度，后续将围绕其展开研究。

参考文献：

[1] ZHANG X H，ZHANG T X，YANG Y J，et al. Real-time Golf Ball Detection and Tracking Based on Convolutional Neural Networks [C]//2020 IEEE International Conference on Systems，Man，and Cybernetics （SMC）.Toronto：IEEE，2020：2808-2813.

[2] FAN H Y，HU Y H，ZHANG J F. Automatic Capture Processing Method of Basketball Shooting Trajectory Based on Background Elimination Technology [J].Advances in Meteorology，2022，2022：7884528.

[3] HIGAKI S，HORIHATA K，SUZUKI C，et al. Estrus Detection Using Background Image Subtraction Technique in Tie-Stalled Cows [J].Animals，2021，11（6）：1795.

[4] WANG J M，CHEN J H. An Improved Background Subtraction Method for Adaptive Rate Compressive Sensing [J].Journal of Physics： Conference Series，2021，1914（1）：012024.

[5] HOU J B，LI B G. Swimming Target Detection and Tracking Technology in Video Image Processing [J].Microprocessors and Microsystems，2021，80：103535.

[6] MCIVOR A M. Background Subtraction Techniques [J].Image and Vision Computing，2000，4：3099-3104.

[7] PICCARDI M. Background Subtraction Techniques：A Review [C]//2004 IEEE International Conference on Systems，Man and Cybernetics （IEEE Cat No 04CH37583）.The Hague：IEEE，2004，4：3099-3104.

[8] 彭接力，刘岩.物体融入背景情况下的目标检测方法 [J].电子科技，2012，25（11）：102-104+108.

[9] 韩帅.基于改进帧间差分法与背景差分法车辆检测 [J].农业装备与车辆工程，2021，59（6）：88-92.

[10] KULCHANDANI J S，DANGARWALA K J. Moving Object Detection： Review of Recent Research Trends [C]//2015 International Conference on Pervasive Computing （ICPC）.Pune：IEEE，2015：1-5.

[11] VO M N，WANG Z Y，LUU L，et al. Advanced Geometric Camera Calibration for Machine Vision [J].Optical Engineering，2011，50（11）：110503.1-110503.3.

[12] 王迪迪，候嘉豪，王富全，等.基于双目视觉的目标检测与测距研究 [J].电子制作，2022，30（21）：58-61.

[13] 高晓，杨志强，库新勃，等.基于三次样条插值实现无人机高动态运动轨迹插值 [J].全球定位系统，2020，45（1）：37-42.

[14] 唐娅琴.几种图像平滑去噪方法的比较 [J].西南大学学报：自然科学版，2009，31（11）：125-128.

[15] 雷林平.基于Savitzky-Golay算法的曲线平滑去噪 [J].电脑与信息技术，2014，22（5）：30-31.

[16] GORRY P A. General Least-squares Smoothing and Differentiation of Nonuniformly Spaced Data by the Convolution Method [J].Analytical Chemistry，1991，63（5）：534-536.

作者簡介：施博凯（1998—），男，汉族，广东汕尾人，硕士在读，研究方向：图像处理；通讯作者：邱天（1977—），男，汉族，河南周口人，副教授，博士，研究方向：图像处理、集成电路设计及智能设备等。