基于PSO-LSTM的区域二手房价预测方法研究

周昌堉 李长云

收稿日期：2023-12-19

DOI：10.19850/j.cnki.2096-4706.2024.05.022

摘  要：探究房价趋势是一个高度复杂且充满非线性特征的研究难题。针对目前二手房价预测精度低的问题，文章提出了基于PSO-LSTM的区域二手房价预测方法。粒子群算法通过对LSTM模型进行优化，找到最优的参数组带入PSO-LSTM模型中，进而得到更符合实际情况的预测结果。文章通过湖南省株洲市天元区的二手房价时间序列数据集对PSO-LSTM模型进行训练，并与LSTM神经网络模型进行了对照分析。实验结果显示，PSO-LSTM模型对于区域二手房价的预测精度更优。

关键词：区域二手房价预测；时间序列；PSO-LSTM模型；LSTM

中图分类号：TP18    文献标识码：A    文章编号：2096-4706（2024）05-0102-05

Research on Regional Second-hand Housing Price Prediction Method Based on PSO-LSTM

ZHOU Changyu， LI Changyun

（Hunan University of Technology， Zhuzhou  412007， China）

Abstract： Exploring the trend of housing prices is a highly complex and full of nonlinear features research challenge. Aiming at the current problem of low accuracy of second-hand housing price prediction， this paper proposes a regional second-hand housing price prediction method based on PSO-LSTM. The Particle Swarm Optimization optimizes the LSTM model to find the optimal parameter group and incorporate it into the PSO-LSTM model， and then get the prediction results that are more in line with the actual situation. In this paper， the PSO-LSTM model is trained by the time series dataset of second-hand housing price in Tianyuan District， Zhuzhou City， Hunan Province， and the PSO-LSTM model is analyzed against the LSTM neural network model. The experimental results show that the PSO-LSTM model has better prediction accuracy for regional second-hand housing prices.

Keywords： regional second-hand housing price prediction; time series; PSO-LSTM model; LSTM

0  引  言

在当今数字化时代，房地产市场一直以来都是全球经济的一个关键组成部分。二手房价的波动不仅影响着个人和家庭的财务状况，还对全球金融市场和城市规划产生深刻的影响。对于政府、投资者、开发商和一般居民而言，准确预测二手房价变得愈加重要。二手房价的准确预测有助于投资者做出明智的决策，卖家可以更好地定价房产，政府能够更好地规划城市发展，金融机构则可以更有效地管理风险。然而，房价波动受到众多复杂因素的影响，这使得预测二手房价变得复杂而具有挑战性。

对于预测模型，早期的学者多采用的自回归模型来进行预测，如AR、ARMA、ARIMA[1]等，但因二手房价影响因素复杂，波动也比较大，故预测的模型不能很好地将二手房价的趋势反映出来。而随着互联网时代的發展，科学的预测方法也越来越多样化。目前，常用的预测方法多是时间序列预测方法。其通过时间将数据进行排序，再通过数据之间的变化关系进行自主学习。其中长短时记忆模型[2]（Long Short-Term Memory， LSTM）在时间序列数据分析中崭露头角，已经广泛应用于众多领域。蔡兆晖[3]等引入LSTM神经网络，对大宗商品时序数列进行自适应最优项数分解，显著改善了大宗商品价格预测的准确性。许钰林[4]等采用深度LSTM模型，对玉米和大豆期货价格进行预测，提升了单个农产品期货模型的预测性能，为农产品领域提供了高精度的预测模型。程先龙[5]等使用LSTM组合模型对我国西南某风电场的实测数据进行预测，有效提高了风电功率预测精度。方雪清[6]等使用LSTM的短期组合预测模型，对广州市江南农副产品市场的富士苹果日价格进行分析预测，证明了LSTM的短期组合预测模型对农产品价格的短期预测具有一定的优势。高华睿[7]等通过LSTM的组合模型，对高速公路的交通流进行短时预测，模型的精度和泛化能力高，为高速公路短时交通流预测提供一种新的参考思路。上述表明LSTM[8]神经网络在时间序列数据预测的优越能力，能够有效捕捉时间序列中的依赖关系，并且能够很好地处理传统网络模型的梯度爆炸等问题。但是参数的选择对LSTM神经网络模型具有很大的影响，参数取值不当会导致模型欠拟合或者过度拟合，进而导致预测精度的不准确。

本文针对上述问题，提出了基于PSO-LSTM的区域二手房价预测方法。通过获取湖南省株洲市某区2015年4月至2022年12月售房网站的二手房价数据，对该数据进行预处理，构建LSTM神经网络模型，通过粒子群算法[9]对LSTM模型的参数进行全局搜索最优和优化，以实现预测精度的提高。运用该模型进行区域二手房价的预测，并与LSTM模型进行预测评估指标的比对分析，进而获得预测区域二手房价的优化模型。

1  研究方法

1.1  LSTM原理

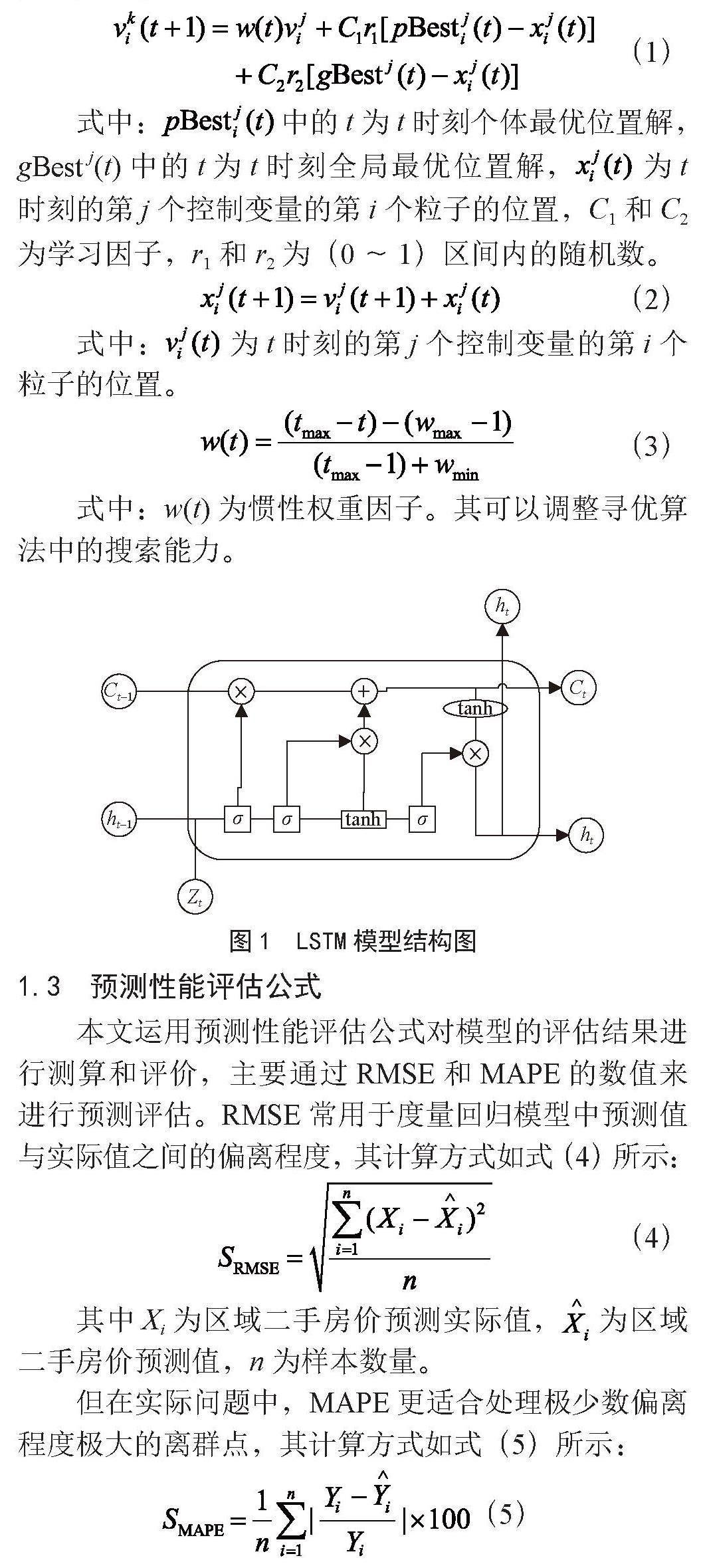
LSTM是对RNN的改进，成功应对了梯度消失和梯度爆炸问题，尤其在时间序列数据处理中具有显著优势，图1为LSTM模型结构图。LSTM单元的组成[10]包括遗忘门、输入门、输出门和细胞状态。遗忘门、输入门和输出门是神经网络中的关键元素，它们各自担负着不同的责任，以确保网络能够高效地处理信息。遗忘门负责过滤当前单元的记忆，决定丢弃哪些信息以适应新的输入。输入门则负责控制新信息的引入，以更新当前单元的状态。最后，输出门则掌握着当前单元输出哪些特征信息的控制权，以使网络的输出与任务需求相匹配。这三个门协同工作，使神经网络能够在不同时间步骤中有效地管理信息流，从而提高模型的性能和适用性。它们是深度学习中的关键组件，有助于实现更好的序列建模、自然语言处理、语音识别等任务。这种门控机制的使用使得神经网络能够更好地处理时序数据和长期依赖关系，为各种应用领域带来了显著的改进。通过组合三门等门控单元以实现信息的安全和当前状态的更新。LSTM能够将原始时间步长的有效信息传递到后续时间步长，从而克服了短时记忆的问题，改进了传统RNN的限制。因此将复杂的时序序列数据通过LSTM进行大量训练，其能够更好地分辨数据的保留或删除。LSTM神经网络的性能受超参数的影响，通过调整超参数，以实现模型的稳定收敛并获得可靠的实验结果。

1.2  粒子群算法

粒子群优化算法（Particle Swarm Optimization， PSO），是由Kennedy和Russell Eberhart于1995年提出的一种改进的全局寻优的算法[11]，起源于对大自然中的鸟群或鱼群等生物群体觅食行为的研究。把每只鸟看作是一个粒子，其在空间范围内不停运动，每个粒子拥有适应自身的速度和位置，空间中的粒子通过追搜寻最佳位置，不断跟踪和保存空间内最优粒子位置，从而得到全局最优解的过程实现。PSO算法式子如下：

（1）

式中： 中的t为t时刻个体最优位置解，gBest j（t）中的t为t时刻全局最优位置解， 为t时刻的第j个控制变量的第i个粒子的位置，C1和C2为学习因子，r1和r2为（0～1）区间内的随机数。

（2）

式中： 为t时刻的第j个控制变量的第i个粒子的位置。

（3）

式中：w（t）为惯性权重因子。其可以调整寻优算法中的搜索能力。

图1  LSTM模型结构图

1.3  预测性能评估公式

本文运用预测性能评估公式对模型的评估结果进行测算和评价，主要通过RMSE和MAPE的数值来进行预测评估。RMSE常用于度量回归模型中预测值与实际值之间的偏离程度，其计算方式如式（4）所示：

（4）

其中Xi为区域二手房价预测实际值， 为区域二手房价预测值，n为样本数量。

但在实际问题中，MAPE更适合处理极少数偏离程度极大的离群点，其计算方式如式（5）所示：

（5）

其中Yi为区域二手房价预测实际值， 为区域二手房价预测值，n为样本数量。

2  PSO-LSTM优化方法

2.1  数据集选择

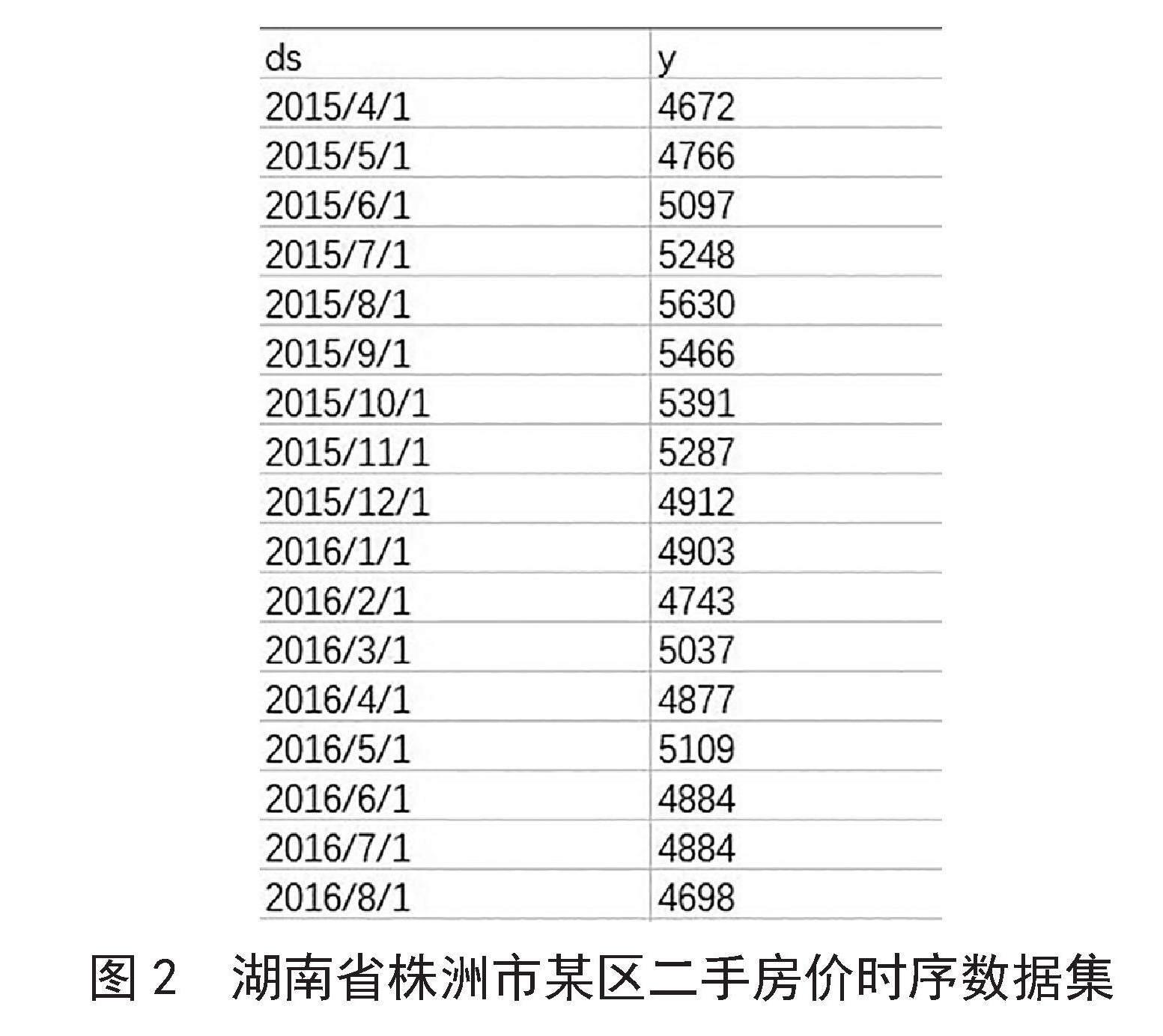
本文中的二手房价数据选取湖南省株洲市某区二手房价时序数据集进行预测实验，该时间序列数据集从2015年4月到2022年12月共有154个样本，部分数据如图2所示。

图2  湖南省株洲市某区二手房价时序数据集

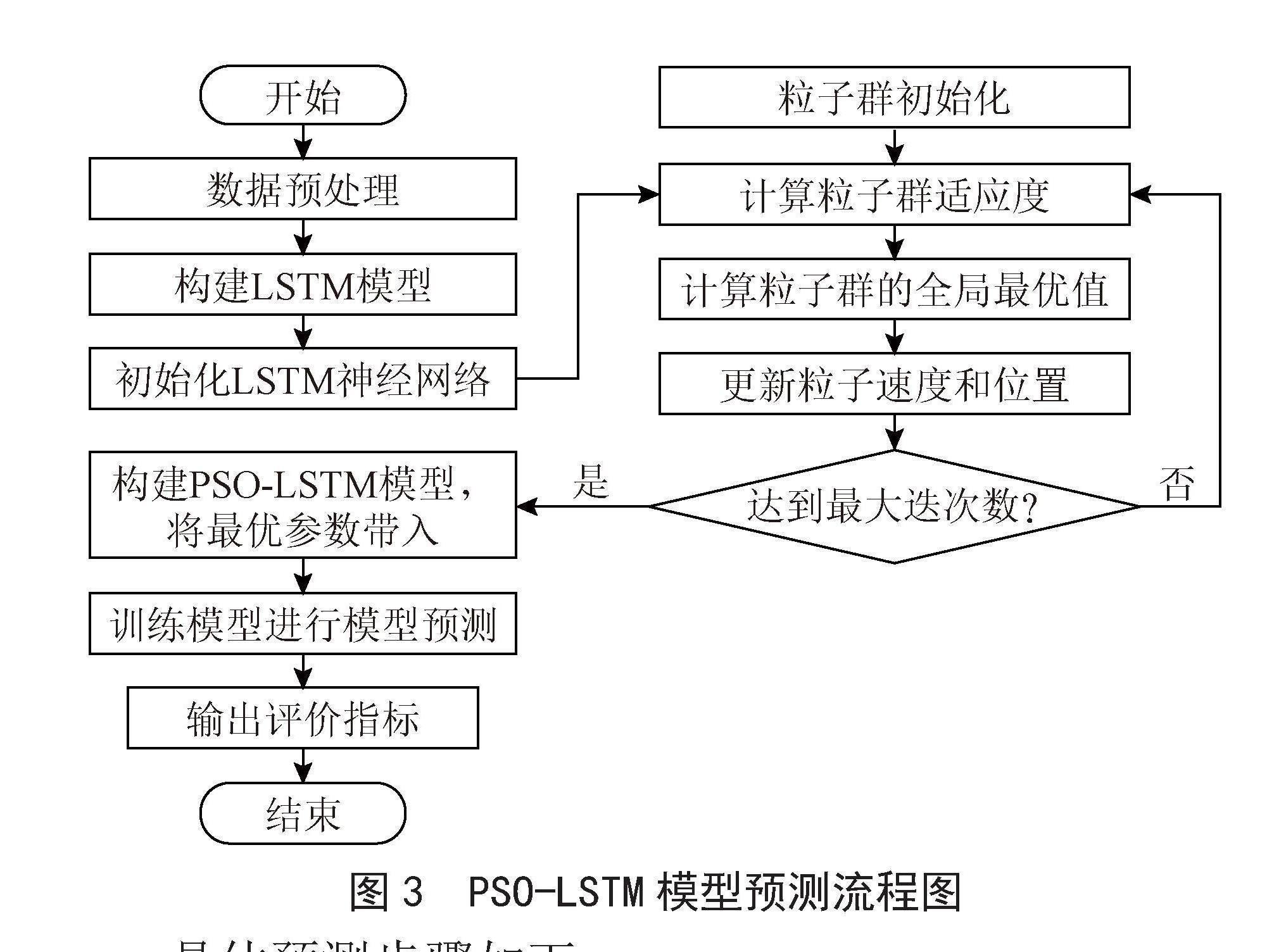
2.2  PSO-LSTM优化方法预测流程

LSTM神经网络虽然解决了时间序列数据的梯度爆炸和依赖问题，但是在面对大量的数据集时，在最优参数的选择上仍存在问题，不同的参数对于实验结果存在很大的误差。针对上述问题，本文通过采用PSO算法对LSTM神经网络进行优化，获得组合模型PSO-LSTM对区域二手房价进行预测，模型框架图如图3所示。

图3  PSO-LSTM模型预测流程图

具體预测步骤如下：

1）获取湖南省株洲市某区二手房价原始数据，并对数据进行预处理。通过对原始数据采用X12方法并结合EViews软件进行季节性因素的消除，如图4所示，再通过归一化等方法处理；接着对新得到的时序数据集进行划分，将新的时序数据集分为训练集和测试集，将前81条数据作为训练集，后12条数据作为测试集。

图4  EViews_X12方法图

数据归一化：本文通过最大最小标准化方法（Min-Max Normalization）进行归一化处理，将数据缩放到[0，1]的范围内，使得原始数据得到一个标准且变化平滑的数据集，计算方式如式（6）所示：

（6）

将归一化后的数据集分为训练集和验证集，通过Adam算法更新模型的权重和偏差，经过反复训练进而调整模型的超参数。得到预测结果后，需将预测结果进行反标准化处理，将缩放的预测值转换回原始的房价范围，从而与原始值进行对比。

2）初始化LSTM模型，本文采用LSTM标准的三层模型结构：输入层、LSTM层和输出层。初始化各参数值，构建LSTM神经网络模型，包括迭代数、批处理数、神经元个数等参数。采用ReLU函数作为隐藏层的激活函数，进而应用Adam优化器对模型整体进行优化处理，使其具备更有效的调整学习率的能力。这有助于优化模型训练过程，有效预防梯度爆炸问题的发生。

3）采用PSO算法对LSTM进行参数优化，粒子通过前一个粒子的最优位置，不断地进行位置和速度的更替，而空间范围内所有的粒子又同步向最优位置的粒子进行追踪，进而不断更新粒子的位置和速度，从而得到全局最优位置，通过全局寻优计算出最优粒子，从而得到LSTM的最优参数，提高预测模型的准确度。

4）将PSO得到的最优参数带入LSTM模型，其中迭代次数150，隐藏元120，学习率0.04。模型使用区域二手房价数据进行学习，通过LSTM神经网络深入分析时序数据，挖掘其中的潜在趋势以预测第1时间步的房价价格。在预测第2时间步时，通过调整滑动窗口，将第1时间步的预测房价价格加入训练集，以训练模型预测第2时间步的房价价格。随后，循环此过程，预测至第n时间步后停止。对输出的预测值进行反归一化的处理，得到最終的预测结果。

5）模型验证输出评价指标，采用RMSE和MAPE进行预测评估。两者评估值越小，代表PSO-LSTM模型的性能就越好。

2.3  实验环境

本文的实验采用64位的Win 10系统，处理器为AMD Ryzen 5 2500U with Radeon Vega Mobile Gfx，主频2.00 GHz，内存8 GB，在Python3环境下通过Jupyter Notebook实现全部实验过程。

2.4  PSO-LSTM模型拟合效果分析

在时序预测领域中，由于传统的神经网络预测存在梯度爆炸、梯度消失等问题，从而导致训练难度大，而LSTM神经网络模型的出现，改善了这一情况。因此，本文在模型的对比分析中采用LSTM模型与PSO-LSTM模型作为比对组，预测结果如图5所示。

图5  各预测数据拟合图

由图可看出PSO-LSTM模型的模型拟合度比LSTM神经网络模型的模型拟合度更接近实际值。且在2022年5月份的转折处，PSO-LSTM模型的值更贴近于实际值。LSTM模型的整体预测趋势与实际值的整体趋势有偏离，而PSO-LSTM模型的整体趋势更优于LSTM模型，更符合二手房价实际的趋势走向，很好地提升了预测精度。

3  实验结果与分析

本文采用预测评估公式RMSE和MAPE来对模型的预测结果进行计算并预测评估，在对PSO-LSTM和LSTM模型的预测数据进行评估后得到的数据值，RMSE和MAPE的评估值越小，则代表模型的性能就越好。从预测训练结果对比表表1中可看到，PSO-LSTM模型的RMSE值为137.28，相较LSTM降低了19.5%；而PSO-LSTM模型的MAPE值仅为1.59，比LSTM模型降低了22.05%。由评估预测值证实了PSO-LSTM模型的预测效果要优于LSTM模型。

表1  模型预测训练结果对比

预测模型 类别 RMSE MAPE

LSTM 时间序列模型 170.54 2.04

PSO-LSTM 神经网络 137.28 1.59

由实验结果证实了：通过PSO算法对LSTM模型进行优化可以很好地提升预测的精度，且优化后的模型能更好地适应大量的数据训练，使得预测的精度大大提升，对实际数据的曲线拟合效果好。相较LSTM神经网络模型，对真实数据的拟合效果更好，且预测评估也优秀。从上述评估角度可得出，PSO-LSTM模型对于区域二手房价的预测有更好的预测精度，能够给买家、金融业、房地产业等提供更为可靠和科学的二手房价预测。

4  结  论

为了提升区域二手房价的预测精度，消除影响因素，达到更好的拟合趋势，本文提出了一种基于PSO-LSTM的区域二手房价预测方法，通过引入PSO算法对LSTM模型进行优化，从而实现预测精度的提升。通过与LSTM神经网络模型的实验对比分析，PSO-LSTM模型预测方法能更好地对金融业、房地产业等产业进行高精度的预测，提供了合理且科学的预测参考。本文对PSO-LSTM的预测方法相较LSTM模型取得了更好的效果，预测精度也有提升，但对于整体的预测来说，并不能达到理想的预期。后续拟尝试新的算法结合本文中基于LSTM的区域二手房价预测方法进行创新，通过多因素变量的分析，进一步提升区域二手房价的预测精度。

参考文献：

[1] 王英伟，马树才.基于ARIMA和LSTM混合模型的时间序列预测 [J].计算机应用与软件，2021，38（2）：291-298.

[2] 陈孝文，苏攀，吴彬溶，等.基于改进长短期记忆网络的时间序列预测研究 [J].武汉理工大学学报：信息与管理工程版，2022，44（3）：487-494+499.

[3] 蔡兆晖，曾凯，陈秋强.结合集合经验模态分解的LSTM神经网络在大宗商品价格预测应用研究 [J].冶金经济与管理，2023（4）：52-56.

[4] 许钰林，康孟珍，王秀娟，等.基于深度学习的玉米和大豆期货价格智能预测 [J].智慧农业：中英文，2022，4（4）：156-163.

[5] 程先龙，保佑智，何度江，等.基于EMD-ELM-LSTM的短期风电功率预测 [J].昆明理工大学学报：自然科学版，2023，48（6）：78-87.

[6] 方雪清，吴春胤，俞守华，等.基于EEMD-LSTM的农产品价格短期预测模型研究 [J].中国管理科学，2021，29（11）：68-77.

[7] 高华睿，郝龙，王明明，等.基于Att-Bi-LSTM的高速公路短时交通流预测研究 [J].武汉理工大学学报，2020，42（9）：59-64.

[8] 于家斌，尚方方，王小艺，等.基于遗传算法改进的一阶滞后滤波和长短期记忆网络的蓝藻水华预测方法 [J].计算机应用，2018，38（7）：2119-2123+2135.

[9] 满建峰，侯磊，杨凯，等.基于PSO-LSTM混合模型的天然气管道多用气节点负荷预测研究 [J].油气与新能源，2022，34（6）：91-100.

[10] 高海翔，胡瑜，余乐安.基于分解集成的LSTM神经网络模型的油价预测 [J].计算机应用与软件，2021，38（10）：78-83.

[11] 吕柏行，郭志光，赵韦皓，等.标准粒子群算法的优化方式综述 [J].科学技术创新，2021（28）：33-37.

作者简介：周昌堉（1996—），男，汉族，广东汕头人，硕士研究生在读，研究方向：数据分析、智能信息处理；李长云（1971—），男，汉族，湖南衡阳人，教授，博士，研究方向：软件理论、物联网工程、人工智能。