基于改进MOEAD算法的主从式PID控制器参数寻优

胡鹰 吕畅 原嘉辰

摘 要：为了有效解决电液伺服系统主从控制结构中主缸和从缸PID控制器的参数设定问题，提出了一种基于多目标优化算法与模型仿真相结合的求解方法。在该求解方法中，将参数设定问题建模为了一个多目标优化问题，其目标空间包括主从同步误差、调节时间、超调量和积分平方误差四个维度，建立了主从结构的PID控制仿真模型，来获取目标空间的目标值。改进了MOEAD算法，通过亲代选择以及子代生成算子选择强化算法子代的多样性，通过个体与权重向量的绑定机制和外部种群对无效权重向量的替换策略对原始算法中的权重向量进行重调整。由改进的MOEAD算法获取了最终的Pareto非支配解集，在最终解集中选取了拐点个体作为控制器的最优参数，提高了主从同步结构的控制品质。

关键词：同步控制；多目标优化；仿真；PID控制

中图分类号：TP273   文献标志码：A    文章编号：1001-3695（2024）05-022-1434-07

doi： 10.19734/j.issn.1001-3695.2023.09.0400

Parameter optimization of master-slave PID controller based on improved MOEAD algorithm

Abstract：To solve the parameter tunning problem of PID controllers in master-slave control structure of electro-hydraulic servo system， this paper proposed a solution method based on multi-objective optimization algorithm combined with model simulation. This method modeled the problem as a multi-objective optimization problem whose target space included four dimensions， namely master-slave synchronization error， settling time， overshoot and integral squared error. And it established the simulation model of master-slave PID control structure to obtain the target value of the target space. Additionally， it improved the MOEAD algorithm by strengthenning the diversity of generated offspring through the selection of parents along with the offspring generate operators and readjusting the weight vector through the substitution strategy of invalid ones using external populations and binding mechanism between weight vectors and individuals. Finally， this method got the final Pareto non-dominated solution set and then selected the knee point individual as the optimal parameter of the controller in the solution set， which improves the control quality of the master-slave synchronization structure.

Key words：synchronous control; multi objective optimization; simulation; PID control

0 引言

液压传动技术因其具有的输出功率大、安装灵活、稳定可靠等优点，广泛应用于航空航天、海洋开发、土建工程等工业领域。在大多数设备中，往往要求两个或多个元件同步执行，这就需要对多套液压进行同步控制。同步控制系统包括等同式和主从式两种。等同式控制结构中，两个液压缸的参考值同时由外部提供，双缸之间无耦合关系，他们各自形成控制闭环。不同于等同式控制结构，在主从控制结构中，主缸接收外部的参考值，从缸接收主缸的实时输出值作为其参考值，即从缸跟随主缸的运动。主从缸的PID控制器参数需要分别给定。这种主从控制结构中，在满足PID控制的超调量、调节时间、调节误差等目标之外，还需要尽量减小主从缸之间的位移误差。而这种大时滞、非线性、强耦合系统的PID参数整定十分困难。

早期的PID整定方法为Z-N法［1］，由两位仪器公司的工程师提出，他们通过系统临界振荡时的增益和振荡周期计算出PID控制器参数。进化算法出现之后，很多研究人员将其用于PID控制器的参数整定。

一部分学者将单组PID控制器的整定问题建模为单目标优化问题，并使用单目标优化算法进行求解。Feleke等人［2］使用ITAE建立目标，并使用差分进化算法应用于能源系统的PID控制器。卢艳军等人［3］通过将PSO算法中的惯性权重做非线性动态下降处理，提高了算法的搜索性能，同時使用ITAE作为单目标，将算法应用于无人机PID控制器整定。吕红芳等人［4］将免疫思想引入PSO算法中，提高了算法精度，并使用ITAE作为单目标，通过对比实验证明改进后的粒子群算法控制效果更佳。上述研究人员将单组PID控制器的整定问题建模为单目标问题模型，并使用单目标优化算法进行求解。为了兼顾PID控制中的系统误差和收敛速度，文献多使用ITAE做目标函数。但ITAE指标倾向于选择调节时间较短的PID参数，在超调方面表现较差。其他的ISE、IAE等指标均表现出不同的响应特点，均不能得到PID控制器的最佳参数。

另一些学者采用加权和的方法处理PID控制器参数优化问题中的多个子目标。Sibtain等人［5］将光伏与风电网PID控制器的三项子目标做权重和，并将其对时间的积分作为单目标，使用GA进行整定。Goud等人［6］将连续搅拌釜式反器的PID控制器调节问题中的多个目标加权为一个目标，并用PSO进行优化。Ma等人［7］使用调节时间、输出偏差和系统输出三项的加权积分值作为单目标，并将改进后的差分进化算法应用于挖机电液伺服系统的PID参数优化。加权和可以将PID整定问题中多个子目标转换为单目标优化问题，从而使用单目标优化算法求解，但整定问题中，超调、调节时间和系统误差三个目标相互矛盾，它们之间的加权权重无法确定，导致求解结果不稳定。

还有一部分学者为PID的整定问题建立了多目标问题模型，并使用多目标优化算法进行求解。Milainovic＇等人［8］使用NSGA-Ⅱ来调节水文预测工具中的PID控制器，建立了一系列的二维目标函数组，并对各组目标函数进行了测试。Liu等人［9］为PID参数调节问题设置了直接目标和非直接目标，并建立了对应的多目标优化问题模型进行求解。Sabahi等人［10］将模糊PID的整定建模为两目标优化问题，并使用AWPSO（adaptive weighted PSO）算法求解。Rajamani等人［11］为硬件电路设计问题中的PID控制器整定问题建立了目标空间为两维的多目标优化问题模型，并使用NSGA-Ⅱ来进行求解。在这部分文献中，同样只对单组PID控制器的整定问题进行求解。这些文献中仅将PID控制器整定问题建立为目标空间两维的多目标优化问题，未能有效处理问题中其他控制指标。

本文将主从控制结构的液压缸同步控制系统PID控制器参数整定问题建模为目标空间四维、决策空间六维的多目标优化问题。在目前相关文献中，常用且较为成熟的求解算法包括GA［12］、PSO［13］、DE［14］和NSGA-Ⅱ［15］等。GA模拟自然进化过程对问题进行求解，作为一种随机搜索算法，其适用于任意形式的目标函数，但其搜索能力较差。PSO算法受鸟群捕食行为启发而来，算法使用群体最优信息与个体最优信息来引导种群迭代，因此其收敛速度较GA快，但易早熟收敛，且无法保证获取全局最优解。DE基于个体间差向量做变异操作，算法参数少，原理简单，鲁棒性强，但仍易落入局部最优。GA、PSO和DE同属于单目标优化算法，不适用于本文的多目标问题模型。NSGA-Ⅱ是多目标优化算法NSGA的改进版，加入了精英策略与拥挤距离，提高了原算法的性能，但随着目标数量增多，非支配排序的选择压力逐渐不足，因此仅适用于三个目标或以下的优化问题。MOEAD算法［16］基于权重向量分解生成子问题，天然具有更好的搜索能力，且其选择压力强于NSGA-Ⅱ，算法复杂度低于NSGA-Ⅱ。本文选择MOEAD算法进行求解，通过对MOEAD算法的改进，加强其获取复杂帕累托前沿的能力。将改进后的多目标优化算法应用于主从控制结构的PID控制器参数整定问题中。对比该方法与传统的Z-N法、经典单目标优化方法和经典多目标优化方法，验证了本文方法对主从结构PID控制器进行整定的可行性和有效性，具有一定的实际应用价值。

1 同步控制系统的控制结构

阀控液压缸的闭环同步控制有等同同步控制和主从同步控制两种控制策略。图1、2分别为两种控制策略下的PID控制框图。本文解决后者的PID控制器整定问题。

图中，PID控制器将给定参考值与实际输出值的偏差分别做比例（P）、积分（I）、微分（D），并将三个计算量线性组合为控制量，对被控对象进行控制。

2 多目标优化问题建模

使用MATLAB中的Simulink工具箱对主从模式的PID控制结构建模。以某型矫直机为例，其主压下系统采用主从同步控制结构。一组阀控液压缸的传递函数通过查阅文献［17］得到。由伺服阀阀芯位移到液压缸活塞位移的传递函数为

其中：Kh为伺服阀的增益；ωh为阀控液压缸系统固有频率；ξh为系统阻尼比。文献［17］给出了某型矫直机的一组参数，并依据设备参数计算得到了阀控液压缸传递函数中三个参数Kh、ωh、ξh的取值。具体取值情况见表1。

故，此阀控液压缸系统的传递函数为

使用Simulink建立的主从结构同步控制仿真模型中，PID模塊共有两个，分别对应主、从缸的控制器，共6个参数，分别对应主、从缸控制器的P、I、D值。

仿真模型的输出设定为对应时间序列的位移量。依据仿真模型来建立多目标优化的问题模型。

图3为仿真模型。图中1、2、3号输出端口为后续建立问题模型所使用，simout即为含有对应时间序列的位移量。

2.1 同步误差目标

使用同步误差建立目标函数，用式（3）来计算调节过程中主、从缸之间的位移累计误差。

其中：T为仿真模型的仿真时长；mt和st为对应时间标签t处的主缸和从缸位移值。

2.2 主、从缸的调节时间目标

当系统偏移量小于2%时，系统判定为稳定，计算此时的时间。计算方法如式（4）所示。

Tst=Tm_st+Ts_st（4）

其中：Tm_st和Ts_st分别为主、从缸的调节时间，计算方法由式（5）（6）来表示。

其中：sm_output为主缸位移值；rm为主缸接收的外部参考值；ss_output为从缸的位移值；rs（t）为从缸的参考值，从缸跟随主缸移动，它的参考值即为主缸的位移值，是时间t的函数。在偏差小于参考值的2%时判为稳定。

2.3 主、从缸的超调目标

超调量也叫最大偏差，表示被控量偏离参考值的程度，这项指标在实际工程中十分重要，使用式（7）进行计算。

σ=σm+σs（7）

式（7）包括主缸超调部分σm和从缸超调部分σs，从缸参考值会随时间改变，因此，从缸的超调值取所有仿真时间标签中的最大值。主缸超调部分和从缸超调部分分别为

σm=max（sm_output（t）－rm）（8）

σs=max（|ss_output（t）－rs（t）|）（9）

其中，主缸超调计算时只考虑位移大于参考值的情况，从缸超调计算时考虑与其参考值偏差的绝对值。

2.4 主、从缸的积分平方误差目标

主缸和从缸的积分平方误差（ISE）计算式为

Fise=Fm_ise+Fs_ise=∫（|em（t）|2）dt+∫（|es（t）|2）dt（10）

包含了一组PID控制中，控制量与参考值的偏差。其中：Fm_ise为主缸积分平方误差；Fs_ise为从缸积分平方误差；e（t）为时刻t时的位移值与参考值之间误差，t为仿真时间。

综上所述，建立多目标优化问题模型。其目标空间为四维，决策空间为六维。问题模型的描述如式（11）所示，式中决策向量为主从两组PID控制器的参数，每组为三个。目标向量由四个目标值组成，分别为同步误差、调节时间、超调量和积分平方误差。

min y=f（x）=［Fsyc，Tst，σ，Fise］

x=［xm_p，xm_i，xm_d，xs_p，xs_i，xs_d］

s.t.  xmin≤x≤xmax（11）

3 MOEAD多目标优化算法的改进

真实世界的优化问题不同于测试函数，它的Pareto前沿未知。这就要求算法能够有效处理各种复杂的Pareto前沿面。MOEAD算法的三种分解方法中，基于切比雪夫的分解法对凸和非凸问题均表现较好，本文基于此分解法进行改进。传统的MOEAD算法在面对降维、不连续、非凸等的复杂Pareto前沿时，存在不能找到所有Pareto前沿、处理结果依赖超参数、易落入局部最优等问题。为了解决这些问题，本文提出基于权重向量重调整的改进MOEAD算法，即MOEAD-WDN（weighted vector dynamic readjust based on non-dominated external population）。

3.1 子代的生成

为了增强子代个体的多样性，依概率p在邻居内或在全部个体中随机选取亲本，算法中p取0.8。如式（12）所示，i为种群中个体的序号，T为个体的邻域范围，mi为个体i的配对池，population为全体种群。

在确定配对池后，依概率选择GA算子或选择DE算子生成子代。依次遍历种群中的个体后，得到子代种群offspring。如式（13）所示，r为0～1的随机数，在本文算法中，q取0.5。

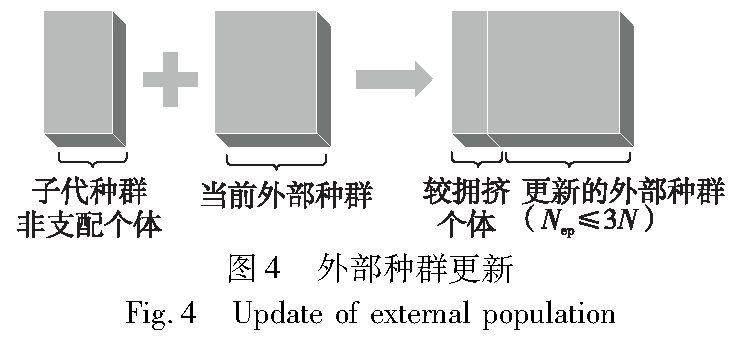
3.2 外部种群的更新

如图4所示，子代全部生成后形成的子代种群将与当前的外部种群合并形成新的外部种群EP，对合并形成的EP非支配排序，并取得其非支配解，取非支配解集作为最终的外部种群EP。外部种群更新如图4所示。

随着迭代的进行，子代种群offspring中的非支配解会越来越多，为了减小计算的开销，限制外部种群EP的数量上限为三倍的种群数量。当外部种群EP中的个体过多时，计算其中个体的拥挤程度，并去掉较拥挤的个体，使外部种群个体数量维持在种群个体数量的三倍。

3.3 无效权重向量的判定

执行切比雪夫分解，并进行邻域更新，被更新的邻居个体上限设为邻域个体数量的30%。形成当前的种群后，对当前种群进行非支配排序，得到非支配解。为了增强算法的探索能力，改进的算法中，将权重向量与种群中的非支配解按照余弦距离最近原则进行严格的一对一绑定。一个权重向量只能与一个距离自己最近的非支配解绑定，同时，一个非支配解只能绑定在一个权重向量上。当非支配解与权重向量绑定完成后，一部分权重向量未参与绑定。未绑定的权重向量即为当前迭代中的失效权重向量。依据失效权重向量拥挤程度对其进行排序。采用邻近距离作为拥挤度量，计算方法如式（14）所示，其中：m为目标空间维度，dis为离第j个wv最近的第i个wv的距离。标记失效权重向量中较为拥挤的前8%，在下一步中对其重调整。

如图5所示，以两目标情况下的算法为例， f1和f2为所优化问題的两个目标，假设a～f为当前目标空间存在的6个权重向量，1～4为当前种群对应的目标空间的点，它们是非支配的。权重向量a与点1绑定，距离权重向量b较近的有两个点，分别为点2和点3，但b已经与点2绑定，所以点3只能与距离其较近的下一个权重向量c绑定。点4距离权重向量e较近且e未参与绑定，所以将点4与权重向量e绑定。在绑定完成后，权重向量d、f即为本次判定得到的无效权重向量。

3.4 无效权重向量的调整

取出种群中与无效权重向量对应的个体，并从权重向量集合中去除失效权重向量。使用外部种群EP中的个体对去掉的个体和权重向量进行补全。

依次选择距离种群最远的外部种群中的个体对当前种群进行补全，同时将个体的坐标映射到目标空间的单位超平面上，建立对应的权重向量，补全权重向量集合。依次执行上述步骤，直到种群数量恢复至原有。

如图6所示，D为目标空间的单位超平面，二维情况下单位超平面为一条线。在上一步去除无效权重向量d、f后，目标空间仅剩a、b、c、e四个权重向量，需从外部种群中取个体对当前权重向量和当前种群进行补全。点5和6为外部种群中距离当前种群较远的点，将它们补进当前种群，并根据其在单位超平面上的映射点建立权重向量g和h。此时权重向量数量和个体数量又恢复至初始情况。而无效权重向量d、f被替换为权重向量g、h。

随后判断是否满足算法停止条件，若不满足，则使用此时形成的种群进行下一次的迭代，当满足条件后，输出此时的种群作为最终种群。

在解决真实世界问题时，需要在获取的最终种群中提取最终个体。由于在拐点附近，一个目标值的少量提升会造成其他一个或多个目标值的显著下降，所以这个具有最大边际效用的点常被认为是最具吸引力的点。本文取拐点作为最终个体。获取到最终种群后，对目标空间个体归一化，计算由极值构成的超平面，并计算距离此超平面最远的点，即为拐点。

如图7所示，以目标空间三维为例，图中圆点为算法运行结束后目标空间得到的最终点集，此时建立超平面D，并计算各点到D的距离，取距离最大的点3作为拐点。

拐点在決策空间对应的个体即为最终决策向量。决策向量前三位元素为系统主PID控制器参数，后三位元素即为系统从PID控制器参数。改进后的MOEAD算法流程如图8所示。算法结束条件设为10 000次评价次数。

4 算法的有效性验证

本文算法运行环境主要为Intel Core i5-8400、2.8 GHz CPU、8 GB RAM、64 bit Windows10系统的PC机。算法采用MATLAB编程，版本为2021b，使用基于MATLAB的多目标优化算法测试平台PlatEMO［18］进行测试，PlatEMO平台版本为3.5。

4.1 测试函数及指标

使用典型多目标优化测试问题系列IMOP［19］。IMOP测试函数系列共包含八个测试函数，其中，IMOP1、IMOP2和IMOP3为二维问题，其余为三维问题。IMOP1和IMOP2的Pareto前沿分别为具有尖尾的一维凸曲线和一维非凸曲线。对进化算法来说，非凸问题较难求解，尖尾部分的解通常较难获得。IMOP3的Pareto为一维不连续曲线。IMOP4是在三维空间中的一条波浪线，代表了多目标优化问题中的降维问题。IMOP5为三维空间中不连续的8个圆面。IMOP6为空间中的网格平面，IMOP7为空间中球体非凸的一部分。IMOP8则包含了100个不连续的小区域，每个子区域由离散的点组成。图9为IMOP测试集的8种Pareto前沿面。为了有效对比各个算法的测试结果，使用反转世代距离指标IGD［20］和超体积指标HV［21］作为评价标准。

反转世代距离是一个综合性能评价指标，它计算每个在真实Pareto上的点到算法获取的个体集合之间的最小距离和，其值越小，代表着算法的收敛性和分布性越好。IGD的计算方法如式（15）所示。

其中：P为测试函数的Pareto面上均匀分布的点集；|P|为Pareto前沿面上点的个数；Q为算法获取的最优Pareto最优解集；d（v，Q）为P中的个体到Q中点集的最小欧氏距离。当算法性能较好时，IGD指标会相对较小；当性能较差时，算法获取的最优解集会汇聚在局部区域，解集中的点距离真实Pareto会较远，使得IGD指标偏大。

另一项评价指标超体积HV的计算方法如式（16）所示。

在HV计算式中，P为与测试函数的真实Pareto对应的参考点集，通常为多个目标上的最大值形成的向量。当算法性能较优时，超体积更大。

4.2 与其他多目标算法的对比

取近年来的六个多目标优化算法与MOEAD-WDN进行对比。分别为：DEAGNG［22］、TiGE2［23］、PREA［24］、NSGAⅡSDR［25］、MOEADVOV［26］、DEGA［27］。对比算法的参数设置为其推荐值，如表2所示。每个算法在每项测试函数上均独立进行20次测试，最终采用Wilcoxon秩和检验以0.05的显著性水平来比较各个算法的性能。当p值小于0.05则拒绝原假设，说明作为对比对象的两个算法存在显著差异，否则说明对比对象的相差不大。

在IMOP测试函数系列上的结果见表3、4。“+”表示算法优于比较对象，“-”表示算法劣于比较对象，而“=”则表示算法与比较对象没有统计意义上的显著差异。测试中的种群数量设为100，最大评价次数设为10 000。在表3、4中，较优结果已用加粗字体表示。由结果可知，在IGD指标方面，本文算法仅在IMOP1上与最优方法有小幅差距。在HV指标指标方面，MOEAD-WDN仅在IMOP8上与最优算法有少许差距，在其他7个测试函数上均占优。结果表明，MOEAD-WDN算法可以有效得到各种特殊的Pareto前沿，且算法综合性能优于六个比较对象。

5 仿真与对比实验

5.1 仿真条件设置

对主从控制结构的PID系统施以单位阶跃激励。其他仿真条件包括仿真时间、种群规模、评价次数，取值见表5。

5.2 仿真与结果分析

将本文方法与其他传统PID整定方法进行对比。用作对比的方法包括Z-N、GA、PSO、NSGA-Ⅲ和MOEAD算法。Z-N中主从缸控制器取同一组PID参数。由于本文问题模型目标空间为四维，所以使用适用于超多目标的升级版算法NSGA-Ⅲ作为对比。得到的PID参数见表6。

GA和PSO均属于单目标优化法，在这些方法中，使用主从缸各自的积分平方误差、超调、调节时间以及主从缸同步误差七个目标取权重1组成加权目标。NSGA-Ⅲ、MOEAD和本文方法均属于多目标优化方法。这些方法的仿真使用本文提出的多目标优化问题模型。将取得的六组PID控制参数分别代入仿真模型，得到响应曲线后，计算控制质量指标，结果见表7。

表7中各项指标的最优值均以粗体表示，最劣值均以下画线标出。在同步控制的各项控制指标中，同步误差是其中的关键指标。其结果对比如图10所示。

由图10可知，三种多目标优化方法得到的主从同步误差均远小于Z-N和单目标法。其中MOEAD最差，NSGA-Ⅲ最优。

各种方法得到的主从缸调节时间对比结果如图11所示，超调指标和ISE指标的对比结果分别如图12、13所示。

如图11所示，NSGA-Ⅲ取得的主缸调节时间远远大于其他方法，它对主缸的调节时间超过了3 s，这在现场作业中不可接受。其他各方法调节时间均低于0.5 s。

超调方面，如图12所示，Z-N的主、从缸超调值远高于其他，而NSGA-Ⅲ最低。在ISE指标方面，如图13所示，NSGA-Ⅲ的主缸数值要远高于其他方法，其他方法均在0.05以内。综合考虑上述各项指标，三种多目标优化方法在关键的同步误差指标方面优于Z-N和单目标优化方法。多目标优化方法中的NSGA-Ⅲ虽然在同步误差方面优于本文方法，但其调节时间、ISE指标在六种方法中最差，且主缸调节时间过长。本文方法的同步误差仅有MOEAD方法的一半，而在其他方面均无明显差距。对比实验的结果证明本文方法较优。

6 結束语

液压同步机构有等同式和主从式两种控制结构，其中的主从式控制结构存在非线性、强耦合、大延迟的特点。主、从缸的PID控制器参数难以找到最优值。为解决此问题，本文将其建模为目标空间四维、决策空间六维的多目标优化问题。分别围绕控制质量指标要求中的超调量、调节时间、调节误差以及同步控制中要求的同步误差建立四个目标函数。在处理真实世界多目标优化问题时，由于Pareto前沿面未知，传统多目标优化算法对这种情况的处理不理想。本文以MOEAD算法为框架，提出基于失效权重向量的判定与重调整的改进算法MOEAD-WDN，增强了算法对未知Pareto前沿面的逼近能力，使算法能更有效地处理具有退化、不连续、非凸等特殊Pareto前沿的问题。通过与其他PID调节方法对比，证明了本文方法的先进性，有效提高了主从同步控制结构PID控制器的控制品质。

参考文献：

［1］敖翔，王黎明，汪洋，等. 基于齐格勒-尼柯尔斯PID算法对车辆纵向行驶稳定性的研究［J］. 车辆与动力技术，2022（4）： 21-26，37. （Ao Xiang，Wang Liming，Wang Yang，et al. Research on vehicle longitudinal driving stability based on Ziegler-Nichols PID algorithm［J］. Vehicle & Power Technology，2022（4）： 21-26，37.）

［2］Feleke S，Satish R，Tatek W，et al. DE-algorithm-optimized fuzzy-PID controller for AGC of integrated multi area power system with HVDC link［J］. Energies，2022，15（17）： 6174.

［3］卢艳军，郭竟翔，李忠海. 基于改进粒子群优化的旋翼无人机PID参数整定算法［J］. 探测与控制学报，2022，44（5）： 116-124. （Lu Yanjun，Guo Jingxiang，Li Zhonghai. Rotor UAV PID parameter tuning algorithm based on improved particle swarm optimization［J］. Journal of Detection and Control，2022，44（5）： 116-124.）

［4］吕红芳，王涛，嵇月强，等. 基于免疫粒子群算法的PID参数优化研究［J］. 中国工程机械学报，2022，20（3）： 194-198. （Lyu Hongfang，Wang Tao，Ji Yueqiang，et al. Research on PID parameter optimization based on immune particle swarm algorithm［J］. Chinese Journal of Construction Machinery，2022，20（3）： 194-198.）

［5］Sibtain D，Murtaza A F，Ahmed N，et al. Multi control adaptive fractional order PID control approach for PV/wind connected grid system［J］. International Trans on Electrical Energy Systems，2021，31（4）： e12809.

［6］Goud H，Sharma P C，Nisar K，et al. PSO based multi-objective approach for controlling PID controller［J］. Computers，Materials & Continua，2022，71（3）： 4409-4423.

［7］Ma Wei，Ma Shoulei，Qiao Wenhua，et al. Research on PID controller of excavator electro-hydraulic system based on improved differential evolution［J］. Machines，2023，11（2）： 143.

［8］Milainovic＇ M，Prodanovic＇ D，Stanic＇ M，et al. Control theory-based data assimilation for open channel hydraulic models： tuning PID controllers using multi-objective optimization［J］. Journal of Hydroinformatics，2022，24（4）： 898-916.

［9］Liu Liheng，Yan Jin，Wang Jinping，et al. Multi-objective optimization of PID controller of outlet temperature of DSG trough solar collector［J］. Energy Reports，2021，7： 479-493.

［10］Sabahi K，Zhang Chunwei，Kausar N，et al. Input-output scaling factors tuning of type-2 fuzzy PID controller using multi-objective optimization technique［J］. Energy，2023，8（4）： 7917-7932.

［11］Rajamani M，Rajesh R，Iruthayarajan M W. Design and experimental validation of PID controller for buck converter： a multi-objective evolutionary algorithms based approach［J］. IETE Journal of Research，2023，69（1）： 21-32.

［12］王永，呂致为. 基于基因库求解旅行商问题的遗传算法［J］. 计算机应用研究，2023，40（11）： 3262-3268. （Wang Yong，Lyu Zhiwei. Genetic algorithm for solving thetraveling salesman problem based on gene library［J］. Application Research of Computers，2023，40（11）： 3262-3268.）

［13］谢美华，李艳武，葛棚丹. 自适应混合粒子群算法求解置换流水车间调度问题［J］. 计算机应用研究，2023，40（11）： 3241-3246，3253. （Xie Meihua，Li Yanwu，Ge Pengdan. Self-adaptive hybrid particle swarm optimization for permutation flow shop scheduling problem［J］. Application Research of Computers，2023，40（11）： 3241-3246，3253.）

［14］Wang Peng，Xue Bing，Liang Jing，et al. Differential evolution-based feature selection： a niching-based multiobjective approach［J］. IEEE Trans on Evolutionary Computation，2022，27（2）： 296-310.

［15］陈龙，刘勤明，叶春明，等. 基于改进的NSGA2算法考虑病患公平性及医院运作成本的病床配置优化研究［J］. 计算机应用研究，2022，39（8）： 2414-2421，2431. （Chen Long，Liu Qinming，Ye Chunming，et al. Research on hospital bed allocation optimization considering patient fairness and hospital operating costs based on the improved NSGA2 algorithm［J］. Application Research of Compu-ters，2022，39（8）： 2414-2421，2431.）

［16］Chang Yatong，Luo Wenjian，Lin Xin，et al. Multiparty multiobjective optimization by MOEA/D［C］//Proc of IEEE Congress on Evolutio-nary Computation. Piscataway，NJ： IEEE Press，2022： 01-08.

［17］陈聪. 电液伺服系统特性分析与滑模变结构控制器设计［D］. 太原： 太原科技大学，2014. （Chen Cong. Characteristic analysis of electro-hydraulic servo system and design of sliding mode variable structure controller［D］. Taiyuan： Taiyuan University of Science and Technology，2014.）

［18］Tian Ye，Cheng Ran，Zhang Xingyi，et al. PlatEMO： a MATLAB platform for evolutionary multi-objective optimization ［educational forum］ ［J］. IEEE Computational Intelligence Magazine，2017，12（4）： 73-87.

［19］Tian Ye，Cheng Ran，Zhang Xingyi，et al. Diversity assessment of multi-objective evolutionary algorithms： performance metric and benchmark problems ［research frontier］ ［J］. IEEE Computational Intelligence Magazine，2019，14（3）： 61-74.

［20］Wang Zihan，Xiao Chunyun，Zhou Aimin. An exact inverted generational distance for continuous pareto front［C］// Proc of International Conference on Parallel Problem Solving from Nature. Cham： Sprin-ger，2022： 96-109.

［21］Riquelme N，Von Lücken C，Baran B. Performance metrics in multi-objective optimization［C］// Proc of Latin American Computing Conference. Piscataway，NJ： IEEE Press，2015： 1-11.

［22］Liu Yiping，Ishibuchi H，Masuyama N，et al. Adapting reference vectors and scalarizing functions by growing neural gas to handle irregular Pareto fronts［J］. IEEE Trans on Evolutionary Computation，2019，24（3）： 439-453.

［23］Zhou Yalan，Zhu Min，Wang Jiahai，et al. Tri-goal evolution framework for constrained many-objective optimization［J］. IEEE Trans on Systems，Man，and Cybernetics： Systems，2018，50（8）： 3086-3099.

［24］Yuan Jiawei，Liu Hailin，Gu Fangqing，et al. Investigating the properties of indicators and an evolutionary many-objective algorithm using promising regions［J］. IEEE Trans on Evolutionary Computation，2020，25（1）： 75-86.

［25］Tian Ye，Cheng Ran，Zhang Xingyi，et al. A strengthened dominance relation considering convergence and diversity for evolutionary many-objective optimization［J］. IEEE Trans on Evolutionary Computation，2018，23（2）： 331-345.

［26］Takagi T，Takadama K，Sato H. Weight vector arrangement using virtual objective vectors in decomposition-based MOEA［C］// Proc of IEEE Congress on Evolutionary Computation. Piscataway，NJ： IEEE Press，2021： 1462-1469.

［27］He Cheng，Cheng Ran，Yazdani D. Adaptive offspring generation for evolutionary large-scale multiobjective optimization［J］. IEEE Trans on Systems，Man，and Cybernetics： Systems，2020，52（2）： 786-798.