一种基于梯度的多智能体元深度强化学习算法
赵春宇 赖俊 陈希亮 张人文
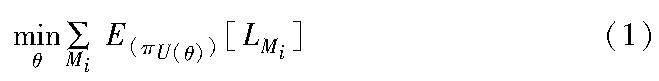
摘 要:多智能体系统在自动驾驶、智能物流、医疗协同等多个领域中广泛应用,然而由于技术进步和系统需求的增加,这些系统面临着规模庞大、复杂度高等挑战,常出现训练效率低和适应能力差等问题。为了解决这些问题,将基于梯度的元学习方法扩展到多智能体深度强化学习中,提出一种名为多智能体一阶元近端策略优化(MAMPPO)方法,用于学习多智能体系统的初始模型参数,从而为提高多智能体深度强化学习的性能提供新的视角。该方法充分利用多智能体强化学习过程中的经验数据,通过反复适应,找到在梯度下降方向上最敏感的参数并学习初始参数,使模型训练从最佳起点开始,有效提高了联合策略的决策效率,显著加快了策略变化的速度,面对新情况的适应速度显著加快。在星际争霸Ⅱ上的实验结果表明,MAMPPO方法显著提高了训练速度和适应能力,为后续提高多智能强化学习的训练效率和适应能力提供了一种新的解决方法。
关键词:元学习;深度强化学习;梯度下降;多智能体深度强化学习
中图分类号:TP181 文献标志码:A 文章编号:1001-3695(2024)05-011-1356-06
doi: 10.19734/j.issn.1001-3695.2023.09.0411
Gradient-based multi-agent meta deep reinforcement learning algorithm
Abstract:Multi-agent systems have a wide range of applications in many fields, such as autonomous driving, intelligent logistics, and medical collaboration, etc. However, due to technological advances and increased system requirements, these systems face challenges such as large scale and high complexity, and often suffer from inefficient training and poor adaptability. To address these problems, this paper proposed a multi-agent first-order meta proximal policy optimization (MAMPPO) method by extending gradient-based meta-learning to multi-agent deep reinforcement learning. The method learned the initial model parameters in the multi-agent system to provide a new perspective for improving the performance of multi-agent deep reinforcement learning. It made full use of the previous experience in the process of multi-agent reinforcement learning to find the most sensitive parameters in the direction of gradient descent through repeated adaptation, and learned the initial parameters so that the model training starts from the optimal starting point. This method effectively improved the decision-making efficiency of the joint policy, and led to a significant increase in the speed of its policy change, which significantly accelerated the speed of adaptation in the face of a new situation. Experimental results on StarCraft Ⅱ show that the MAMPPO method can significantly improve the training speed and adaptability, which provides a new solution for the subsequent improvement of the training efficiency and adaptability of multi-agent reinforcement learning.
Key words:meta learning; deep reinforcement learning; gradient descent; multi-agent deep reinforcement learning
0 引言
在單智能体强化学习(single-agent deep reinforcement learning,SARL)中,智能体与环境相互作用并作出有效决策以最大化累积收益。随着计算能力和存储容量的显著提高,任务的规模和复杂程度也进一步提高。为了有效解决一系列复杂问题,深度学习(deep learning, DL)和强化学习(reinforcement learning,RL) 成功结合产生了深度强化学习(deep reinforcement learning,DRL)。并展现了广泛的应用前景,如掌握围棋[1]、平流层气球导航[2]、大规模战略博弈[3]、机器人在挑战性地形中的移动[4]、3D打印[5]等。例如,Open AI Five在Dota 2 中首次击败人类冠军队伍[6],并在模拟的捉迷藏物理环境中成功训练出一个可以像人类一样使用工具的智能体[7]。
为了解决多智能体系统(multi-agent system,MAS)下的复杂决策问题,在MAS中引入了DRL的思想和算法,提高多智能体深度强化学习(multi-agent deep reinforcement learning,MADRL)的性能和效率,MADRL具有较强的决策和协调能力,是解决大规模复杂任务的重要方法。
元学习通过积累先前经验来快速适应新的任务,凭借“学习如何学习”的特性,在单智能体强化学习(SADRL)中得到了广泛应用,有效避免了巨大数据量和高复杂度的样本数据出现。基于梯度的元强化学习在学习过程中学习模型初始参数,使模型在每次学习任务时可以从一个最佳的起点开始,而不是像强化学习一样从零出发,有效提高了训练效率;因其初始参数是在训练任务上反复适应经多次梯度下降所得,该参数在梯度方向上与目标参数接近,所以训练好的模型在适应过程中仅需几步梯度下降步骤就可以达到目标参数,缩短了大量的适应时间。然而与SADRL相比,MADRL具有更多的智能体,更高的网络结构复杂性,并且在联合状态-行动空间中呈指数增长,这大大增加了探索的难度,致使其每次训练都要处理巨大的计算量和高复杂度的样本数据,延长了训练和适应速度[8]。
为了提高训练效率和适应能力,受单智能体元强化学习的启发,将基于梯度的元学习方法扩展到MAS,提出了一种名为多智能体一阶元近端策略优化(multi-agent first-order meta proximal policy optimization PPO, MAMPPO)的方法,旨在从有限的经验中不断学习和适应,该方法通过收集每个智能体与环境交互产生的经验数据,并将其划分为不同的任务数据块,通过任务数据块进行反复自适应和更新,充分利用先前经验,学习最接近目标模型的起始参数作为模型的初始化参数。这使得模型在新情况下只需几步的梯度下降就能达到目标,有效提高了MADRL的策略更新效率,面对新形势的适应速度显著加快。通过本文的研究和实验证明了MAMPPO方法在提高MADRL的速度泛化方面的有效性和效果,为改善多智能体系统中的决策问题提供了一种新的方法,并为进一步应用MADRL技术提供了有益的启示和指导。
1 相关工作
本文主要探讨了一种将MADRL与元学习相结合的方法,涉及到元深度强化学习、MADRL的相关研究工作以及多种成功的组合成果,本章对元强化学习和MADRL的相关工作进行介绍,讨论了各自领域中的重要研究成果和方法,并指出了它们在实践中的优点和局限性。
元学习因其“学习如何学习”的特性而被广泛应用于强化学习,通过利用先前任务中学到的经验和知识,智能体能够更快地适应新任务、更高效地利用数据、更准确地选择参数更新方向,并更好地平衡探索与利用。元强化学习旨在通过学习适应性算法或策略,使智能体能够从先前的经验中快速适应新任务。与传统的强化学习不同,元强化学习是一种学习输出策略的强化学习算法,通过数据驱动的方式来开发学习所需的训练环境和参数。
元强化学习假设存在相关任务的分布p(T),这对应于马尔可夫决策过程(MDP)M={Mi}Ni=1的分布,其中可以参数化MDP的动态或奖励。M由元组〈S,A,p,R,γ,ρ0,H〉定义,其中S为状态空间,A为行动空间,p为转移概率密度,R为奖励函数,H为事件的时间范围。元学习的目标是找到一组合适的参数集θ和配对更新方法U,使策略π在保持累积奖励最大的情况下解决新情况。设L(Mi)为Mi的损失函数,则元学习的目标可以表示为
本文的工作主要涉及基于梯度的元强化学习方法,该方法学习初始化模型参数使之在新任务上仅需微调,从而使训练好的模型能够适应新任务。Finn等人[9]提出了一种名为无模型元学习(model-agnostic meta-learning,MAML)方法,通过在梯度下降过程中寻找对更新方向敏感的模型参数,从而学习到适当的初始模型参数,实现了深度网络在快速适应任务上的能力增强;然而MAML方法在实际应用中仍面临一些挑战,如对任务表示的依赖性和计算复杂度有所增加。在MAML的基础上,Xu等人[10]提出了一种名为无模型元学习的元权重学习方法,在训练过程中对权重进行适应性更新,从而增强了神经网络的性能和泛化能力;然而该方法仍然面临一些挑战,如合理选择元学习率、网络结构的适应性以及计算复杂度的增加等。类似于MAML,Nichol等人[11]提出了一种称为一阶元学习(Reptile)的方法,通过在每个任务的训练后利用参数差异进行参数更新,从而实现了原始模型的快速適应,该方法在元学习的过程中避免了二阶导数的计算;然而仍面临一些挑战,如如何选择合适的学习率和对参数更新的限制等问题。Song等人[12]提出了一种名为ES-MAML的简单、不使用Hessian矩阵的元学习方法,该方法通过应用进化策略(ES)[13]来解决MAML中估计二阶导数的问题,在元学习过程中通过在目标函数中添加额外的探索项增加了探索的机会,以提供最大量的有用信息。为了选择合适的探索策略并平衡探索与利用之间的关系,Stadie等人[14]在元强化学习中考虑了学习探索策略,通过将额外的探索项添加到目标函数中,提出了一种名为学习探索的元强化学习方法,旨在增加探索的机会,以提供更多有用信息的数据量。Xu等人[15]提出了一种名为元策略梯度学习探索的方法,通过使用元策略梯度优化探索策略,使智能体能够学会探索未知环境,该方法旨在通过元学习的方式,提高智能体的探索能力。
在MAS中,Sunehag等人[16]提出了值分解网络(value decomposition networks,VDN)多智能体强化学习算法,将全局Q值分解为局部Q值的加权和,并在联合动作Q值中考虑各个智能体的行为特征,提高了多智能体系统的学习效果,但需要进一步平衡个体智能体的贡献和团队合作关系,以及如何处理高维状态空间等问题。Rashid等人[17]提出了QMIX算法,通过将值函数分解为单调函数和非单调函数的组合,以提高多智能体系统的学习效果,解决了值函数的高方差和不稳定性;然而该方法仍面临一些问题,如如何选择合适的值函数分解形式和如何处理大规模多智能体系统的挑战等。Foerster等人[18]提出反事实基线的多智能体策略梯度方法(counterfactual multi-agent policy gradients,COMA),通过引入对抗性训练和对抗性评估来进行策略优化,使用反事实基线对不同主体的贡献进行信用分配,从而提高多智能体系统的学习性能,解决了非平稳环境和非合作行为等问题,但在训练的稳定性和计算复杂度等方面有所欠缺。Lowe等人[19]提出MADDPG(multi-agent deep deterministic policy gradient)算法,使用集中式训练和去中心化执行机制,基于DDPG的每个智能体的全局Q值来更新本地策略,智能体能够在协作和竞争之间进行平衡以达到更好的性能,但在如何处理大规模多智能体系统和如何处理合作与竞争之间的平衡等方面存在不足。MAPPO(multi-agent PPO)[20]采用基于近端策略优化(proximal policy optimization,PPO)[21]的集中函数来考虑全局信息,智能体之间通过全局值函数实现相互协作,在处理合作多智能体环境时表现出良好的性能和鲁棒性,为解决合作问题提供了一种有效的方法。
元学习应用于MADRL中,从不同的角度解决了许多问题,如学习与谁沟通[22]、学习特定于智能体的奖励函数以实现机制设计的自动化[23],但是目前的研究仍然较少。Charakorn等人[24]提出了一种通过元强化学习与未知智能体合作的方法,该方法使智能体能够快速适应与未知智能体的合作任务,并取得良好的性能,但需要解决如何处理未知智能体的行为和如何在实际环境中应用该方法等问题。Feng等人[25]引入了神经自动课程(neural auto-curriculum,NAC),通过自适应调整游戏难度和规则,智能体能够通过自我学习来改进策略和适应对手,该方法在零和博弈中取得了良好的效果,但仍面临一些问题,即如何处理复杂博弈和如何扩展到更大规模的对抗环境等。为了解决多智能体环境下的非平稳问题,Foerster等人[26]提出了一种对手感知的学习方法(learning with opponent-lear-ning awareness,LOLA),通过考虑对手的策略和行为来指导智能体的学习过程,该方法能使智能体更好地适应对手的变化和策略调整,从而提高了在对抗环境中的学习性能。Kim等人[27]提出了一种多智能体强化学习中的元策略梯度算法,通过优化策略梯度来实现智能体的元学习,使得智能体能够通过学习适应性策略来快速适应多智能体环境,并取得更好的性能。Al-Shedivat等人[28]基于单智能体MAML设计了一种基于梯度的多智能体元学习方法,用于自适应动态变化和对抗场景,有效提高了多智能体强化学习的训练效率和适应速度。多智能体MAML在MAML算法架构中设计多智能体强化学习,且仅用两个智能体之间的交互过程。与多智能体MAML算法不同,MAMPPO方法是在不改变多智能体强化学习架构的前提下引入元学习;与多智能体MAML算法类似,MAMPPO将基于梯度的一阶元Reptile的思想用于多智能体环境中,以达到通过元学习提高多智能体强化学习算法性能的目的。
2 MAMPPO方法
本文提出的方法以MAPPO算法为基础,引入基于梯度的一阶元学习Reptile的思想,在学习过程中整合以往经验所需的元知识,并将其保存为模型参数初始化的规则,实现使用有限经验的持续学习和快速适应。
2.1 MAPPO算法
PPO是一种非常流行的RL算法,在各种单智能体任务场景中都有非常出色的表现。MAPPO是在MARL中应用的PPO的一种变体,采用集中训练分散执行框架(centealized training and decentralized execution, CTDE)。MAPPO框架如图1所示。
MAPPO算法的网络由AC网络支持,参数化的策略和值函数由两套独立的网络进行计算,不同智能体各自拥有一套策略网络并共享网络参数。中心控制器由一套值函数网络构成,全局值函数作为中心控制器,智能体将在全局状态s下将局部观察信息oi=O(s;i)传递给中心控制器,中心控制器根据全局状态信息进行训练,得到策略πθ,各智能体执行联合动作分布A=(a1,a2,…,an)。待训练完成后,智能体可以独立于中心控制器,仅根据自己的局部观察信息进行决策并执行最优动作。
为了使单智能体PPO算法适应多智能体的设置,局部观察信息设定为学习策略πθ和基于全局状态S的集中值函数V(s),并使用PopArt对V(s)进行归一化处理,策略函数πθ和价值函数V(s)分别由行动者网络(actor)和评论家网络(critic)产生。具体来说,critic网络将所有全局信息和一些特定于智能体的特征作为critic网络的输入,实现了从状态S到奖励R的映射;actor网络将智能体的观察信息映射到离散动作空间中的动作分布或者连续动作空间中的多元高斯分布的均值和标准差向量。另外在训练过程中,将无法执行的动作概率设为零,使用带有智能体特定标识的向量区分训练过程中死亡的智能体,并将其作为critic网络的输入。actor网络的训练目标是使损失函数L(θ)最大化,critic网络的训练目标则是使损失函数L()最小化。假设有n个智能体,B为小批处理数
2.2 MAMPPO方法设计
MAMPPO将基于一阶梯度的元学习思想应用到MARL设置中,提高MARL的泛化能力和训练速度,实现从有限经验中不断学习和适应的能力。其关键在于学习过程中整合以往经验所需的元知识,并将其保存为模型的初始参数,以实现有限经验的持续学习和快速适应。图2显示了MAMPPO框架。
MAMPPO首先按照MAPPO训练流程进行训练,存储交互过程中产生的数据元组并计算对应折扣累积奖励和奖励函数,将过程中产生的数据划分为不同的任务数据块(task data chunks)用于元更新。在元更新阶段,通过在任务数据块上反复采样进行元学习,经过一定次数的梯度下降进行参数软更新,完成对模型初始化参数的学习,实现在新任务上的快速微调。
最后更新后的网络模型参数满足梯度下降方向最敏感的要求,使模型在处理新任务时从最佳起点开始,有效提高了联合策略的决策效率。
算法1 MAMPPO方法
3 实验和结果讨论
在SMAC实验平台上进行实验,SMAC是研究CTDE算法的主流基准,具有连续的观察空间和离散的动作空间,有各种各样的地图,具有很高的学习复杂性。每个智能体都是独立的,组成一个小组与内置脚本AI竞争,适合在各种协作的多智能体情况下测试本文方法。在每场战斗中,每个智能体都需要给对方造成最大化伤害,并将自身承受的伤害最小化。
本文选择在一个简单地图(3 m)、两个困难地图(3s_vs_5z, 3s5z)和一个超难地图(corridor)上评估了本文方法。表1介绍了地图的特点,比较的方法有MAPPO、QMIX和VDN。其中,VDN算法将全局值函数分解为每个智能体的局部值函数的加权和,全局值函数考虑智能体个体行为的特性,使得该值函数更易于学习,能够解决多智能体系统中的合作与竞争问题,并且可在一定程度上缓解多智能体系统中环境不稳定的问题。QMIX采用混合网络模块将各智能体的局部值函数组合为全局值函数,通过对全局值函数进行因子分解,将智能体的局部值函数与一个可学习的混合函数相结合,使得每个智能体可以独立地選择行动,且同时考虑其他智能体的行动和全局信息,从而提高了整体协作效果。下面分别对MAMPPO的训练速度和适应性进行了评价。
在訓练实验中对模型进行多步训练,测量训练速度。除地图训练2M时间步外,其余地图训练5M时间步。在元学习过程中,适应的数量被设置为15,元更新中的步长设置为0.05。首先对训练过程中的胜率曲线图进行分析。
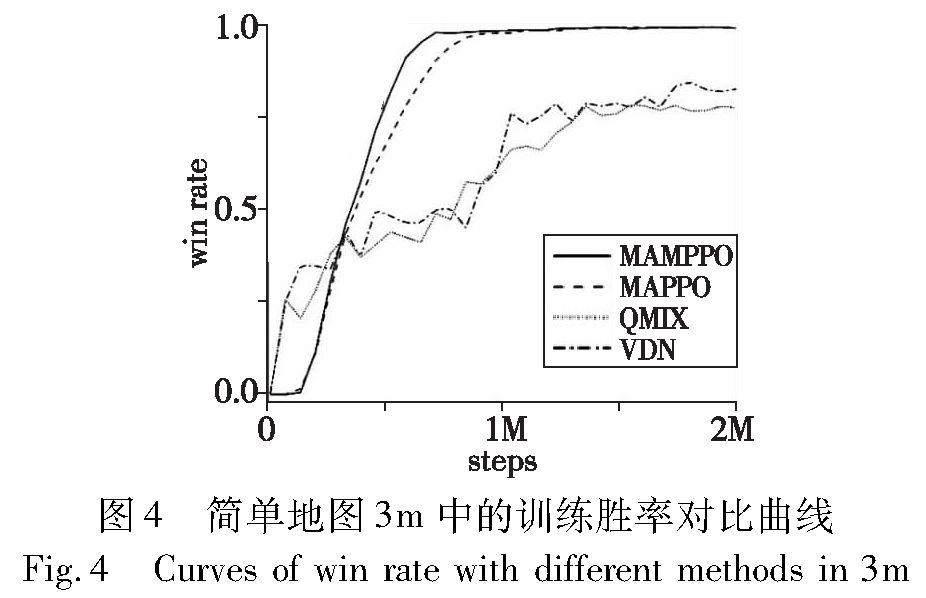
a)在简单地图3m中的胜率曲线对比如图4所示。可以看出,MAMPPO和MAPPO的胜率曲线远高于QMIX和VDN算法,虽然MAMPPO和MAPPO在1M时间步之后的曲线大体一致,但MAMPPO训练前期的胜率曲线斜率大于MAPPO且比其更早收敛,说明MAMPPO的训练效率有所提升。
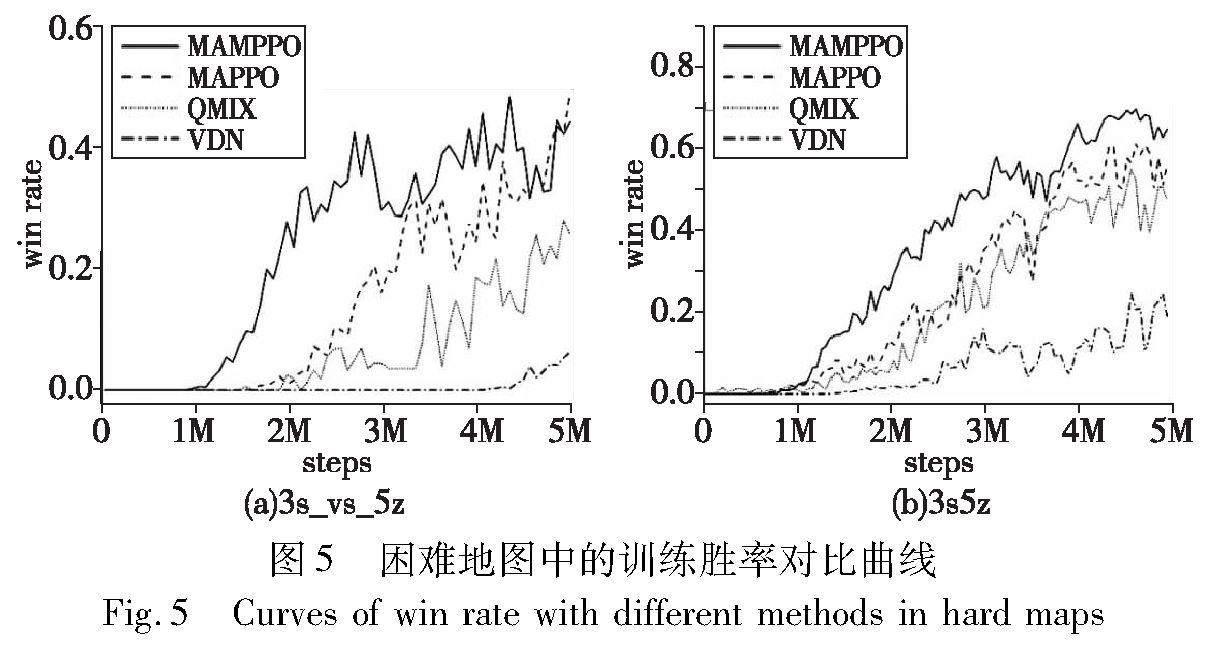
b)在困难地图(3s_vs_5z和3s5z)中的胜率曲线对比如图5所示。可以看出,MAMPPO训练前期的胜率曲线增长速率和训练结束所得的胜率明显高于其他三种算法,并且能够更快地收敛。在3s_vs_5z地图中,作战智能体为同构类型,共享一套网络参数,MAMPPO的胜率在1M时间步后率先大于0,说明由MAMPPO训练的我方作战智能体比其他算法训练的作战智能体出现获胜的场次更早。在3s5z地图中,作战智能体为异构类型,分别处理各自的网络参数,在整个训练过程中,MAMPPO的胜率曲线均高于其他三条曲线,说明经MAMPPO训练的作战智能体拥有更强的作战能力。
c)在超难地图corridor中的胜率曲线对比如图6所示。可以看出,MAMPPO的胜率曲线整体高于QMIX和VDN对应胜率,且略高于MAPPO的胜率曲线,因为超难地图中的敌方作战智能体较多,需要处理的数据也对应增加,增加了元更新阶段中反复适应的计算难度,训练过程中会出现计算量代偿的问题。
计算训练步最后10次的平均胜率,结果如表2所示。从表中可以看出,MAMPPO方法在简单地图3m中的平均胜率高于QMIX和VDN算法,并且与MAPPO算法的对应胜率持平。在困难地图(3s_vs_5z和3s5z)和超难地图corridor中的平均胜率均高于参与比较的三种算法,具体胜率提升百分比为:MAMPPO方法在3m、3s_vs_5z、3s5z、corridor地图中的胜率比MAPPO算法分别提高了0%、4.12%、16.93%、2.62%,比QMIX算法分别提高了28.55%、87.80%、39.58%、19.04%,比VDN算法分别提高了23.51%、514.66%、241.47%、342.48%。
因此在训练阶段,MAMPPO所学策略的改进速度明显加快,训练速度明显提高,训练所得的胜率高于其他方法,经过元学习训练的作战智能体的作战能力高于其他多智能体算法训练所得。
为了评估MAMPPO的适应能力,通过计算每次训练迭代32场后测试的胜率来测试MAPPO和MAMPPO训练的作战智能体的作战能力,并将最后10次测试所得胜率的中位数作为评估胜率,四种地图的评估胜率如表3所示。由表可得,除了在简单地图中的胜率恒为100%之外,经过MAMPPO训练的作战智能体在其他三个地图中取得的胜率均高于MAPPO训练所得,具体胜率提升百分比为:MAMPPO方法在3s_vs_5z、3s5z、corridor地图中的胜率比MAPPO算法在其上的胜率分别提高了37.02%、18.18%、11.73%。
因MAMPPO方法相较于MAPPO算法在困难地图(3s_vs_5z和3s5z)中的性能表现提升明显,在测试阶段选择这两个地图的测试胜率曲线对比如图7所示。
MAMPPO方法在困难地图(3s_vs_5z和3s5z)和超难地图corridor的评估胜率均高于MAPPO算法,表现出色。另外,虽然在简单地图3m中的评估胜率均为100%,但是MAMPPO方法在6K步时获得的作战智能体胜率便可以达到100%,MAPPO算法则需要在1M步时获得的作战智能体胜率达到100%。由困难地图(3s_vs_5z和3s5z)的评估胜率曲线可得,MAMPPO方法的胜率开始变化,时间步长早于MAPPO算法,说明MAMPPO方法训练所得作战智能体的适应能力强于MAPPO算法,更快地开始适应新的情况。相比于MAPPO算法,在相同时间步长的情况下,MAMPPO方法所得胜率高于MAPPO算法,说明模型适应性提升显著,作战智能体对训练场新情况的处理能力明显提升。MAMPPO方法在新任务情况下的评估胜率高于MAPPO算法,且适应速度显著提高,表明MAMPPO方法的自适应能力在引入元学习后有所提高。
实验结果表明,用MAMPPO方法训练得到的作战智能体在总体上取得了更优的性能,在训练场中能够更早更高效地探索出获胜策略,在相同训练时间步长情况下的训练速度明显提升,其训练所得的适应性明显增强,能够处理在训练场中出现的情况,表现了出良好的训练效率和适应能力。
4 结束语
本文将元学习引入到MADRL中,提出了一种MAMPPO方法,从元学习的角度提升多智能体算法性能,为解决多智能体泛化能力问题提供了一个新的视角。将基于梯度的元强化学习扩展到多智能体强化学习,在智能体完成交互后构建任务数据块,在模型参数更新阶段定义元梯度,并执行多次梯度下降来学习网络模型的初始参数。在SMAC环境下的实验结果表明,该方法在各种场景下的性能都优于基线方法,有效地提高了多智能体系统的强化学习性能,缩短了训练时间,进一步证实了将元学习引入多智能体强化学习的可行性。
然而在训练多个智能体的过程中,每个智能体的感知转移概率分布和奖励函数都会发生变化。从每个智能体的角度来看,环境具有非平稳性。如何从每个智能体的角度使用元学习,同时考虑自身的学习过程和环境中其他智能体的学习,是未来需要解决的问题。
参考文献:
[1]Silver D,Huang A,Maddison C J,et al. Mastering the game of Go with deep neural networks and tree search [J]. Nature,2016,529(7587): 484-489.
[2]Bellemare M G,Candido S,Castro P S,et al. Autonomous navigation of stratospheric balloons using reinforcement learning [J]. Nature,2020,588(7836): 77-82.
[3]Henderson P,Islam R,Bachman P,et al. Deep reinforcement learning that matters [C]// Proc of the 32nd AAAI Conference on Artificial Intelligence. Palo Alto,CA: AAAI Press,2018: 3207-3214.
[4]Miki T,Lee J,Hwangbo J,et al. Learning robust perceptive locomotion for quadrupedal robots in the wild [J/OL]. Science Robotics,2022,7(62). https://arxiv.org/abs/2201.08117.
[5]Yang Jiongzhi,Harish S,Li C,et al. Deep reinforcement learning for multi-phase microstructure design [J]. Computers,Materials & Continua,2021,68(1): 1285-1302.
[6]Berner C,Brockman G,Chan B,et al. Dota 2 with large scale deep reinforcement learning [EB/OL]. (2019-12-13). https://arxiv.org/pdf/1912.06680.pdf.
[7]Baker B,Kanitscheider I,Markov T,et al. Emergent tool use from multi-agent autocurricula [EB/OL]. (2020-02-11). https://arxiv.org/pdf/1909.07528.pdf.
[8]Nguyen T T,Nguyen N D,Nahavandi S. Deep reinforcement learning for multiagent systems: a review of challenges,solutions,and applications [J]. IEEE Trans on Cybernetics,2020,50(9): 3826-3839.
[9]Finn C,Abbeel P,Levine S. Model-agnostic meta-learning for fast adaptation of deep networks [C]// Proc of the 34th International Conference on Machine Learning. [S.l.]: PMLR,2017: 1126-1135.
[10]Xu Zhixiong,Chen Xiliang,Tang Wei,et al. Meta weight learning via model-agnostic meta-learning [J]. Neurocomputing,2021,432(4): 124-132.
[11]Nichol A,Achiam J,Schulman J. On first-order meta-learning algorithms [EB/OL]. (2018-10-22) [2023-09-19]. https://arxiv.org/pdf/1803.02999.pdf.
[12]Song Xingyou,Gao Wenbo,Yang Yuxiang,et al. ES-MAML: simple Hessian-free meta learning [EB/OL]. (2020-07-07)[2023-09-19]. https://arxiv.org/pdf/1910.01215.pdf.
[13]Wierstra D,Schaul T,Glasmachers T,et al. Natural evolution strategies [J]. Journal of Machine Learning Research,2014,15(1): 949-980.
[14]Stadie B C,Yang Ge,Houthooft R,et al. Some considerations on learning to explore via meta-reinforcement learning [EB/OL]. (2019-01-11)[2023-09-19].https://arxiv.org/pdf/1803.01118.pdf.
[15]Xu Tianbing,Liu Qiang,Zhao Liang,et al. Learning to explore with meta-policy gradient [C]// Proc of the 35th International Conference on Machine Learning. [S.l.]: PMLR,2018: 5463-5472.
[16]Sunehag P,Lever G,Gruslys A,et al. Value-decomposition networks for cooperative multiagent learning based on team reward [C]// Proc of the 17th International Conference on Autonomous Agents and Multi Agent Systems. 2018: 2085-2087.
[17]Rashid T,Samvelyan M,De Witt C S,et al. Monotonic value function factorisation for deep multi-agent reinforcement learning [J]. Journal of Machine Learning Research,2020,21(1): 7234-7284.
[18]Foerster J N,Farquhar G,Afouras T,et al. Counterfactual multi-agent policy gradients [C]// Proc of the 32nd AAAI Conference on Artificial Intelligence. Palo Alto,CA: AAAI Press,2018: 2974-2982.
[19]Lowe R,Wu Yi,Tamar A,et al. Multi-agent actor-critic for mixed cooperative-competitive environments [C]// Proc of the 31st International Conference on Neural Information Processing Systems. Red Hook,NY: Curran Associates Inc.,2017: 6379-6393.
[20]Yu Chao,Velu A,Vinitsky E,et al. The surprising effectiveness of PPO in cooperative multi-agent games [C]// Proc of the 35th Neural Information Processing Systems. Cambridge,MA: MIT Press,2022: 24611-24624.
[21]Schulman J,Wolski F,Dhariwal P,et al. Proximal policy optimization algorithms [EB/OL]. (2017-08-28)[2023-09-19]. https://arxiv.org/pdf/1707.06347.pdf.
[22]Zhang Qi,Chen Dingyang. A meta-gradient approach to learning cooperative multi-agent communication topology [C]// Proc of the 5th Workshop on Meta-Learning at NeurIPS. [S.l.]: Artificial Intelligence Institute,2021.
[23]Yang Jiachen,Ethan W,Trivedi R,et al. Adaptive incentive design with multi-agent meta-gradient reinforcement learning [C]// Proc of the 21st International Conference on Autonomous Agents and Multiagent Systems. 2022: 1436-1445.
[24]Charakorn R,Manoonpong P,Dilokthanakul N. Learning to cooperate with unseen agents through meta-reinforcement learning [C]// Proc of the 20th International Conference on Autonomous Agents and Multi Agent Systems. Richland,SC: IFAAMAS,2021: 1478-1479.
[25]Feng Xidong,Slumbers O,Wan Ziyu,et al. Neural auto-curricula in two-player zero-sum games [J]. Neural Information Processing Systems,2021,34(1): 3504-3517.
[26]Foerster J,Chen R Y,Al-Shedivat M,et al. Learning with opponent-learning awarenesss [C]// Proc of the 17th International Conference on Autonomous Agents and Multi Agent Systems. 2018: 122-130.
[27]Kim D K,Liu Miao,Riemer M D,et al. A policy gradient algorithm for learning to learn in multiagent reinforcement learning [C]// Proc of the 38th International Conference on Machine Learning. [S.l.]: PMLR,2021: 5541-5550.
[28]Al-Shedivat M,Bansal T,Burda Y,et al. Continuous adaptation via meta-learning in nonstationary and competitive environments [EB/OL]. (2018-02-23)[2023-09-20]. https://arxiv.org/pdf/1710.03641.pdf.

