分层土-隧道相互作用体系地震响应分析

张存 郑文 罗凯凯 路沙沙

摘要：为研究地震作用下非均质场地各个土层放大效应以及分层土-隧道的地震响应，以大连某实际工程为背景，基于地震作用下隧道结构动力响应的理论，采用收敛约束法，通过ABAQUS构建分层土-隧道三维有限元模型，并结合振动台试验，验证模拟的准确性;将自由场与有隧道场地进行对比，并结合加速度和傅里叶曲线对模拟数据进行分析。结果表明：（1）土体性质和激励大小对地震波的传递有影响，随着场地由浅到深逐渐增加，峰值加速度逐渐放大，不同分层介质的主要频率和频谱形状发生明显变化；（2）隧道会放大远场的加速度响应，略微降低近场的动力响应；（3）软弱夹层的存在对地震动的放大作用也有明显影响，不同分层介质的不同特性导致土层刚度不同，从而影响地震作用下层状土-隧道的动力相互作用。

关键词：放大效应; 分层土; 收敛约束法; 土-隧道结构相互作用; 数值模拟

中图分类号： U45      文献标志码：A   文章编号： 1000-0844（2024）03-0602-12

DOI：10.20000/j.1000-0844.20220804002

Seismic response of layered soil-tunnel interaction system

ZHANG Cun1， ZHENG Wen1， LUO Kaikai1， LU Shasha2

（1. China Construction Seventh Engineering Bureau， Zhengzhou 450000， Henan， China;2. College of Mechanics and Engineering， Liaoning Technical University， Fuxin 123000， Liaoning， China）

Abstract： This study used Dalian Metro as background to study the amplification effect of each soil layer in the heterogeneous site and the seismic response of a layered soil-tunnel system under seismic action. Based on the theory of dynamic response of tunnel structure under seismic action， a three-dimensional finite element model of the layered soil-tunnel was constructed with ABAQUS and a convergence constraint method. The simulation accuracy was verified by a shaking table test. Then， the free field was contrasted with the tunnel site， and the simulation data were analyzed in combination with the acceleration and Fourier curves. Results show that （1） the soil properties and excitation magnitude affect the transmission of seismic waves. As the site gradually increases from shallow to deep， the peak acceleration gradually increases， and the main frequencies and spectrum shapes of different layered media change obviously. （2） The tunnel amplifies the acceleration response in the far field and slightly reduces the dynamic response in the near field. （3） The weak interlayer has an evident influence on the amplification effect of earthquakes. The characteristics of different layered media lead to different soil stiffness， further influencing the dynamic interactions of the layered soil-tunnel during earthquakes.

Keywords：amplification effect; layered soil; convergence constraint method; soil-tunnel structure interaction; numerical simulation

0 引言

隨着我国对地下空间的不断开发，地铁隧道的安全成为不可忽略的问题，因此大量学者对地下结构抗震进行了研究。庄海洋等［1］利用ABAQUS软件研究了南京地下结构的水平向非线性的地震响应规律，根据模拟认为在地震作用下两层双柱岛式地铁车站结构的中柱和中板是最不利位置。谷拴成等［2］利用ANSYS及其提供的APDI程序，通过参数化设计语言对某地铁车站进行了数值模拟，讨论了地基土-地下结构的动力相互作用规律。Hou等［3］通过ABAQUS进行数值模拟，考虑竖向和水平地震波的相互作用，将日本地铁车站的破坏情况与有限元数值模拟结果进行对比，讨论了数值模拟研究土-结构的动力特性的准确性。陈国兴等［4］利用有限元软件ABAQUS进行模拟分析，研究了土-隧道在塑性损伤本构下的地震响应。以上研究均以均质土-隧道的地震响应为主，为工程前期抗震设计提供参考。

大连位于华北地震带，处于郯庐构造的边缘［5］，而郯庐地震带是华北地震带中最易发生地震的区域之一，因此地下隧道抗震也成为大连市隧道建设中不能忽视的技术问题之一。特别是分层土-隧道在地震作用下的动力响应对于隧道安全方面有着重要意义。吴祚菊等［6］采用大型振动台试验研究分层土中地震动的放大效应，研究表明在地震作用下场地中不同厚度的软弱夹层对地震动的放大效应影响显著。于辉等［7］通过ABAQUS数值模拟研究隧道在不同分层介质内的地震响应，研究表明土层的性质对土-隧道相互作用体系是有影响的。陈跃庆等［8］研究了不同分层介质对地震波传递的影响，结果表明土层特性对地震动的影响明显。

Chen等［9］利用有限元软件建立地下结构-土-地表结构的二维模型，并讨论其地震响应规律。胡小容等［10］以南昌地铁区间隧道为背景，将动三轴试验结果与PFC3D模拟结果进行对比，研究饱和含泥砂土的工况下隧道的动力特性。Idriss等［11］、Kennett［12］对地震波在水平场地和不同分层介质场地中的传递特性进行了探讨。

在实际工程中，由于地质演化和其他因素的影响，土体往往是非均质分布的。非均质地基的应力状态和变形特征往往与均质地基有很大不同，采用不同介质中的隧道模型更能够反映实际工程土体的特征。本文采用ABAQUS有限元分析软件，以大连地铁5号线04标段火车站—梭鱼湾南站为背景，基于地震作用下隧道结构动力响应的理论，结合收敛约束法建立了分层土-隧道模型，研究地震作用下不同分层介质的频谱变化以及不同场地分层土-隧道的地震响应规律。

1 工程概况

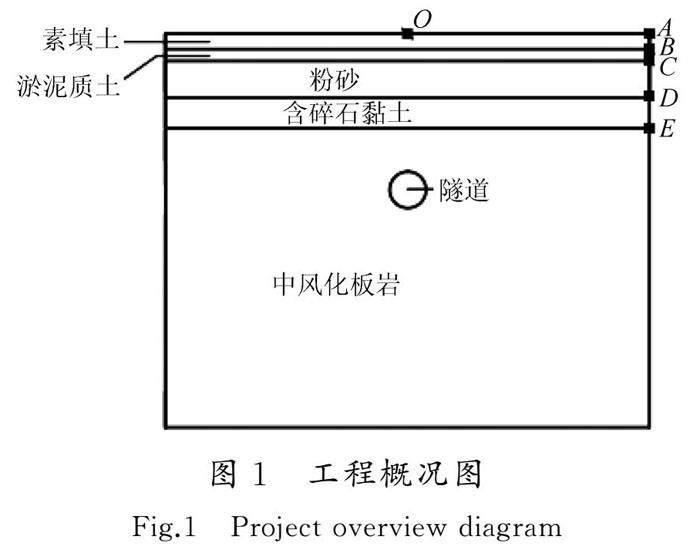
本文以大连地铁5号线04标段火车站—梭鱼湾南站区间隧道为研究对象。整个隧道断面位于中风化板岩层，假设地表和各岩土层为水平层状。场地地层从上往下依次为素填土、淤泥质土、粉砂、含碎石黏土、中风化板岩。根据勘察资料，各地层分述如下：（1）素填土：层厚为5.8 m;（2） 淤泥质土：层厚为1.7 m;（3）粉砂：层厚为3.2 m;（4）含碎石黏土：层厚为2.5 m;（5）中风化板岩：层厚为51.2 m（图1），隧道顶部与地表净距17.2 m。区间隧道各岩土层物理力学参数如表1所列。

大连地铁5号线工程海域段地貌为海漫滩及海湾，陆域地段经过人工回填。大连地铁隧道结构设计参数为：隧道管片内径和外径分别为10.8 m和11.8 m，环宽2.0 m，管片厚度50 cm。大连地铁5号线04标段火车站—梭鱼湾南站区间隧道场地地形平坦，地层分布相对均匀稳定，但由于软弱土层的存在，该场地的抗震性能值得关注。

2 计算原理及方法

2.1 地震作用下隧道结构动力响应

当发生动力扰动（地震荷载、机械扰动或矿震）时，在静力与动力荷载联合作用下［13-14］，土-隧道結构复合结构体系的动力学方程为：

M+C+R（x）=F+F（t） （1）

式中：M为土-隧道结构的复合质量;

C为土-隧道组成的复合黏聚力;

F为土-隧道结构所承受的静力荷载外力的合力;

x为外力荷载作用下，土-隧道结构所产生的变形位移;F（t）为地震荷载;R（x）为土-隧道结构的抗力;

令K为土-隧道结构的弹性抗力系数，在外力扰动作用下，处于弹性变化阶段时，R（x）=Kx。

在动力荷载的扰动作用下土-隧道结构在水平方向（x方向）上会产生一定的位移。假设在动力荷载作用下土-隧道结构所产生的应力为σ，应变为ε，位移为x。 应力波在传播过程中的波动方程为：

2x′t2=c202x′X2 （2）

式中：c0为扰动荷载应力波的传播速度，单位为m/s;x′= x-x0为扰动荷载应力波引起的位移变化。

基于工程结构波动理论可知，应力波的传播速度为：

c0=λ+2μρ （3）

式中：λ、μ为拉梅常数。

对式（2）进行求解变换可以得到：

μ′（x，t）=f（x-c0t）+g（x+c0t） （4）

式中：

f（x-c0t）为应力波入射纵波的波动方程;g（x+c0t）为应力波反射纵波的波动方程。

联合式（1）～（4）得到：

ε=ε0+′μxx=ε0+f（x-c0t）x+g（x-c0t）x

σ=Eε=Eε0+Ef（x-c0t）x+g（x-c0t）x

x′=′μxx=-c0f（x-c0t）x+c0g（x-c0t）x（5）

基于式（5），可以求得在应力波的作用下隧道结构内部的应力σ、应变ε、位移响应x的数值解，从而可以较好地判断隧道结构的地震动力破坏机理。

2.2 场地土层位移响应

采用假定地层变位法，确定刚度较均匀的成层分布地层的地震反应水平位移随深度的变化和土层相对位移。地震作用下土层沿深度方向位移公式为：

u（z）=12umax·cosπz2H （6）

式中：

u（z）为深度z处自由土层的地震反应位移，单位为m;umax为场地地表最大水平位移，单位为m;z为地下结构面距地表的深度，单位为m;H为地震基准面距地表面的深度，单位为m。

取土体与结构间的相对变形值为地震作用下结构周边土层发生的最大水平位移，则土层相对位移计算公式为：

u′（z）=u（z）-u（zB） （7）

式中：

u′（z）为深度z处相对于结构底部的自由土层相对位移，单位为m;

u（zB）为深度zB处自由土层地震反应位移，单位为m。

3 建立数值模型

3.1 基于弹塑性分析的收敛约束法

弹塑性分析又称弹性极限平衡分析。Fenner和H.Kastner假设破坏后岩体体积不变，以摩尔-库仑准则为基础［15］，采用理想弹塑性模型，得到了地下洞室围岩特征曲线。这一结果使人们认识到，如果支护阻力较小则可以充分发挥围岩的自承载能力，从而获得围岩的稳定性。因此，Fenner和H.Kastner的研究成果［15］被新奥方法和收敛约束方法广泛推广和采用，成为他们理论基础的重要组成部分。随着隧道施工监控水平的不断提高，收敛约束法［16］的理论逐渐应用于实际隧道工程中，主要体现在隧道的设计和稳定性分析中。根据施工过程中隧道断面的实测变形，将隧道开挖视为围岩应力重新分布的过程［17-20］。因此，建立科学、合理的隧道模型，对模拟围岩应力释放的仿真具有十分重要的意义。

本文将收敛约束法应用于模型结构侧面的结点，得到了与地震作用下自由场模拟分析相平衡的结点作用力。在此基础上，对各结点施加结点作用力，使结点力随着时间的推移而减小。当其降低到一定程度时，衬里单元被激活，然后剩余载荷衰减。利用ABAQUS软件，以围岩应力释放为重点，建立收敛约束的分层土-隧道模型，然后系统地讨论了分层土-隧道的地震响应规律。

3.2 模型荷载和接触

本文数值模拟以大连地铁5号线04标段火车站—梭鱼湾南站区间隧道为研究对象，在选择地震波时采用大连地区地震时的类似地震波El-Centro波。本文共设置了两种场地类型，分别为自由场地与有隧道场地，依次输入0.1g～0.6g El-Centro波，Kobe波以及超越概率为10%的人工地震波来模拟大连地震作用，模拟输入压缩后地震波的持续时间为10 s左右。图2为0.1g El-Centro波、0.1g Kobe波以及0.1g人工波的加速度时程曲线。

模拟前需做以下假设：（1）考虑土体的自重应力场;（2）考虑分层土-隧道之间的动力相互作用;（3）未考虑地下水渗流对隧道结构的影响。

根据已有的研究［21］，在均匀、弹性半无穷大区域内建立圆形隧道模型，其应力和位移的变化在3倍直径范围内的5%左右，而在5倍以上的范围内则不到1%。为克服边界条件的影响，模型的横向宽度设为隧道直径的3～5倍。故几何模型横向长度177 m，纵向长度30 m，竖向高度64.4 m，隧道位于模型土体中部，顶部与地表净距17.2 m，左右两侧与边界净距82.6 m。根据大连地铁的场地条件，采用摩尔-库仑本构模型和收敛约束法建立分层土仿真模型。为了考虑分层土-隧道的动力相互作用，在隧道-土接触部分设置接触对，接触面的法向行为是“硬”接触，切向行为表现为库仑摩擦的罚函数形式，相关参数如表1所列［22］。支护结构初衬材料为C60，厚度为30 cm，模型初衬的参数如表2所列。

分层土-隧道模型的单元类型采用三维八结点线性减缩积分实体（C3D8R），采用扫掠技术并按照从边界到隧道逐渐加密的原则进行网格划分。假设隧道施工前初始地应力仅与土体的自重有关。上表面为自然地面，选择土体的自重方向为Y方向。在建模过程中，水平和竖向位移约束被应用于模型的左、右、前和后。模型底部直接固定，表面为自由边。分层土-隧道结构的有限元几何模型如图3所示，图中①～⑤分别代表的土层为：素填土、淤泥质土、粉砂、含碎石黏土、中风化板岩。

4 数值模拟结果与分析

4.1 数值结果与振动台试验数据对比分析

利用工作频率为0～50 Hz刚性振动台模型箱研究地震作用下复杂场地的动力响应。振动台试验土体尺寸为1.6 m（长）×1.6 m（宽）×1.3 m（高）。试验按照采用量纲分析、相似理论和控制方程法进行相似比设计，为了考虑系统弹性地震反应规律，选择有机玻璃来模拟隧道结构的弹塑性地震反应。有机玻璃的密度为1 180 kg/m3，弹性模量为3 GPa，相应的密度相似比为0.442，盾构隧道弹性模量相似比0.088。非均质场地由上至下共分为5 层，第5层为人工模拟的基岩。本试验对应的模型隧道轴线埋深0.57 m，外径0.29 m，长度0.7 m，模型箱如图4所示。利用加速度传感器获取到自由场不同深度、不同层位监测点的加速度峰值、时程、反应谱等量测结果。为有效降低侧边界对加速度记录的影响，采用5个微型加速度计均布设在模型箱每层土的中部，且从下至上均匀布设。自由场下各层加速度时程曲线如表3所列，该试验实测加速度响应与本文数值模拟计算结果较为吻合，表明了数值模拟结果具有较好的准确性及可靠性。

4.2 土层频谱分析

本小结通过在自由场输入0.1g El-Centro波来研究不同岩土层的频谱变化。自然地震记录的地震波基本频率是0～10 Hz，共有3个标准分段，分别为0～1 Hz、1～5 Hz、5～10 Hz。El-Centro波的主要频率在0～15 Hz之间，因此，地震波的低频、中频、高频部分被划分为0～1、1～5和5～15 Hz共3个标准分段。

从图5（a）～（e）可以看出，地震波在基巖中传播的频率成分较丰富，随着场地深度由浅到深的变化，不同性质的土层的频率成分也在发生变化：

（1） 当El-Centro波从基岩向中风化板岩传播时，频谱中心频率峰值由1.3 Hz增加到2.25 Hz，所有频率分量（包括主频部分和次主频部分）向低频率方向移动约2 Hz。（2）当El-Centro波从中风化板岩传播到含碎石黏土层时，高频部分和中心频段的频率显著增加。（3）从含碎石黏土层到粉砂层，经中风化板岩过滤弱化的高频成分显著增加，与基岩和含碎石黏土相比，高频成分也明显增加。（4）从粉砂到淤泥质土土层，可以看出高频率部分中的成分明显变少，即软土中地震波的频谱主要是以低频为主，而地震作用下，地震频谱高频部分（5～15 Hz）的吸收非常显著。（5）从淤泥质土到素填土，被软土（淤泥质土）过滤的高频部分重新增强。总之，随着多相介质的界面折射、反射和散射地震波，地震波作用域多相介质中的传播频谱发生变化。

综上所述，地震波的频率分布在基岩中最丰富，且粉砂层对地震波的放大效应最为明显。自由场地和含隧道场地中对地震波的高频部分（5～15 Hz）的吸收非常显著。根据图5可以看出：随着场地由浅到深逐渐变化，主要频率不断增加且幅值增加明显，其幅度大小从2.25 Hz增加到3.25 Hz左右。主频左侧0～2 Hz频率分量增加显著，主频的局部频谱图从粗短型逐渐变得尖细型。

4.3 加速度响应对比分析

本节计算分析均是基于分层土模型，幅值为0.1g、0.3g、0.6g的El-Centro波输入。模型的原点定于土体表面的中点（图1中O点）的地表水平加速度幅值以及加速度曲线随着输入地震波的增大而不断变化，体现了地下隧道对分层土场地的地震响应影响。因此，对分层土-隧道在不同工况下以及不同激励大小下进行了系统分析。

图6为自由场地和有隧道场地在El-Centro波作用下加速度时程曲线和频谱曲线的对比。通过对比可以得出：在自由场场地下，随着输入地震波幅值的增大，低频率（0～2 Hz）明显增大，高频率（4～7 Hz）明显减小，中频率（2～3 Hz）趋于增大。在有隧道场地下，随着地震波幅值的增加，地震波的高频部分变化并不明显；对于低频部分，随着地震波幅值的增大，放大效应与自由场相比较弱；随着激励大小的增加，中频部分呈现单调放大的趋势，并且表现出比高频部分更显著的放大效果。综上所述，随着场地输入激励大小的增加，自由场对地震波频率的放大效应明显高于隧道场地，隧道起到明显的隔震作用。

在0.3g和0.6g的El-Centro波作用下，隧道场地下的地表加速度仍有轻微的放大效应，可能是由于地震波的散射和干扰导致能量在隧道正上方汇聚，从而放大了此时的峰值加速度。从频谱图可以看出，地震波传播的高频被土层过滤，而低频则更为明显。可以认为，基岩输入地震波的峰值加速度越大，对应监测点的峰值加速度绝对值越大（与低峰值输入结果相比）。输入地震波的幅值大小对地震波的传递有明显影响。随着地震波幅值的增加，地表加速度峰值呈现出小震作用下普遍放大，但大震作用下递减的趋势。

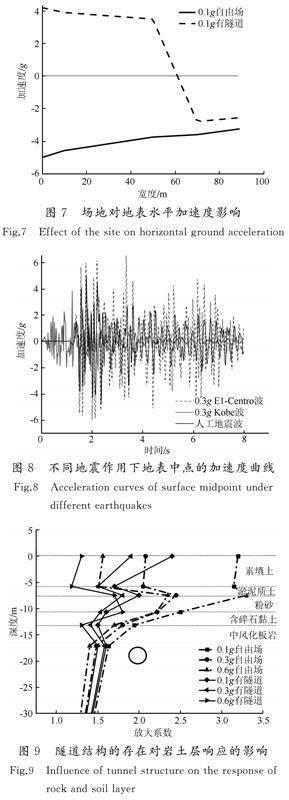
由于隧道位于中间位置，所以取模型中点的一半研究地表加速度变化情况（图7）。结合图6可以看出地表加速度的变化规律：地表加速度在O点时加速度最大，从中点向两边地表加速度呈减小趋势。在0.1g的El-Centro波作用下，有隧道场地中地表中点的地表加速度有显著减小，在强震下地表加速度的影响则更为明显。

地表中点加速度在0.3g El-Centro波、0.3g Kobe波以及0.3g人工地震波的加速度时程曲线如图8所示。通过三种不同地震波作用下的结果对比，发现 El-Centro波作用下峰值加速度最大，约 6.2 m/s2；超越概率10%的人工合成地震波次之，约5.04 m/s2;而Kobe地震波作用下峰值加速度最小，约3.8 m/s2 。相同峰值的加速度输入时，不同波形地震波激励下的反应存在差别，且El-Centro波或者越概率10% 的人工合成地震波比Kobe波激励下的反应略大。

4.4 加速度放大系数对比

如图9所示，依次测得A、B、C、D、E点（图1）的峰值加速度放大系数，主要研究隧道存在对土层加速度响应的影响。可以得出：在自由场场地，传输到地表的加速度随输入地震波强度的增加而增大;在有隧道工况，由于隧道的存在，地表放大系数相比自由场地的峰值加速度放大系数有所减小，但埋深17.2 m隧道处的放大系数却略大于自由场相应位置处的峰值加速度放大系数，且入射地震波峰值加速度越小，差值就越明显。造成这种现象的原因可能是地震波难以通过空心隧道结构，一些能量在隧道周围积聚和耗散，导致地震波到达地表时地震强度降低。在分层土-隧道体系中，不同土层传递振动的效果有所差异，同时输入地震波幅值的大小对地震波的传递也有着显著影响。

在素填土中，放大系数随着输入的El-Centro波幅值的增大而逐渐减小，但是整体该土层呈放大趋势。对于淤泥质土土层，在输入地震波幅值较小时起到放大作用，由于地震作用时孔隙水压力的增大，该层土体很快变软并发展成非线性，从而起到减振、

隔振的作用；在中震和大震中，该层的加速度放大系数随之降低。在粉砂层中，当输入地震波幅值小于0.3g时，峰值加速度放大系数随场地深度增大而增大;当输入地震波幅值大于0.3g时，土层的加速度放大效应随着砂土骨架的堆积损坏，动孔隙水压力上升，黏土骨架变软，及有效应力减小而不断衰减，同时沿着地震向上方传递振动降低。含碎石黏土和中风化板岩石土层对地震波基本上不起放大作用。

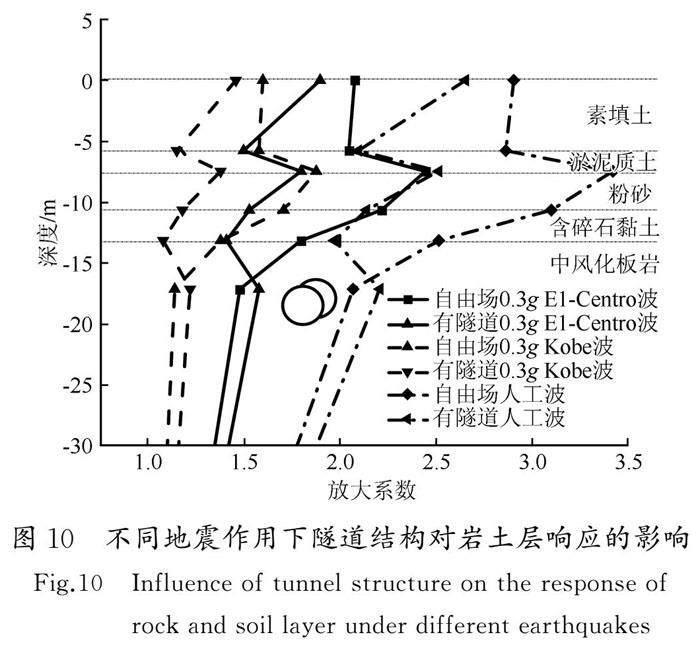
如图10所示为不同地震作用下隧道结构对土层响应的影响。可以看出，在同一强度的地震作用下，0.3g人工地震波下和0.3g El-Centro波下各土层的放大系数比0.3g Kobe波对于岩土层的影响更大。说明有隧道情况下的场地土层放大系数略低于自由场地下的場地土层放大系数。

4.5 土层位移响应

从土体位移幅值分布图11中可以得出如下规律：（1）地震作用下自由场下的土层位移比有隧道场地下的土层位移略大，且各土层位移随着地震波强度的增加而增大;（2）在0.1g El-Centro波输入时，土体未进入强非线性反应阶段，从中风化板岩层往上位移反应逐步增大，位移最大处为上覆淤泥质土层，土体侧向达到7 mm以上;（3）0.2g～0.6g El-Centro波输入时，粉砂与含碎石黏土层最土体位移反应较小，淤泥质土层最土体位移幅值最大，最大位移接近50 mm，由于中风化板岩层刚度较大，在0.6g El-Centro波作用下，土体侧向变形也较小，只有40 mm左右;（4）同一强度不同地震波作用下，0.3g El-Centro波与0.3g人工地震波下的土层位移较0.3 Kobe波下土层位移略大。

5 隧道地震响应分析

5.1 应力响应分析

为了便于计算结果分析，在隧道衬砌模型设置20个监测点如图12所示。图13给出了0.1g～0.6g的El-Centro波地震动作用下，隧道在不同强度地震波作用下的不同相位隧道中心截段的最大应力分布极坐标图。注意到由于不同工况下应力最大值变化的差值相较于隧道直径很小，因此图中缩小了原点附近的比例以更清晰地进行对比分析。分析可得：

（1） 隧道中心截段的最大应力分布呈对称分布，隧道中心截面上、下最大应力呈“凹”状，即隧道应变的形状为椭圆形。

（2） 隧道中心截面左右两侧应力较小，隧道在地震荷载作用下的最大应变发在与水平线呈斜45°处。因此，建议在盾构隧道管片安装时管片接缝应避开最不利位置，同时对穿越该位置的管片应加强其抗拉和抗剪强度。

（3） 在不同强度El-Centro波的输入下，分层土-隧道在不同相位下的隧道中心截段的最大应力分布情况大致相似，只是具体应变值有所差异;且隧道具有很大的拉应力响应。可以判断，在既有初始应力条件下，大连地铁顶部受拉，但在衬砌和锚杆的作用下，地铁底部可以保持稳定。

（4） 在相同强度不同地震波作用下，El-Centro波与0.3g人工地震波下的隧道应力大于Kobe波下隧道应力。

5.2 峰值加速度响应分析

隧道的拱顶和拱底在各种强烈地震波影响下的峰值加速度的变化，如图14所示。

可直观地发现：（1）在不同峰值加速度下，隧道结构的最大竖向加速度极值呈线性分布。（2）隧道会加大远场的加速度响应，而略微减小了近场的动力响应;随着输入的峰值加速度的提高，隧道结构的加速度对时程响应亦随着提高。（3）在0.1g峰值加速度下，隧道拱顶与拱底之间的加速度极值差别不大，但随着峰值加速度上升时拱顶的竖向加速度时程响应显著超过了拱底，并且差距逐渐增大。综上，对隧道结构的拱顶抗震设计需要多加注意。

如图15所示为地震动作用下不同深度土层峰值加速度的放大系数。可以得出：（1）随着在不同强度的El-Centro波的输入下，峰值加速度放大系数在逐渐降低，但是整体呈放大趋势;（2）软土层淤泥质土的存在对于地震响应在0.4g～0.6g地震动作用下有明显的减小作用，在0.1g～0.3g地震动作用下该土层有轻微放大效果;（3）不同土层对于地震动的放大效果是有差异的。相同强度地震波作用下El-Centro波与0.3g人工地震波下的土层峰值加速度的放大系数大于Kobe波下土层峰值加速度的放大系数。

5.3 内力分析

测取沿着隧道纵向长度L的剪力变化曲线，如图16所示。这6组曲线分别是0.1g～0.6g El-Centro波作用下隧道剪力变化，这6组曲线不但剪力变化趋势大概一致，而且沿着隧道呈对称分布。显然不同部位的轴力变化是存在差异的。当L<15 m时，随着L增大，剪力先增后减;当L>30 m后，随着L继续增大，6组曲线均结束明显变化，剪力先增加后减小。但是在0.2g和0.3g El-Centro波作用下隧道剪力的值与其余4组相反，可见受附加应力场影响，在一定范围内隧道剪力的变化趋势并不同步，这会使得隧道某一区域出现应力集中。由图17可知，随着激励大小的增加隧道结构的动弯矩峰值也会增大。PGA=0.3g时隧道结构动弯矩发生转折，之后随着输入波峰值的增加，结构动弯矩增长逐渐缓慢。相同强度地震波作用下El-Centro波与人工波下隧道剪力值大于Kobe波下隧道剪力值。

5.4 水平位移分析

依次输入0.1g～0.6g El-Centro波后得到的隧道结构最大相对水平位移如图18所示。可以看出：隧道结构的横向位移随着输入峰值加速度的增大而增大;隧道顶板以下8 m左右的最大相对水平位移大于其他位置，为最不利位置。当基岩输入不同强度的El-Centro波时，隧道结构的最大相对水平位移具有相同的趋势。相同强度地震波作用下El-Centro波与0.3g人工地震波下隧道结构相对水平位移大于Kobe隧道结构相对水平位移。在强震作用下，隧道的相对位移相对稳定，因此在现有条件下，大连地铁的衬砌和锚杆能够保持地铁的稳定性。建议构建时避开最不利位置，采取提高抗拉和抗剪強度的构造措施。

6 结论

本文基于ABAQUS大型有限元计算平台，对大连地铁5号线04标段火车站—梭鱼湾南站区间，在里程K9+604～707处隧道进行了三维数值模拟，得到地震波在自由场地与有隧道场地中各土层的特点以及隧道的地震响应规律。主要规律如下：

（1） 地震作用下，粉砂层对地震动的放大效应最强;中风化板岩层的频谱成分最丰富;淤泥质土层明显削弱地震动，降低地震动的高频分量。即软弱夹层可以明显地吸收地震波的高频分量;传播至素填土时，高频分量再次加强。这是由于多相介质的界面发生折射、反射和散射，导致地震波作用多相介质中的传播频谱发生变化。

（2） 自由场地对地震波频率的放大效应明显高于隧道场地，隧道起到明显的隔震作用。隧道场地下各土层的加速度响应的规律：对于粉砂层和淤泥质土，小震时有放大作用；对于含碎石黏土和中风化板岩石层，地震波的传递基本上呈放大趋势。

（3） 基于地震作用下隧道结构动力响应的理论，隧道应变主要发生在与水平方向成45°斜交的方向;地震作用下隧道内力先增大后减小;隧道顶板以下8 m左右的最大相对水平位移大于其他位置，为最不利位置，应采取提高抗拉和抗剪强度的构造措施。

参考文献（References）

［1］ 庄海洋，陈国兴，胡晓明.两层双柱岛式地铁车站结构水平向非线性地震反应分析［J］.岩石力学与工程学报，2006，25（增刊1）：3074-3079.

ZHUANG Haiyang，CHEN Guoxing，HU Xiaoming.Analysis of nonlinear earthquake response of two-layer double-column subway station structure［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（Suppl01）：3074-3079.

［2］ 谷拴成，朱彬，杨鹏.地下结构地震反应非线性分析［J］.地下空间与工程学报，2006，2（5）：748-752.

GU Shuancheng，ZHU Bin，YANG Peng.Nonlinear analysis of seismic responseof underground structure［J］.Chinese Journal of Underground Space and Engineering，2006，2（5）：748-752.

［3］ HUO H B，ANTONIO B.Seismic design of cut and cover rectangul ar tunnels-evaluati on of observed behavi or of Dakai station during Kobe earthquake，1995［C］//Proceedings of the 1st World Forum of Chinese Scholars in Geotechnical Engineering.Shanghai：Tongji University，2003：456-466.

［4］ 陈国兴，左熹，庄海洋，等.地铁车站结构大型振动台试验与数值模拟的比较研究［J］.地震工程与工程振动，2008，28（1）：157-164.

CHEN Guoxing，ZUO Xi，ZHUANG Haiyang，et al.A comparison between large-size shaking table test results and numerical simulation of a subway station structure［J］.Journal of Earthquake Engineering and Engineering Vibration，2008，28（1）：157-164.

［5］ 时忠超.地震灾害预测地理信息管理系统的设计与实现［D］.大连：大连海事大学，2023.

SHI Zhongchao.Design and implementation of geographic information management system for earthquake disaster prediction［D］.Dalian：Dalian Maritime University，2023.

［6］ 吴祚菊，张建经，王志佳，等.地震动场地放大效应的时频特性分析［J］.岩土力学，2017，38（3）：685-695.

WU Zuoju，ZHANG Jianjing，WANG Zhijia，et al.Time-frequency analysis on amplification of seismic ground motion［J］.Rock and Soil Mechanics，2017，38（3）：685-695.

［7］ 于辉，赵国臣，徐龙军，等.穿越上软下硬地层海底隧道衬砌横向地震响应分析［J］.地震工程与工程振动，2021，41（2）：211-218.

YU Hui，ZHAO Guochen，XU Longjun，et al.Analysis of submarine tunnel linings in rising region crossing upper soft and lower hard stratum to transversal seismic load［J］.Earthquake Engineering and Engineering Dynamics，2021，41（2）：211-218.

［8］ 陈跃庆，吕西林，侯建国，等.不同土性地基中地震波传递的振动台模型试验研究［J］.武汉大学学报（工学版），2005，38（2）：49-53.

CHEN Yueqing，L Xilin，HOU Jianguo，et al.Shaking table model testing on transfer of earthquake wave in various ground soils［J］.Engineering Journal of Wuhan University，2005，38（2）：49-53.

［9］ CHEN J Y，HE W，XU Q，et al.Impact analysis of underground structure on seismic response of site and surface buildings［J］.Journal of Dalian University of technology，2012，52 （3）：393-398.

［10］ 胡小榮，蔡晓锋，李春博，等.南昌地铁饱和含泥砂土动力特性模拟分析［J］.地下空间与工程学报，2021，17（增刊1）：157-173，195.

HU Xiaorong，CAI Xiaofeng，LI Chunbo，et al.Numerical simulations of dynamic characteristics for saturated compacted clayey sands in Nanchang metro［J］.Chinese Journal of Underground Space and Engineering，2021，17（Suppl01）：157-173，195.

［11］ IDRISS I M，SEED H B.Seismic response of horizontal soillayers［J］.Journal of the Soil Mechanics and Foundations Division，1968，94（4）：1003-1031.

［12］ KENNETT B L N.Seismic wave propagation in stratifiedmedia［M］.Cambridge：Cambridge University Press，1983.

［13］ 何滿潮，钱七虎.深部岩体力学基础［M］.北京：科学出版社，2010.

HE Manchao，QIAN Qihu.The basis of deep rock mechanics［M］.Beijing：Science Press，2010.

［14］ 魏晓刚，麻凤海，刘书贤.煤矿采空区岩体结构及地面建筑地震安全防护［M］.北京：科学出版社，2016.

WEI Xiaogang，MA Fenghai，LIU Shuxian.Seismic safety protection of rock mass structure and ground buildings in coal mining areas［M］.Beijing：Science Press，2016.

［15］ 刘高.高地应力区结构性流变围岩稳定性研究［D］.成都：成都理工大学，2002.

LIU Gao.Study on stability of structural rheological surrounding rock in high geostress area［D］.Chengdu：Chengdu University of Technology，2002.

［16］ 唐雄俊.隧道收敛约束法的理论研究与应用［D］.武汉：华中科技大学，2009.

TANG Xiongjun.Theoretical research and application of tunnel convergence constraint method［D］.Wuhan：Huazhong University of Science and Technology，2009.

［17］ 杨友彬，郑俊杰，赖汉江，等.一种改进的隧道开挖应力释放率确定方法［J］.岩石力学与工程学报，2015，34（11）：2251-2257.

YANG Youbin，ZHENG Junjie，LAI Hanjiang，et al.A revised method for calculating stress release ratio in tunnel excavation［J］.Chinese Journal of Rock Mechanics and Engineering，2015，34（11）：2251-2257.

［18］ 赵勇，李术才，赵岩，等.超大断面隧道开挖围岩荷载释放过程的模型试验研究［J］.岩石力学与工程学报，2012，31（增刊2）：3821-3830.

ZHAO Yong，LI Shucai，ZHAO Yan，et al.Modeltest study of surrounding rock load releasing during super-large section tunnel excavation［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31（Suppl02）：3821-3830.

［19］ 张常光，曾开华.等值地应力下岩质圆形隧道位移释放系数比较及应用[J].岩石力学与工程学报，2015，34（3）：498-510.

ZHANG Changguang，ZENG Kaihua.Comparison and application of displacement release coefficients for rock circular tunnels under equivalent ground stress[J].Journal of Rock Mechanics and Engineering，2015，34（3）：498-510.

［20］ 夏永旭，王文正，胡庆安.围岩应力释放率对双联拱隧道施工影响研究［J］.现代隧道技术，2005，42（3）：1-4.

XIA Yongxu，WANG Wenzheng，HU Qing'an.A study on the effect of the rate of stress relieving of surrounding-rocks on the construction of a double arch tunnel［J］.Modern Tunnelling Technology，2005，42（3）：1-4.

［21］ 左熹，陈国兴，王志华，等.软弱场地上地铁车站结构近远场地震反应特性振动台试验［J］.土木工程学报，2010，43（增刊2）：299-305.

ZUO Xi，CHEN Guoxing，WANG Zhihua，et al.Shaking table test on the seismic response of subway station structure in soft sites under near and far field ground motion［J］.China Civil Engineering Journal，2010，43（Suppl02）：299-305.

［22］ 李雨润，闫志晓，张健，等.饱和砂土中直群桩动力响应离心机振动台试验与简化数值模型研究［J］.岩石力学与工程学报，2020，39（6）：1252-1264.

LI Yurun，YAN Zhixiao，ZHANG Jian，et al.Centrifugal shaking table test and numerical simulation of dynamic responses of straight pile group in saturated sand［J］.Chinese Journal of Rock Mechanics and Engineering，2020，39（6）：1252-1264.

（本文编辑：任 栋）

基金项目：辽宁省教育厅项目（LJKZ0336）

第一作者简介：张 存（1997-），女，硕士，从事工程地质与岩土工程方面的研究。E-mail：1364014736@qq.com。

通信作者：罗凯凯（1995-），男，工程师，从事岩土工程方面的研究。E-mail：770946804@qq.com。

张存，郑文，罗凯凯，等.分层土-隧道相互作用体系地震响应分析［J］.地震工程学报，2024，46（3）：602-613.DOI：10.20000/j.1000-0844.20220804002

ZHANG Cun，ZHENG Wen，LUO Kaikai，et al.Seismic response of layered soil-tunnel interaction system［J］.China Earthquake Engineering Journal，2024，46（3）：602-613.DOI：10.20000/j.1000-0844.20220804002