基于等损伤的主余震序列型地震动PGA放大系数谱研究
雍飞 公茂盛 杨游

摘要:大地震發生后往往会伴随强余震发生,强烈余震会加重结构的破坏程度,在抗震设计及结构损伤评估中考虑余震的影响是一重要课题。采用NGA-West2数据库建立主余震序列型地震动记录数据集,基于损伤等效思想定义主余震作用下PGA放大系数α,针对单自由度体系结构,通过动力时程分析建立不同相对强度、不同场地条件下平均PGA放大系数谱,进一步通过回归分析构建PGA放大系数谱的预测方程,分析统计结果的离散性。结果表明:PGA放大系数谱受场地条件影响较小,受主余震相对强度影响显著;放大系数谱值随周期增大而减小。谱预测方程能够提供目标损伤下结构的主震PGA放大需求,并可以作为设计谱调整系数使用,以实现在结构抗震设计及结构损伤评估中考虑余震的影响。
关键词:主余震序列型地震动; 单自由度体系; 峰值加速度; 相对强度
中图分类号: P315 文献标志码:A 文章编号: 1000-0844(2024)03-0584-09
DOI:10.20000/j.1000-0844.20220508001
PGA amplification factor spectrum of mainshock-aftershock sequence-type ground motions based on equal damage
YONG Fei1,2, GONG Maosheng1,2, YANG You3
(1. Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute ofEngineering Mechanics, CEA, Harbin 150080, Heilongjiang, China;2. Key Laboratory of Earthquake Disaster Mitigation, Ministry of Emergency Management, Harbin 150080, Heilongjiang, China;3. China Municipal Engineering Central South Design and Research Institute Co., Ltd., Nanchang 330000, Jiangxi, China)
Abstract: Strong aftershocks often occur after earthquakes, increasing the extent of structural damage. Thus, the influence of aftershocks on structures in seismic design and structural damage assessment is an important topic. In this study, the NGA-West2 database was used in establishing the date set of mainshock-aftershock sequence-type ground motions. Based on damage equivalence theory, the peak ground acceleration (PGA) amplification factor under mainshock-aftershock ground motions was defined. Then, the average PGA amplification factor spectra of the structure with a single degree of freedom system under different relative intensities and different site conditions were obtained through dynamic time-history analysis. The prediction equation of the PGA amplification factor spectrum was constructed through regression analysis, and the discreteness of the statistical results was analyzed. Results show that the PGA amplification factor spectrum is less affected by site conditions but affected by the relative intensity of mainshock-aftershock ground motions, and the value of the amplification factor spectrum decreases with increasing period. The spectral prediction equation can provide the PGA amplification requirement of the mainshock under target damage, and it can be used as the adjustment coefficient of a design spectrum. In addition, this equation considers the influence of aftershocks in a seismic design and structural damage assessment of a structure.
Keywords:mainshock-aftershock sequence-type ground motion; single degree of freedom system; peak ground acceleration; relative intensity
0 引言
历次大地震表明,强震发生后往往伴随着多次余震发生,有些余震震级还较大[1-2],如1999年9月21日我国台湾集集发生7.6级地震后,一周内又发生多次较大余震[2];2010年9月年新西兰Christchurch发生7.1级地震没有造成人员伤亡,而2011年2月在同一地区发生的6.3级强余震却造成了146人死亡,300人失踪[3]。强烈的余震会加重工程结构震害,还会影响震后救灾以及结构震后修复和加固成本。一直以来,国内外学者对余震地震动特性和余震对结构响应做了大量研究,包括主余震地震动构造、余震对结构地震响应影响、主余震序列型地震动非弹性反应谱特征等[4-7],通过研究学者普遍认为在结构抗震设計与抗震性能评估中应该考虑余震影响[8-11]。Mahin[12]最早开展了主余震对结构的影响研究,认为不可忽略余震对结构延性和滞回耗能的影响。Li等[13]采用重复法和随机法构造主余震序列,研究钢结构在余震中的倒塌概率,结果表明钢结构在经历强主震后即使遭遇强度小的余震也会发生倒塌。Goda等[14]根据广义大森定律使用衰减法生成余震,研究其对木结构地震响应的影响,发现震级大、峰值加速度高、距离短的余震才会对结构造成额外伤害。于晓辉等[15]对比了上述三种构造方法,发现重复法和随机法构造的主余震序列会比衰减法高估余震的强度,并且会造成较大的增量损伤。Soureshjani等[16]对框架剪力墙结构在地震序列作用下的抗震性能进行了研究,表明主余震能显著增加结构的残余位移和最大相对位移,余震峰值加速度与主震峰值加速度之比是决定框架剪力墙结构地震响应的重要指标。Massumi等[17]研究发现主余震同时考虑地震动竖向和水平分量会增大结构的倒塌概率。刘平等[18]根据“等强代换”原则,对比了主余震序列型地震动作用下配置不同强度钢筋的框架结构抗震性能,发现余震对配置高强钢筋结构的抗倒塌性能有不利影响。Zhai等[19]研究了主余震序列型地震动作用下具有不同滞回模型的单自由度(Single Degree Of Freedom,SDOF)体系非线性响应,得出强余震对非退化系统响应需求影响比退化系统更明显的结论。Goda 等[20]研究认为,真实主余震地震动记录不完整会低估其对结构的影响。Pirooz等[21]研究了主震及其余震间的时间间隔,给出了时间间隔关于自振周期和强震持时函数,以确定结构在主震结束后停止自由振动所需的时间。杜云霞[22]研究表明尽管第二次地震作用较小,3层框架结构经历两次地震作用的累积损伤却十分明显。
上述研究表明,余震对结构抗震性能及破坏状态有着不可忽略的影响,更需要在结构设计阶段予以充分考虑。针对此问题,本文提出了一种考虑余震影响的抗震设计谱修正方法,可以用于抗震设计谱修正及考虑余震影响对结构进行抗震设计。首先,根据实际发生的地震及其余震,筛选出了主余震型序列地震动;然后,基于单次主震作用下和主余震作用下结构损伤相等的思想,定义了峰值加速度(PGA)放大系数,并对不同周期SDOF结构进行了非线性时程反应分析,通过调整主震峰值加速度使得主震作用下和主余震作用下结构损伤相等,得到主震PGA放大系数谱;最后,统计建立了放大系数谱预测方程,并分析了地震动随机性对PGA放大系数及其离散性影响。放大系数谱预测方程可以作为设计谱调整系数,进而可以实现在结构抗震设计中考虑余震对结构的影响。
1 主余震序列型地震动
为了得到研究需要的实际地震中主余震序列型地震动记录,根据文献[23]对主余震序列型地震划分标准,从太平洋地震工程研究中心的强震记录数据库(NGA-West2)(http://peer.berkeley.edu/nga/)选取了9次主震事件及其18次余震事件,选取原则为:(1)主震和余震的矩震级MW均大于5.0,且震级之差在0~2.4之间;(2)主震地震动记录和余震地震动记录均来自同一台站;(3)主震地震动记录和余震地震动记录的两个水平分量PGA均值大于0.04g,峰值速度(PGV)均值大于1 cm/s;(4)台站所在场地的剪切波速vS30在100~1 000 m/s之间;(5)一个台站记录到多次余震时,只选取震级最大的余震地震动记录;(6)地震序列时间定为从主震发生起3个月内。
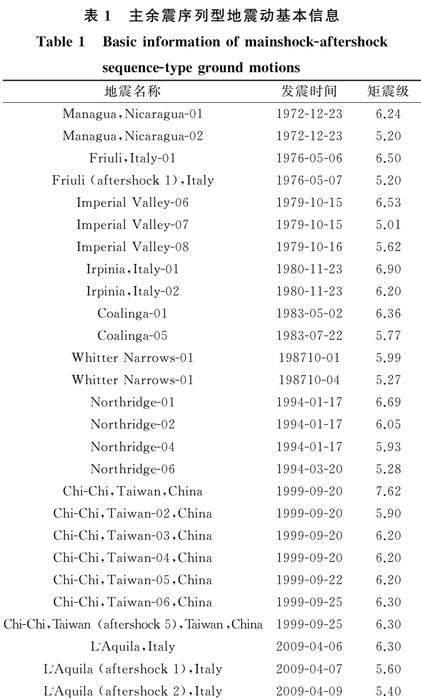
根据上述筛选原则,共选取了286个台站记录到的594条主震地震动记录和594条余震地震动记录,将每一个台站的主震地震动记录及其对应余震地震动记录拼接构成主余震序列地震动记录,共得到594条主余震地震动记录。表1给出了根据上述原则选取的主余震序列型地震动基本信息。数据集包含了286个台站,台站所在场地剪切波速的分布情况如图1所示,vS30在150~850 m/s之间。因为NGA-West2数据库只给出场地的等效剪切波速vS30,根据文献[24]建议,将594条主余震地震动记录按我国抗震规范场地分类方法分为Ⅰ类、Ⅱ类和Ⅲ类,表2给出了这三类场地的地震动数量。地震震级(矩震级MW)-断层距(Rrup)分布如图2所示。图3给出了台站CHY-035记录到的主震记录和余震记录拼接后得到的主余震地震动记录,结构进行地震反应分析时在主震和余震之间增加了60 s的时间间隔,以保证结构在主震后有充分的时间达到新的平衡位置。
2 PGA放大系数
本节针对单自由度体系结构,基于损伤等效思想定义PGA放大系数,以此作为地震影响系数调整值以在结构抗震时考虑余震影响。
2.1 PGA放大系数及其计算方法
计算PGA放大系数的方法是基于调幅后主震地震动作用下结构损伤和未调幅主余震序列型地震动作用下结构损伤相等的思想[25]:通过不断提高主震地震动PGA使得结构经历主震后损伤状态(DIm)与经历主余震序列型地震动后损伤状态(DIseq)相等,计算提高后的主震PGA与提高前主震PGA的比值,如式(1)所示:
α=PGA调整后PGA调整前 (1)
式中:α表示PGA放大系数;PGA调整后为DIm与DIseq相等时的主震地震动PGA,PGA调整前为提高前的主震地震动PGA。为了研究余震对PGA放大系数的影响,用余震地震动峰值加速度(PGAa)与主震地震动峰值加速度(PGAm)的比值PGAa/PGAm表示主余震的相对强度,通过调幅余震使得主余震地震动相对强度达到0.2、0.4、0.6、0.8和1.0。值得说明的是,相对强度表征的是余震相对主震的强弱程度,并非单个地震动的强弱。
PGA放大系数的意义在于:可以在一定程度上反映余震对结构的影响。对地震反应分析而言,在获取余震地震动记录困难或缺少余震地震动记录的情况下,PGA放大系数可以从损伤等效角度使主震地震动替代主余震地震动来分析地震响应;对结构抗震设计而言,PGA放大系数能够量化结构在主余震地震动作用下的PGA增大需求,并且作为设计谱调整系数使用,在设计阶段将余震对结构影响纳入地震影响系数中。图4给出了计算PGA放大系數流程,具体计算过程如下:
(1) 将主震地震动记录和主余震地震动记录的主震部分调幅至一定水平(以0.2g为例),对余震地震动记录进行调幅,使主余震地震动记录达到不同的相对强度(0.2、0.4、0.6、0.8、1.0);
(2) 以主余震序列型地震动为输入对结构进行非线性动力时程分析,计算此时结构损伤指数DIseq,并将DIseq定为目标损伤DIaim,同样的方法得到主震地震动作用下的损伤指数DIm;
(3) 判断DIm是否等于DIaim,若相等则计算α,否则以0.01g的增量提高主震地震动记录的峰值加速度PGAm;
(4) 对提高PGAm后的主震记录再次进行非线性动力时程分析得到此时DIm,重复步骤(3),直到DIm与目标损伤DIaim相等,根据式(1)计算PGA放大系数α值。
在对SDOF体系结构进行时程反应分析时,采用双线性滞回模型,损伤指数采用最为常用的Park-Ang损伤指标,计算SDOF体系在主震和主余震下的损伤指数,通过不断迭代步骤(3)达到预期结果。计算单自由度体系结构损伤指数时,采用双线性本构模型,强度折减系数Ry取4,屈服后刚度取0.02倍初始刚度,周期取0~6 s,其中周期0~2 s间隔0.1 s;2~4 s间隔0.2 s;4~6 s间隔0.4 s。对每个SDOF体系和每条地震动记录分别重复上述步骤(1)~(4),将每条主余震地震动记录及其主震地震动记录计算记为一个工况,那么就能得到35个SDOF体系在594个工况下对应5个相对强度的103 950(594×35×5)个PGA放大系数α,以此作为对PGA放大系数谱进行分析和评价的依据。
2.2 结构损伤指标
在衡量结构地震损伤水平时,需要选取合适的结构损伤指标,目前研究者发展了多个损伤指标模型,包括基于变形、基于能量、基于退化、基于低周疲劳和基于变形与能量的双参数损伤模型等[26],而主余震序列型地震动作用下结构会产生累积损伤[15],这说明损伤指标应该包含累计损伤参数。在对比各类损伤指标后,选取Park-Ang损伤指标进行分析,该损伤指标是双参数模型,在结构损伤评价中被广泛使用。Park-Ang损伤指数计算如式(2)所示:
D=μ-1μu-1+βEhFyXyμu (2)
式中:μu、μ分别为结构在单调荷载下极限延性系数和地震动作用下延性系数;Eh为结构滞回耗能;Fy、Xy分别为结构的屈服强度和屈服位移;参考他人研究结果,无量纲参数β取0.15[27]。
3 影响因素分析
3.1 主余震相对强度
根据图4所示流程计算所得各主余震相对强度下PGA放大系数。图5给出了Ⅰ类、Ⅱ类和Ⅱ类场地不同相对强度下PGA放大系数α的均值。可以看出:PGA放大系数与主余震相对强度有关,随着相对强度增大,Ⅰ、Ⅱ、Ⅲ类场地均值PGA放大系数也增大;相对强度PGAa/PGAm=0.2时,三类场地均值PGA放大系数均接近1.0;相对强度PGAa/PGAm=1.0时,Ⅰ类场地均值PGA放大系数最大可以达到1.21,此时结构在主余震作用下PGA增大需求达到最大,说明地震动相对强度较大的主余震对结构影响显著。
相对强度大于0.4时,短周期段PGA放大系数大于长周期段,表明短周期结构在主余震地震动作用下的PGA增大需求大于长周期结构。对于Ⅰ类场地,场地均值PGA放大系数随着周期的增大而减小,同样的趋势也出现于Ⅱ类、Ⅲ类场地,这里不做赘述。出现上述现象的原因是长周期单自由度体系强度比短周期单自由体系强度低,强度低的结构更容易破坏,因此少量提高主震PGA就能使结构达到目标损伤水平,使PGA放大系数变小。
3.2 场地条件影响
按照Ⅰ类、Ⅱ类、Ⅲ类场地计算所得各类场地的均值放大系数αⅠ、αⅡ、αⅢ,再用各类场地均值放大系数与Ⅰ类场地均值放大系数αⅠ相比,得到归一化的PGA放大系数比αⅠ/αⅠ、αⅡ/αⅠ、αⅢ/αⅠ。本节通过PGA放大系数比来量化场地条件的影响,图6给出了这三类场地在不同相对强度下的放大系数比(以相对强度0.4、0.6为例)。可以看出:场地条件对均值PGA放大系数比基本没有影响。Ⅱ、Ⅲ类场地的αi/αⅠ(i=Ⅱ、Ⅲ)都接近1,且αⅠ/αⅠ、αⅡ/αⅠ、αⅢ/αⅠ的差值都小于5%,说明均值PGA放大系数受场地条件的影响较小,几乎可以忽略。
3.3 离散程度分析
为准确评估结构在主余震地震动作用下PGA放大需求,有必要研究PGA放大系数离散程度的影响因素。结构弹塑性地震响应的离散性与地震输入的随机性有关,地震动统计特征可以描述地震输入的随机性[28],因此,通过相对强度和场地条件来描述地震输入的随机性。变异系数能够比较两组数据的相对离散程度,因此通过变异系数来描述PGA放大系数的离散性。图7给出了不同条件下PGA放大系数谱的离散性,可以看出:PGA放大系数离散性与相对强度和场地条件有关。
由图7(a)、(b)、(c)可知:在同一周期处变异系数随相对强度的增大而增大,表明相对强度越大,PGA放大系数越离散,即PGAa/PGAm=1.0、T=1.5 s时PGA放大系数比PGAa/PGAm=0.8、T=1.5 s时离散。同一相对强度下变异系数先增大后趋于平稳:短周期段变异系数会随着周期增大而增大,表明在短周期段周期越大数据离散程度越大,而长周期段变异系数趋于平稳,说明PGA放大系数在长周期段对周期变化不敏感,与短周期相比,长周期数据离散程度相对稳定。由图7(d)可以看出,与Ⅰ类、Ⅱ类场地变异系数相比,Ⅲ类场地变异系数小,则数据离散程度比Ⅰ类、Ⅱ类场地小;Ⅱ类场地变异系数在大部分周期都介于Ⅰ类和Ⅲ类场地之间,场地越硬数据越离散。图7中变异系数最大值不超过0.3,说明统计数据离散性较小,统计结果可以准确评估结构在主余震地震动作用下PGA增大需求。
4 放大系数谱模型
为了建立不同周期的放大系数谱值,通过回归建立了PGA放大系数谱的预测方程,以此实现在抗震设计中修正规范谱和考虑余震对结构的影响。由前述分析可知,场地条件对PGA放大系数影响不超过5%,且没有随周期变化呈单调递增或单调递减的趋势,因此回归分析中没有区分场地类别。提出的预测方程由如式(3)所示:
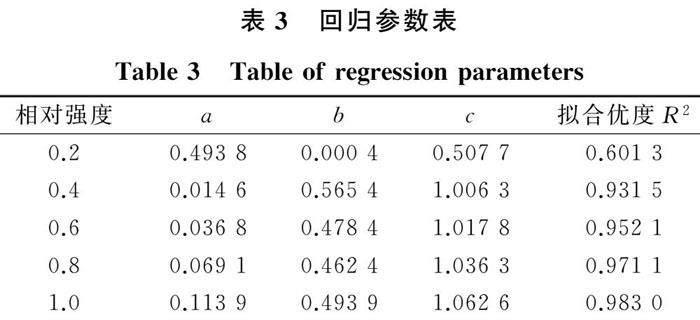
α=a×EXP(-b×T)+c, 0 式中:a、b、c均为回归系数;T为SDOF体系结构周期,回归模型为指数函数与常函数组合形式。通过非线性最小二乘法计算得到回归结果和拟合优度如表3所列。 由表3可知,相对强度(PGAa/PGAm)≥0.4时,该回归模型拟合优度均在0.9以上,最高可达0.983 0,说明PGA放大系数谱拟合程度很好,预测方程能够准确预测放大系数;在PGAa/PGAm=0.2时,回归模型的拟合优度为0.601 3,低于其他4个相对强度的拟合优度,表明此时PGA放大系数预测结果较差,这可能与回归模型有很大关系。回归模型为指数函数与常函数组合形式,在不同相对强度下,回归模型是确定的,且模型中指数部分和常数部分所占的权重均不相同。就各自函数特点而言,常数部分不会随因变量变化而改变自变量;指数部分不然,相对强度为0.2的统计值在整个周期段均近似接近1;而回归模型由于存在指数部分,在自变量T趋近于0时,因变量(拟合值)越大;因此,统计值和拟合值在周期T趋近于0的部分产生了较大的误差。这也是造成拟合优度变小的主要原因,但总体不影响结果适用性,尤其是PGAa/PGAm=0.2时整个周期谱值均接近1(图8),且此时模型与统计结果最大绝对误差在T=0.1 s处,仅为7×10-4,因此以上结果是完全可以接受的。 图8给出了拟合值和统计值的对比,图中可知,PGA放大系数谱有较为统一规律,在同一相对强度下,随着周期增大,放大系数α逐渐减小,最后趋于饱和;在同一周期下,相对强度越大则放大系数越大,即设计谱的调整系数越大。相对强度为0.6、0.8、1.0时,谱形状曲线特征明显,PGA放大系数随周期呈指数衰减,PGA放大系数在短周期段随周期变化敏感,长周期段趋于稳定;相對强度为0.2、0.4时,预测方程虽然为指数函数和常函数组合形式,但是谱形状接近平稳的直线,说明此时PGA放大系数受周期影响小。在整个周期段,相对强度越低,谱曲线越紧密,并且PGA放大系数在相对强度为0.2、0.4时不超过1.05,说明相对强度较低的主余震对PGA放大系数影响小,可以不考虑调整设计谱;随着相对强度的增大,PGA放大系数越来越大,相对强度对PGA放大系数影响越来越明显。 5 结论 本文基于NGA-West2数据库选取了594条主余震序列型地震动记录,对这些地震动记录进行调幅,使其具有不同的相对强度,采用Park-Ang损伤指数来表征结构损伤,计算单自由度体系在目标损伤下PGA放大系数,统计分析了主余震相对强度和场地条件对PGA放大系数及其离散性的影响,根据统计结果构建了PGA放大系数谱及其预测方程。主要结论如下: (1) 场地条件对PGA放大系数的影响可以忽略,而主余震相对强度对PGA放大系数影响较大,主余震相对强度越大对PGA放大系数影响越明显,相对强度较低(PGAa/PGAm≤0.4)的主余震对PGA放大系数的影响较小,小于2.5%。 (2) 相对强度PGAa/PGAm>0.4时,短周期段PGA放大系数大于长周期段,表明余震对短周期结构的影响比长周期结构明显,即考虑主余震时短周期段结构对PGA放大需求要大于长周期结构。 (3) PGA放大系数谱的离散性与相对强度和场地条件均有关,场地越硬、主余震相对强度越大都会增加PGA放大系数的离散程度。 对与PGA放大系数的统计结果,其变异系数不超过0.3,建立的PGA放大系数谱预测方程拟合优度最高可达0.9,统计结果及预测方程可以准确评估结构在主余震地震作用下PGA放大需求。另外,由于Ⅳ类场地主余震序列型地震动记录很少,仅对Ⅰ、Ⅱ、Ⅲ类场地进行了分析,但从结果来看,放大系数谱受场地条件影响很小。因此,对于Ⅳ类场地而言,上述结果也具有一定参考价值。基于等损伤思想建立的PGA放大系数谱,可以用来对抗震设计谱进行调整与修正,以使在结构抗震设计中考虑余震对结构的影响。 参考文献(References) [1] 王泽龙.考虑主余震序列相关性的余震地震危险性分析[D].秦皇岛:燕山大学,2023. WANG Zelong.Analysis of aftershock seismic hazard considering the correlation between main and aftershock sequences[D].Qinhuangdao:Yanshan University,2023. [2] 中国台湾地震工程研究中心.九二一集集大地震震灾调查报告[R].台湾:中国台湾地震工程研究中心,2001. Taiwan Earthquake Engineering Research Center,China.Earthquake disaster investigation report of the 921 Chi-Chi earthquake[R].Taiwan:Taiwan Earthquake Engineering Research Center,China,2001. [3] 张晁军,侯燕燕,胡彬,等.新西兰2010年M7.1地震与2011年M6.3地震活动和灾害分析[J].国际地震动态,2011 (4):44-51. ZHANG Chaojun,HOU Yanyan,HU Bin,et al.Seismic activity and disaster analysis of the 2010 M7.1 earthquake and 2011 M6.3 earthquake in New Zealand[J].International Seismological Trends,2011 (4):44-51. [4] 吴开统,焦远碧,郑大林,等.强震序列对工程建设的影响[J].地震学刊,1987,7(3):1-10,86. WU Kaitong,JIAO Yuanbi,ZHENG Dalin,et al.The influence of strong earthquake sequence on the architectural engineering[J].Journal of Disaster Prevention and Mitigation Engineering,1987,7(3):1-10,86. [5] 温卫平.主余震地震动参数特征及损伤谱研究[D].哈尔滨:哈尔滨工业大学,2015. WEN Weiping.Study on parameter characteristics and damage spectra for mainshock aftershock ground motions[D].Harbin:Harbin Institute of Technology,2015. [6] OMORI F.On the after-shocks of earthquakes[J].Journal of the College of Science,Imperial University of Tokyo,1894,7(2):111-200. [7] DI SARNO L,PUGLIESE F.Effects of mainshock-aftershock sequences on fragility analysis of RC buildings with ageing[J].Engineering Structures,2021,232:111837. [8] 張沛洲,康谨之,欧进萍.主余震序列作用下钢混框架结构损伤与抗震性能分析[J].地震工程与工程振动,2014,34(3):1-8. ZHANG Peizhou,KANG Jinzhi,OU Jinping.Damage and seismic performance analysis of RC frame structures under mainshock-aftershock earthquake sequences[J].Earthquake Engineering and Engineering Dynamics,2014,34(3):1-8. [9] 赵春风,周磊,于娜,等.考虑主余震作用下的核岛厂房结构易损性研究[J].地震工程与工程振动,2021,41(1):113-121. ZHAO Chunfeng,ZHOU Lei,YU Na,et al.Fragility analysis of nuclear island structure under mainshock-aftershock sequences[J].Earthquake Engineering and Engineering Dynamics,2021,41(1):113-121. [10] 韩建平,李军.考虑主余震序列影响的低延性钢筋混凝土框架易损性分析[J].工程力学,2020,37(2):124-133. HAN Jianping,LI Jun.Seismic fragility analysis of low-ductile RC frame accounting for the influence of mainshock-aftershock sequences[J].Engineering Mechanics,2020,37(2):124-133. [11] LUO Q,HE M J,CHEN F,et al.Probabilistic seismic performance assessment of timber-steel hybrid structures subjected to mainshock-aftershock sequences[J].Soil Dynamics and Earthquake Engineering,2021,141:106532. [12] MAHIN S A.Effects of duration and aftershocks on inelastic design earthquakes[C]//Proceedings of the 7th World Conference on Earthquake Engineering.Istanbul:Structural Aspects,1980:677-680. [13] LI Y,SONG R Q,VAN DE LINDT J W.Collapse fragility of steel structures subjected to earthquake mainshock-aftershock sequences[J].Journal of Structural Engineering,2014,140(12):121-132. [14] GODA K,SALAMI M R.Inelastic seismic demand estimation of wood-frame houses subjected to mainshock-aftershock sequences[J].Bulletin of Earthquake Engineering,2014,12(2):855-874. [15] 于晓辉,乔雨蒙,代旷宇,等.主余震序列作用下非线性单自由度体系的增量损伤分析[J].工程力学,2019,36(3):121-130. YU Xiaohui,QIAO Yumeng,DAI Kuangyu,et al.Incremental damage analysis of nonlinear single-degree-freedom systems subjected to mainshock-aftershock earthquake sequences[J].Engineering Mechanics,2019,36(3):121-130. [16] SOURESHJANI O K,MASSUMI A.Seismic behavior of RC moment resisting structures with concrete shear wall undermainshock-aftershock seismic sequences[J].Bulletin of Earthquake Engineering,2022,20(2):1087-1114. [17] MASSUMI A,SADEGHI K,GHAEDI H.The effects of mainshock-aftershock in successive earthquakes on the response of RC moment-resisting frames considering the influence of the vertical seismic component[J].Ain Shams Engineering Journal,2021,12(1):393-405. [18] 劉平,王超,张健新.主余震作用下高强钢筋混凝土框架的易损性分析[J].世界地震工程,2022,38(1):20-27. LIU Ping,WANG Chao,ZHANG Jianxin.Fragility analysis of high strength reinforced concrete frame structures subjected to mainshock-aftershock earthquake sequences[J].World Earthquake Engineering,2022,38(1):20-27. [19] ZHAI C H,WEN W P,LI S,et al.The damage investigation of inelastic SDOF structure under the mainshock-aftershock sequence-type ground motions[J].Soil Dynamics and Earthquake Engineering,2014,59:30-41. [20] GODA K,TAYLOR C A.Effects of aftershocks on peak ductility demand due to strong ground motion records from shallow crustal earthquakes[J].Earthquake Engineering & Structural Dynamics,2012,41(15):2311-2330. [21] PIROOZ R M,HABASHI S,MASSUMI A.Required time gap between mainshock and aftershock for dynamic analysis of structures[J].Bulletin of Earthquake Engineering,2021,19(6):2643-2670. [22] 杜云霞.考虑两次地震作用的RC框架结构地震反应分析研究[D].哈尔滨:中国地震局工程力学研究所,2017. DU Yunxia.Study on seismic response of RC frame structure considering two consecutive earthquakes[D].Harbin:Institute of Engineering Mechanics,China Earthquake Administration,2017. [23] 蒋海昆,杨马陵,付虹,等.震后趋势判定参考指南[M].北京:地震出版社,2015. JIANG Haikun,YANG Maling,FU Hong,et al.Reference guide for post-earthquake trend determination[M].Beijing:Seismological Press,2015. [24] 吕红山,赵凤新.适用于中国场地分类的地震动反应谱放大系数[J].地震学报,2007,29(1):67-76. L Hongshan,ZHAO Fengxin.Site coefficients suitable to China site category[J].Acta Seismologica Sinica,2007,29(1):67-76. [25] 管英珺.考虑多次地震作用的设计地震动确定方法研究[D].哈尔滨:中国地震局工程力学研究所,2015. GUAN Yingjun.Research on determination methods of design ground motion considering multi-earthquake events[D].Harbin:Institute of Engineering Mechanics,China Earthquake Administration,2015. [26] 杨游,杨永强,公茂盛,等.建筑结构损伤模型研究综述[C]//第28届全国结构工程学术会议论文集(第Ⅱ册). 南昌:[s.n.],2019:447-455. YANG You,YANG Yongqiang,GONG Maosheng,et al.Research on damage model of building structures[C]//Proceedings of the 28th National Conference on Structural Engineering (Volume Ⅱ).Nanchang:[s.n.],2019:447-455. [27] FAJFAR P.Equivalent ductility factors,taking into account low-cycle fatigue[J].Earthquake Engineering & Structural Dynamics,1992,21(10):837-848. [28] 叶列平,陆新征,马千里,等.屈服后刚度对建筑结构地震响应影响的研究[J].建筑结构学报,2009,30(2):17-29. YE Lieping,LU Xinzheng,MA Qianli,et al.Influence of post-yielding stiffness to seismic response of building structures[J].Journal of Building Structures,2009,30(2):17-29. (本文编辑:任 栋) 基金项目:中国地震局工程力学研究所基本科研业务费专项资助项目(2019A01,2021EEEVL0301);国家自然科学基金项目(52178514) 第一作者简介:雍 飛(1997-),男,硕士研究生,主要从事地震工程研究。E-mail:yongfei_cn@163.com。 通信作者:公茂盛(1976-),男,研究员,主要从事地震工程研究。E-mail:gmshiem@163.com。 雍飞,公茂盛,杨游.基于等损伤的主余震序列型地震动PGA放大系数谱研究[J].地震工程学报,2024,46(3):584-592.DOI:10.20000/j.1000-0844.20220508001 YONG Fei,GONG Maosheng,YANG You.PGA amplification factor spectrum of mainshock-aftershock sequence-type ground motions based on equal damage[J].China Earthquake Engineering Journal,2024,46(3):584-592.DOI:10.20000/j.1000-0844.20220508001

