借助几何直观加强小学数学计算教学中算理理解

刘玉

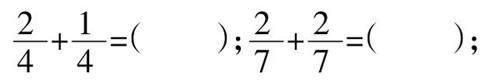
几何直观是指能够准确运用图表描述和分析问题的一种思维方式与学习习惯，对学生学好数学知识有重要意义。在小学阶段的计算教学中，分数计算作为组成部分，需要学生借助几何直观完成知识内容的学习，并且能够通过几何直观完成算理理解，进而扎实掌握分数计算的知识。基于此，在实际教学中，笔者将从深化理解分数概念、认知分数计算意义、有效渗透数学思想等方面入手，阐述如何借助几何直观加强小学数学计算中的算理理解。

一、借助几何直观加强小学数学计算教学中算理理解的要点

（一）有效培养画图能力

在计算教学中，学生不仅需要掌握直接计算算式的能力，还需要具备借助图画分析与解决问题的能力。在此过程中，教师应重视对学生画图能力的培养。对学生而言，画图可以将空间思考的内容，以真实图示的方式呈现，这样可以帮助学生降低学习难度，提高学习效率，实现对问题的有效解决。

（二）重视理解算理过程

在计算教学中，学生要想真正理解计算过程、掌握计算方式，便需要充分重视算理内容的学习。算理是指计算过程中学生的思维方式，主要是解决为什么这样算的问题。掌握算理知识能够帮助学生深化数学内容，看到数学计算教学的本质，从而在根本上提升自身的计算能力。对此，在教学中，教师需要重视对算理理解过程的讲解与分析，帮助学生真正掌握算理知识，提高学生的数学计算能力。

（三）重视教学方法运用

在开展计算教学时，教师需要对几何直观作出有效运用，并通过几何直观带领学生掌握不同的知识内容。这对学生来讲，不仅是在深入掌握计算知识，还是在不断内化几何直观。对教师而言，通过对几何直观的运用，不仅可以转变计算课堂单一讲解的教学方式，还能够提高数学课堂的活跃度，这对提升课堂教学效率有积极意义。

二、借助几何直观加强小学数学计算教学中算理理解的策略

（一）借助几何直观，深化理解分数概念

通过前面知识的学习，学生已对分数的概念有了初步的理解和认知。基于此，在本次课程学习中，教师需要带领学生进一步认识分数计算的相关概念知识，并运用几何直观拆解分数计算，帮助学生熟练掌握分数概念，加深学生对分数计算的理解。

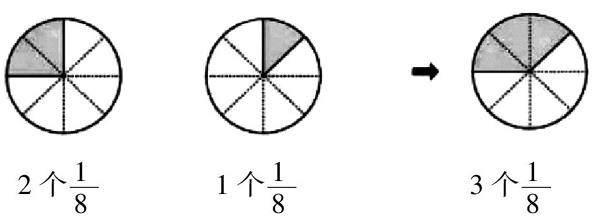
以“分数的简单计算”中的案例1为例。案例1的题干内容是“一个西瓜，哥哥吃了2/8，弟弟吃了1/8。兄弟俩一共吃了这个西瓜的几分之几？”在思考该问题时，教师需要先引导学生思考西瓜共有几块？根据题干中给出的分数信息，学生可以知道一共有8块西瓜，但是，哥哥吃了其中的2块、弟弟吃了其中的1块。由此可知，哥哥和弟弟一共吃了3块西瓜。那么，如何用分数计算出最后的结果呢？这时，教师便需要借助几何直观进行教学分析。首先，教师需要画出三个大小一样的圆，并将其进行8等分。其次，在对应圆形下面标注出对应的分数数值，代表哥哥和弟弟吃掉的西瓜，以及最后共吃西瓜的总数，这样，学生便可以直观地看到哥哥与弟弟一共吃了多少块西瓜。

在理解上述直观图之后，教师便可以用计算的方式，引导学生进行计算学习，即2个1/8加上1个1/8是3个1/8，就是3/8，所以哥哥与弟弟一共吃了3/8块西瓜。在理解上述计算过程时，教师需要引导学生根据分数的基本概念进行计算学习，这样，学生才能理解教师用“2个1/8”表示的含义，进而在分数计算时，因为分子和分母的统一，学生能够根据直观图中的信息获得最后的計算结果。同时，学生还需要掌握2/8是由2个1/8组成的，这样能保证后续计算的顺利，以及让学生理解算理过程。

至此，在认识分数计算知识时，教师需要先带领学生分析分数计算问题的题目，再根据题目画出几何直观图，进而完成对问题的分数计算，获得最后的计算结果。

（二）借助几何直观，认知分数计算意义

在分数计算中，教师既要带领学生掌握分数计算的知识，又要引导学生思考分数计算的意义。基于此，在学习分数计算知识时，教师便可以通过对几何直观的运用，让学生认识到分数计算的意义，从而加强学生对分数计算内容的掌握。

在学习“分数的简单计算”中的案例2时，学生需要计算5/6－2/6=？在计算该分数算式时，学生需要思考，本题目与上一题目之间有何关联，如两个分数的分母相同，都可以进行形式的转变，即如果用分数算理的方式表示，便可以写成5个1/6、2个1/6。基于此，教师可以让学生尝试用几何直观的方法表示上述两个分数。在表示过程中，学生需要注意表示图形前后的一致性。具体而言，学生可以选用6等分的长方形进行分数表示，先画出被减数占据的5个小长方形，再画出减掉2个小长方形后的等分图形。在画出的图形中，学生需要按照步骤，在图形下方记录分数的构成。

根据观察上述直观图形，学生可以清晰地知晓被减数5/6与减数2/6之间的数量关系，可以计算得到的结果是3/6。而根据对长方形等分的情况来看，该分数计算的意义在于被均分的小长方形格子的减少，以及代表被减数数值的降低。（在此基础上，为了让学生及时巩固对分数加法和减法的计算，教师可以指导学生完成教材第98页练习二十一的第1题。在第1题中，分别设计到上一小节分析的分数加法内容，以及本小节分析的分数减法内容。同时，三个小例题在呈现形式上也是以圆形、长方形为主，并且增加了用线段表示分数关系的方法，这种方法学生可以在完全掌握后，进行知识的迁移运用。）

至此，在带领学生讲解分数计算知识时，教师引导学生从算理方面和图形拆解方面体会了分数计算的意义，且学生应做到熟练进行分数减法的计算，锻炼自己的分数计算能力。

（三）借助几何直观，有效渗透数学思想

在学习“分数的简单计算”知识时，笔者通过前两个小节的分析，带领学生学习了关于分数计算的加法与减法。在学习中，学生应注意到一个问题，即不论是分数加法计算，还是减法计算，其分母都是相同的。对此，我们总结出“同分母分数相加减，分母不变，分子相加减”的规律。教师在带领学生完成对前面内容的总结后，便可为学生列举一些计算案例，让学生运用几何直观的方法巩固所学知识，加深学生对数学思想的认知。

比如，教材练习二十一中的第2题。在这一题目中，学生需要计算的题目有：

在计算时，学生需要选择合适的直观图形画出计算过程，并做好算理内容标注。在选择图形时，学生可以选择最常见的圆形、长方形等，既可以做到清晰表示，又可以准确呈现算理内容，能够有效帮助学生巩固所学知识。

在上述教学中，教师借助对前面两小节知识的总结，让学生知晓了同分母分数相加减的计算规律，同时引导学生观察已经计算过的分数算式，让学生意识到其中蕴含的数学思想，以此完成渗透数学思想的目的。

（四）借助几何直观，培养数学空间意识

在学习“分数的简单计算”中的案例3时，教师给出了以整数1为被减数的分数计算算式，且学生需要思考如何运用整数1完成分数计算。在思考中，学生可以观察教材第97页给出的分解计算流程。在图示中，可以将整个圆看作被减数1，根据减数1/4可知，可以对整个圆进行4等分处理，这样，被减数1就变成了4/4，即1-1/4的算式变成了两个同分母分数相减。在计算中，学生可以按照算理的方式，分别标出4个1/4和1个1/4的分数数值，而后再进行计算，便可以得出最终的计算结果。在回顾该分数计算过程中，教师可以指导学生总结计算规律，即计算1减几分之几时，可以先把1改写成与减数分母相同的分数，再根据同分母分数的减法计算，这样，学生便可以降低计算难度，准确无误地完成分数计算。当学生熟练运用几何直观解决分数问题时，学生可以转变运用方法，直接在头脑中对分数进行算理处理，一方面可以提高计算效率，另一方面可以培养空间意识，有助于为后续数学知识的学习筑牢基础。

因此，在运用几何直观进行分数计算学习时，学生不仅要提高自身的分数计算能力，还要借助几何直观培养自身的空间想象力，这样便可以在扎实掌握算理知识的同时，提升自身的数学综合能力。

（五）借助几何直观，加强算理实践运用

在学习“分数的简单计算”时，前面小节的内容分别阐述了关于分數计算加法、减法、被减数为1的加减法的知识内容。基于此，学生需要根据自己所掌握的知识，对其进行实践运用，完成练习二十一中除了第1题、第2题以外的所有题目。在计算中，学生需要做到两点计算要求：第一，运用几何直观清晰呈现计算过程。第二，对计算中的分数进行算理处理，并标注在对应图形下方。如在计算第3题时，题干中已经给出了几何直观的信息，即长方形。因此，学生可以根据题干中的信息，对长方形进行8等分，并分别画出两个大小相等的长方形，分别表示1个1/8和3个1/8，并按照同分母分数的计算方式，完成最后的计算。再比如，计算第5题时，学生应认识到该题目是加减混合计算题。故学生需要先根据给出的信息，算出已经涂上颜色的部分占据长方形纸张的几分之几，再按照整数为1的分数计算方法完成后续的计算。在计算本题目的加法部分时，学生便可以在头脑中思考计算过程，即1个1/10加上3个1/10，是4个1/10。而后根据分数计算方法，将整数1转换为分母为10的分数，即10/10，再进行算理形式的计算，即10个1/10去掉4个1/10，还剩下6个1/10，这样便可以算出未涂色部分占据整张纸的6/10。同理，在计算其他题目时，学生也需要辨别是分数加法，还是减法，或是加减混合计算，然后按照学习的分数计算知识和算理内容准确计算。

至此，在实践运用中，学生应具备有效运用几何直观、分数计算、算理等知识的能力，并能够对其进行融合使用，以做到有效解决数学问题，提升数学综合能力。

（作者单位：兰州市城关区和政路小学）

编辑：赵文静