小学数学解决问题策略的教学实践

叶菲

小学数学教学课堂上，“画线段图”是一种常见的问题解决策略，强调用动手实践的方式将抽象问题具象化，让学生在解决问题的过程中产生“豁然开朗”之感，久而久之提升数学综合素养，为未来学习与发展提供坚实的保障。

一、线段长度的比较

人教版二年级数学上册“长度单位”章节课堂教学实录如下。

教师：同学们，在之前的课上我们已经学习了长度单位，老师有一个问题想问大家。现在我手中有两条丝带，一条长度是6厘米，另一条长度是9厘米，谁能告诉我这两条丝带哪个更长？

学生1：我知道！9厘米的那条更长！

教师：答得很好，那么你能告诉老师，你是怎么得出这个答案的吗？

学生1：因为9比6大！

教师：说得非常正确！这就是我们今天要学习的内容——线段长度的比较。

教师：比较两条线段的长短时，我们首先要确保两条线段的长度单位相同，如刚才老师所提问题中，两个比较对象的长度单位都是“厘米”，所以可以直接通过数字大小来判断长短。

教师：（展示不一样长度单位的两组数据：8毫米和1厘米）對于不同长度单位的比较，我们又该用怎样的对比方法呢？

学生2：我觉得可以换算单位，如将1厘米换算为10毫米，再进行比较。

学生3：我觉得可以直接画出线段图，就能直接比较长短。

教师：那么接下来请同学们试着画出线段图吧。

（学生拿出工具开始画线段图。）

教师巡视，了解学生实践情况，并予以针对性指导。

教师：看了大家画的线段图，我觉得大家做得非常好！其实比较线段长度并不难，只要了解单位换算的规律并能动手操作，就可以用最直观的方式完成比较。

二、线段长度的加减

人教版二年级数学下册“混合运算”章节的课堂教学实录如下。

教师：丁丁家中一共有30盒酸奶，由于周日要去春游，丁丁拿走了12盒，周一早晨爸爸、妈妈、丁丁又各自喝了1盒，同学们，你们知道丁丁家里还有多少盒酸奶吗？

学生1：我觉得可以列出一个计算式，用总数按顺序减去被带走和喝掉的酸奶数量，最后结果肯定正确。

学生2：我觉得可以将带走的与喝了的酸奶数相加，然后用原来的总数减去相加数，就能得到结果。

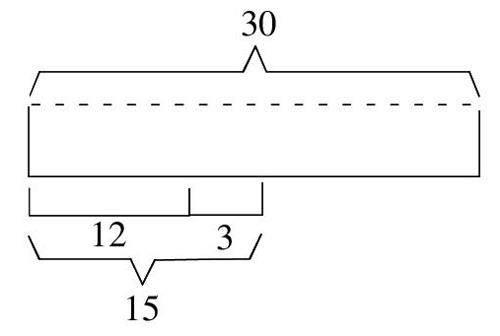
教师：这两名同学说的解决方法都正确，学生1的方法可以总结为“30-12-3”，学生2的方法则可以列出“30-（12+3）”的式子，这两种方法其实都是混合运算，为了更好地解决这一问题，我们可以使用线段图来进行辅助分析，用线段图可以更直观地看到酸奶数量的变化，从而解决问题。

教师：现在，大家尝试自己画线段图，计算剩余酸奶数量，并告诉老师你们总结出的混合运算规律。

（学生开始画线段图，教师随机请学生上台展示并讲解。）

学生3：我要用线段图来表示这个问题。我们可以把丁丁家原来的酸奶数量画成一条线段，表示总数30盒。然后，我们从这条线段上减去周日丁丁拿走的12盒，再减去周一早晨三个人喝的3盒。

学生3：这时如果按照“30-12-3”来计算，就是依次将12和3的部分从线段中减掉，如果按照“30-（12+3）”来计算，则将12与3两部分在线段中视为一个整体，先计算12+3=15，再计算30-15=15，得出正确答案。

教学过程中，教师将“画线段图”问题解决方法融入其中，首先降低了教学难度，对于复杂的“混合运算”，学生也能清晰地探索步骤，并且在亲自动手画线段图的过程中，课堂气氛也会更活跃。学生能在实践中总结数学规律，还能产生成就感，最终在潜移默化中加强对运算顺序的认知，也养成用画线段图的方式解决问题的良好习惯。

三、画线段图解决逻辑推理问题

课堂实录一：

教师：小航和小欣一共有56张“蜡笔小新”的纪念卡片，已知小航比小欣多8张，大家可以算出两人各有多少张吗？

教师：对于这个问题，同学们能想到什么解决策略呢？

学生1：我觉得画线段图可以直接对比出来。

教师：说得很好，我们之前就学习过“画线段图”问题解决方法，那么谁能说一说，对于这道题应该怎样画线段图推理呢？

学生2：将小航和小欣的纪念卡片数量看成两条独立的线段。

学生3：但小航的线段一定要比小欣的线段长。

教师：为什么一定要小航的线段长一点呢？

学生4：因为小航拥有的卡片数量比小欣的多，所以自然要更长一点。

教师：那么小航比小欣线段中多出来的一段代表了什么？

学生5：代表了8张卡片。

教师：同学们说得非常好，既然可以用画线段图的方式推理这个问题，那么我们就一起动手画一画，再想一想、算一算吧，看看谁最后得出的结果正确。

（学生按已确定的思路画线段图，并在观察图的过程中进行逻辑推理，对最终结果进行准确计算。）

教师展示两位学生的线段图。

教师：这两位同学画出的线段图有什么不同？

学生8：学生7画的线段图更清晰，而且能一眼看出去掉小航多出的8张外，小航与小欣的数量是相等的，所以计算也更方便。

教师：是的，学生6画的线段图虽然信息很全，但是线段长短的对比不明显，学生7画的图更直观，不仅能清晰地拆解题意，还能让计算更有逻辑性。

教师：接下来我们根据线段图完成计算吧！算一算小航与小欣各有多少张卡片？

课堂实录二：

教师：甲、乙、丙三人中，甲比乙高，乙比丙高，那么谁最高？这一问题也可以用画线段图的方式来解决，同学们知道该怎么画吗？

学生1：可以将甲的线段画得比乙的线段长。

学生2：题目还告诉我们乙比丙高，所以乙的线段应该比丙的线段长。

教师：大家说得都很正确，那么现在大家尝试画图，然后告诉老师，这三人中谁最高。

（学生开始实践操作）

学生3：甲最高。

教师：能说一说你的判断依据吗？

学生3：我在纸上画出了三条线段，分别代表甲、乙、丙三人的身高。首先，先画出两条长度相同的直线，分别是甲和乙，由于甲比乙高，所以延长甲的直线，再定点变为线段，之后确定代表乙线段的长度，在此基础上再画出一条比乙线段还短的线段代表丙，从而看出来三人中甲最高。

教师：说得真不错。以后再遇到类似的逻辑推理问题，同学们也可以通过画线段图的方法来解决问题。

四、線段的组合与分割

人教版三年级数学上册“倍的认知”章节利用“画线段图”问题解决方法展开教学的课堂实录。

教师：同学们，我们今天要学习一个新的数学概念——“倍”，你们知道这一概念是什么意思吗？

（进入概念解析）

教师：我们已经了解“倍”的基础概念，老师出道题大家来回答：红红有6根香蕉、3个苹果，那么香蕉的数量是苹果的多少倍呢？

学生：香蕉的数量是苹果的2倍。

教师：你是怎样得出这一结果的呢？

学生：我列出计算式“6÷3”，最后得出2，所以判断香蕉的数量是苹果的2倍。

（教师在黑板上画出两条线段，分别代表3和6，让学生进行更直观的对比，深化学生对概念的认知。）

教师：看来同学们已经熟练掌握了“倍”的基础概念，那么我们一起来解决一个实际问题吧。

（PPT出示问题：已知阿宁有3支自动铅笔，而小阳的自动铅笔数量是她的3倍，请问小阳有多少支自动铅笔？）

教师引导学生用画线段图的方式分析题目，将第一个已知条件中“3支自动铅笔”视为一个整体，画出一条线段，再对第二个已知条件“小阳的自动铅笔数量是她的3倍”进行分析，在第一条线段下方画出三条一样的线段，以此表示小阳的自动铅笔数量，通过这样的方式得出最后答案（小阳的自动铅笔数量是阿宁的3倍，所以他有9支自动铅笔）。

五、线段图解决行程问题

教师：同学们，本课我们需要了解速度、时间以及距离之间的关系。这个问题较为复杂，为了方便大家理解知识并深刻记忆，老师将会利用画线段图的方法展开教学。

（教师示范画图）

教师：假设李璐每天从家走到学校需要10分钟，她的速度是每分钟走60米，我们先用一条线段来表示她走的总路程，线段的长度就是用速度乘以时间得出的，即将10×60=600（米）

教师：大家已经对基础概念有了较深的理解，现在问题的难度升级。如果两个人走在同一条路上，一个人走得快，一个人走得慢，在走得快的人晚出发的情况下是否能追上走得慢的人呢？

学生：我们可以用线段表示，计算两个人在相同距离中走路的总时长，再进行对比分析，就能知道是否追得上了。

教师：这个思路是对的，我们现在来解决实际问题。假设小明和小华在同一条路上跑步，小明的速度是每分钟跑100米，小华的速度是每分钟跑80米。小明比小华晚出门2分钟，小明想要追上小华需要计算什么？

学生：需要计算他们之间的路程差和速度差，用路程差除以速度差。

教师：请同学们借助画线段图的方法画一画、算一算，看看小明多久才能追上小华。

（学生开始动手实践，将已知条件画出，分析各个变量）

学生：小明和小华之间的速度差也能用线段代替，通过对线段长度的加减以及对线段的组合，我们能求出最后的数字。

教师：同学们已经具备了运用“画线段图”的方法解决问题的能力，线段图中我们能更清晰地理解“速度差”与“路程差”的概念，从而明确计算的思路，最终找出正确的答案。

（本节课知识难度较大，借助画线段图的方法从根本上消除学生的抵触心理，让他们主动参与其中，在师生的良性互动中，成功达成预期的教学效果，也为学生未来更高难度知识的学习与数学核心素养的提升奠定良好基础。）

将“画线段图”问题解决策略应用于教学实践中，教师首先做到了尊重学生的课堂主体地位，在充分激活学生自主探索意识的前提下增加师生、生生之间的互动，学生能遵循自己的认知规律进行主动思考、动手操作，并且在此基础上形成问题意识，未来面对相关类型的题目，自然可以快速使用画线段图的方式寻找答案，不会陷入困境。

（作者单位：连江黄如论中学贵安学校）

编辑：赵文静