汽车起重机液压缸绳排计算方法研究
宋 轶 王振兴 陈旭东 陈 礼 杜玉龙
1 太原重工股份有限公司技术中心 太原 030024 2 大连鼎顶科技服务有限公司 大连 116000
0 引言
汽车起重机根据伸缩臂伸缩方式的不同主要分单缸插销方式和液压缸绳排方式2种[1-5],因工作方式、运动模式不同,受力传递方式也不同。
单缸插销伸缩机构主要应用于100 t以上汽车起重机,承载能力强,但伸缩控制方式复杂、伸缩时间长、技术难度大。起重机通过缸头实现伸缩液压缸与任意伸缩臂的锁死和解锁,实现伸缩臂按顺序的伸臂、缩臂。在吊载过程中,载荷引起的垂直臂节的受力会以剪力、弯矩的形式从臂头依次向下传递,最后传递到基本臂。载荷沿着臂节的轴向力从臂头传到臂节再通过臂销往下传递,最后传递到基本臂。单缸插销伸缩臂的受力传递为逐级传递,方式较为简单。
液压缸绳排起重机主要应用于100 t以下汽车起重机,具有尺寸小、质量轻、同步伸缩快、无极伸缩等优势。液压缸绳排起重机通过滑轮组、绳排实现臂节的同步伸缩,部分可以带载伸缩。在吊载过程中,载荷垂直臂节的剪力、弯矩与单缸插销相同,轴向力则是通过绳排和液压缸进行传递,传递方式复杂。
针对单缸插销传动的研究较多,如对单缸插销传动动力学[6,7]、液压电气控制系统的仿真研究[8,9],伸缩臂截面优化[10]。伸缩缸绳排传动方面的研究较少,张玖[11]通过分析受力传递方式建立了多节臂结构液压缸及钢丝绳的计算数学模型,讨论对强度、刚度、局部稳定性的影响,没有考虑非线性大变形的影响。
以上研究,对液压缸绳排在结构分析中的建模讨论较少,设计计算没有考虑变形的影响。正确的传递受力计算模型对于产品设计尤为关键。滑轮绳排具有2个特殊性:1)滑轮转动是机构不是结构;2)当忽略滑轮的摩擦和传递效率时,滑轮两侧绳排受力相同,这些特殊性导致建模复杂。
本文推导了汽车起重机液压缸+绳排伸缩机构传递受力计算公式,并基于有限元法、多体系统动力学,建立了五节臂的双缸绳排伸缩臂分析模型。通过算例验证了滑轮绳排模型的有效性,讨论了变形对液压缸绳排受力的影响,为液压缸绳排的设计提供准确的计算模型。
1 模型与方法
1.1 液压缸绳排受力计算
汽车起重机主要包含底盘、转台、变幅液压缸、臂架系统。本文研究的是变幅液压缸及臂架系统。
五节臂双缸绳排汽车起重机臂架系统简化力学模型如图1所示,部件包括伸缩臂、变幅液压缸、伸缩液压缸、滑轮绳排、臂头等。如图2所示,其中变幅液压缸的黑色线为缸筒、白虚线为缸杆;5组黑色大横线为伸缩臂节;基本臂内白虚线为伸缩缸1的缸杆,二节臂内白实线为伸缩缸1的缸筒;二节臂内白虚线为伸缩缸2的缸杆,三节臂内白实线为伸缩缸2的缸筒;三节臂臂头的2个虚线圆及连线为滑轮组1;四节臂臂头的2个虚线圆及连线为滑轮组2;五节臂臂头的2个实线圆为臂头上下滑轮;二节臂~五节臂间的细长实线为绳排;各节臂头、臂尾的长方块表示滑块。
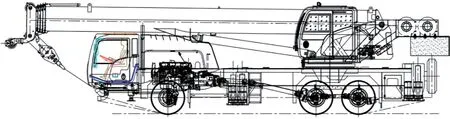
图1 五节臂双缸绳排汽车起重机结构图

图2 五节臂双缸绳排汽车起重机臂架系统简化模型
为方便推导伸缩臂以及滑轮绳排受力的解析公式,做以下假设:1)由于绳排、绳排滑轮组、臂头滑轮组的质量较小,忽略绳排、各滑轮组的质量;2)起升绳方向与五节臂方向相同,即认为起升倍率引起的起升绳向后拉力沿着臂节的轴向方向;3)忽略摩擦力、臂架变形引起的轴向力分布影响;4)由于安装后各节臂的质心水平方向的偏差较小,忽略该差异,假设均处于同一水平线上。
设各节臂的质量为mi,i=1~5。基本臂与二节臂之间的伸缩缸杆、缸筒质量分别为ma1、ma2,二节臂与三节臂之间的伸缩缸杆、缸筒质量分别为mb1、mb2。工况参数包括重力加速度为g、吊载载荷为m、起升绳倍率为k、基本臂变幅角度为α等。
吊载、起升绳、五节臂引起的轴向受力为液压缸绳排2的绳子受力为
液压缸绳排1的受力为2倍液压缸绳排2的受力以及四节臂的重力轴向分量,表示为
将式(1)代入后得
伸缩液压缸2的受力为2倍液压缸绳排1的受力加上伸缩液压缸2缸筒质量、三节臂的重力轴向分量,并减去液压缸绳排2的受力,表示为
将式(1)、式(2)代入后得
伸缩液压缸1的受力为伸缩液压缸1的受力加上伸缩液压缸1缸筒质量、伸缩液压缸2缸杆质量、二节臂的重力轴向分量,减去液压缸绳排1的受力,表示为
将式(2)和式(3)代入后得
以上公式未考虑变形,如果考虑变形,式(1)~式(4)中的α应使用对应臂节所在的角度。各节臂的真实角度计算需要考虑变形,利用有限元法的非线性计算能准确地计算臂节角度。
1.2 梁单元有限元
采用有限元法分析梁弯曲问题时,通常选用的2结点梁单元[12,13]如图3所示。
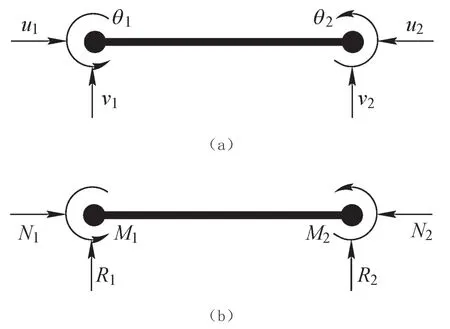
图3 单元节点变形和受力图
图3中,u1、v1、θ1和u2、v2、θ2分别为节点1和2的轴向、切向、转角位移。N1、R1、M1和N2、R2、M2为对应节点1和节点2受到的轴向力、切向力、转角力矩。
梁单元的平衡方程为
其中,C1=AE/L、C2=EI/L3可简写为
式中:Fe为6×1单元力向量,Ke为对称的6×6单元刚度矩阵,qe为6×1单元位移向量。
利用对梁单元局部坐标和整体坐标转换,对单元刚度阵和单元力向量进行刚度矩阵和等效结点力的组集,即得到梁结构系统的有限元平衡方程。组集后可得
式中:K为总体刚度矩阵,q为总体节点位移列阵,F为总体外力列阵。
对平衡方程进行施加边界条件后即可进行线性变形求解。
然而,当结构系统受载后的几何变形较大不满足小变形假设时,此时刚度矩阵、外力列阵不再是常量,而与变形有关,平衡方程可写为
此方程为非线性方程组,总体刚度矩阵K(q)不再是常数矩阵,而是随节点变形改变,总体外力列阵F也与节点变形相关。该方程组可用牛顿-莱夫森法求解或修正的牛顿-莱夫森法进行迭代求解,从而获得大变形非线性解。
1.3 臂架系统有限元模型
为研究变形导致液压缸、绳排的受力差异,建立臂架及液压缸绳排系统有限元模型。利用二维梁有限元对图2的汽车起重机臂架系统进行建模,并进行简化处理说明。
单元说明:1)伸缩臂、液压缸单元均按实际尺寸计算截面面积、抗弯、抗扭截面参数。2)变幅液压缸上铰点到基本臂形心单元、绳排滑轮组单元的截面参数根据尺寸近似计算,并进行放大。
节点说明:1)各节臂臂头、臂尾、中间滑块搭接处为主要节点,基本臂变幅液压缸支撑节点需要从形心处往下偏置,末节臂臂头上下滑轮中心设置节点。2)伸缩缸杆和缸筒头、尾、中间滑动连接处设置为节点;与伸缩臂固定连接的地方,增加伸缩臂的节点;变幅液压缸缸杆和缸筒头、尾、中间滑动连接处设置为节点。3)每个绳排滑轮两侧与绳排相切点、滑轮中心设置为节点,即1个滑轮简化为3个节点。
节点耦合说明:1)变幅液压缸下铰点节点、基本臂根铰点节点与地面转动约束,放开转动自由度。2)变幅液压缸上铰点节点与基本臂连接点节点、三四节臂绳排滑轮中间节点与相应臂头部节点转动耦合,放开转动自由度。3)各节臂相互搭接节点放开轴向移动自由度,耦合其余自由度。4)变幅液压缸、伸缩液压缸中间连接的节点放开沿轴向移动方向的自由度,耦合其余自由度。
按初始变幅角度为0°,即臂架水平放置时建好的有限元模型如图4所示,共包含37个单元,46个节点。其中五节臂单元依次为4、3、3、3、5个单元,共18个单元;3套液压缸共9个单元;2套滑轮绳排共10个单元。

图4 液压缸绳排起重机臂架系统有限元模型
1.4 动力学模型
根据25 t汽车起重机建立的动力学模型如图5所示。模型一共13个物体,3个自由度。其中物体为五节臂、变幅液压缸的缸杆和缸筒、2套伸缩液压缸的缸杆和缸筒,2个滑轮。3个自由度指3个伸缩液压缸的运动,仿真中给定运动学驱动。除了施加重力外,在臂头上滑轮中心施加向后的起升绳拉力(重物质量除以倍率),在下滑轮中心施加竖直向下的重力。

图5 液压缸绳排起重机臂架系统动力学分析模型
滑轮绳排1和2使用Cable子模块建立,如图6和图7所示。第1套滑轮绳排是在三节臂里的伸缩液压缸缸筒头部建立滑轮,在绳排连接的二节臂、四节臂尾部建立绳排锚点。同理第2套滑轮绳排在四节臂头建立滑轮,在绳排连接的三四节臂尾部建立绳排锚点。使用Cable模块建立的绳排滑轮模型,既可体现滑轮的转动、绳子的弹性伸缩,也可保证两侧绳的受力相同,能真实体现实际绳排滑轮的运动学、动力学效果。

图6 动力学模型伸缩绳排1

图7 动力学模型伸缩绳排2
为避免运动过程中动力学惯性力的影响,以较慢速度进行变幅运动控制。采用1 000 s,0.01的步长仿真,仿真完成后进入后处理输出需要时刻或角度的伸缩液压缸受力、绳排受力。
2 算例
以25 t汽车起重机为例进行计算研究。该起重机的伸缩臂、伸缩液压缸的参数如表1、表2所示。

表1 伸缩臂参数
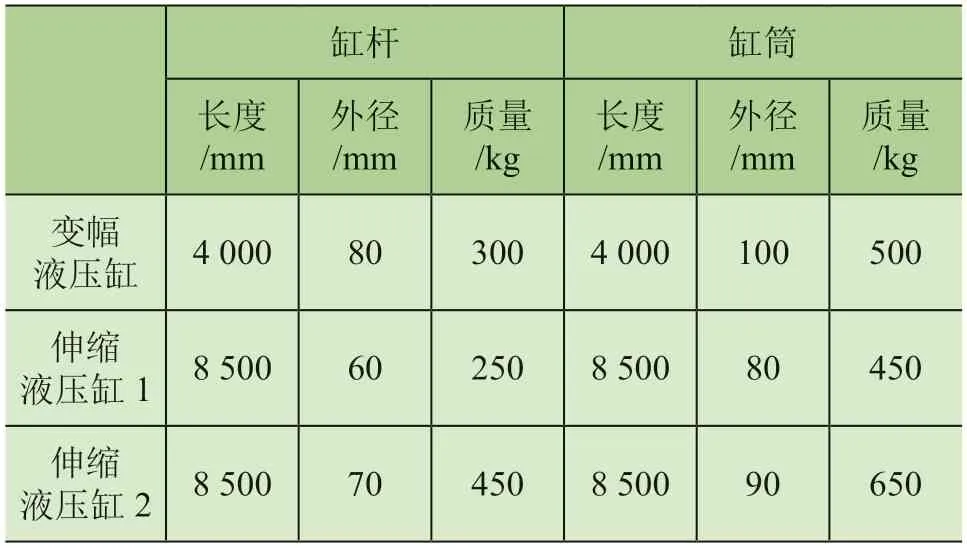
表2 伸缩液压缸参数
2.1 受力计算验证对比
当不考虑变形时,液压缸绳排起重机的液压缸力、绳排力可通过解析公式、动力学模型、有限元模型(把弹性模量增大1 000倍近似刚性)进行计算。为验证模型的一致性,进行算例分析对比。
对比工况为所有臂节50%伸臂,即伸缩液压缸1伸出4.25 m,伸缩液压缸2也伸出4.25 m。臂头吊载5 t,起升绳倍率为2,无风载,有重力。
由图8伸缩液压缸和绳排的受力与臂架变幅角的关系曲线可见,当不考虑臂架变形影响时,3种不同的计算方法的结果曲线基本重合,说明计算方法是等同正确的。
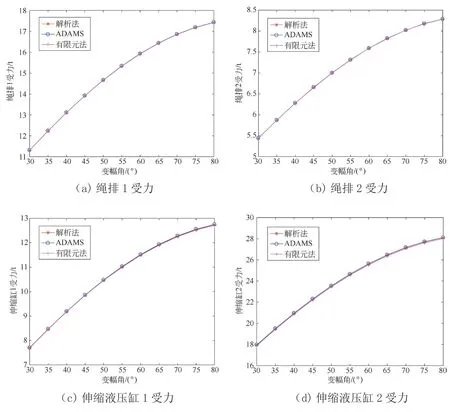
图8 液压缸、绳排受力与变幅角关系
随着变幅角的增加,受力均呈非线性的递增。变幅角小说明臂架接近于水平,重力引起的受力沿着臂架轴向分量小,伸缩液压缸、绳排的受力就小;反之臂架变幅角大说明臂架垂直性大,重力轴向分量大,伸缩液压缸、绳排的受力就大。绳排2受力是绳排1受力的一半,伸缩液压缸2受力是伸缩液压缸1受力的2倍多。
以上分析如解析公式计算、动力学计算均不能考虑变形的影响。利用有限元模型可以考虑变形计算臂架倾斜角度,从而准确地计算液压缸绳排受力。
2.2 考虑变形受力对比
采用有限元模型进行计算,应考虑变形对结果的影响。图9为伸缩臂变幅30°、臂架半伸、吊载5 t、起升倍率为2的变形前后对比图。由于重力作用,臂架由基本臂到臂头渐渐下弯,臂头前探。即整体臂架轴线由于变形前弯的影响由原来的在一条直线上逐渐倾斜。
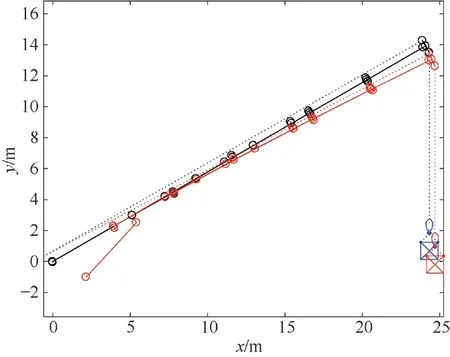
图9 液压缸绳排起重机臂架系统变形前后对比
分析不同变幅角对臂架整体位移变形、弯曲变形、伸缩液压缸受力、绳排受力的影响。图10a和图10b为吊载5 t时臂头位移变形、转角变形与变幅角度的关系。由此可见,随着变幅角的增加,臂头位移变形由0.94 m降到0.25 m,臂头转角由3.2°降到0.7°。即在变幅角度30°时,臂头位移和转角最大。
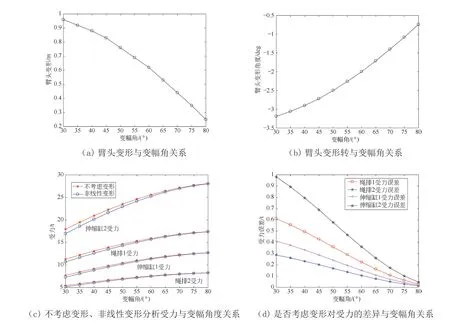
图10 液压缸绳排起重机臂架系统变形前后对比
由于变形影响臂架倾角,进一步会影响液压缸绳排的受力(见图10c和图10d),不考虑臂架变形与考虑变形的受力略有差异。其中伸缩缸2的伸缩力最大差值在变幅角30°时为0.98 t,相对误差为5.5%。
2.3 伸缩臂受力分析
伸缩液压缸、滑轮绳排的分配导致各节臂的轴向力与单缸插销方式有所不同。对同一工况,分析对比2种方式对臂节轴向受力的影响。
图11为五节臂的轴向受力图,x轴为长度单位,用以查看臂长,y轴为轴向受力。每节伸缩臂y方向进行平移处理,方便区分不同臂节。由图11a可见,单缸插销的载荷传递为逐级传递,臂尾到销轴之间均受到吊载载荷和臂节重力的轴向力传递,销轴到臂头承受的该段臂节重力引起的轴向力很小。液压缸绳排对臂节间的轴向力传递如图11b所示,基本臂由于变幅液压缸的影响,变幅液压缸以下,轴向力最大达到46.5 t。伸缩臂每节臂从臂头到臂尾轴向受力均匀,变化很小。四节臂轴向力比其余伸缩臂大。伸缩臂受力均匀是因为绳排由臂尾托着臂节,载荷由臂尾传递到臂头。
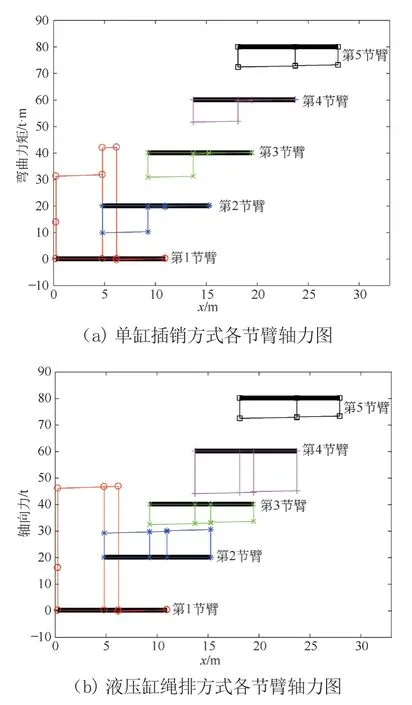
图11 液压缸绳排起重机臂架轴力、弯矩图
3 结论
1)本文建立的液压缸绳排受力计算公式、动力学模型、有限元模型均可用于液压缸绳排的受力计算。解析计算公式更方便,有限元模型计算更准确。
2)变形可减小臂节实际倾斜角度,从而导致轴向受力比不考虑的受力小。随着起重量的增加,变形加剧,影响会变大。
3)伸缩臂节的轴向力与单缸插销有区别,液压缸绳排方式伸缩臂节的轴向受力遍布整个臂节,且分别均匀。

