理解动量守恒定律应注意的四个方面

韦先超

动量守恒定律是自然界中最普遍的基本规律之一，它在解释自然现象和解决实际问题时具有极其广泛的应用。动量守恒定律的表述很简洁，但是同学们不能仅仅局限于记住定律内容（如果一个系统不受外力，或者所受外力的矢量和为0，那么这个系统的总动量保持不变），还需要从以下四个方面着手深刻理解动量守恒定律的内涵和外延，避免因概念理解不透彻、规律认识不清楚而错误应用。

一、选对满足动量守恒定律的系统

由两个或多个相互作用的物体构成的整体叫作一个力学系统，简称系统。利用动量守恒定律列方程式时，既不能把没有参与作用的物体放在选定的研究系统中，也不能在选定研究系统时漏掉参与作用的物体，更不能使得所列方程式两边选定的不是同一个研究系统。

例1 如图1所示，小车和物块位于光滑水平地面上，小球用轻绳悬挂在车厢顶部，某时刻小车以速度v 与静止物块发生碰撞。若小车的质量为m1，小球的质量为m2，物块的质量为m3，碰撞的时间极短，则下列情况可能发生的是（ ）。

A.碰撞后小车、小球、物块的速度均变化，且三者碰后的速度v1、v2、v3 满足关系式（m1+m2）v=m1v1+m2v2+m3v3

B.碰撞后小球的速度不变，小车和物块的速度变化，且二者碰后的速度v1、v2 满足关系式（m1+m2）v=m1v1+m3v2

C.碰撞后小球的速度不变，小车和物块的速度都变为v1，且满足关系式m1v =（m1+m3）v1

D.碰撞后小球和小车的速度变为v1，物块的速度变为v2，且满足关系式（m1+m2）v=（m1+m2）v1+m3v2

解析：小车和物块位于光滑水平地面上，小球悬挂在车厢顶部，由小车、小球和物块组成的系统在水平方向上不受外力作用，可以判断碰撞前后系统的动量守恒。又因碰撞时间极短，小车与物块碰撞的过程中，悬挂小球的轻绳来不及偏离竖直方向，小车与物块间的作用力只能使小车和物块的动量发生变化，而不能使小球的动量发生变化。综上，在小车和物块碰撞的极短时间内，应用动量守恒定律列式时只需选择由小车与物块组成的系统为研究对象。若碰撞后瞬间小车与物块分离，则二者碰后的速度v1、v2 满足关系式m1v=m1v1+m3v2;若碰撞后小车和物块粘在一起运动，则二者碰后的共同速度v1 满足关系式m1v=（m1+m3）v1。

答案：C

注意：小车与物块发生碰撞的时间极短，说明在碰撞过程中，悬挂小球的轻绳来不及摆开一个明显的角度，因而小球在水平方向上尚未受到力的作用，其水平方向的动量未发生变化，即在小车与物块发生碰撞的过程中，参与作用的物体只有小车与物块。

例2 一辆装满细沙的小车以速度v0沿光滑平直轨道匀速行驶，小车（含细沙）的总质量为M 。某时刻在小车底部扎出一个小洞，细沙从洞中不断流出，则小车的速度将（ ）。

A.逐渐减小

B.保持不变

C.逐渐增大

D.条件不足，无法确定

解析：小车沿光滑平直轨道匀速行驶，在水平方向上所受合外力为零，动量守恒。设漏掉质量为Δm 的细沙瞬间，小车的速度变为v'，由于惯性细沙的速度仍为v0，根据水平方向动量守恒得Mv0 = （M -Δm ）v'+Δmv0，解得v'=v0，即小车的速度保持不变。

答案：B

注意：有的同学会列出方程式Mv0 =（M -Δm）v'，得出v'>v0（车速增大）的错误结论，产生这种错误的原因是在利用动量守恒定律列方程式时，没有保持初、末状态研究对象是同一系统（质量不变）这一必要条件。

二、选定同一参考系

四、正确分析临界状态

应用动量守恒定律求解临界问题，需要先正确分析临界状态，抓住临界条件，再考虑矢量性、同一性等列式求解。例如，由轻质弹簧连接的两个物体达到的临界状态是弹簧被压缩到最短或被拉伸到最长，临界条件是弹簧两端的物体速度相等;物体滑上足够长斜面（斜面体可移动）的临界状态是物体滑到斜面的最高点，临界条件是物体与斜面体在水平方向上具有共同速度;以不同运动状态沿水平面同向运动的两个物体的临界状态是后面的物体恰能追上前面的物体，临界条件是后面物体的速度等于前面物体的速度等。

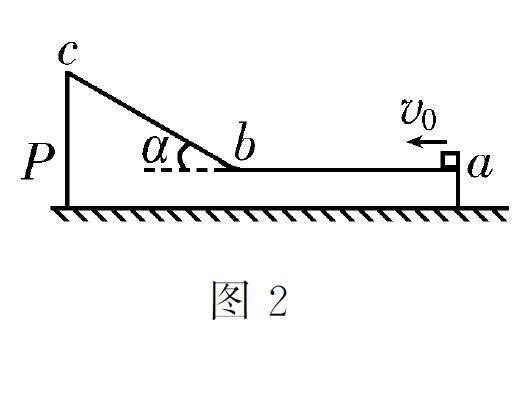
例5 截面如图2所示的物体P 静置于光滑水平地面上，其质量M =2 kg。物体P 截面的水平部分ab 粗糙，长度L=2 m;倾斜部分bc 光滑，倾角α 的余弦cos α=0.4;水平部分ab 和倾斜部分bc 通过一段长度可忽略的光滑圆弧连接。一质量m =1 kg的木块以水平初速度v0=3 m/s从a 点向左运动，沿斜面上升的最大高度h=0.2 m。木块可视为质点，取重力加速度g=10 m/s2，则木块在水平部分ab 上受到的摩擦力f 为（ ） 。

A.1 N B.2/3N

C.1/2N D.1/3N

解析：木塊上升到斜面最大高度处时，若其竖直分速度大于零，则木块会继续上滑;若其竖直分速度小于零，则木块已经开始下滑。

因此木块上升到斜面最大高度处时，达到临界状态，木块的竖直分速度等于零，木块和物体P 沿水平方向具有共同速度。在木块从a点滑至斜面最大高度处的过程中，设木块上升到斜面最大高度处时，木块和物体P 的共同速度为v1，根据动量守恒定律得mv0 =（M +m）v1，根据能量守恒定律得1/2mv20=1/2（M +m）v21+mgh+fL，解得f=1/2N。

答案：C

注意：若对木块上升到斜面最大高度这一临界状态分析不清楚，错误地认为木块上升到斜面最大高度处时，木块的速度为v1，物体P 的速度为v2，得出v2=v1cos α，再根据动量守恒定律和能量守恒定律列式求解，就会得出f=1/3N 的错误结论。

（责任编辑 张 巧）