核心素养视域下“5E”学习环在数学教学中的应用研究
牛伟琪
[摘 要] 核心素养视域下的数学教学,如何利用好“5E”学习环提高教学效率,促使学生深度学习的发生呢?研究者从“5E”学习环的概述出发,以“平行四边形的面积”教学为例,分别从课堂的“借助情境,引入新知”“呈现任务,探索新知”“成果展示,解释新知”“练习拓展,迁移新知”“多元评价,完善新知”等环节开展教学与思考,与同行交流。
[关键词] “5E”学习环;核心素养;探究
实践证明,将“5E”学习环模式应用到小学数学教学中,不仅能帮助学生掌握好“四基与四能”,还能发展其“三会”能力,有效促进其数学核心素养的发展。因此,笔者以“平行四边形的面积”教学为例,具体谈谈如何应用“5E”学习环提升教学效率和发展学生核心素养。
一、“5E”学习环的概述
“5E”学习环是一种以“概念转变理论、建构主义理论、探究式教学”为理论基础自然发展起来的产物,对理科教学有着重要价值与指导意义。如表1,“5E”学习环由“引入、探究、解释、迁移、评价”五个环节组成,每个环节对应不一样的教学目标,对教师与学生分别提出不同的要求。
二、具体措施
1. 借助情境,引入新知
课堂伊始,教师首先要思考如何调动学生学习的积极性与主动性?创设丰富的教学情境往往能快速吸引学生的注意力,激发学习的内驱力,为后续的探究活动奠定基础。实践证明,有效的情境不仅能引发学生的好奇心,激发认知冲突,还能让学生在“愤、悱”的状态下调动学习积极性。
本节课,应用“5E”学习环模式执教“平行四边形的面积”,教师要在“5E”的“引入”环节结合学生认知特征与兴趣点创设能激趣启思的教学情境,以揭示新知,為后续的探究活动奠定基础。
“吸管”是学生经常接触的生活用品,教师可在引入环节借助吸管这个生活实际物品创设情境:用吸管制作长方形,通过对长方形的拉动,引起学生的视觉冲突。
师:观察发现,因吸管制作的长方形经过轻轻拉动就变成了一个平行四边形,你们觉得拉动前后两个图形的面积一样吗?
面对这个问题,学生呈现出不一样的答案。显然,这个情境成功引发了学生的认知冲突,有效激发了学生的探索欲。
师:变形前后两个图形的面积之间存在什么关系吗?如果要计算平行四边形的面积,该怎么办呢?
在问题的启发下,学生表现出浓厚的探索兴趣,教师可趁机引出本节课的教学主题——平行四边形的面积。由此可见,情境引入具有激趣与揭示教学主题的作用,对增强教学效果具有重要意义。
2. 呈现任务,探索新知
在探究环节,教师的任务是提出探究任务并为学生提供充足的探索空间;学生的任务是把握住探究的机会,充分发挥学习的主观能动性,通过对系列探究活动的分析与思考自主提出新的想法,同时将已有的认知迁移到探究过程中,为构建新知奠定基础。在此过程中,教师应关注学生在课堂中的一言一行,做好引导与点拨工作,让探究活动顺利进行。
“让学生亲历平行四边面积公式的推导过程”为本节课教学的重点与难点,也是探究的核心。因此,笔者提出三个探究任务。
探究1:在学生独立思考的基础上进行小组合作学习,分析任意一个平行四边形可转化成什么图形?
学生从自身原有的认知结构出发,结合平行四边形的性质与特点进行图形转化,然后与同伴分享自己的想法。互动中,学生各抒己见,探索氛围和谐、民主。
探究2:学生根据自己的想法,以动手操作的方式将一个平行四边形转化为一个长方形。
学生取出课前用卡纸自制的平行四边形,通过画、剪、拼等方式进行图形的转化。(教师巡视)
探究3:虽然学生转化图形的方法各异,但是都成功了。将转化前后的两个图形放在一起进行对比,它们之间有什么关系?
学生思考并交流,各组学生通过对转化前后图形的观察、对比、分析,逐步获得统一的结论。随着一个个探究任务的提出,学生积极思考,经过“做中学”,亲历了图形转化的过程,有效提升了动手操作能力、直观想象能力、抽象能力等。探究活动基本遵循了先独立分析、后合作交流的模式,学生将个人的智慧融入集体中,在通力合作中协同共进。
3. 成果展示,解释新知
此为“5E”学习环的中间环节,着重关注学生规范、科学的理解与解释新知的情况。教师在此环节要为学生提供充足的时间与空间,为学生的思维搭建“脚手架”,鼓励学生将探究结论展示出来,并尽可能应用规范、完整的数学语言来解释与描述;同时,教师要有针对性地对学生的解释加以点拨与引导,让学生从真正意义上掌握新知,夯实探究成果。
当学生顺利完成三个探究任务后,教师可鼓励学生自主将组内探究成果借助多媒体设备进行投影展示,各小组呈现的方法不一样。
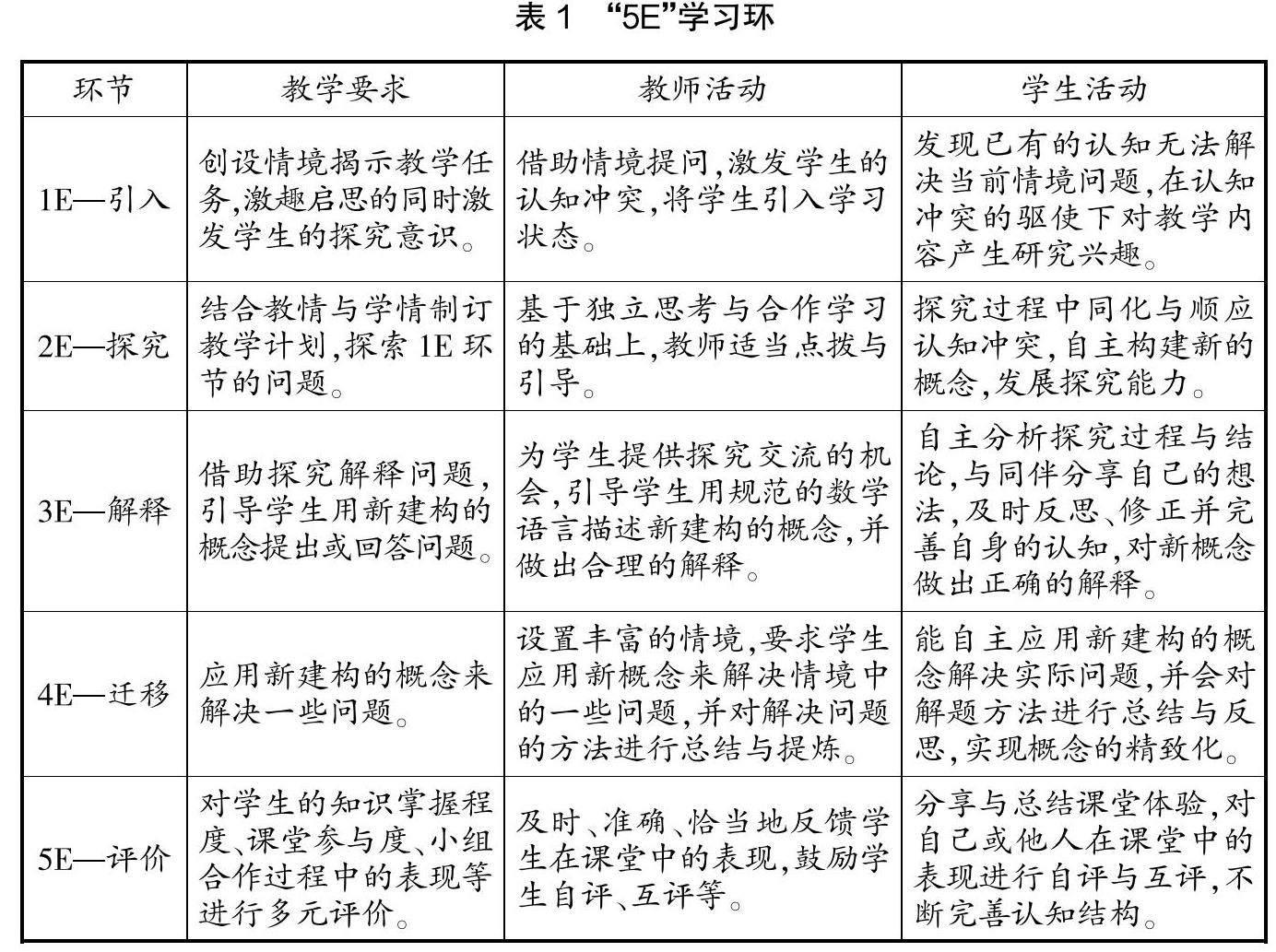
方法1:剪下过平行四边形顶点的高(见图1),把剪下的直角三角形和直角梯形拼接到一起,形成长方形。
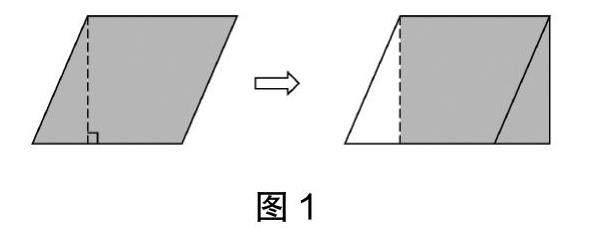
方法2:如图2,剪下平行四边形的任意高,将获得的两个直角梯形进行拼接形成长方形。
方法3:剪下过平行四边形斜边中点的高(见图3),将获得的两个小直角三角形拼接到剩下的图形上,形成长方形。
师:观察这三种拼接方法,可见转化前后的图形之间有哪些条件发生了改变,哪些条件没有发生变化?
生:图形形状都由平行四边形转化成了长方形,即形状发生了改变,但不论用哪种剪拼方式,图形的面积是恒定不变的。
“变与不变”的原理在学生的自主操作中自然生成,据此师生共同推导出平行四边形的面积计算公式。此过程,学生通过动手操作、动脑思考,由浅入深地掌握了平行四边形的面积计算公式,并提炼出一种重要的数学思想——转化思想。此过程可发展学生语言表达能力和逻辑推理能力等。
4. 练习拓展,迁移新知
该环节的关键在于让学生通过解决问题来实现知识的迁移,不断巩固对新知的认识。教师可根据学生的认知水平来组织课堂练习,带领学生结合知识间的联系进行知识的拓展与研究,达到迁移新知与强化认知的效果。
练习训练是迁移新知的重要途径之一。随着系列探究活动的开展,学生获得的体验各不一样,因此对新知也会形成不同程度的认识。学生的个体差异是教师设计练习的主要依据,教师可结合學情设计分层练习,让每个学生都拥有思维训练的机会。本节课,笔者设计了基础练习、提高练习和拓展练习。
(1)基础练习
如图4,请分别计算图中两个平行四边形的面积。
(2)提高练习
校园内有一个平行四边形的花圃,其面积为36m2,高为6m,求该花圃的底边长度。
(3)拓展练习
如图5,为了便于小区内人员的出行,物业中心准备在小区绿化带中铺设一条平行四边形的鹅卵石小路,施工单位提供了三种铺设方案,哪种方案用到的鹅卵石数量最少?
以上三个由浅入深的问题,为每个学生提供了思考的机会,学生尝试应用刚建构的新知来解决这些问题。学生解题后,教师可择取一些具有代表意义的结论进行展示交流。
此过程,学生不仅学会了应用新知解决问题,实现了知识的迁移,还深化了对平行四边形面积的理解,训练了思维。尤其是后两个问题,对发展学生的“三会”能力具有重要意义。
5. 多元评价,完善新知
评价贯穿课堂教学的每个环节。在教学中教师一直在与学生积极互动、交流,其中不乏各种评价与鼓励。恰到好处的课堂反馈与评价是引发学生积极思考、助推探究行为的催化剂,对发展学生的数学核心素养具有重要价值。
本节课,教师立足于学情,进行了客观、积极的评价。在课堂巡视时,教师充分关注了学生的思维状况、动手能力等,并以此为依据提出相应的问题,让教学评价渗透在教学的每个环节。比如,为了了解学情,教师提出:“你们觉得平行四边形的面积可能跟哪些因素有关?”“平行四边形的高越高,它的面积就越大,对不对?”
从学生提供的结论,教师可初步判断学生的认知水平,并据此调整教学方案,想方设法发展学生的“四基与四能”和巩固其认知,为完善其认知结构服务。而学生在多元化评价的课堂中积极探究、乐于解释,收获满满。
三、结语
“5E”学习环的“引入—探究—解释—迁移—评价”各个环节既独立,又具有一定的联系,其中评价贯穿整个教学的始末。如图6,此为一个闭环,引入环节借助情境吸引学生的注意力,让学生积极参与到探究中来;探究环节为解释环节提供思路,可发展学生的创造意识;解释环节进一步完善学生对新知的理解,为知识的迁移应用作铺垫;迁移环节对提升学生的应用意识与推理能力具有重要价值;评价则渗透于每个环节中。
实际教学时,教师不一定要严格按照各个步骤按部就班地依次进行,可结合实际教情与学情,择优选择更科学的方法促使“5E”的流动,以发展学生的数学核心素养。
新课改强调数学教学要关注教学理念、方法与模式的创新,教师应与时俱进加强学习,不断积累教学经验,提高教学实效。“5E”学习环是一种利于学生长久发展的教学方式,与新课改发展数学核心素养的目标一致,值得广大教师去探索研究。

