双尺度粗粒化离散元方法及煤散料试验验证
李 博 ,刘 备 ,张 鹏 ,夏 蕊 ,王学文 ,赵婷婷 ,冯云田,3
(1.太原理工大学 煤矿综采装备山西省重点实验室, 山西 太原 030024;2.太原理工大学 机械与运载工程学院, 山西 太原 030024;3.斯旺西大学辛克维奇计算工程中心, 英国 斯旺西 SA18EN)
0 引 言
离散元法广泛应用于不同领域的颗粒力学行为模拟,包括化学与制药工业[1]、农业[2]以及土木工程[3]等。在煤炭开采[4]、运输[5]与筛分[6]过程中,离散元法被用于分析煤散料与刚性结构间的相互作用,优化机械参数从而提高作业性能。煤散料形状不规则且数量巨大,模拟实际尺寸的煤颗粒系统在计算上非常耗时。普通计算机硬件无法满足计算需求,当前的离散元模拟颗粒数量最多可以达到数千万的水平[7],然而,工业系统通常拥有数万亿颗粒,即使采用GPU 加速也无法满足模拟要求。因此,在工业尺度上使用离散元法模拟大规模煤散料系统仍是一个挑战。煤散料的堆积与运输在煤炭工业现场十分常见,以往学者在进行煤散料系统模拟时,通常使用比实际尺寸大得多的煤颗粒,却并没有明确说明颗粒尺寸选择的依据。
近年来,研究人员在粗粒化理论方面进行了较多研究,以期解决在工程应用中大规模颗粒系统计算的难题。有学者[8-9]提出相似颗粒组合(SPA)模型,并被用于大规模离散元法模拟。在该方法中,具有相似物理或化学特性的颗粒被放大h倍得到粗粒化颗粒。该方法假设粗粒化系统中颗粒的排列方式与原始系统相似,然而,该方法对于控制方程的缩放定律缺乏严格的理论推导,通过假定颗粒大小在颗粒动力行为中起决定性作用,直接将h3作为接触力、液桥力及拖曳力的放大系数。
粗粒化方法更加关注由大多数颗粒引起的集体力学行为,而非个体颗粒轨迹。SAKAI 等[10-12]提出了粗粒化CG 模型(Corse Grain Model),其中粗粒化系统中的颗粒尺寸是原始系统中颗粒尺寸的l倍。该方法假设粗粒化颗粒的动能与原始颗粒动能相同,粗粒化颗粒的平移和旋转运动假设与原始颗粒相同。在粗粒化颗粒的二元碰撞中,作用在颗粒上的接触力为原始颗粒的l3倍。粗粒化系统中的拖曳力和重力按原始颗粒系统的l3倍进行缩放。对于范德华力,粗粒化模型根据能量守恒原理得到其缩放系数为l2。
BIERWISCH 等[13]提出了一种利用量纲分析法构建粗粒化系统的方法,通过构建具有缩放颗粒尺寸的有效介质,使其能够包含与原始系统未缩放颗粒相同的能量密度和能量密度演化。一些学者[14-15]提出了用于模拟颗粒剪切流动的粗粒化方法CGSF(Corse-grained method for granular shear flow),其中滑动摩擦因数、线性刚度系数和恢复系数被缩放以满足能量守恒关系。然而,该方法缩放定律复杂,且模型仅适用于颗粒剪切混合运动,并不适用于所有情况。LU 等[16]提出了一种基于能量最小化多尺度EMMS(energy-minimization multi-scale)的粗粒化模型,它的计算速度比普通离散元计算快几个数量级,并且能充分利用GPU。采用两相分解的EMMS 模型确定粗粒化颗粒的尺寸及固体浓度,以及它们与气流的相互作用力,根据颗粒流动力学理论确定了粗粒化颗粒之间的相互作用。CHU 等[17]在粗粒化系统与真实系统的总能量(包括势能和动能)保持一致的条件下建立了CFD-DEM 耦合下的粗粒化模型用于模拟重介质旋流器中的旋转多相流,通过与原始颗粒的模拟结果进行比较,发现在流体密度较大时,两模型之间的差异很小。Tausendschön 等[18]研究了基于包块的CFD-DPM 流化气固流模拟中颗粒间黏聚力和颗粒间液体传递的粗粒化方法。考虑了4 种不同的粗粒化策略,并通过量纲分析确定了如何缩放与范德华内聚力及颗粒间液桥相关的参数。基于无量纲重叠、应力和有效恢复系数策略产生的粗粒化规则相同,而基于匹配粘结键数的策略则产生不同的规则。程宏旸等[19]利用粗粒化(CG)推导有限元-离散元(FEM-DEM)表面和体积耦合的一般性表达式,对于表面耦合,CG 将耦合力分布到颗粒-单元接触点以外的位置,如相邻的积分点;对于体积耦合,CG 将颗粒尺度的运动均匀化到耦合单元上。
FENG 等[20-21]从普适性角度出发,提出了精确缩尺系统,并推导出精确缩尺系统中颗粒集合各物理量之间应满足的缩放关系。利用该模型,赵婷婷等[22]通过多尺度方法建立了粗粒化系统与原始系统之间的缩放关系,并得到了离散元接触模型中相关参数的缩放定律,但该文仅考虑了圆球形颗粒,且没有与真实试验进行对比。
研究旨在基于精确缩尺系统,建立粗粒化系统与原始系统之间的双尺度缩放关系,并得出离散元接触模型中相关参数的缩放定律,将该方法扩展到三维不规则颗粒系统,为验证粗粒化方法对形状不规则煤散料的适用性,进行了煤散料下落试验以及回转试验,在离散元仿真中采用不同缩放系数的煤颗粒进行了同等条件下的模拟。
1 双尺度粗粒化方法
1.1 精确缩尺系统
图1 描述了原始系统、精确缩尺系统和粗粒化系统之间的关系,其中原始系统为一个由4×4×4 个球形颗粒组成的规则排列,粗粒化系统占据与原始系统相同的几何域。在精确缩尺系统中,相比原始系统,颗粒尺寸和几何域均按照2 倍比例放大。这种精确缩尺使我们能够得到原始系统和缩放颗粒组之间不同物理量的比例关系。然而,精确缩尺同时也会对计算域进行缩放,导致精确缩尺系统中的颗粒数与原始系统中颗粒数相同,无法提高计算效率。因此,在工业规模的颗粒系统模拟中,必须使用粗粒化系统。在推导粗粒化系统的缩放定律前,首先需要了解精确缩尺系统的缩放定律,其主要的推导过程可参考这2 篇文献[20-21],接下来将会简要介绍其推导过程。

图1 3 个系统之间的关系Fig.1 Relationship among the three systems
1.2 精确缩尺系统中颗粒物理量的缩放
若只考虑颗粒的机械运动,那么任何物理量q的大小均可由国际单位制(SI)中3 个基本变量长度[L]、质量[M]和时间[T]的组合推导出来。
然而,对于文献[20-21] 中描述的离散元模型,选择的3 个基本单位变量为:u1—长度[L],u2—时间[T]和u3—密度[ρ],其中只有u3与SI 单位的选择不同。密度的量纲可以表示为[ρ]=ML-3。在SI 单位下,基本单位组合{L,T,ρ}和基本单位组合{L,M,T}的转换矩阵及其逆矩阵为:
在精确缩尺系统中,通常可以独立选择与3 个基本变量相对应的缩放系数,分别为长度h,时间h,密度1,即基本单元转换系数为Hb={h,h, 1}。然后,与精确缩尺系统中任意物理量q对应的缩放系数hq可从基本单元转换系数、转换矩阵的逆R-1推导出来:
以物理量力F为例,在由SI 单位表示的粒子系统中,其量纲为
在基本单位为{L,T,ρ}的精确缩尺系统中,力F的量纲由以下向量表示:
根据公式(2),可以得到精确缩尺系统中力F的缩放系数hF,计算公式如下:
根据上述推导过程,可以计算精确缩尺系统中每个物理量的缩放系数。表1 列出了一些主要的物理量,而其他物理量可以在文献[21]中找到。选择基本缩放系数集合Hb={h,h, 1}可确保精确缩尺系统中的应力、应变、杨氏模量和能量相关性质与原始系统中的相等。

表1 精确缩尺模型中主要物理量的缩放系数Table 1 Scaling factors of main physical quantities in exact scaled model
从表1 可看出,在精确缩尺模型中,时间变量比原始系统大h倍,导致相应的时步放大h倍。因此,当采用中心差分方法进行时间积分时,使用精确缩尺系统并不能提高整体的计算效率,因为两个系统所需的时步数保持不变。另外,对于无量纲系数如摩擦因数、泊松比和阻尼系数等,不需要进行缩放处理。
1.3 粗粒化模型
粗粒化系统与原始系统所占据的几何区域相同。这样可以减少粒子数量,同时仍保留在精确缩尺系统中获得的整体相似规律。以图2 中立方体内包含的颗粒集合作为代表性体积单元(RVE)。为确保粗粒化系统中的离散元计算结果与原始系统的物理力学性质相一致,RVE 在两个系统中需要满足一定条件。具体来说,RVE 必须满足几何一致,并且在质量、动量和能量密度方面满足近似守恒。

图2 原始系统及粗粒化系统中的代表性单元Fig.2 Representative units in original system and coarsegrained system
假设粗粒化系统和原始系统之间存在几何缩放系数h,那么粗粒化RVE 中的粒子数和接触数与原始RVE 中的粒子数N和接触数Nc之间的关系满足:
RVE 边界上的颗粒接触数满足下式,其中Nb和分别为原始RVE 和粗粒化RVE 边界上的颗粒接触数:
动量守恒条件要求:
能量密度守恒包括动能密度守恒、应变能密度守恒和能量耗散率守恒。2 个RVE 粒子系统的平均柯西应力表达式应大致相同,如下所示,其中xk为原始系统中的接触点位置,为粗粒化系统中的接触点位置:
根据方程(7),可推导出两个系统中RVE 边界上接触力的缩放关系:
原始系统中RVE 的整体平动方程为:
从以上分析可以看出,在精确缩尺系统中,接触力的缩放系数与粗粒化系统完全相同。因此,精确缩尺模型中提出的对于不同类型的离散元接触模型的缩放定律可以完全应用于粗粒化系统中的离散元计算。
所提出的“双尺度”为原始系统和粗粒化系统之间存在的两种尺度的缩放关系,粒子间接触力代表了“细观”尺度力,重力、外加力、拖曳力等代表“宏观”尺度力。在粗粒化系统中,细观尺度力的缩放关系与精确缩尺模型的缩放关系一致(h2),而宏观尺度力的缩放系数为h3。
对于时间变量,与细观尺度相关的量(例如时间步长)的缩放系数是h,与宏观尺度相关的量(例如总模拟时间)保持不变。这样就形成了一个双尺度的粗粒化框架。在计算成本方面,将粒子尺寸扩大h倍将使粒子数量减少h3倍,从而使每个时间步的计算效率提高相同的倍数。此外,由于时间步长也扩大了h倍,时间积分步数的总数减少了h倍。因此,粗粒化系统的总时间理论上是原始系统的1/h4。
1.4 煤散料模型
为验证以上双尺度粗粒化方法的正确性,进行了煤散料下落和回转试验,这些试验常用于校准和修正与冲击和输运相关的煤散料参数[23-24]。在仿真过程中,粒子集合的总体积保持不变,只改变煤颗粒尺寸。煤散料的不规则形状用具有相同半径的圆球形颗粒拼接表示,在仿真中考虑采用3 种不同形状的煤颗粒组合用于表示真实煤散料,包括扁平状、类锥状和类块状,如图3 所示。颗粒组合的最大长度用于表示单个煤颗粒尺寸。仿真中采用5 组不同缩放系数的颗粒,见表2,以C-1 为例,煤颗粒模型的最长边尺寸设定为4 mm,总体积为0.001 m3,每种煤颗粒形状占1/3(质量分数)。在其他组的模拟中,保证煤散料总体积为0.001 m3不变,C-2 到C-5 中的煤颗粒通过将C-1 中的等比例放大而得(放大系数分别为1.5、2、2.5 和3)。颗粒尺寸的选取主要是依据进行试验的设备尺寸来定的,颗粒尺寸过大会导致颗粒无法通过相应设备,且颗粒过少无法形成堆积,而颗粒尺寸过小会导致仿真时间急剧增加。

表2 仿真计算条件Table 2 Calculation conditions

图3 煤颗粒模型Fig.3 Model of coal particles
根据笔者课题组对中国陕西省榆林市神木县长焰煤的标定结果,设置了相应的参数见表3[25]。使用Hertz-Mindlin(no slip)模型来模拟煤散料之间以及煤散料与刮板输送机之间的相互作用。从文献[21]可知,在三维离散元计算中,赫兹模型是尺度无关模型,原始系统中使用的接触参数可应用于不同尺度的粗粒化系统。

表3 验证试验所需仿真参数Table 3 Simulation input parameters for verification test
2 煤散料下落试验
2.1 煤散料下落试验装置及仿真模型
研究使用的煤散料下落试验装置如图4a 所示,使用了来自神木县的长焰煤进行试验。试验过程如图4b 所示。压力传感器(DYZ-102)安装在底板下方,并与测力仪表(D800)相连接,其由24V 直流供电,采用RS485 标准与计算机进行通信(图4c)。压力传感器用于测量煤散料下落到底板上的冲击力,而高速摄像机(GC-P100)用于记录煤散料流动形态及试验结束时煤散料堆积形成的休止角。底板上的平均冲击力和休止角度作为表征参数以验证粗粒化离散元模型的准确性。试验进行了3 次,取平均值作为最终测试结果。

图4 煤散料下落试验Fig.4 Coal falling test
仿真中的煤下落试验装置三维模型与真实试验相一致(图4d),煤散料参数与表3 中的参数一致,使用EDEM 软件进行离散元模拟。料斗中的颗粒工厂生成速率设置为5 kg/s,料斗下方的上挡板在t=0.4 s时(煤散料稳定后)以10 m/s 的速度被水平抽出。表2中显示的煤颗粒由料斗中的颗粒工厂生成。将从仿真中获得的平均冲击力和休止角与实际试验结果进行比较,以验证粗粒化离散元模型的准确性。
2.2 仿真与试验结果对比
1)不同时刻煤散料流动形态对比。在试验过程中,使用高速摄像机记录了4 mm 煤颗粒的流动形态。完全脱离漏斗的时刻被视为时刻0。选择了0.1~0.6 s 不同时刻的煤流动形态,并将其与相同尺寸颗粒仿真中对应时刻进行比较。如图5 所示,可以观察到试验和仿真中相同时刻的煤流动形态非常相似。

图5 煤散料流动形态对比Fig.5 Comparison of bulk coal flow patterns
2)冲击力对比。图6a 所示为使用4 mm 煤散料进行真实试验和仿真的冲击力对比。在底板上的最大冲击力发生在煤落下的初始阶段,随后波动逐渐减小直至冲击结束。为比较平均冲击力,对两条曲线进行积分,并除以积分区间的长度得到相应的平均值。真实试验测试中的平均冲击力为5.855 N,而仿真结果显示平均冲击力为6.066 N。仿真和试验值之间的相对误差为3.60%,两者结果非常接近。从图6 还可发现,随着颗粒尺寸的增大,冲击力的波动性变得愈加严重,这是煤散料颗粒尺寸增加导致下落过程中颗粒离散程度变大,从而使底板受到不连续冲击造成的。从图6 中可发现,冲击结束后底板上的真实作用力大于仿真中的,这是由于仿真中使用的煤散料由球形颗粒拼接而成,因此会有更好的流动性,而真实试验中的煤散料形状不规则,流动性偏差,导致底板上堆积的煤散料更多。详细的试验与仿真结果见表4,总体来讲,随着颗粒尺寸的增加,真实试验与仿真之间的平均冲击力相对误差增加,当仿真中煤颗粒尺寸为12 mm 时,误差达到最大(14.36%)。

表4 煤散料下落试验的仿真条件与结果Table 4 Calculation conditions and results of coal falling test
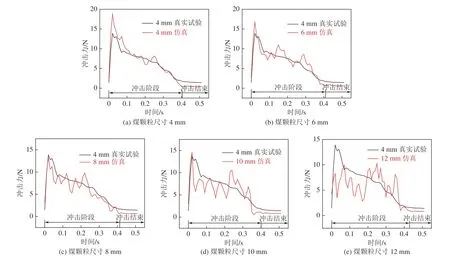
图6 冲击力对比Fig.6 Comparison of impact force
3)休止角对比。在煤散料下落完成后,使用MATLAB 软件对仿真和试验中获得的煤散料堆轮廓进行拟合。如图7a 和表4 所示,真实试验中的煤散料休止角为28.528 5°,仿真中的煤散料休止角为30.634 0°,相对误差为7.38%。图7 对真实试验与仿真堆积轮廓进行了线性拟合(分别为线A与线B)。从表4 可以看出,随着粒子尺寸的增加,休止角并没有明显的变化趋势。从休止角的相对误差可以看出,总体来讲,随着煤颗粒尺寸的增大,相对误差变大。在仿真中,C-2 到C-5 的总计算时间甚至少于预测值(C-1 的1/h4),其原因是模拟中使用的煤颗粒由小的球形颗粒组合而成,为确保每次模拟料斗中的煤散料总体积为0.001 m3,C-2 到C-5 中生成的粒子数量少于计算出的粒子数量(C-1 的1/h3),使得模拟时间减少,计算速度比预期更快。

图7 煤散料堆积轮廓对比Fig.7 Comparison of coal pile profiles
3 煤散料回转试验
3.1 煤散料回转试验装置及仿真模型
煤散料回转试验装置由多个零部件组成,包括机架、料槽、上试样和夹具等(图8a)。机架固定在地面上,料槽由电机驱动旋转。上试样及其附属夹具固定在机架上。上试样的下端倾角为75°,为消除外部作用力的潜在干扰,试验前上试样被抬高1 mm。三向压力传感器(T501)通过夹具连接到机架上,传感器组成如图8b 所示。为创建回转试验装置简化模型,使用UG 软件进行建模(图8c)。为模拟试验过程中煤散料运动行为,将运动子系统添加到动力学软件RecurDyn 中,保持料槽旋转速度恒定(4 rad/s),然后将动力学模型导入EDEM 软件中作为Wall 文件,实现颗粒和刚体运动状态的实时共享。模拟中使用的煤散料体积为0.001 m3,煤散料参数与表2 中一致。总模拟时长设定为2 s,其中前0.5 s 为煤散料生成时间,后1.5 s 为模型运动时间。

图8 煤散料回转试验Fig.8 Coal rotation test
在旋转过程中,煤散料随着料槽的运动与上试样碰撞,在上试样的内侧和外侧形成堆积。模型坐标系如图9a 所示,X轴与上试样的径向对齐,Y轴平行于槽的内侧线。为测量煤散料的横截面曲线,料槽初始位置定为0°,将90°、180°和270°这3 个位置(图9b)的轮廓坐标取平均值,利用MATLAB 进行图像处理和曲线拟合,得到相应的轮廓曲线。在实际测量中,使用直尺测量轮廓位置坐标,每隔10 mm 选择一个点,共9 个点用以拟合轮廓曲线。

图9 煤散料堆积状态Fig.9 Coal accumulation state
3.2 仿真与试验结果对比
1)上试样受力。图10 所示为真实试验及仿真中上试样受力的结果对比。图10a 为上试样在4 mm煤散料作用下的平均力,将曲线积分并除以区间长度,得到相应的力平均值。试验中施加于上试样的平均力为0.560 N,仿真结果为0.596 N,相对误差为6.43%,仿真与试验结果非常接近。如图10 所示,上试样的受力波动随煤颗粒尺寸增加而增加(尤其对于10 mm 和12 mm 的颗粒),这是由于煤颗粒尺寸的增大导致煤散料的离散性变大,导致作用力波动程度变大。仿真中,随着煤颗粒尺寸的增加,作用于上试样的平均力相对误差逐渐增大,具体数据见表5,在误差允许范围内,粗粒化方法可以进行相应过程的模拟。

表5 煤散料旋转试验的仿真条件与结果Table 5 Calculation conditions and results of the rotation test

图10 不同煤颗粒尺寸下上试样受力对比Fig.10 Comparison of force on the upper sample
2)煤散料剖面曲线。图11a 为4 mm 煤散料的试验及仿真剖面堆积轮廓的对比图,轮廓位置通过将90°、180°和270°位置处的数值进行平均得到。水平和垂直坐标是相对于原点的位移(基于图9a 中的坐标系)。通过Matlab 对煤散料剖面曲线进行拟合,试验和仿真数据的相关系数R分别为0.950 和0.936 3,比较试验和仿真剖面曲线,得到其相关系数为0.989 8,表明两者之间的煤颗粒堆积轮廓非常相似。图11为煤颗粒尺寸从4 mm 到12 mm 的煤散料剖面轮廓曲线的比较。总体来讲,随着煤颗粒尺寸逐渐增大,相关系数变小,这可以归因于煤散料的流动性随尺寸增大而减小,相关系数数值见表5。另外,C-2 到C-5 的总模拟时间均少于预测值(C-1 的1/h4),与煤散料下落试验类似。

图11 不同缩放系数下煤散料的轮廓曲线Fig.11 Comparison of coal profile curve
4 结 论
1)利用量纲分析,获得了颗粒系统每个物理量在原始系统和缩尺系统之间的尺度关系,这为离散元接触模型中接触参数的处理提供了理论基础。采用多尺度描述方法,在粗粒化和原始系统之间建立了RVE 单元。通过应用不同系统的RVE 单元之间的质量、动量和能量守恒关系,获得了两个不同尺度(宏观和细观)上的关系。从精确缩尺模型得到的缩放定律在细观尺度上完全适用于粗粒化系统。
2)通过对煤散料下落和回转试验中的冲击力、煤散料休止角、上试样受力和煤堆剖面曲线进行离散元计算,验证了该方法的有效性。在可接受的误差范围内(依据具体问题确定误差范围),粗粒化方法可有效模拟相应的过程,为工程尺度上的大规模离散元计算提供了高效的解决方案。
3)文中研究对象为干煤散料,对于含水煤散料还需要进一步深入研究。尽管文章提出了双尺度系统,但目前还没有理论方法来预测粗粒化和原始系统之间的计算误差,未来需要研究解决这个问题。此外,还需要进一步研究与旋转相关的物理量尺度规律,这在文中没有进行详尽探究。

