基于扰动观测器的终端滑模混沌系统控制
张晓雪,王 成,翟宇凡
(淮南师范学院 金融与数学学院,安徽 淮南 232038)
自从L.M.Pecora 等[1]开创了包括混沌系统同步在内的非线性动力学研究领域以来,有关混沌控制与同步的研究受到了广泛的关注。混沌涉及的领域包括物理、化学、生物、医学、社会经济、信息处理和安全通信[2-3]等。包括反馈线性化、PID 控制、反推控制和终端滑膜控制在内的混沌控制技术已经用于解决混沌同步问题。最近,一些学者利用有限时间控制方法研究了混沌系统的控制问题,取得了许多有价值的成果,例如:S.P.Bhat 等[4]首次提出了非线性系统的有限时间控制方法,并用此方法处理了由终端滑模控制器引起的自适应律抖振问题;SUI S 等[5]运用有限时间控制方法研究了一类非严格反馈系统的稳定性问题。在此基础上,我们为一类不确定二阶混沌系统设计了一种基于扰动观测器的终端滑模控制方法,利用扰动观测器观测外部扰动,通过数值仿真证明扰动估计误差在有限时间内能收敛到零,以此说明控制方法的有效性。
1 系统描述
考虑如下一类二阶混沌系统
其中,x(t)=[x1(t),x2(t)]T∈R2为系统状态,f(t,x(t))∈R为系统未知函数,d(t)∈R为未知在扰动,g(x(t))∈R为已知控制系统增益函数,u(t)∈R为控制输出。
需要说明的是常见的二阶Duffing 系统、二阶水平平台系统和二阶电力系统等都可归结为系统(1)。由于上述系统在给定某些参数条件下会出现有害的混沌现象,故研究系统(1)的稳定性控制具有重要的现实意义。
为了使设计的扰动观测器能够精确估计系统(1)中的未知项组成的混合扰动,使系统(1)的状态x1(t)能够在有限时间跟踪参考信号x d(t),做如下假设。
假设1:系统状态x(t)、参考信号xd(t)以及其导数和是可测函数。
假设2:函数f(t,x(t))和外在扰动d(t)是有界函数。
g(x(t))虽然是已知函数,但在某些时间点可能会出现奇异。为了消除奇异的影响,引入辅助控制器u1(t),且u1(t)满足
其中τ为小的正常数。
将式(2)代入式(1)中,系统(1)可改写为
由假设2 和控制器的有界性可知,存在β>0,使得|D(t)|<β。
2 用到的引理
为了得到本文的结论,先给出两个引理。
引理1:设V(t)为连续正定函数,若对于任意的t>t0,V(t)的导数满足
则V(t)在有限时间ts内到达原点,满足
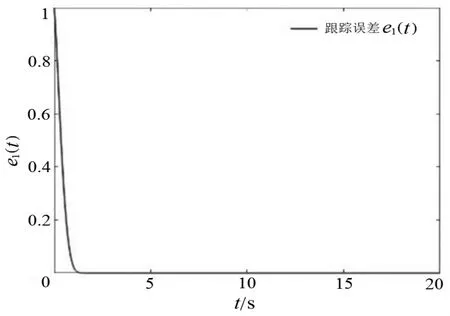
其中,q1和p1为正奇数,且有q1 引理2:若0<γ≤1,a1,a2,…,an≥0,则有 设计扰动观测器为 其中,k1和k2为正的设计参数,c1和c2为正奇数,且c1 其中w(t)的导数为 由式(3)、式(7)、式(8)和式(9)可得 假设跟踪误差为 设计终端滑模流形为 其中,k3和k4为正的设计参数,c1和c2与(7)式中的相同。显然,由式(10)和式(11)可求s(t)的导数 基于上述内容,可设计控制法则 其中k5和k6为正的设计参数。 定理1:若扰动观测器和控制法则分别为式(7)和式(13),则跟踪误差在有限时间能到达原点,且能通过扰动观测器精确估计混合扰动。 证明:假设Lyapunov 函数为 由假设1、假设2 和引理2 可知 现在利用Duffing 振荡模型验证所本文给出方法的有效性。Duffing 振荡模型为 为了证明滑模控制的有效性,分别取控制策略式(7)、式(8)、式(9)和式(13)中的参数为c1=3,c2=5,k1=3,k2=1,β=20,t=0.2,k3=2,k4=3,k5=2,k6=1,取系统初值[x1(0),x2(0)]T=[1,0.2 ]T,在观测器中,取w(0)=0,利用Matlab 进行数值仿真,可得如图1、图2 和图3 所示的结果。 图1 跟踪误差e1(t)随时间的变化情况 图2 混合扰动的精确估计结果 图3 控制输入随时间的变化情况 分别从图1、图2 和图3 可以看出,跟踪误差e1(t)在有限时间到达原点,混合扰动能够被精确有效估计,整个控制输入在初始阶段出现抖动但很快趋于稳定,这说明本文给出的控制方法是有效的。 在本文中,我们研究了二阶非线性混沌系统的跟踪同步问题,并得到以下结论:终端滑模面保证了跟踪误差 在有限时间内到达原点,利用所设计的扰动观测器能够精确有效地估计混合扰动,通过数值仿真证明了方法的可行性。3 控制系统
4 主要结论
5 数值仿真


6 结束语

