与相交线、平行线“面对面”

吴行民

对“相交线与平行线”中一些易错点进行剖析，有助于我们更好地掌握知识，

一、易错概念辨析

1．垂线，如果两条直线相交所成的四个角中的任意一个角等于90°，那么这两条直线互相垂直，其中一条直线叫作另一条直线的垂线，它们的交点叫作垂足．垂线的性质：同一平面内，过一点有且只有一条直线与已知直线垂直：连接直线外一点与直线上各点的所有线段中，垂线段最短，两条直线互相垂直是两条直线相交的一种特殊情况，今后如果遇到兩线段垂直、两射线垂直、线段与射线垂直，都是指它们所在的直线互相垂直．过一点作线段的垂线，垂足可以在线段上，也可以在线段的延长线上．

2．距离，连接两点的线段的长度，叫作这两点的距离．直线外一点到这条直线的垂线段的长度，叫作点到直线的距离．要注意垂线段与距离的区别，距离是一个数量，是指垂线段的长度，垂线段是线段．一定要纠正如“作出点到直线的距离”之类的错误．

3．“三线八角”．两条直线被第三条直线所截，构成八个角，我们看那些没有公共顶点的两个角的关系．当两个角分别在两条直线的同一方，并且都在截线的同侧，这样的一对角叫作同位角；当两个角都在两条直线之间，并且分别在截线的两侧，这样的一对角叫作内错角；当两个角都在两条直线之间，并且在截线的同侧，这样的一对角叫作同旁内角．

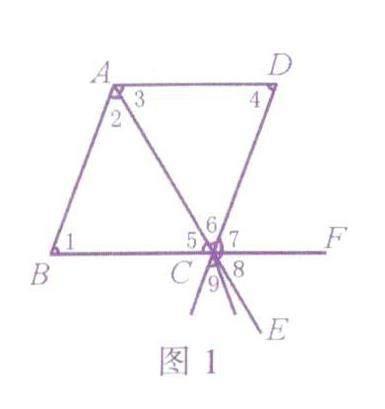
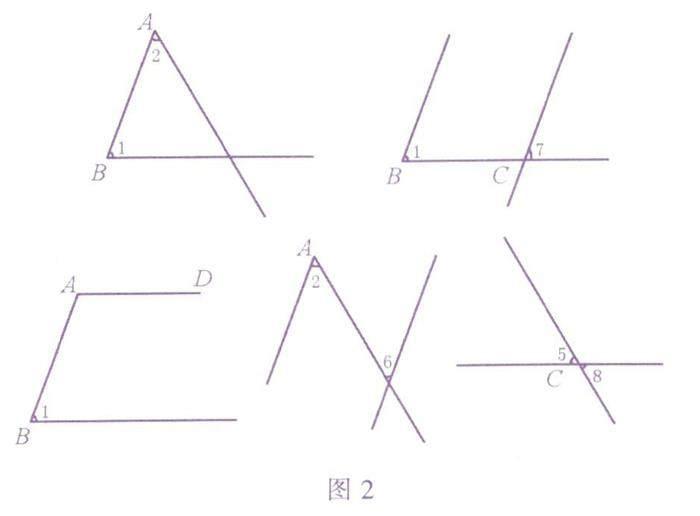
例如，在图1中，判断下列各对角的位置关系：（1）∠1与∠2；（2）∠11与∠7；（3）∠1与∠BAD；（4） ∠2与∠6；（5）∠5与∠8．我们将各对角从图1中“抽”出来，得到图2．

由图2，不难看：∠1与∠2是同旁内角．∠1与∠7是同位角，∠1与∠BAD是同旁内角，∠2与∠6是内错角，∠5与∠8是对顶角．

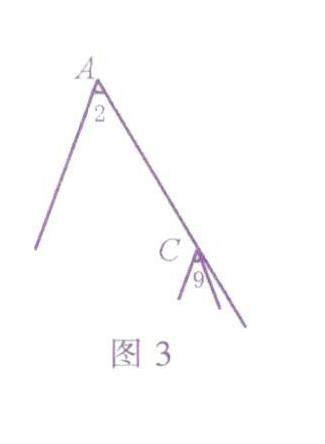
试问：图1中，∠2与∠9是同位角吗？将这对角从图1中“抽”出来，得到图3．由图3可知，∠2与∠9的各边分别在四条不同的直线上，不是两条直线被第三条直线所截形成的，故不是同位角.

平行线及平行公理.在同一平面内， 不重合且不相交的两条直线叫作平行线.

平行公理：经过直线外一点，有且只有一条 直线与这条直线平行.其推论是：如果两条 直线都与第三条直线平行，那么这两条直 线也互相平行.

5.平行线的判定与性质.判定被第三条 直线所截的两条直线是否平行时，要根据图 形，观察所形成的各角中，同位角是否相 等，内错角是否相等，同旁内角是否互补.如 果有满足平行线判定方法中的任何一个所 应具备的条件，就能确定这两条直线互相 平行.平行线的性质：两条平行线被第三 条直线所截，同位角相等（或内错角相等或 同旁内角互补）.简单说成：两直线平行，同 位角相等（或内错角相等或同旁内角互补）.

6.平移.（1）平移只改变图形位置，不改 变图形的形状和大小；（2）新图形中的每一 点，都是由原图形中的某一点移动后得到 的，这两个点是对应点，连接各组对应点的 线段平行（或在同一条直线上）且相等.