“对称性”在高中物理试题解题中的运用例析

俞如新

【摘要】对称是日常生活中随处可见的现象，物理学科同样存在对称现象.在高中物理中，对称性能够在力学中体现，可以在电磁场中应用，同样可以在电学中表现.本文通过具体例题阐述对称性分别在电场、磁场、电路中的表现和应用，帮助学生更深刻地了解高中物理中蕴含的对称性.

【关键词】高中物理；对称性；解题技巧

1 电场的对称性

电场中对称性体现在点电荷周围可见的电场分布具有对称性，利用电场的对称性可以解答点电荷的分布问题、电场强度的叠加问题、电势能问题等.灵活应用对称性，能达到简化问题的目的，从而使问题得到解决.

例1 如图1所示，在竖直平面内固定半径为R的绝缘圆环，有两个可视为点电荷的相同的带负电的小球A和B套在圆环上，其中小球A可沿圆环无摩擦地滑动，小球B固定在圆环上和圆心O的连线与水平方向的夹角为45°，现将小球A由静止释放，则下列说法中正确的有（  ）

（A）小球A运动到圆环最低点Q的过程中电势能先增大后减小.

（B）小球A速度最大处位于Q点的左端.

（C）小球A恰好可以运动到P点.

（D）小球A运动到圆环最低点Q时速度大小为2gR.

解析 当小球A，B均带负电，则根据点电荷的特点可知，当A，B距离缩短时，电场力做负功，电势能增大，反之减小，由图1可知，小球A运动到圆环最低点Q点过程中，与B电荷距离先增大后减小，则电势能先减小后增大，故（A）错误.

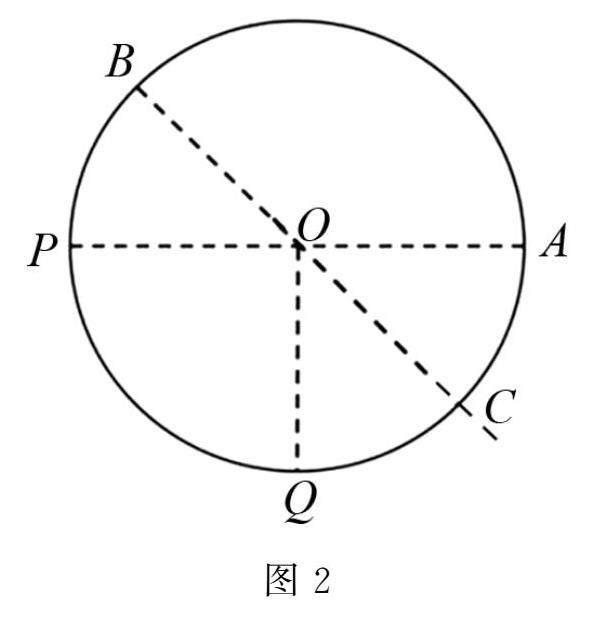
延长BO与圆周交于C点，如图2所示，小球在下降过程中，当小球A，B距离增大时，即AC段，电场力做正功，重力做正功，速度增大；CQ段，小球A，B距离减小，电场力做负功，重力做正功；PQ段，小球A，B距离减小，电场力做负功，重力做负功，小球速度减小，可知小球速度最大处不位于Q点左边，故（B）错误.

小球在A，P两点相比，重力势能相同，但P点与B球距离更小，则A到P过程电场力做负功，电势能增大，则需要有外力做功才能达到P点，故（C）错误.

由图1可知，A，Q两点与小球B距离相同，则电势能相等，在A到Q过程中动能增加量等于重力势能减少量，可得12mv2Q=mgR，解得vQ=2gR.故选项（D）正确.

2 磁场的对称性

对称性在磁场中有三方面的体现，即直线电流磁场具有对称性、通电螺线管磁场具有对称性、带电粒子在有界磁场中进行对称运动.运用磁场对称性解题，同样能让问题得到简化，使问题更加有效地被解决.

例2 已知直导线中电流在周围空间产生的磁感应强度大小为B=kIr，k为常量，I为电流强度，r为导线的距离.b，c，d三根长通电直导线垂直于纸面放置，电流方向如图3所示，ac垂直于bd且ab=ad=ac，b，c，d三根导线中电流强度分别是I，I，2I.已知导线c在a点的磁感应强度大小为B，则a点处的合磁感应强度大小为（  ）

（A）10B.   （B）3B.

（C）22B.  （D）7B.

思考 在合磁场求解问题中，应注意b，d导线在a处产生的磁场是对称的，故需要根据大小来考虑磁场的方向，其次磁场应根据平行四边形法则求解，得到最终值.

解析  由于直导线c在a点处的磁感应强度大小为B，又因为b，c，d三根导线中电流强度分别为I，I，2I，且ab=ad=ac，所以直导线d在a點的磁感应强度大小等于2B，根据安培定则可判断磁场方向如图4所示.

b和d直导线在a点的磁感应强度方向向左，合成后大小为3B，c直导线在a点产生的磁感应强度方向向下，大小为B，根据平行四边形法则，可知a点磁感应强度大小为B合=3B2+B2=10B，故正确答案为（A）.

3 电路的对称性

利用电路的对称性可以对较为复杂的电路进行简化，得到更为直观的等效电路，从而使问题得到解决.

例3 图5所示为一个立方体ABCDEFGH，每边都用导体接入一个电阻值为r的电阻，试计算A，G点间的等效电阻RAG.

解析 由于对称性，设端点A流入电流I，分流后最后在G点汇合流出，B，D，E三点为等势点，故可用导线连接而不会改变线路的电流，对C，H，F三点来说，情况也是这样，故可得等效电路，如图6所示.

图6中各电阻阻值均为r，所以A，G之间的总电阻为RAG=r3+r6+r3=5r6.

4 结语

通过以上的例证和分析，我们可以看出“对称性”在高中物理试题解答中的重要作用，特别是在处理电场、电路和磁场相关问题时.正确识别和运用对称性可以有效简化问题，减少计算量，进而提高解题效率.然而，需要注意的是，识别对称性并不总是简单的，需要学生具备扎实的物理知识和逻辑思考能力.期望学生在今后的学习中能够持续深入理解对称性的概念，提高在解题中对其进行运用的技巧，从而在物理试题解答中获得更好的成绩.

参考文献：

[1]唐在山.例谈“对称法”在高中物理解题中的应用[J].湖南中学物理，2017（06）：96-98.