两维异质性面板分位数模型的双惩罚回归方法

任燕燕，李东霖，王文悦

（山东大学 经济学院，济南 250100）

0 引言

在现代经济问题实证研究中应用的样本数据逐渐呈现大数据特征，由于数据来源具有多样性、复杂性，经济大数据集表现出显著的异质性特点，原有基于同质性假设的单一化等传统建模方法无法全面揭示经济运行的客观规律。因此，异质性分析是计量经济学和统计学中的一个研究热点，如何处理经济大数据中的异质性并分析经济变量之间的结构关系或变化是该研究的关键所在。利用面板数据模型进行异质性分析的研究大多基于均值回归假设进行，回归结果只能刻画均值水平上的异质性结构，未能全面考虑数据所蕴含的信息。而基于面板分位数模型的异质性分析方法能够从被解释变量条件分布的角度，更加全面地反映不同分位点处变量之间的回归关系，并识别其异质性结构。其中，一部分学者基于个体维度的异质性，研究组群结构的识别方法。Zhang 等（2019）[1]考虑个体维度上的组群结构，提出了面板分位数模型的聚类方法，并借鉴机器学习中的K-means 算法开发了用于识别某一分位点处或不同分位点间组群结构的迭代算法；Zhang 等（2023）[2]提出了一种关于面板分位数模型组群结构的非参数估计方法，使用两两融合的惩罚项估计了组群结构的数量，通过ADMM 迭代算法提高了运算效率。另外一部分学者关注时间维度上的异质性，试图寻找未知的结构变点。Wang 等（2009）[3]基于回归系数是关于时间的平滑非参数函数的假设，构建了变系数分位数回归模型，并且使用基函数近似法进行参数估计；部分学者提出了具有结构变点的分位数自回归模型，根据非对称Laplace 分布构建似然函数，实现了对结构变点的估计；Lee等（2018）[4]构建了具有结构变点的分位数回归模型，利用L1惩罚项结合加权绝对偏差项构建目标函数，估计了该模型的回归系数和结构变点，同时证明了估计量具有Oracle属性。上述针对异质性面板分位数模型的研究，普遍基于个体或时间的单一维度进行分析，然而随着异质性分析方法的不断发展，一些实证研究结果表明，变量之间的关系可能同时存在个体和时间两个维度上的异质性，因此有必要假设模型存在两维的异质性结构。

两维异质性面板分位数模型存在严重的冗余参数问题，因此减少待估参数的数量成为相关研究的关键。一种方法是将两维异质性系数分解为个体维度的异质性系数、时间维度的异质性系数和共同系数三项之和，称为维数缩减法[5]。此类方法存在模型识别问题，系数分解需要满足个体和时间维度的异质性系数均值为零的假设，重点考察通过系数分解得到的共同系数。另一种方法假设系数在个体和时间两个维度上存在异质性结构，根据不同问题的研究背景，设定两维异质性系数具有不同的稀疏结构，基于某一维度的异质性结构关注另一个维度上是否存在组群结构或结构变点。Okui 和Wang（2021）[6]在基于个体维度识别出组群结构的基础上，考察不同组群时间维度上的结构变点，提出利用Adaptive Lasso进行组群融合的方法；Lumsdaine 等（2020）[7]关注面板数据模型在时间维度上的某一结构变点，基于K-means算法识别该结构变点附近个体维度上的组群结构是否发生变化。此外，部分研究假设模型系数在个体或时间中某一个维度上存在稀疏结构，而在另一个维度上存在完全异质性。Baltagi等（2016）[8]允许不同个体的斜率系数存在差异，但斜率系数具有相同的结构变点；Su 等（2017）[9]假定不同个体之间存在组群结构，并且具有时间维度上的时变非参数形式的异质性系数，利用筛法或B-样条将个体维度和时间维度进行分离，考虑分离出的个体维度并识别其组群结构。迄今为止，尚未有文献研究面板分位数模型的两维异质性问题。本文考虑系数具有两维异质性结构的面板分位数模型，基于SCAD惩罚函数和MCP惩罚函数提出一种能够同时进行参数估计和两维异质性结构识别的双惩罚回归方法。

1 模型设定和估计方法

1.1 两维异质性面板分位数模型

本文考虑如下的两维异质性面板数据模型：

其中，yit表示一维被解释变量，μit表示随个体和时间同时变化的固定效应项，zit=(zit,1,zit,2,…,zit,P-1)Τ表示P-1 维 解 释 变 量 向 量，δit=(δit,1,δit,2,…,δit,P-1)Τ表 示P-1 维异质性解释变量系数，εit表示一维随机误差项。定义和。在分位点τ处，可构建如下的条件分位数函数：

模型存在冗余参数问题，为了减少待估参数，本文假设斜率系数βit(τ)具有如下的两维异质性结构：

其中，B(τ)={B1(τ),B2(τ),…,BL(τ)(τ)}表示两维异质性结构，L(τ)表示其数量。

1.2 双惩罚最小加权绝对偏差目标函数

其中：ρτ(u)=u∙(τ-I(u<0))表示分段线性分位数损失函数；I(∙)表示示性函数，当括号内不等式成立时取值为1，否则取值为0。因此ρτ(u)的分段函数为：

pλ(τ)(∙)和pγ(τ)(∙)表示成对融合惩罚函数，分别基于个体维度和时间维度对两维异质性结构进行融合，λ(τ)和γ(τ)表示控制惩罚力度的调节参数。常用的Lasso惩罚函数pλ(t)=λt对所有的或使用相同的阈值，因此过度收缩了较大的模型参数，导致估计量存在偏差并且可能无法正确识别模型的异质性结构。因此，本文使用能够产生无偏估计的惩罚函数，包括Fan和Li（2001）[10]提出的SCAD惩罚函数：

Zhang（2010）[11]提出的MCP惩罚函数：

其中：(∙)+=max(0,∙)；a表示控制惩罚函数凹性的参数，在本文中视作一个固定常数；t表示基于个体维度或时间维度模型参数的差异，即‖βit(τ)-βjt(τ) ‖或‖βit(τ)-βit′(τ) ‖。SCAD 惩罚函数和MCP 惩罚函数均为渐进无偏的，能够更加精确地识别模型参数的异质性结构。特别地，当a→+∞时，SCAD惩罚函数和MCP惩罚函数收敛到Lasso惩罚函数。

对于给定的λ(τ)和γ(τ)，参数估计量可通过最小化目标函数给出：

1.3 参数估计的ADMM算法

考虑到最小化目标函数S(β(τ);γ(τ),λ(τ))这一无约束优化问题的显式解不存在，本文拟使用求解优化问题的交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）估计分位点τ处的斜率系数β(τ)。基于目标函数S(β(τ);γ(τ),λ(τ))，考虑如下约束条件：

其中，ηij,t(τ)表示在分位点τ处和相同的时间点t不同个体i和j之间斜率系数的差异，θi,tt′(τ)表示在分位点τ处同一个体i在不同时间点t和t′之间斜率系数的差异。因此，可以将原有的无约束优化问题转化成有约束的优化问题：

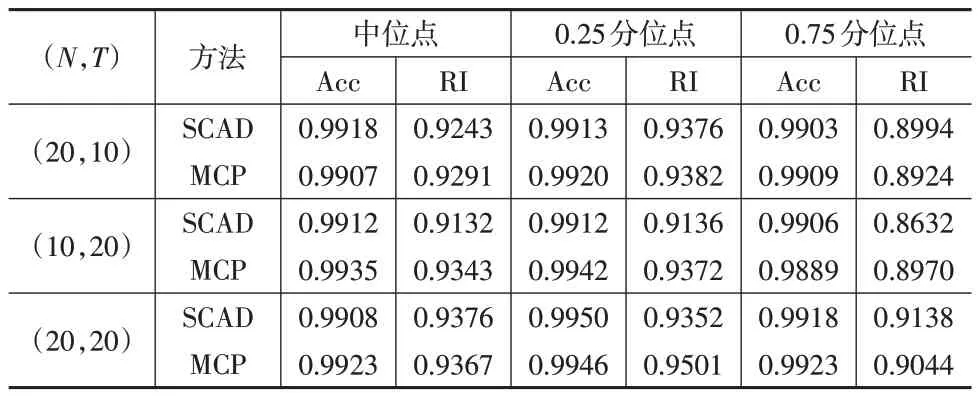
其中，η(τ)=(t(τ),i

本文使用ADMM 算法，从给定的初始值开始逐步更新β(τ)、η(τ)、θ(τ)、v(τ)和w(τ)的迭代值。假设第s步的迭代值β(s)(τ)、v(s)(τ)和w(s)(τ)是已知的，第s+1 步使用ADMM 算 法 获 得 迭 代 值β(s+1)(τ) 、η(s+1)(τ) 、θ(s+1)(τ) 、v(s+1)(τ)和w(s+1)(τ)的具体步骤为：（1）根据β(s)(τ)、v(s)(τ)和w(s)(τ)，更新迭代值η(s+1)(τ)和θ(s+1)(τ)；（2）根据v(s)(τ)和w(s)(τ)以及第一步迭代得到的η(s+1)(τ)和θ(s+1)(τ)，更新斜率系数的迭代值β(s+1)(τ)；（3）根据相关参数，更新迭代值v(s+1)(τ)和w(s+1)(τ)。基于以上步骤，更新迭代值的详细过程为：

首先，更新迭代值η(s+1)(τ)和θ(s+1)(τ)的子优化问题为：

使用不同的惩罚函数，即使在目标函数不可导的情况下，依然能使用凸分析中的次微分得到和的迭代公式。

如果参数满足a>max(1/φ+1,1/ϕ+1)并且使用SCAD惩罚函数，那么迭代公式为：

其中，ST(z,t)=(1-t/‖ω‖ )+ω表示软阈值算子（Soft Thresholding Operator），并且(∙)+=max(0,∙)。

如果参数满足a>max(1/φ,1/ϕ)并且使用MCP惩罚函数，那么迭代公式为：

其次，模型斜率系数的迭代值β(s+1)(τ)可以通过如下无约束最优化问题计算：

其中，η(s+1)(τ)、θ(s+1)(τ)、v(s)(τ)和w(s)(τ)均已知。目标函数等价于：

最后，使用对偶上升法（Dual Ascent）计算对偶变量v(τ)和w(τ)的迭代值，迭代方向取增广拉格朗日目标函数L对对偶变量的次微分，迭代步长选择固定的惩罚参数φ和ϕ。因此，(τ)和(τ)的计算公式为：

2 蒙特卡洛模拟

2.1 数据生成过程

本文使用蒙特卡洛模拟验证提出的基于双惩罚最小加权绝对偏差目标函数系数估计量的有限样本性质。每轮蒙特卡洛模拟使用的数据{yit,xit}（i=1,…,N；t=1,…,T）基于如式（26）所示的数据生成过程得到。不失一般性，考虑二变量面板数据模型：

其中，N=10,20，T=10,20，固定效应项μit和解释变量系数ηit具有相同的两维异质性结构。假设两维异质性结构的数量为L=2，并且每一个两维异质性结构系数的真实值为α1=(-2,3)和α2=(3,5)。具体两维异质性结构 可 任 意 设 定，例 如N=20 和T=20 ，当6 ≤i≤8 且8 ≤t≤12，以及9 ≤i≤13 且6 ≤t≤15 时，(i,t)属于两维异质性结构B2；否则，(i,t)属于两维异质性结构B1。B1和B2元素数量的比例 |B1|:|B2|≈5:1。假设xit的生成过程满足：

2.2 蒙特卡洛模拟结果

本文在蒙特卡洛模拟的过程中选择重复次数n=200 。调节参数λ和γ的网格搜索筛选范围为[0.1,1.9]，搜索步长为0.2。为了验证估计量的有限样本性质，本文将基于SCAD 惩罚函数和MCP 惩罚函数的估计结果与Post 估计量（见式（28））和Oracle 估计量（见式（29））进行比较。

其中，B̂表示两维异质性结构的估计值，L̂表示两维异质性结构数量的估计值，B0表示两维异质性结构的真实值，L0表示两维异质性结构数量的真实值。根据参数α的估计量和相应的两维异质性结构，能够得到参数β的Post估计量和Oracle估计量。

为了评估模型参数估计结果的精确度，下页表1和表2分别汇报了基于同方差假设和异方差假设的中位点处、0.25 分位点处和0.75 分位点处系数估计值的均方误差和平均偏差。结果显示，在各分位点处，本文提出的应用SCAD 惩罚函数和MCP 惩罚函数的参数估计方法的估计结果相似，并且Post 估计量的RMSE 与Bias 和Oracle 估计量差别不大。

表1 同方差假设下参数估计的RMSE和Bias

表2 异方差假设下参数估计的RMSE和Bias

为了检验本文提出的两维异质性结构识别方法的准确性，下页表3和表4分别汇报了同方差假设下和异方差假设下不同分位点处两维异质性结构估计的准确率和Rand 指数。结果表明，本文提出的方法在所有情况下都能准确地识别各分位点处的两维异质性结构，而且基于SCAD 惩罚函数和MCP 惩罚函数的估计方法在两维异质性结构识别方面的表现相近。

表3 同方差假设下两维异质性结构估计的Acc和RI

表4 异方差假设下两维异质性结构估计的Acc和RI

3 应用

本文将提出的双惩罚最小加权绝对偏差估计方法应用于2009—2019 年我国31 个省份（不含港澳台）的GDP数据，以识别不同省份和不同年份经济发展的两维异质性结构并进行参数估计，研究使用的数据来源于国家统计局官网。考虑如下两维异质性面板分位数模型：

其中，l n(GDPit)表示省份i第t年人均GDP的自然对数值，t=0 对应于2009 年，βit(τ)=(βit,0(τ),βit,1(τ),βit,2(τ))Τ表示具有未知两维异质性结构的异质性斜率系数，(i,t)∊Bl，{B1,B2,…,BL}表示未知的两维异质性结构，εit(τ)表示随机误差项。调节参数λ(τ)和γ(τ)的选择范围为[0.1，1.9]，步长为0.2，考虑τ=0.25，τ=0.5 和τ=0.75 三个分位点。应用本文方法估计上述模型，估计结果表明，各分位点处的两维异质性结构数量L̂(τ)均为2。

表5列出了模型的参数估计结果，发现各分位点处识别出不同两维异质性结构的参数存在显著差异。首先，不同两维异质性结构的截距项在各分位点处均存在显著差异；其次，GDP 一阶滞后项的系数即自回归系数在不同两维异质性结构下和不同分位点处均显著但差距较小；最后，各分位点处不同两维异质性结构之间时间斜率系数的差异主要体现在其显著性上，其中一个两维异质性结构时间的斜率系数显著，而另一个两维异质性结构的系数不显著。上述结果表明，我国各省份在研究期间的经济发展状况存在两维异质性，本文提出的方法实现了对两维异质性结构的估计。

表5 各分位点处不同两维异质性结构的参数估计结果

4 结论

本文研究了具有两维异质性结构的面板分位数模型及其参数估计问题。利用SCAD 惩罚函数和MCP 惩罚函数在个体维度和时间维度上对异质性参数进行融合，构建了双惩罚最小加权绝对偏差目标函数，并通过设计ADMM迭代算法求解该目标函数，实现了参数估计和两维异质性结构识别。根据蒙特卡洛模拟验证了双惩罚估计量的有限样本性质，无论基于同方差假设还是异方差假设，本文提出的方法均能准确地识别各分位点处的两维异质性结构，并且Post估计量的RMSE和Bias接近于假设真实两维异质性结构已知的Oracle估计量。进一步地，将本文方法应用于中国省级GDP回归的估计，估计结果表明，我国各省份在研究期间的经济增长存在两维异质性，本文提出的方法能够识别这种两维异质性结构。