科研项目和员工绩效综合评价方法研究

林从龙

［摘 要］本文通过数据的统计分析，应用正态分布曲线与项目检查评估分数分布曲线关系，将项目检查评估分数进行分段量化，使项目考核更具依据性，并将项目检查评估分数的历史数据考虑进来，使项目考核更加公平、合理。以此方法为基础，类推将企业各项考核打分机制构成一个系统，在数据层面进行统一，构建企业、员工考核评估大平台，使考核公开、公平化。让每一个员工在以数据为基础的量化、公开平台上，受到真正的激励，减少在各项激励过程中的人为因素，让激励取得更好的效果。

［关键词］正态分布；科研管理；人才绩效；科研项目评估；数据统计分析

doi：10.3969/j.issn.1673-0194.2024.05.041

［中图分类号］F272.92 ［文献标识码］A ［文章编号］1673-0194（2024）05-0137-04

0     引 言

以科技项目研究为主体的研究单位，在项目检查过程中，为激励科研人员的科研热情，考核项目研究进展及成果，普遍采取打分制，对各类项目研究进展、研究成果完成情况进行专家评比打分。专家评分制度为的是综合各方面专家的能力，在项目评价过程中，确保项目检查评价的公平性，通过专家评分，激励科研人员。但在实际执行过程中，取得的激励效果甚微，没有取得预期的实际应用效果，其主要原因为各项评估数据出来后，仅以会议纪要等形式公布，未真正地找到很好的方法将这些数据与员工考核评估相联系，且各项目的分数基本在“优秀分”（大于80分）以上，打分数据无法从直接分数上准确体现项目开展情况好坏，难以从分数上给项目经理以正向激励。久而久之，项目组便形成了对评估分数的不敏感、不重视、不关注。从而，失去了项目检查评估的激励和督促意义，反而让部分项目经理自我感觉良好。为更好地评估项目运行情况，必须形成一套完整的数据分析方法，将项目检查评估分数数据有效地利用起来，真正起到激励、督促项目组积极开展科研的作用。

1     基本理论

1.1   正态分布理论

正态分布（Normal distribution）又名高斯分布（Gaussian distribution），是一个在数学、物理及工程等领域都非常重要的概率分布［1］。正态分布是具有两个参数μ和δ2的连续型随机变量的分布，参数μ是遵从正态分布的随机变量的均值，参数δ2是此随机变量的方差，所以正态分布记作N（ μ，δ2）［2-4］。当μ=0，δ2=1时，称为标准正态分布，记为N（0，1）。

1.2   中心极限定理

由中心极限定理可知，如果一个量是由许多微小的独立随机因素影响的结果，那么就可以认为这个变量的分布近似地趋于正态分布［5-6］。中心极限定理（Central Limit Theorem）是概率论的重要内容，也是数理统计学的基石之一［7］。根据不同的假设条件，中心极限定理有多个，独立同分布中心极限定理和棣莫弗－拉普拉斯中心极限定理最为常用，其中棣莫弗－拉普拉斯中心极限定理［8］如下：

设随机变量ηn（n=1，2，…）服从参数为n，p（0＜p＜1）的二項分布，则对于任意x，有

该定理表明，正态分布也可认为是二项分布的极限分布。当样本量n逐渐增大时（通常要求n≥30），无论总体分布如何，样本均值的概率分布都将近似服从正态分布，且其分布的期望值等于总体均值μ，方差等于总体方差的1/n，这就是统计学上著名的中心极限定理，可以表述为：从均值为μ、方差为δ2的总体样本中，抽取样本量为n的随机样本，当n充分大时（一般情况下n≥30），样本均值的分布近似服从均值为μ、方差为δ2/n的正态分布，即，

等价地有［9］。

2     数据分析

2.1   数据处理

科研单位拥有完整的科技项目管理制度，依据科技项目管理制度，对科技项目进行检查，一般采取专家打分的方式进行，历史同类项目的执行流程具有可聚类性和可对比性。科技项目检查专家打分结果，根据中心极限定理，为许多微小的独立随机因素影响的结果，其数据符合正态分布。可利用正态分布的偏度系数和峰度系数，对数据符合正态分布进行论证，在本文中将不对此进行叙述。

本文以科研单位科技项目检查专家打分数据为基础，运用正态分布曲线拟合的方法对其分析研究。根据科研项目检查打分数据，按照各分值出现的频率，进行数据分析。数据体最小值为55，最大值为99，并对数据体按照单个数据出现频率分布进行了统计，除以数据体总数，得出每一个数据出现频率的概率，以此打分数值和数值出现的频率，作为正态分布拟合的数据基础。

2.2   数据拟合

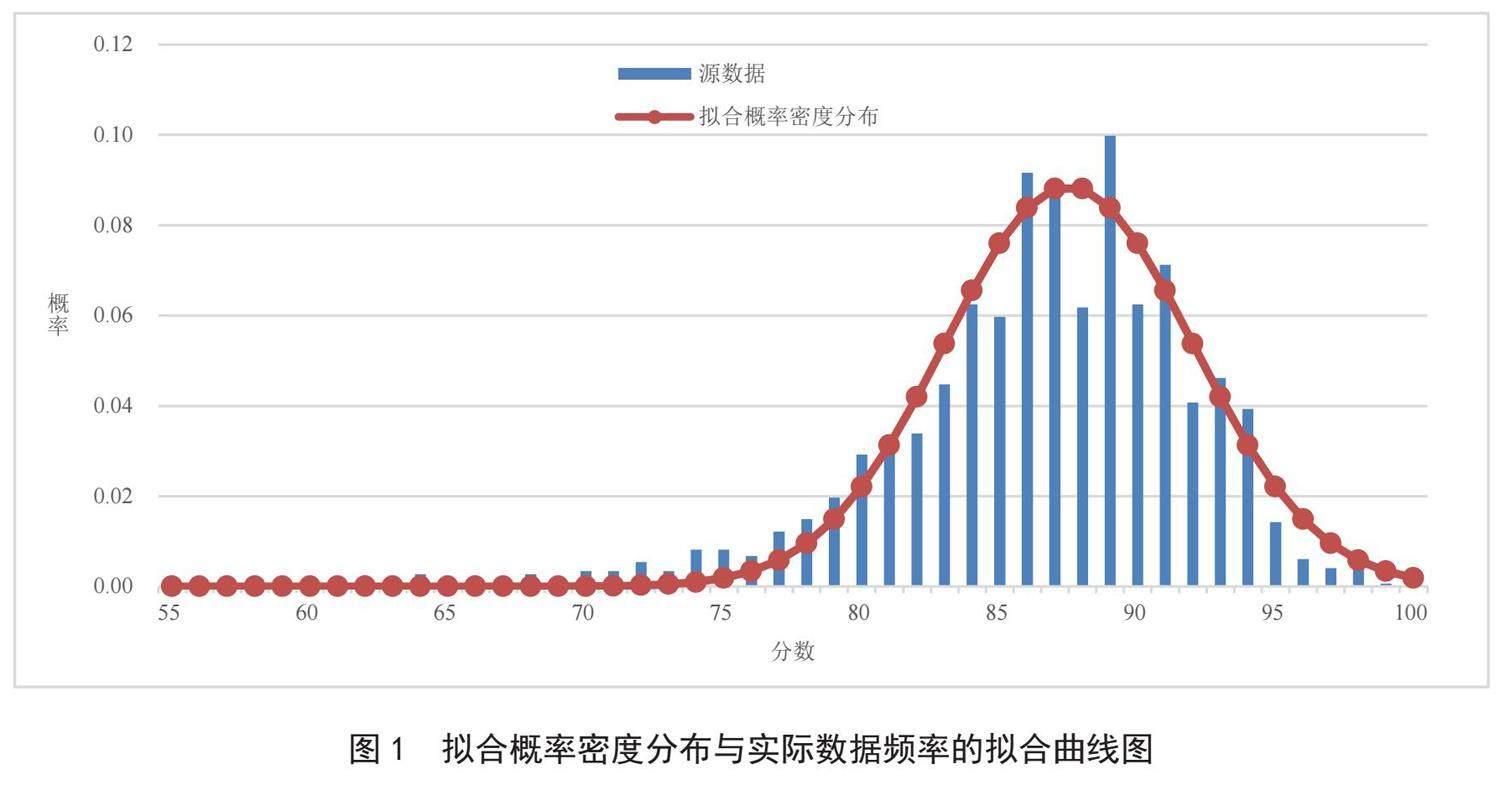
计算数据体平均值和方差，根据正态分布概率密度函数，计算55到99这个数据段数据的概率，然后通过改变正态分布中的μ和δ2，将正态分布曲线与原数据曲线进行拟合，本次数据拟合度为0.9414，从概率统计角度来说，精准度达到94%，拟合曲线如图1所示。根据大数定律和中心极限定理，随着数据体的增大，其数据分布会更加接近和符合正态分布［10］。

2.3   拟合概率密度函数解析

如表1所示，以拟合正态分布曲线数据为基础，根据拟合的正态分布曲线性质及正态分布概率密度函数公式可以计算各数据段的概率。同时，在已知一个项目的检查评估分数时，可以根据拟合的概率密度分布函数，计算出处于历史项目检查评估数据中的位置。例如：数据段80到90分之间的概率公式为

=90.44%，也就是在已知数据体中，80到90分数段的出现概率为90.44%。如果已知一个科研项目检查分数为89分，可以知道这个分数只是处于已知数据体中的前36.94%。如果科研项目评比分数前10%评定为优秀项目，要达到前10%，检查分数必须达到93.26分。根据源数据与拟合曲线数据特征值分析，两者具有相近性，同时验证了以拟合曲线函数去预测项目检查评估数据所处的数据段是可行的。

美国通用电器公司为激励员工，认为最优的员工评价分段比例为后10%、中间70%、前20%［11］。根据拟合正态曲线可以对企业项目检查评估分数进行量化分段评估，可得出各分段检查评估分数分布，根据历史数据分析，分数段在后10%分数处于0分到82分之间，占比中间70%的分数处于82分到91分之间，占比前20%高分段在91分到100分之间，如图2所示。

如果将评分分为三段，前20%为优秀，中间70%为良好，后10%为一般。由历史数据分析可知，即使某些科研项目检查得分为80分以上，但并不意味着此项目运行情况在整体的项目评分中是良好或优秀，而可能它处于历史项目检查评估分数中的后10%，在企业历年项目检查评估分数中，处于完全落后状态，这种项目作为管理人员应该予以重点关注；如果科研项目检查评估要进入前20%，达到优秀水平的话，根据以往历史数据，其项目检查评估分数要达到91分以上。

3     数据应用

实际应用时，数据体可根据每年项目检查评估分数进行更新，得出更优的拟合的曲线；反过来也可以利用拟合的正态分布曲线，用以检验科研项目检查打分的公平性、诚实性。当应用此方法得出的数据与奖励、岗位晋升结合时，不仅能最大程度将奖惩公开化，体现公平、公正性，而且能确保工作成效好的员工真正得到奖励，使员工奖励、晋升让人信服，从更加统一的数据平台层面上激励员工工作热情，树立令人信服的典型。提高领导公信力、企业公信力，真正意义上达到团结员工、凝聚力量、激励科研人员的效果。

同时，可以将此方法应用到人力资源考核体系等其他数据体，从多个方面数据入手，进行同层次整合统一，划分出前20%员工给予岗位晋升方面、培训方面、薪酬方面的奖励，划分出中间段70%中最具潜力的人给予重点培养，建立一套完善的绩效考核流程，有利于提升考核工作公开、公平、公正的水平，促使形成一个团结、竞争、积极的企业，极大地增强企业的文化实力和战斗力，对储备管理、技术人才，意义重大而深远。

4     结 论

本文从概率统计的角度，应用项目检查评估分数与正态分布很好的相关性，对项目检查评估分数进行了统计分析，提出了企业范围内各项打分制度的数据分析方法，给出了具体分析流程，也从实际数据体的拟合方面反向论证了项目檢查评估分数符合正态分布这一特点。

利用此方法不仅可以优化现有的科研项目评估制度，而且能利用此方法，结合各数据体拟合曲线特征，设置权重，将所有数据放在统一平台，对企业员工工作表现情况和潜力予以评估，给出奖励及重点培训对象建议，有效避免人才选拔过程中的人为干预，用数据说话，有效避免人员使用时亲疏有别的现象，促进企业各项信息的公开化，将企业奖励制度发挥到最大效果，树立真正意义上的典型。

主要参考文献

［1］盛骤，谢式千，潘承毅.概率论与数理统计［M］. 4版.北京：高等教育出版社，2008.

［2］王红军，田铮，武新乾.二元正态混合模型的偏度与峰度［J］.系统仿真学报，2008（4）：855-857，861.

［3］刘剑波.基于多元混合正态分布的期权组合VaR度量研

究［D］.杭州：浙江财经学院，2010.

［4］陈晓林，汪四水.一类混合正态分布参数估计的EM算法和数据扩张［J］.苏州大学学报（自然科学版），2007（3）：13-17，54.

［5］王维，向瀚淋，龚雯丽，等.常见分布中心极限定理适用样本量研究［J］.高师理科学刊，2021，41（7）：20-25.

［6］王伟珠.论中心极限定理及应用［J］赤峰学院学报（自然科学版），2013（19）：1-2.

［7］秦信念，沈林.中心极限定理在社会生活和军事问题中的应用［J］.旅游纵览（下半月），2013（16）：296.

［8］杨桂元.中心极限定理及其在统计分析中的应用［J］.统计与信息论坛，2000（3）：13-15.

［9］王典妮，刘修生.中心极限定理及其应用［J］.湖北理工学院学报，2018，34（5）：57-62.

［10］张志成，张艳.中心极限定理在实际中的应用［J］.河南工学院学报，2020，28（4）：28-30.

［11］李广平.基于价值观的人力资源管理：GE人力资源管理体系剖析［D］.郑州：郑州大学，2004.