高中数学教学设计

史娜

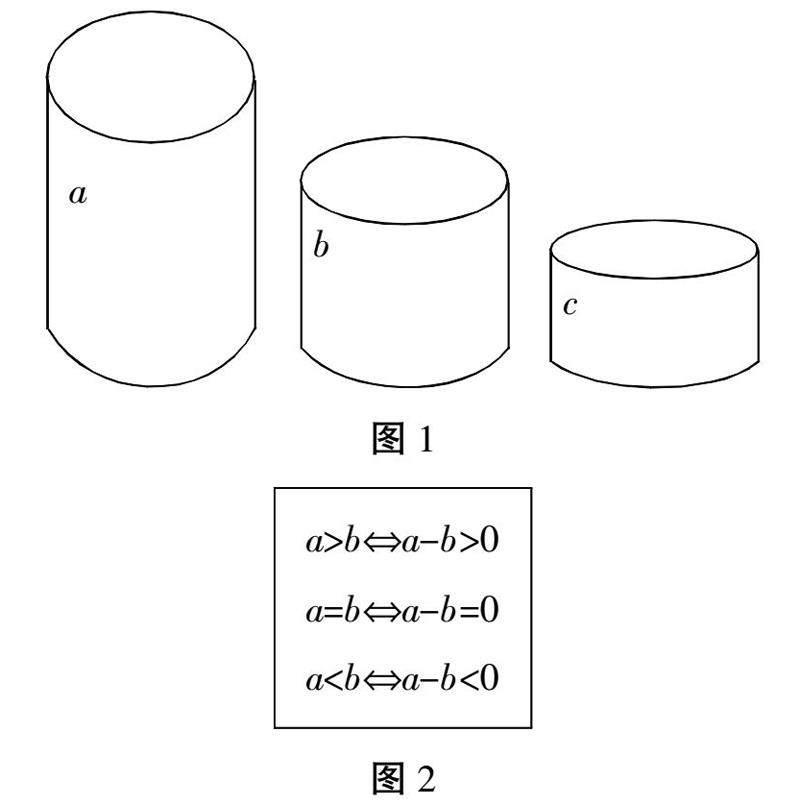
在高中数学教学中，不等式的性质部分是十分基础又十分重要的内容。但传统的教学模式达不到理想的教学效果，反而会影响学生的学习欲望，让学生在面对越来越复杂、越来越难的数学知识时望而却步。因此在教学中，教师要贯彻以生为本的理念，从学生的认知规律角度出发，以学生更易于接受、乐于接受的形式展开教学。

一、教学内容和目标

不等式的性质是高中数学中的重点和难点部分，其本质是式与式之间的数量关系，也是实数序关系的一般化表现。实数的大小关系往往是客观的现实，无法更改，这也是不等式性质的基本逻辑。虽然等式和不等式都是“式”，但不等式具有明显的方向性，在运算过程中更是如此。学生只有掌握不等式的基本性质，才能为后续的数学学习打下良好基础。

教学目标：

1.回顾等式的基本性质，运用类比的方式推理出不等式的性质。

2.合理运用不等式的性质知识点，以及作差比较法、函数图象等方式来证明不等式。

3.在不等式的性质知识中，通过推理、猜想、证明等方式，锻炼学生的逻辑推理能力。

4.掌握不等式的基本研究思路与方法。

5.通过该章节知识点的学习，将实际问题转变为数学问题，培养学生的数学思维能力。

二、教学实施

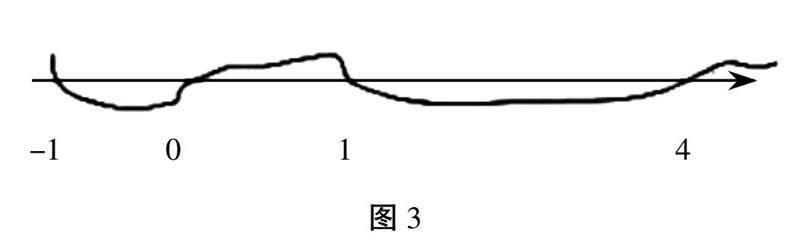
（一）课题导入

虽然高中生在数学方面已经有了较为稳固的学习基础，但也要采用相对灵活、有趣的方法来导入新课，本次教学利用了一个简单有趣的实物展示引起话题，之后引导学生根据事物内在联系推导出不等式的概念和性质，从简单的概念入手，以更加具象化的方式将不等关系表达出来。如图1所示，先为学生展示三个大小个不相等的圆柱体，并让学生说一说这三个圆柱体的大小关系是怎样的。学生经过观察能够快速答出a>b>c的结论，其实这一结果就能体现不等式的传递性。之后让学生根据图片进行总结，分别说出其大小关系，如a>b、b>c、a>c、c

（二）化繁为简，理清知识概念

进入高中阶段以后，很多学生会发现一个问题，随着知识学习程度的加深，往往会接触到越来越多的数学概念名词。这些名词是数学现象的一种总结，但有时候也会让学生将原本理解的知识或现象变得复杂起来，给学习造成障碍。而作为教师，我们需要让学生的这种学习压力最小化，尽量采用生活化的语言将知识化繁为简。在“不等式的性质”的教学中，教师需要将数学符号语言转变为学生易于理解的形式，通过生活化的表达降低理解难度，并让学生在理解知识点时找到认知基础。在“不等式的性质”的学习中，学生会接触到很多类似a>b、a+b>c、ab>b+c的式子。对此，在教学中，我们可以用通俗易懂的方式引导学生。之后就可以代入到不等式的性质1，运用符号语言和文字语言两种方式阐述，在比较两个不同且不为0的数时，一般通过大于或小于两种关系进行表示，要么这个数大于那个数，要么这个数小于那个数，这两种说法表达的意思相同，转换为符号语言即为如果a>b，则bb。在引入这一概念时，教师需要帮助学生理清前后的因果关系以及等效符号“”，这代表符号两边可互推，也就是可以通过等效符号左边的不等式推导出右边的不等式;不等式的性质2：当一个数大于另一个数，另一个数又大于第三个数，根据它们的关系可以得出第一个数大于第三个数，即如果a>b，b>c，则a>c;不等式的性质3：在不等式两边同时加上或减去一个相同的数，不等式符号不会发生改变，即如果a>b，则a+c>b+c;不等式的性质4：在不等式两边同时乘以一个数，若该数大于0则不会改变不等式方向，若该数小于0则改变不等式方向，即如果a>b，c>0，则ac>bc;若c<0则acb，c>d，则a+c>b+d，其涉及了两个数量关系的整合。可以通过表格的方式帮助学生掌握不等式的基本性质，同时和等式的性质进行对比，理解两者之间的共同点和不同点，加深知识印象。

（三）层层递进，构建完整的知识网络

由于不等式的性质中，性质1到性质3可以根据等式的学习经验轻松理解，但性质4和性质5则有所不同，性质4是学习中的难点，所以可以采用层层递进的方式，带领学生根据性质3试着推导出性质4。

方法一：假设a-b的结果。

由于-a=（-1）×a，-b=（-1）×b，因此不等式两边同时乘以一个相同的负数，不等号的方向将会发生改变。通过性质3，在原式中减去相同的（a+b），再将结果化简就能得到一个将不等号两边互换的结果，经过转化顺利推导出性质4。之后让学生试着探索a>b的情况是否能推導性质4，其过程如下：

方法二：假设a>b，根据不等式性质3，在不等号两边同时减去（a+b），可得a-（a+b）>b-（a+b），经过化简可得-b>-a，也就是-a<-b的结果。由于-a=（-1）×a，-b=（-1）×b，所以不等式两边同时乘以一个相同且小于0的数，不等号的方向会发生转变，同样能得到性质4。

（四）新知旧识结合，强化类比思维

新旧知识结合能够让学生巩固旧知识，同时为学习新知识打下基础。与不等式的性质相关的过往知识有很多，如等式、方程等，需要根据学习的进度和内容选择对应的关联知识点。如将不等式部分与学生以往学习过的方程进行结合，并提出问题：类比方程x2-5x=0的根和函数y=x2-5x的图象关系，分析不等式x2-5x≤0的解集。

首先，教师可以引导学生根据题目要求试着画出函数的图象，观察函数图象中的零点和方程x2-5x=0的根有什么关系。零点和两边值的符号应当是什么？可以用这个方法求得不等式x2-5x≤0的解集吗？经过思考和运算，学生能够发现零点是方程的根，也就是0和5，再根据零点的性质能够了解到，0与5两侧的值分别大于0和小于0，所以不等式的解集为{x|0≤x≤5}。将方程知识与不等式结合，引导学生采用类比思维来探索新知识，可以培养学生归纳总结的能力，也可以让学生学会主动探索数学问题，培养对数学知识的学习兴趣。

（五）练习反馈，继续提升

1.假设a>b，请将正确的不等号填入以下圆圈内，并说明解答该题引用了不等式的哪一条性质。

（1）a-3 ○ b+2    （2）-a ○ -b

（3）-3a ○ -3b    （4）a-5 ○ b-5

（5）a/2 ○ b/2     （6）3a+3 ○ 3b+3

2.在下列横线上填上正确的不等号，并说明该题与不等式的哪一条性质相关。

（1）若x+3>6，则根据不等式性质可得x         3;

（2）若x-2<3，则根据不等式性质可得x         5。

3.如>0，求x的取值范围。

前两大题均与不等式的基本性质有关，需要学生根据基础知识进行解答，难度相对较低。第三题属于拓展题，是一种关于分数的不等式，也是学生后续会经常接触到的一种题型，该题涉及了分数通分的知识点，所以首先要将分子和分母进行通分，才能找到x的取值点，之后在数轴中将其标出，如图3所示。

由于不等式大于0，所以在4的右边可以取任意一个数，如将5带入式中，得到的结果大于0。在数轴中，曲线部分在4的右边部分，以及-1的左边部分均处在数轴的上方，根据这一规律以及不等式的性质，就可以得知x的取值范围为（-∞，-1）U（0，1）U（4，+∞）。

（六）创设生活情境，增进知识理解

数学教学的生活化设计能够让学生从生活的角度思考数学问题，如此一来解决数学问题的过程也是在解决生活问题，能够让学生深刻体会到数学的实际应用价值，并学会从多个角度思考。

如创设问题情境：小莹和小光拿着一个水壶去打水，小莹的水壶比小光的要小一些，假设两个水壶装满水的时间分别为t1、t2，并且食堂只有一个水龙头有热水，如何安排顺序才能让他们的等候时间最少？最少总时间为多少？

首先提问学生，如何将这个生活题转换为抽象的数学问题？这一过程的本质其实就是将文字语言转变为符号语言，根据题目中两个人的打水顺序以及打水等候时间来建立数学模型。之后再引导学生思考，总时间会有几种情况？如何通过不等式将其表达出来？哪种情况下总时间会最少？

学生会先从两个假设的角度分别出发。

假设一：小莹先打水，T1=t1+t1+t2=2t1+t2

假设二：小光先打水，T2=t2+t2+t1=2t2+t1

将两个结果作差可以得到T1-T2=2t1+t2-（2t2+t1）=t1-t2。

由于t1

生活化的情境探究活动，能够提高学生的探究兴趣，在数学探索的过程中发现与不等式相关的更多知识，以及知识在生活中的应用。同时，这一教学过程更加侧重知识的生成过程，能让学生体会到数学的趣味性和应用价值，体会到学习的乐趣。

三、教学反思

对于不等式的性质，从学习难度上来看相对较为简单，但却关系着学生后续的数学学习，所以这也是数学教學中的一个重点。不等式性质的本质其实就是对数的认知，这对于学生来说从小学就已经开始了，不管是认识自然数、分数、整数还是小数、百分数，实数的大小是客观的、既定的。在实数集中，规定一个关系时通常用不等号或等号来表示，不等式的基本性质包括对称性、传递性、加法单调性（同向不等式可加性）、乘法单调性、同向正值不等式可乘性、正值不等式可乘方、正值不等式可开方、倒数法则等。例如，针对数集M的任意三个数a、b、c，若a>b，则a+c>b+c，且c>0，而a×c>b×c。

在教学过程中，不等式性质的学习比较考验学生对数大小的理解与判断，直观体现在不等号方向上，尤其是不等式两边同时乘以或除以同一个负数时，根据不等式的性质4可以得知不等号的方向会发生转变，而学生在观察或计算时往往难以体会到这一原理，因此对性质4的理解可能会产生一些疑问或不通的地方，从抽象的数学活动中探索数学结论具有一定难度。数有大小之分，同样也有正负的区别，需要从学生现有的知识经验出发，从知识形成过程着手干预，才能让学生真正理解不等式的性质，掌握知识迁移能力，为后续的数学学习打下基础，也掌握学习数学的正确方法。不等式的性质是一个基础概念知识，在教学过程中也要让学生体会到知识的形成过程，通过自己的思考和努力得到的答案，往往比教师直接说出来更有价值，也能让学生体会到自主学习的成就感与获得感。因此，在数学教学中，我们要重视学生基础知识的积累与技巧的训练，为学生提供更自由的探索空间，安排适当的、必要的讨论与探究项目，让他们对所学的内容有比较深入的了解与把握，进而养成良好的学习习惯，并在此过程中让学生感受到“数式通性”，并训练类推思维。

（作者单位：陕西省渭南市杜桥中学）

编辑：常超波