黄河水沙监测数据分析与模型构建
蒲宝卿
研究黄河水沙通量的变化规律对沿黄流域的环境治理、气候变化和人民生活的影响,以及对优化黄河流域水资源分配、协调人地关系、调水调沙、防洪减灾等方面都具有重要的理论指导意义.
目前许多水利及相关专家都高度关注黄河调水调沙问题,不断研究探索如何降低黄河河床,改变黄河地上悬河的现象.邱学绍等[1]采用SAS软件作线性回归,确定了排沙量与水流量的函数关系,给出了SAS回归模型.饶明贵等[2]依据灰色数学理论,从等时距GM(1,1)模型理论出发,建立了水流量和排沙量的非等时距GM(1,1)模型.张愿章等[3]运用灰色系统理论,采用DGM、Verhu lst模型建立了流量与小浪底水库排沙速度之间的关系,并运用GM(1,1)残差模型提高模拟精度.韩中庚[4]建立三次B样条数学模型,可用于研究黄河水沙通量问题.曹明伟等[5]通过对黄河水流量和排沙量变化过程的分析得到函数关系,根据插值和拟合理论,利用Matlab软件得到排沙量与时间、排沙量与流量的函数关系式,并进行数值积分得到总排沙量.这些模型的建立与预测分析都为制定黄河调水调沙的实施政策提供了参考.
本文根据小浪底水库下游黄河某水文站2016—2021年的水位、流量与含沙量等实际监测数据[6],设计实验、建立模型进行预测,最终提出了水沙通量监测的优化策略.
1 实验设计
一是构建含沙量随时间变化图,以及含沙量与水位、水流量关系的散点图.在此基础上确定含沙量与各因素之间的关系,通过相关性分析、回归分析等进行量化分析.水沙通量的突变性可以使用Mann-Kendall非参数检验,确定水沙通量时间序列的突变年份.水沙通量时间序列的长期趋势、规律的季节项、不规律的周期项可以使用奇异谱分析(Singular Spectrum Analysis,SSA)进行分解.
二是对季节项和周期项计算周期时间,将季节项、周期项与实际的气候规律、政策因素等进行关联,以便更深入研究水沙通量的变化规律.对奇异谱分解的每个项分别进行分析预测,在每个项规律明确的情况下,直接使用相应的函数进行拟合,在规律不明确的情况下,使用长时间序列预测(Long-Term Series Forecasting,LTSF)进行预测.
三是根据调水调沙前后河底高程的变化规律分析小浪底水库调水调沙的实际效果,进而通过回归分析构建河底高程变化与排沙速度的关系.根据排沙速度的预测值和排沙速度与河底高程变化规律,预测未来10年河底高程的变化.
2 模型的建立与求解
2.1 含沙量与时间、水位、水流量的关系
①含沙量与时间的关系.因不同年份含沙量的平均值差异较大,为方便展示每年内含沙量随时间变化规律,首先绘制含沙量随时间变化图如图1所示.从图1可以看出,大部分年份含沙量数据在6—7月份间存在峰值,可能受小浪底水库调水调沙政策的影响.2016—2021年年均含沙量分别为1.012 5 kg/m3、1.045 1 kg/m3、6.544 1 kg/m3、5.764 5 kg/m3、6.991 6 kg/m3、5.502 8 kg/m3.含沙量在2016—2017年相对较低,而在2018年显著提高,并在2018—2021年期间保持相对平稳.

图1 2016—2021年含沙量随时间变化图
②含沙量与水位的相关性分析及回归分析.分别对2016—2021年各年份的含沙量与水位数据绘制散点图,两者的线性回归分析和相关性分析分别如图2及表1所示.
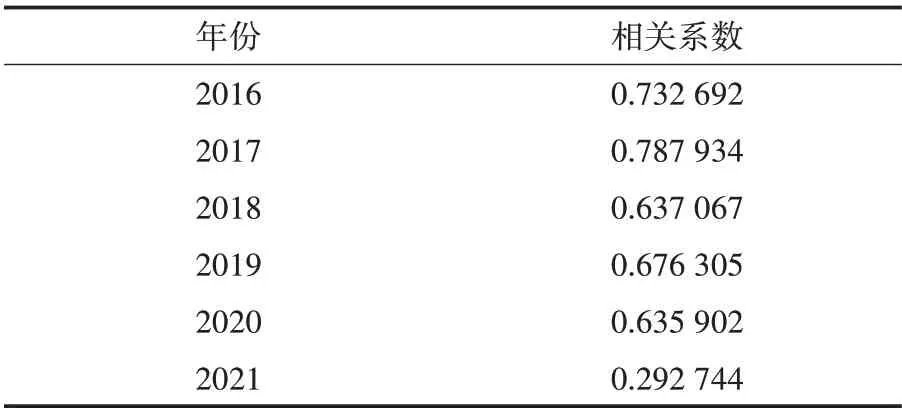
表1 含沙量与水位的相关系数

图2 含沙量与水位散点图及线性回归分析
从图2和表1可以看出,含沙量与水位存在较强的线性关系.2016—2020年,线性函数拟合优度在0.40~0.62之间,但是2021年的拟合优度仅为0.082 113.2016—2020年含沙量与水位相关系数均大于0.63,两者存在显著的正相关性.2021年含沙量与水位相关系数仅为0.292 744.
③含沙量与水流量的关系.分别对2016—2021年各年份的含沙量与水流量数据绘制散点图,对两者的线性回归分析和相关性分析分别如图3及表2所示.
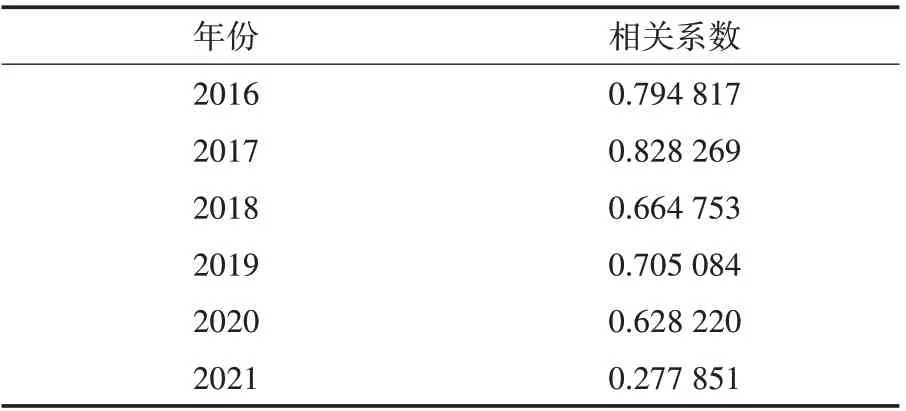
表2 含沙量与水流量的相关系数
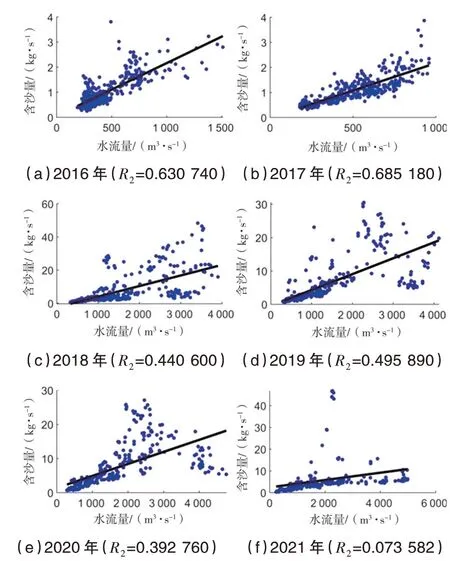
图3 含沙量与水流量散点图及线性回归分析
从图3和表2可以看出,水流量与含沙量的相关系数相对水位更高,其中2017年两者的相关系数达到0.828 269.含沙量与水位的相关性可能是含沙量与水流量相关性的衍生[7].
④总水流量和总排沙量估计.含沙量的观测数据相对水位和流量观测数据存在大量缺失,为了更准确地评估总排沙量,使用线性插值补全缺失的含沙量观测数据.另外,为了控制每天观测次数的不同对总水流量和排沙量的影响,使用每天观测值的均值代表当天的观测值.2016—2021年年总水流量和年总排沙量的估计值如表3所示.
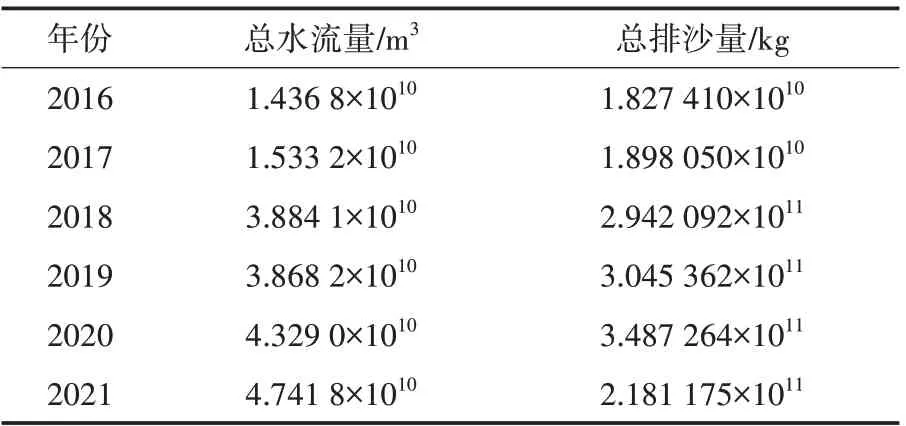
表3 2016-2021年年总水流量和年总排沙量估计值
从表3可以看出,总水流量在2016—2021年期间总体呈现上升趋势,2021年该值估计为4.741 8×1010m3.总排沙量在2020年达到峰值,数值为3.487 264×1011kg.
2.2 水沙通量的突变性、季节性和周期性
①水沙通量的Mann-Kendall突变性检验.通过Mann-Kendall非参数检验法对年总水流量和年总排沙量的突变年份进行确认[8],结果如图4所示.从图4可以看出,在年总水流量的Mann-Kendall统计量曲线中,在0.05置信度区间内,UF和UB曲线在2017—2018年相交.年总排沙量在2017年出现交点.因此,相应的时间节点被推断为水沙时间序列的突变年份.
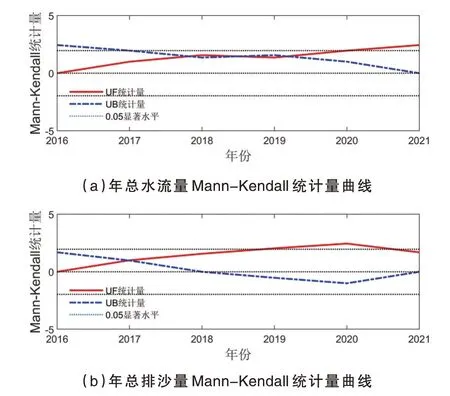
图4 年总水流量和年总排沙量的Mann-Kenda ll非参数检验
②水沙通量的季节性及周期性的SSA.水沙通量的时间序列趋势如图5所示.为发现明显的季节性因素,进一步使用SSA对水流量和排沙量的时间序列进行分解.SSA能够根据观测到的时间序列构造轨迹矩阵,并对此进行分解和重构[9-10],从而提取长期趋势因素、周期性因素、噪声因素等不同成分.
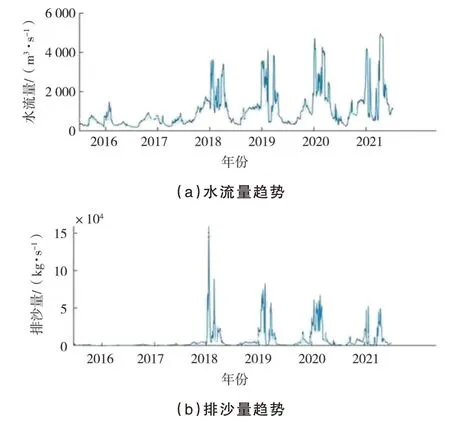
图5 水流量、排沙量趋势的时间序列图
使用Matlab软件内建函数trenddecomp对水流量和排沙量进行SSA,水流量时间序列中发现3个季节性因素,其中方差最大的季节性因素的周期为1年,推断与气候条件相关,对应于枯水季—丰水季循环.排沙量时间序列中方差最大的季节性因素周期同样为1年,与水流量时间序列一致.另外在残差中发现1个周期性因素,2018—2021年每年的6—7月份间,水流量提升了约2 000 m3/s.这一周期性因素推测与小浪底水库的调水调沙政策相关.
2.3 水沙通量的变化趋势及监测方案
前文使用SSA对水流量和排沙量的时间序列进行了分解,发现了水沙通量的长期趋势、与气候相关的季节性因素、与小浪底水库调水调沙相关的周期性因素[11].下文将针对SSA中的长期趋势项、季节项、周期项分别进行拟合预测,然后整合各项预测得到水沙通量的整体预测值[12-13].由于各项的规律性非常明显,结合长短期记忆网络(Long-Short Term Memory,LSTM)在较长期时间下预测的不准确性,本文使用相应的函数直接进行拟合.
①基于SSA的水流量预测.对水流量SSA中解析的趋势项、季节项、周期项等分别进行拟合.其中长期趋势项用线性函数拟合,拟合函数为:
式中:x表示时间,y表示水流量,k和b为待拟合参数.
季节项使用正弦函数与非平稳项联合预测,拟合函数为:
式中:k1,k2,k3,ω为待拟合参数.
调水调沙的周期项通过以下函数定义:
水流量时间序列中长期趋势项和季节项的拟合结果如图6所示.
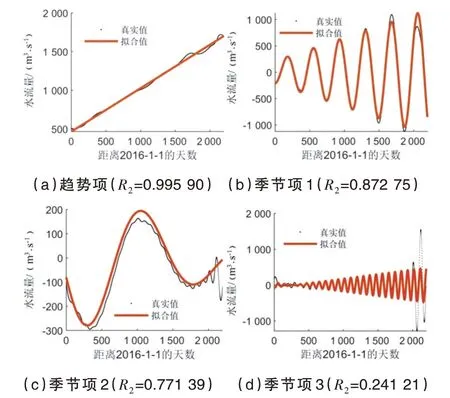
图6 水流量时间序列中长期趋势项和季节项拟合图
通过拟合最终得到的预测函数为:
式中:F(x)表示调水调沙相关的周期项,x表示距离2016年1月1日的天数,y的单位为m3/s.
基于SSA的未来两年水流量预测如图7所示.

图7 基于SSA的未来两年水流量预测图
从图7可以看出,水流量在每年的7月中旬和10月上旬存在两个显著的高峰期.2022年的高峰期预测发生在2022年7月12日和2022年10月2日.2023年的高峰期预测发生在2023年7月8日和2023年10月2日.
②基于SSA的排沙量预测.与排水量预测过程相似,分别对SSA中各成分进行预测并整合,最终得到排沙量的预测函数为:
式中:F(x)表示调水调沙相关的周期项,x表示距离2016年1月1日的天数,y的单位为kg/s.
③采样监测方案设计.根据预测结果,未来两年排水量的峰值出现在7月中旬,排沙量的峰值出现在7月中下旬,另外排水量在每年4月份和1月份存在两个小高峰.因此,为及时掌握水沙通量动态变化,又能最大程度减少监测成本,应在接近预估峰值的时间段提高监测频率[14].另外,可以根据监测数据的累积对水沙通量进行实时预测,动态设定监测频率.
2.4 小浪底水库调水调沙实际效果分析
由于2016—2017年6—7月份间水流量增加不显著,对2019年及以后的相关数据进行分析.观测数据中给出了不同采样时间下起点距离与河底高程的关系,不同时间下河底高程比较如图8所示.
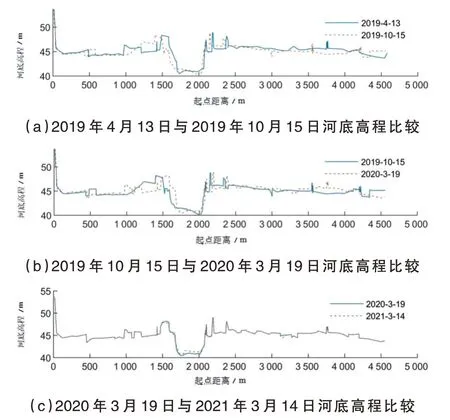
图8 河底高程比较图
从图8可以看出,2019年4月13日、2019年10月15日、2020年3月19日及2021年3月14日的平均河底高程分别为44.969 1 m、43.864 4 m、45.089 8 m、45.023 4 m.因为部分起点距离的数据缺失,仅计算数据存在区段的平均河底高程并绘图.平均河底高程在2019年4月13日至2019年10月15日期间下降了1.104 7 m,期间经历了6—7月份小浪底水库调水调沙期,说明调水调沙对清理河底淤沙有明显效果.而2019年10月15日至2020年3月19日期间无调水调沙,平均河底高程由43.864 4 m上升到45.089 8 m,上升了1.225 4米,说明若不经调水调沙,河底淤沙会快速上升.在2020年3月19日至2021年3月14日大约一年的时间内,平均河底高程几乎无变化,说明6—7月份调水调沙能够保障河底高程处于动态平衡中.
为了研究不进行调水调沙下10年后河底高程预测,直接建立排沙速度与河底高程速度变化的联系.根据表3中的数据和水沙通量的计算结果,绘制河底高程增长速度与排沙速度的关系,如图9所示.两者之间有非常显著的线性相关性.
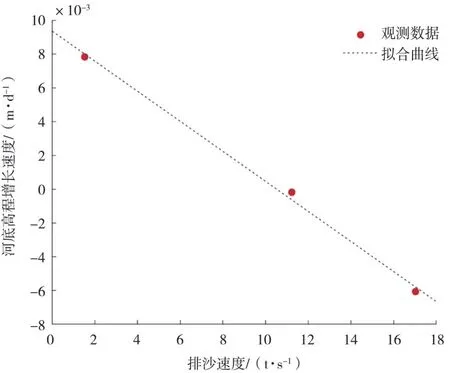
图9 排沙速度与河底高程增长速度图
经线性方程拟合得到,排沙速度与河底高程增长速度的关系为:
式中:x表示排沙速度(t/s),y表示河底高程增长速度(m/d).
当排沙速度为10.519 5 t/s时,河底平均高程将保持不变.排沙速度小于10.519 5 t/s时,河底高程将增加;反之,河底高程将减小.
为预测不进行调水调沙下,10年后河底高程变化,去掉6—7月份的调水调沙代表的周期项后,对排沙速度进行预测,得到未来10年平均排沙速度为7.964 9 t/s时,河底高程平均增长速度为0.002 2 m/d,10年后河底平均高程将增加8.03 m.
3 结语
根据黄河某水文站6年的相关监测数据,建立含沙量与时间、水位、水流量的关系,估算这6年的年总水流量和年总排沙量.分析水沙通量的突变性、季节性、周期性等变化规律,构建模型对水沙通量进行量化分析,使用SSA法对水沙通量时间序列进行了分解,解析出其中的长期趋势、与气候相关的季节性规律和与调水调沙相关的周期性规律.
根据结果对未来两年水沙通量进行预测,在此基础上提出水沙通量监测的优化策略.最后量化河底高程随水沙通量的变化规律,分析了小浪底水库调水调沙的实际效果,可为黄河水沙监测计划及调水调沙政策的制定提供参考.

