圆形抗滑桩-拱形挡土板支挡性能与参数分析

凌贤长, 邢文强, 唐亮, 卢凡, 丛晟亦

(1.哈尔滨工业大学 土木工程学院, 黑龙江 哈尔滨 150090; 2.哈尔滨工业大学 重庆研究院, 重庆 401135; 3.黑龙江省寒区轨道交通工程技术研究中心, 黑龙江 哈尔滨 150090)

目前,桩板式挡土墙的抗滑桩多采用矩形截面形式,其成孔施工往往依赖人工挖孔,施工周期长,且在地层松散,开挖深度较大的情况下,施工安全难以保障。圆形抗滑桩能更好地适应机械化施工,在推进施工进度和提高施工安全性方面的优势使其在桩板墙中的应用成为可能[1],且已有研究表明某些情况下圆形抗滑桩可替换矩形抗滑桩[1-2]。通过将挡土板合理优化为装配式拱形挡板,可进一步提升桩板墙的传力机制和施工便易性。在此前提下,如何对拱形板-圆形抗滑桩支挡体系进行合理的优化设计,使其发挥更好的支挡效果,是需要进行重点关注和深入分析的问题。对此,针对圆形抗滑桩-拱形挡土板体系进行支挡性能分析,以及敏感参数研究,对后续进一步探寻其合理设计与工程应用提供一定参考。针对支挡结构可靠性分析和参数化设计等问题,国内外学者已做了很多相关工作。Babu等[3]提出了一种使用逆可靠性方法获取悬臂板桩墙锚固深度和截面模量的方法,并选用回填土性质等参数作为随机变量进行敏感性分析,评估了设计参数中的不确定性对悬臂板桩墙可靠性的影响。Tan 等[4]进行了针对深层动力压实引起的板桩墙体挠度的有限元参数分析,考虑了墙体嵌入长度、冲击点距离、每次冲击能量、板桩墙支撑侧的土体类型、墙体刚度等参数的影响,确定了有助于减少桩板墙偏转的因素。刘春刚[5]采用有限元方法和解析法对阳安线铁路深路堑边坡的H形桩板墙进行了结构受力和变形分析,对比了H形桩板墙在结构变形协调性、支挡高度、开挖影响范围等方面相对常规深路堑支护结构的优势。唐佳颖等[6]建立了高填方边坡加筋土桩板墙挡墙的有限元模型,分析了边坡的稳定性、潜在破裂面位置以及桩板墙结构的位移和内力,探究了高填方加筋土边坡稳定性的影响因素。朱一铭等[7]采用强度折减法研究了桩身嵌固深度以及支护性能的影响规律,分析了U型板桩支护膨胀土边坡的稳定性。李昭颖等[8]基于数值模拟与极限分析上限法建立了悬臂式挡土墙整体稳定性的计算分析方法,确定了其失稳模式。李哲等[9]采用D-S证据理论建立了支挡型黄土高陡边坡安全评价指标框架体系,得出了边坡变化过程中各参数随时间变化的动态变化规律。李梅等[10]开展了桩板墙现场试验测试和室内模型试验,研究了桩板分担的滑坡推力、桩距等设计参数对桩板结构受力的影响。

已有研究工作主要针对桩板墙结构的支挡性能展开研究工作,结构形式为传统的方桩直板,对圆形抗滑桩在桩板墙中的应用鲜有报道。本文依托某高铁人工路堑边坡桩板墙工程[1],采用圆形抗滑桩替代矩形抗滑桩,将挡土板优化为拱形挡板,提出新型拱形板-桩墙结构。针对桩长、桩径、桩间距、拱形板矢跨比对拱形板-桩墙体系支挡性能的影响效应进行分析,以桩顶水平位移和桩身内力为指标探讨各影响因素的主次顺序,并对拱形板-桩墙体系的工程应用和优化设计提出了初步建议。

1 拱形板-桩墙体系

1.1 拱形板-桩墙有限元模型

文献[1]探讨了圆形抗滑桩代替目前铁路工程中常用的矩形抗滑桩的可行性。研究发现在某些工况下,通过增大桩长,圆形桩板墙可获得与矩形桩板墙相当的支护效果,且二者材料用量基本相同。在此基础上,研究圆形抗滑桩-拱形挡土板体系支护性能。抗滑桩采用圆形截面,桩直径d为1.5 m,桩长L为12 m,桩间距s选为5 m,悬臂段高度为4 m,采用现浇施工;桩间拱形挡土板采用混凝土预制板。由于二次抛物线线形简单且能较好地吻合桩后土压力分布,因此挡板拱轴线取抛物线,矢跨比f/s为0.2,拱形挡土板厚度为0.25 m。

装配式拱形板-桩墙体系抗滑桩采用现浇施工,桩身主体为圆形截面,路堑开挖面以上设置成近似T型截面,圆形桩两侧预留挂板翼缘,路堑开挖面以下为圆形截面(图1)。拱形挡板由多条预制钢筋混凝土条块构成,以搭接的形式与抗滑桩相接。

图1 桩板墙平面布置Fig.1 Detail dimensions of the pile-sheet retaining wall

按照工段边坡实际尺寸建立几何模型,坡度为1∶2.5。为消除边界效应对模拟结果的影响,有限元模型在深度方向上取24 m,为桩长的2倍[1]。有限元模型在宽度方向上选择2个完整的桩间距,两端各沿宽度方向延伸半个挡土板的宽度,计算宽度取15 m,模型详细尺寸如图2所示。土体、抗滑桩以及挡土板采用C3D8单元进行网格划分。考虑到几何模型的复杂性和应力集中现象,对装板周围土单元网格加密处理(图3)。

图2 典型断面剖面图Fig.2 Cross-section of the cutting slope

图3 桩板墙有限元模型网格Fig.3 Finite model of pile sheet retaining wall

桩板墙材料采用C30强度等级混凝土,采用线弹性本构[11],强度参数参照《混凝土结构设计规范》(GB 50010-2010)。粉质黏土层土体本构选用修正剑桥模型(MCC)[12],砂土层选用摩尔库伦模型(MC)[13]。土体参数参照文献[1]选取。混凝土和土体参数见表1。

表1 模型材料参数Table 1 Material properties of soils and concrete

模型假设抗滑桩和挡土板之间没有相对位移,将桩与板之间的接触定义为绑定约束。桩板结构与土体之间通过设置面与面接触来定义接触面之间的相互作用,允许有少量的弹性滑移变形。模型中,边坡土体的上表面设置为自由边界,底面设置为固定约束,其余侧向边界限制法向的位移。对于桩板墙结构,向两侧延伸的半跨挡土板约束对称面的法向位移[14]。

1.2 有限元计算结果及验证

取路基平面以上1 m平面的应力分布云图,如图4所示。应力呈拱状分布从挡板位置往外逐渐扩大,桩间形成了以桩为拱脚的土拱。桩背土体应力比较大,表明由于土拱效应,桩后滑坡推力传递至桩背侧。将抗滑桩悬臂段按一端固定的悬臂梁考虑,锚固段采用“m”法[15],计算抗滑桩内力,与模型计算结果对比如图5所示。

图4 土拱效应示意Fig.4 Contour of soil arching effect

图5 数值模拟结果与“m”法计算结果对比Fig.5 Comparison of numerical results with “m” method

由图5可知通过“m”法计算和数值模拟所得到的桩身弯矩结果分布趋势一致,理论计算得到弯矩最大值比有限元模拟的最大弯矩值稍大。桩身剪力分布也基本一致,均在距离桩顶4 m处,即路堑开挖面处出现最大正值;在距离桩顶9～10 m处出现最大负值。桩身剪力为零点均在距离抗滑桩顶部6～7 m处。但由于“m”法计算将锚固段抗滑桩桩底按照自由约束考虑,因此理论计算结果桩底剪力为零,有限元计算结果桩底剪力非零。

2 装配式拱形板-桩墙支护性能影响因素分析

2.1 桩长对拱形板-桩墙支护性能影响

为探究桩长对路堑边坡开挖后拱形板-桩墙支挡体系抗滑桩水平位移与桩身内力影响,选取不同桩长(10、12、14和16 m)进行分析。同时,保持其他参数不变,桩直径为1.5 m,拱形挡土板矢跨比取0.2,桩间距(抗滑桩圆心之间的距离)为5 m。

从图6中可以看出,桩顶水平位移与桩长呈负相关。10 m长抗滑桩桩身水平位移曲线表明桩身弯曲变形很小,抗滑桩产生较大倾斜;桩长达到16 m时,桩身发生较明显的弯曲变形,倾斜程度变小,桩上各点位水平位移呈非线性变化,由此可知随着桩长增大,抗滑桩弯曲变形增大,抵抗倾覆能力增大。但桩长增加到一定长度后,位移变化趋稳。在所取工况中,桩长为14 m时与16 m时桩顶位移非常接近。换言之,当桩长超过14 m时,通过增大桩长以减小桩板墙水平位移效果较差。

图6 不同桩长下水平位移Fig.6 Displacement of pile under various pile lengths

不同桩长情况下桩身弯矩和剪力的分布如图7所示。由图7可知,桩身弯矩和剪力在不同桩长下分布较为一致,桩身剪力和弯矩随桩长的增大而增大,桩身最大弯矩和桩身零剪力位置一致。总体来看,桩长对抗滑桩悬臂段弯矩和剪力影响较小,主要影响桩锚固段内力。与位移变化趋势类似,当桩长超过14 m之后,弯矩和剪力增加的幅度变小。说明到达一定长度后,对桩身内力影响有限。因此,实际工程中一味通过增加桩长提高支护性能难以达到理想的效果,应根据工程实际需要确定适宜的桩长。

图7 不同桩长下桩身内力Fig.7 Internal forces of pile under various pile length

2.2 桩径对拱形板-桩墙支护性能影响

为分析抗滑桩直径对装配式拱形板-桩墙支护性能影响,选取桩长为12 m,拱形挡土板矢跨比为0.2,桩间距为5 m的工况,分别取桩直径为1.5、1.6、1.7、1.8和1.9 m进行计算。图8为不同桩径下抗滑桩水平位移变化情况。各工况下桩底位移几乎保持不变,桩顶水平位移与桩径呈正相关,桩径由1.5 m增大到1.9 m时,桩顶水平位移减少约22%。桩径在1.5～1.9 m变化时,根据位移曲线斜率可知,桩体发生弯曲变形,桩径越小,弯曲变形越大。在桩长和其他条件一致时,上述差异的主要原因是桩径的不同导致桩身抗弯刚度的差异,桩径越大,抗弯刚度越大,位移和变形越小。

图8 不同桩径下水平位移Fig.8 Displacement of pile under various pile diameters

不同桩径下桩身弯矩和剪力变化见图9。桩身弯矩和剪力均随桩径的增大而增加,变化幅度递减。弯矩和剪力的极值点并不随桩径的变化而变化,桩身最大弯矩位置与桩身零剪力点位置相同。

图9 不同桩径下桩身内力Fig.9 Internal forces of pile under various pile diameters

2.3 桩间距对拱形板-桩墙支护性能影响

为考虑抗滑桩桩间距对拱形板-桩墙支护性能影响,选取桩长为12 m,桩直径为1.5 m,拱形挡土板矢跨比为0.2,分别取桩间距为3、4、5、6和7 m进行计算。

不同桩间距下桩水平位移变化如图10所示。桩顶水平位移与桩间距呈正相关,桩底位移与之相反。根据位移曲线的斜率可知,随着桩间距的增大,抗滑桩弯曲变形也随之增加。

图10 不同桩径下水平位移Fig.10 Displacement of pile under various pile spaces

不同桩间距下桩身弯矩与剪力的分布如图11所示。桩身内力受桩间距影响较为显著,桩间距越大,桩身弯矩和剪力越大,但分布趋势基本一致。桩身内力在一定桩间距范围内较敏感(3～5 m),受桩间距影响较大,超出该范围,影响效果减弱。由此可知,桩间距设置过小,支护效果虽好,但设计过于保守会造成不必要的浪费;桩间距设置过大,无法达到理想的支护效果,也是一种资源的浪费。因此实际工程需将桩间距控制在合理的范围之内。

图11 不同桩径下桩身内力Fig.11 Internal forces of pile under various pile spaces

2.4 拱形板矢跨比对拱形板-桩墙支护性能影响

取桩径为1.5 m,桩长为12 m,桩间距(抗滑桩圆心之间的距离)为5 m的工况,分别取拱形挡土板矢跨比为0.1,0.2,0.3,0.4,0.5和0.6进行分析。

由图12可见,桩顶水平位移与拱形挡土板矢跨比呈负相关,桩底位移变化很小。桩水平位移随矢跨比增大而减小,减小的幅度逐渐降低。当拱形挡土板矢跨比在0.1～0.6时,桩顶水平位移减小约12.3%,而从0.1增长至0.3的过程中,桩顶水平位移减小约7.2%。

图12 不同矢跨比下水平位移Fig.12 Displacement of pile under various rise-span ratios

不同矢跨比下桩身弯矩和剪力各自呈相似趋势分布,均与矢跨比呈负相关(见图13)。矢跨比增加,桩身内力减小,但下降趋势渐缓。矢跨比从0.1增大到0.6,最大弯矩减小12.1%,而矢跨比从0.1增加至0.3时,最大弯矩减小6.8%。由以上分析可知,增加拱形挡板矢跨比在一定范围内对支护效果提升较为明显,超过这一范围提升效果明显减弱。另外,矢跨比过大不仅增加施工难度,而且增加所需开挖的土方量和构件所需圬工量。因此,拱形挡板矢跨比适宜控制在0.2～0.3。

图13 不同矢跨比下桩身内力Fig.13 Internal forces of pile under various rise-span ratios

3 基于正交试验设计的拱形板-桩墙支护性能分析

3.1 拱形板-桩墙支护性能影响因素正交试验设计

正交试验可获得各影响因素对评价指标的影响程度[16]。正交表是进行正交试验设计时用来确定方案组合的工具,根据所优化的问题,由影响因素、因素水平以及评价指标所组成。

依上述,桩长不同水平分别取10,12,14和16 m;桩径不同水平分别取1.5,1.6,1.7和1.8 m;桩间距不同水平分别取3,4,5和6 m;拱形挡土板矢跨比不同水平分别取0.2,0.3,0.4和0.5。根据试验影响因素和水平情况,采用4因素4水平的正交试验,进行16次试验。试验因素水平表和正交表分布见表2和表3。

表2 因素水平表Table 2 Parameter classification

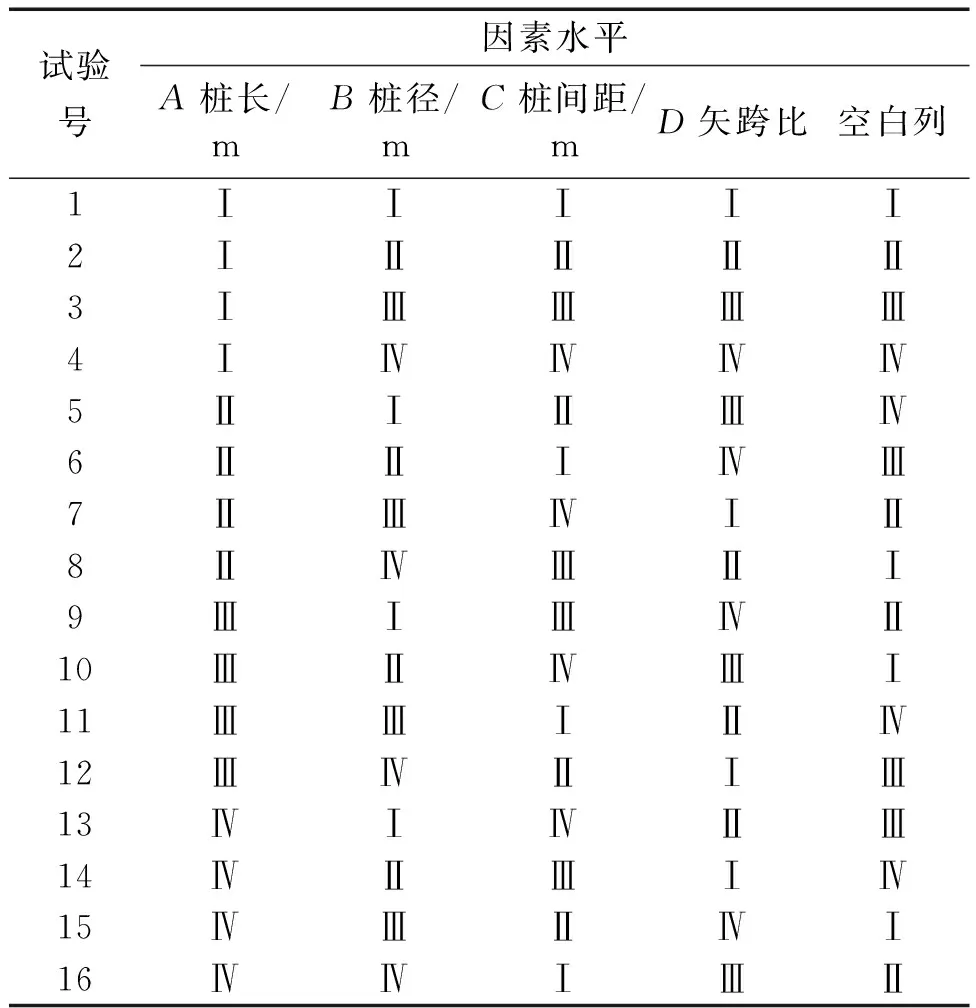
表3 正交表Table 3 Orthogonal test planning

3.2 拱形板-桩墙支护性能正交试验结果分析

根据4因素4水平的正交试验设计,对拱形挡土板桩板墙进行分析,正交试验结果表见表4。根据正交试验结果,分别对各因素进行极差分析和方差分析。极差分析结果如表5～7所示,其中Kij为i因素在第j水平试验之和,R为因素不同水平的极差,R越大说明该因素对考核指标影响越大。另外,为了直观反映各试验因素对考察指标的影响程度,给出试验因素水平和考察指标趋势图(图14)。落差越大影响程度越大,为主要因素;落差较小的因素则为次要因素。根据各因素极差大小排列,由图14可知:对于桩顶水平位移,桩身弯矩和桩身剪力等考察指标,各因素影响的主次顺序均为:桩间距>桩长>桩径>矢跨比。

表4 正交试验结果表Table 4 Orthogonal test results

表5 桩顶最大水平位移极差分析结果Table 5 Orthogonal test results of displacement on the pile head

表6 桩身最大弯矩极差分析结果Table 6 Orthogonal test results of maximum bending moment

表7 桩身最大剪力极差分析结果Table 7 Orthogonal test results of maximum shear force

图14 各因素影响水平变化趋势Fig.14 Degree of parameter influence

方差分析通过F检验得出因素对考察指标是否具有显著性[17]。检验水平取α=0.025和α=0.05。根据正交试验结果,各因素方差分析结果见表8～10。查F分布表得,F0.01=29.46,F0.05=9.28。当F≤9.28时,影响因素不显著;当9.2829.46时,影响因素高度显著。由表中数据可知,以桩顶水平位移作为评价指标,桩长和桩间距F值大于F0.01,因此桩长和桩间距对桩顶水平位移的影响为高度显著;以桩身最大弯矩为评价指标,桩长和桩间距F值大于F0.05,小于F0.01,因此桩长和桩间距对桩身最大弯矩的影响显著;桩径和拱形挡土板矢跨比对各评价指标的影响为不显著;以桩身最大剪力为评价指标,桩长对桩身最大剪力的影响为显著,桩间距影响为高度显著,桩径和矢跨比的影响为不显著。

表8 桩顶位移方差分析结果Table 8 Results of variance analysis of displacement at pile head

表9 桩身最大弯矩方差分析结果Table 9 Results of variance analysis of maximum bending moment

4 结论

1) 桩长与桩身内力大小呈正相关关系,与桩顶水平位移呈负相关关系。随着桩长增大,桩水平位移与桩身内力的变化幅度均减小。当桩长超过14 m时,桩长对抗滑桩位移与内力的影响可忽略。

2) 随着桩间距增大,桩水平位移增大但变化幅度逐渐减小,弯曲变形增加。桩身内力受桩间距影响显著,桩间距越大,桩身弯矩和剪力也越大。

3) 拱形挡土板矢跨比增大时,桩顶水平位移减小,桩底位移基本不变,桩身弯矩和剪力均减小。综合考虑开挖土方量和构件所需圬工量,拱形挡板矢跨比控制在0.2～0.3较为适宜。

4) 以桩顶水平位移、桩身最大弯矩和剪力作为考察指标,影响因素主次顺序为桩间距>桩长>桩径>矢跨比。采用拱形挡土板-桩墙对边坡进行支护时,设计重心为桩间距和桩长的大小。桩径对支护性能的影响程度相对较弱,增大桩径提高圬工量,但支护性能的提升有限。

另外,实际工程中,挡土结构的支护性能不可避免地受地下水水位和气候条件(降雨与冻融作用等)等影响,后续研究将聚焦这些因素对所提出的新型拱形板-桩墙支挡体系支护性能的影响。