挖掘机自动挖掘轨迹规划与动态优化控制
周有明,刘凯磊,3,殷鹏龙,康绍鹏,强红宾,3
(1.江苏理工学院机械工程学院,江苏常州 213001;2.国机重工集团常林有限公司,江苏常州 213136;3.江苏大学流体机械工程技术研究中心,江苏镇江 212013)
0 前言
液压挖掘机作为一种功能强大且使用最为普遍的传统工程机械,在工业建设领域中扮演着极其重要的角色[1-2]。随着人类社会对挖掘机需求的不断提高,使得挖掘机的应用环境也越来越多样化,人们对挖掘机的操作要求也越来越高,传统的液压挖掘机在一些领域凸显出越来越多的问题[3]。例如液压挖掘机在不可视环境下挖掘施工或者复杂折线工程进行作业时,对挖掘精度往往会有很大的要求;另外,对驾驶员脑力和体力消耗较大,长时间工作易造成驾驶员疲劳,甚至事故的发生。因此,对工程机械领域为代表的液压挖掘机进行自动化改造,实现自动挖掘运动轨迹规划控制技术的应用已经越来越迫切和必要。
目前,国内外众多的科研人员对挖掘机自动化进行了相关研究。HAGA等[4]探究了挖掘机的智能挖掘控制系统,采用了激光测距仪,利用位置闭环控制实现对挖掘作业的自动控制。LEE等[5]针对挖掘机器人,基于运动学和雅克比矩阵进行轮廓控制研究。SU和CHENG[6]提出了一种基于梯度分析的运动优化方法,使得自动挖掘机可以获得更好的轨迹规划。郭晓光等[7]针对挖掘机轨迹规划控制系统设计,采用有限状态机和模糊逻辑的思想,通过MATLAB中的Stateflow(状态流)和Fuzzy Logic(模糊逻辑)工具箱对挖掘机轨迹规划控制系统进行了设计并获得可靠的结果。付荣等人[8-9]采用分段多项式插值对挖掘机进行时间最优轨迹规划并取得良好的成效。代瑞恒等[10]通过引入正态分布概率密度函数进行改进量子遗传算法,以最短时间为目标函数,对挖掘机器人关节运动轨迹进行了优化。然而多数学者是从运动学角度研究挖掘机器人轨迹规划,未考虑由于负载力波动而引起各个驱动液压缸输出力的变化过大,导致液压缸运动控制精度过低,从而影响复杂运动轨迹的实现。因此,如何在液压挖掘机轨迹规划中,将各驱动液压缸输出力与运行轨迹相联系,从而便于轨迹运动控制,是液压挖掘机自动挖掘的关键因素之一。
针对挖掘机器人的动力学特性,李海虹、林贞国[11]运用了n次多项式法、傅里叶级数拟合法以及分段多项式插值法对一条T形路径进行一般轨迹规划,将规划前后的动力学特性进行对比,得出函数拟合法的轨迹规划结果分析结论。何经良[12]将对数螺旋曲线轨迹应用和机器人学相关理论相结合,建立了挖掘机的运动学和动力学方程,分析动力学特性的变化影响。王勇等人[13]采用奇异摄动复合控制策略,将挖掘机器人系统分为快、慢2个独立子系统,分别为其设计控制器,加和后作为整个系统的控制输入,进而分析关节柔性及其大小对关节轨迹的影响。文献[14-16]运用了机器人技术以及理论力学对液压挖掘机的铲斗末端建立相关的动力学数学模型,基于液压控制技术、模糊控制理论完成对液压挖掘机铲斗末端轨迹控制试验的研究。
综上所述,本文作者以液压挖掘机为研究对象,建立液压挖掘机工作装置运动学和动力学数学模型。通过五次多项式插值方法将运动轨迹离散,采用MATLAB编写基于动力学模型的离散运动轨迹程序,并将计算结果与ADAMS仿真结果进行对比,最终确定动力学模型参数;其次,建立基于动力学模型的Simulink和ADAMS联合仿真模型,在动态控制中,采用PD控制方法进行运动轨迹联合仿真,研究液压挖掘机自动挖掘轨迹规划权重对稳定性、精确性的影响,从而为后续试验提供理论依据。
1 液压挖掘机模型的建立
液压挖掘机的基本结构如图1所示。液压挖掘机由底座、动臂、动臂液压缸、斗杆、斗杆液压缸、铲斗、铲斗液压缸等组成。该液压挖掘机底座1固定于地面,动臂2底端铰接于底座1上点O,动臂液压缸3底端铰接于底座1上点A,动臂液压缸3活塞杆一端铰接于动臂2上点B,斗杆液压缸4底端铰接于动臂2上点C,斗杆液压缸4活塞杆一端铰接于斗杆5上点D,动臂2另一端铰接于斗杆5上点E,铲斗液压缸6底端铰接于斗杆5上点F,铲斗液压缸6活塞杆一端铰接于摇臂上点H,斗杆5另一端铰接于铲斗7上点J。其工作原理为:通过控制各组液压缸的运动即可完成各部件之间的相对运动,从而完成铲斗挖掘、联合挖掘等作业工况。在自动挖掘过程中,通过协同规划各组液压缸的动作,可以实现复杂的运动轨迹。
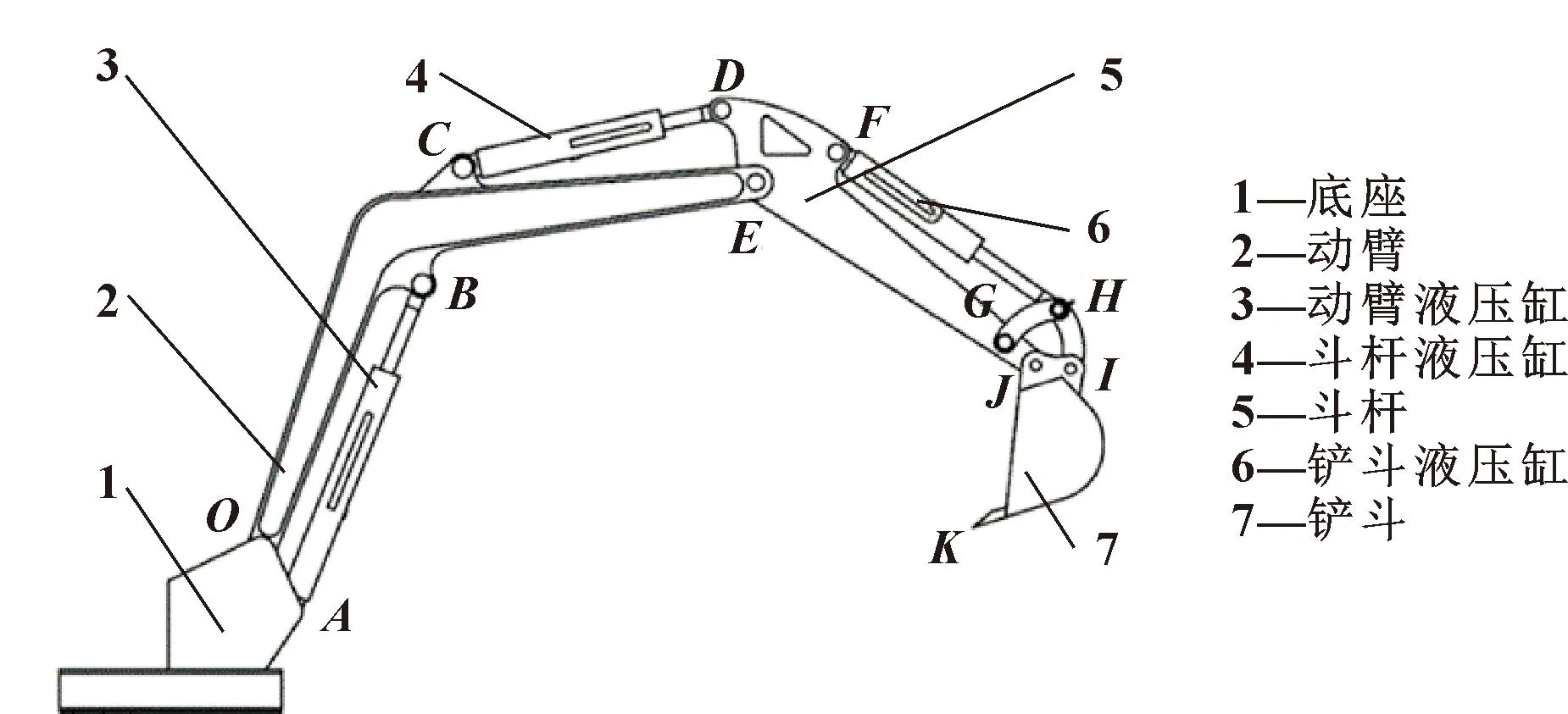
图1 液压挖掘机简图
2 液压挖掘机的运动学模型
根据机器人理论,将液压挖掘机的工作装置建立在D-H坐标系中,采用齐次变换描述挖掘机工作装置各连杆坐标系之间空间的几何关系时,其连杆变换矩阵i-1iT为
(1)
式中:θi表示为第i个关节转角;ai-1表示为第i-1个杆件长度;di表示为第i个关节距离;sαi-1表示sinαi-1;cαi-1表示cosαi-1;sθi表示sinθi;cθi表示cosθi。
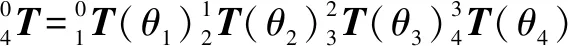
(2)
其中:θ1、θ2和θ3分别为动臂关节变量、斗杆关节变量、铲斗关节变量。

表1 液压挖掘机工作装置连杆参数
3 液压挖掘机的轨迹规划
根据液压挖掘机的一般工作情况,在液压挖掘机工作区域内进行轨迹规划,图2所示为液压挖掘机挖掘路径点。
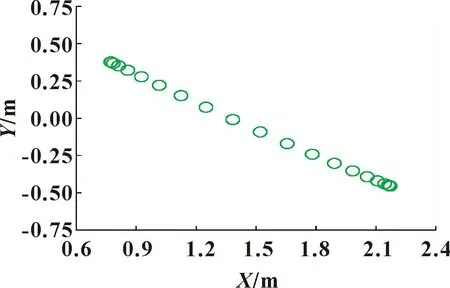
图2 挖掘路径点
以图3所选的挖掘路径点为例,对液压挖掘机机械臂进行轨迹规划研究。对于给定的路径点,分成对应的挖掘过程中的5段轨迹,为了使整个运动过程中关节角度、角速度、角加速度以及关节脉动满足平滑连续的要求,对各关节的5段路径均采用5次多项式插值。
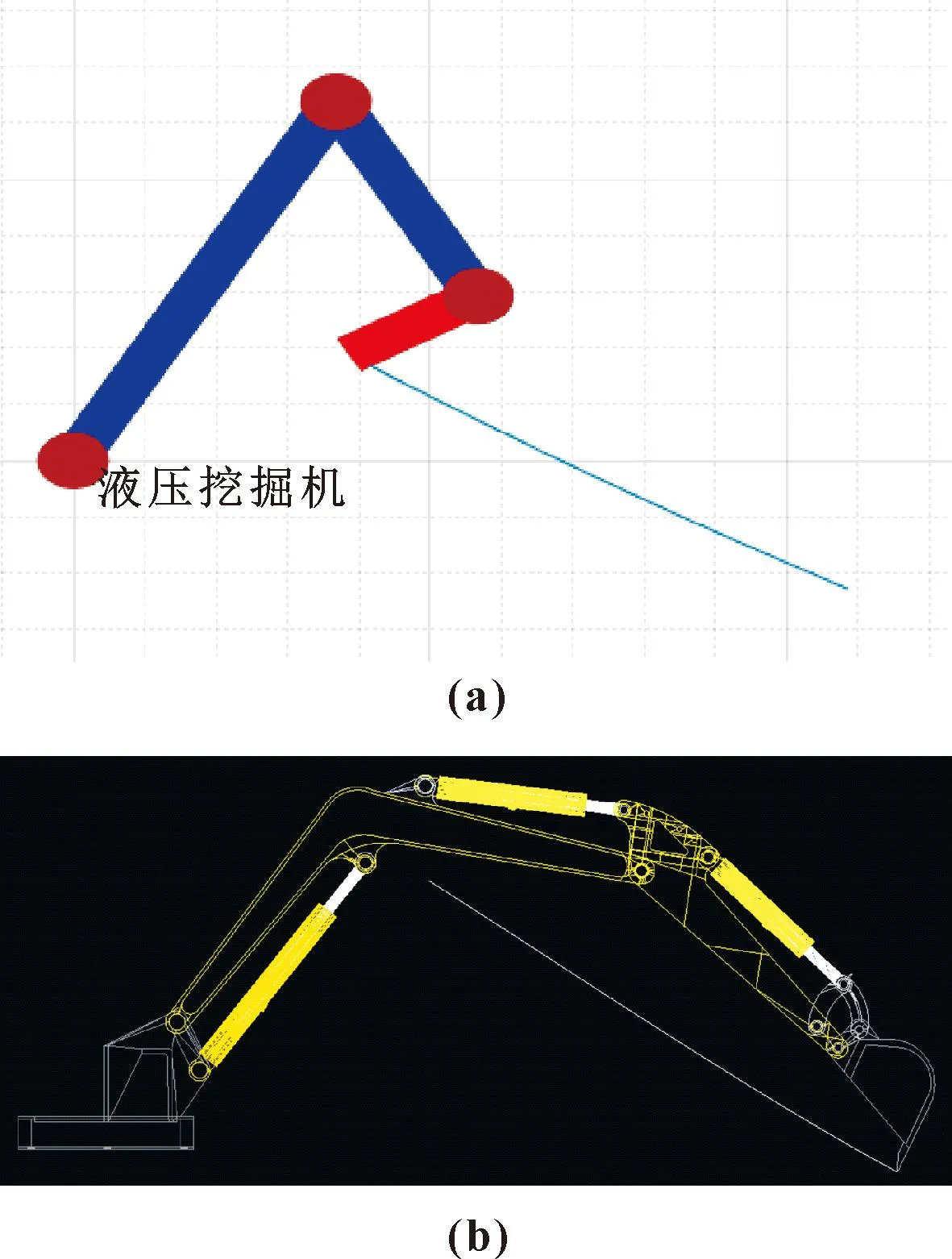
图3 MATLAB(a)、ADAMS(b)液压挖掘机运动轨迹
设挖掘机第i个关节五次分段多项式表达式为
(3)
式中:θik(t)为第i个关节的第k(k=1,2,3,4,5)段多项式插值函数,其中i=2,3,4分别表示动臂、斗杆、铲斗关节;aikw为第i个关节、第k段的多项式系数,w=0,1,2,3,4,5。
选取图3所示的铲斗末端液压挖掘机路径所对应的3组关节角度(n=5)Pi=[pi0,pi1,pi2,pi3,pi4,pi5]。
则五次分段多项式轨迹连续并且经过插值点所需要满足的条件如下:
(1)依次经过给定的关节插值角度且保证连续:
(4)
(2)始末点关节角速度为0且中间插值点处关节角速度连续以及始末点关节角加速度为0且中间插值点处关节角加速度连续:
(5)
(3)中间插值点处关节角加加速度连续以及四阶导数连续:
(6)
根据上式求得五段五次多项式的表达式,可得关节运动时的速度和加速度。
4 液压挖掘机动力学方程
液压挖掘机进行轨迹规划时,不仅要得到液压挖掘机运动学的轨迹规划值,还要尽量减少运动过程中液压缸输出力的突变。为此,在轨迹规划中应用拉格朗日法求解液压挖掘机的动力学方程。
由拉格朗日方程得:
(7)
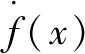
针对液压挖掘机的非线性系统,为了更加直观地表述动力学方程,整理成如下的动力学模型:
(8)
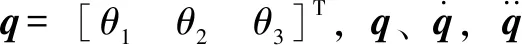
当系统以一定的速度和加速度驱动液压挖掘机时,可通过动力学方程估计出各个关节需要提供的动力。
5 运动学和动力学拟合曲线分析
根据液压挖掘机的运动学五次多项式插值方法将运动轨迹进行离散,采用MATLAB编写了基于动力学模型的离散运动轨迹程序,同时将该模型导入到ADAMS虚拟样机里进行仿真。液压挖掘机基本参数如表2所示。

表2 液压挖掘机基本连杆参数
令液压挖掘机末端沿预设轨迹移动,轨迹上两点之间运动时间设置为0.1 s,仿真时间为20 s,图3所示为MATLAB、ADAMS液压挖掘机运动轨迹。
根据MATLAB程序以及ADAMS虚拟样机得到各个关节的轨迹,对其运动轨迹求一阶导和二阶导得到各个关节角速度和角加速度变化曲线并进行对比分析。
由图4可知:从整体上看,MATLAB 在理想状态下得出的各个关节角速度和角加速度均低于ADAMS仿真结果;对于动臂而言,由于传统液压系统不稳定因素难以控制,导致轨迹路径的初始角速度和初始角加速度出现负值;相对斗杆而言,在刚柔耦合的作用下尤为突出,角加速度在始末位置的突变显著,ADAMS仿真角速度达到的峰值高于MATLAB且超前1 s;对于铲斗而言,在空载的情况下,前10 s轨迹运动比后10 s移动快并趋于稳定。
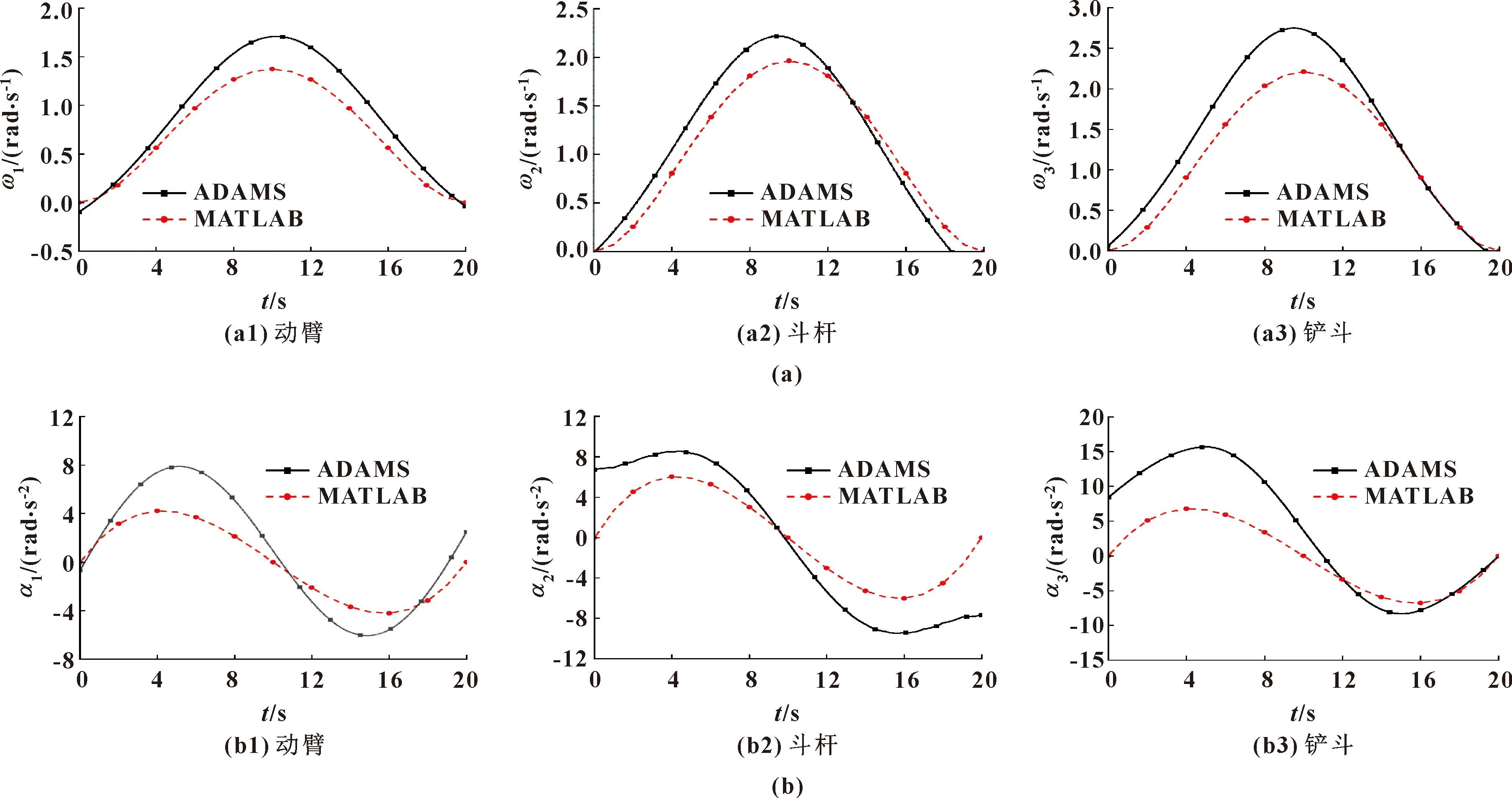
图4 液压挖掘机角速度(a)、角加速度(b)对比
利用计算机对液压挖掘机动力学方程进行推导,并将各个关节的运动轨迹转化为各个液压缸的输出位移,限于篇幅,详细的动力学方程不在此给出。
如图5所示,MATLAB理论公式基于理想状态,因此在刚柔耦合的作用下,液压缸输出力要远远大于理想值。在传统的液压系统中,输出力难以稳定控制,尤其是动臂液压缸,故动臂液压缸输出位移要大于期望值。为了让液压挖掘机能够到达预设轨迹,斗杆、铲斗液压缸输出位移随之做出相应的补偿修正。
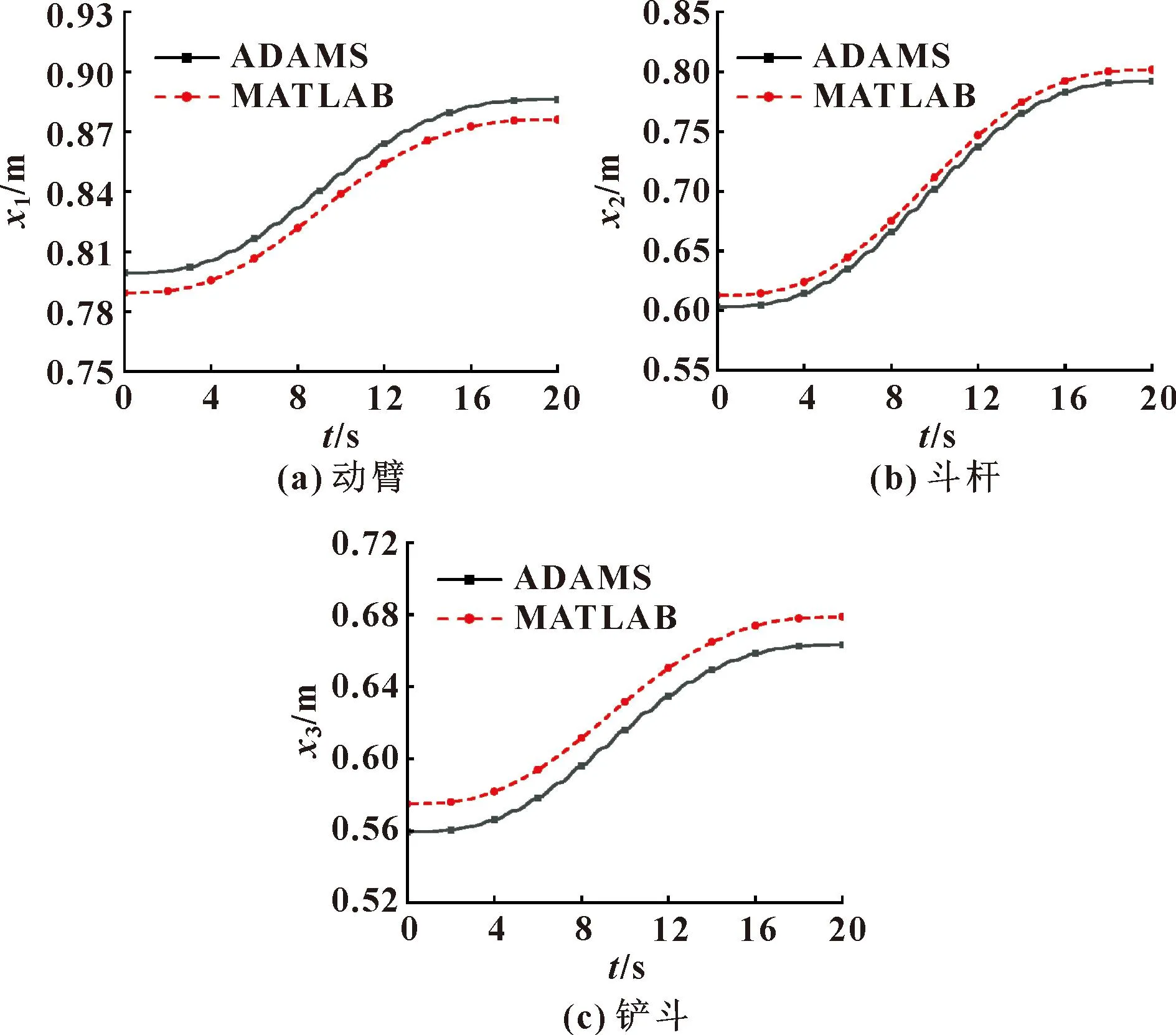
图5 液压挖掘机液压缸输出位移对比
综合角速度、角加速度以及液压缸输出位移变化曲线可知,图6所示的各个液压缸输出力变化规律符合理论。MATLAB理论公式基于理想状态,因此ADAMS仿真结果均大于理论值;其次,动臂液压缸在后半段轨迹中出现抖动,可为后续优化控制器提供切入点。
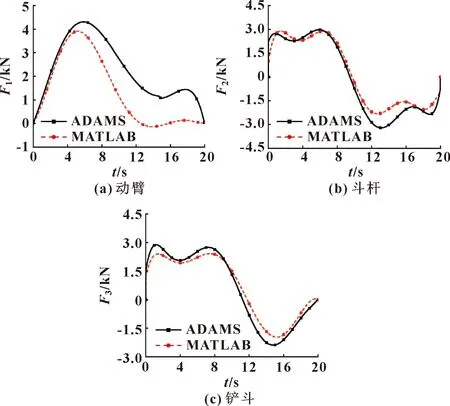
图6 液压挖掘机液压缸输出力对比
6 基于动力学模型的动态优化控制
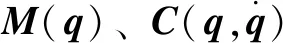
其中轨迹误差表示为
e=qd-q
(9)
可以得到:
(10)
7 联合仿真分析对比
在Simulink里建立PD反馈控制律模型,通过接口设置与ADAMS模型进行联合仿真,图8所示为搭建的部分动力学模型。
将基本参数以模块参数的形式从MATLAB工作区里封装读取,设置交互时间为0.01 s,仿真时间为20 s,仿真结果如图9—11所示。

图9 液压挖掘机液压缸输出位移对比(不同Kp、Kv组合)
通过适当地设定权重Kp和Kv可使轨迹误差更小、更精确。文中采用经验法采集了12组数据,将误差过大的数据剔除,保留6组数据与第5节中的性能曲线对比。动态控制下的联合仿真,可以实时动态反馈液压挖掘机各关节的状态,能够让液压挖掘机到达期望轨迹,其中,Kp和Kv组合为200-5和250-5时更接近期望轨迹,因此还需进一步对比分析。
图10所示为上述6组数据的液压挖掘机液压缸运动收敛趋势。可以看出:Kp和Kv组合为200-5和250-5时,虽在整个仿真过程中,最终收敛趋势都趋于0,但组合为200-5时,相较于组合250-5起始过程要收敛近50%,有利于液压挖掘机稳定精确控制。
如图11所示,综合液压缸输出位移变化曲线对比以及运动收敛趋势对比,动态控制下的联合仿真结果表明液压挖掘机轨迹运行过程中各个液压缸输出力变化规律不仅与理论相等,且能稳定运行,其误差稳定在5%附近。相较于未优化仿真,角加速度在始末位置趋近于0,有效地削减了抖动的影响,提升了轨迹的可执行性,使得液压挖掘机自动挖掘轨迹稳定精确。
8 试验验证
如图12所示,在2T液压挖掘机试验台的基础上开展液压挖掘机运动轨迹控制试验,以验证上述动态控制下PD控制方法的有效性。

图12 液压挖掘机试验台
此试验将Simulink中建立的PD反馈控制律模型通过CAN通道与试验台控制器BODAS进行实时通信,控制效果如图13、14所示。
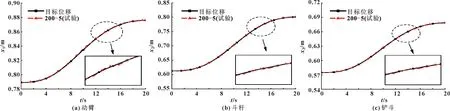
图13 液压挖掘机液压缸目标与试验位移对比
从图13可以看出:轨迹试验中,动臂、斗杆和铲斗液压缸输出位移基本与目标位移一致,轨迹曲线存在波动,虽波动频率较高,但波动幅度较小。结果表明:Kp和Kv组合为200-5的PD控制中各组液压缸输出位移的误差明显减小。
如图14所示,Kp和Kv组合为200-5的PD控制轨迹试验验证了上述各个液压缸在起始时运动收敛趋势的优势,保证了液压挖掘机各个液压缸输出力稳定并贴近目标值。虽然轨迹过程存在一定波动,但Kp和Kv组合为200-5的PD控制能够有效削减抖动带来的影响,而且在实际运动过程中波动并不明显,其误差稳定在5%附近,能够使液压挖掘机自动挖掘轨迹稳定精确,提升了轨迹的可执行性,满足挖掘机的工作要求。
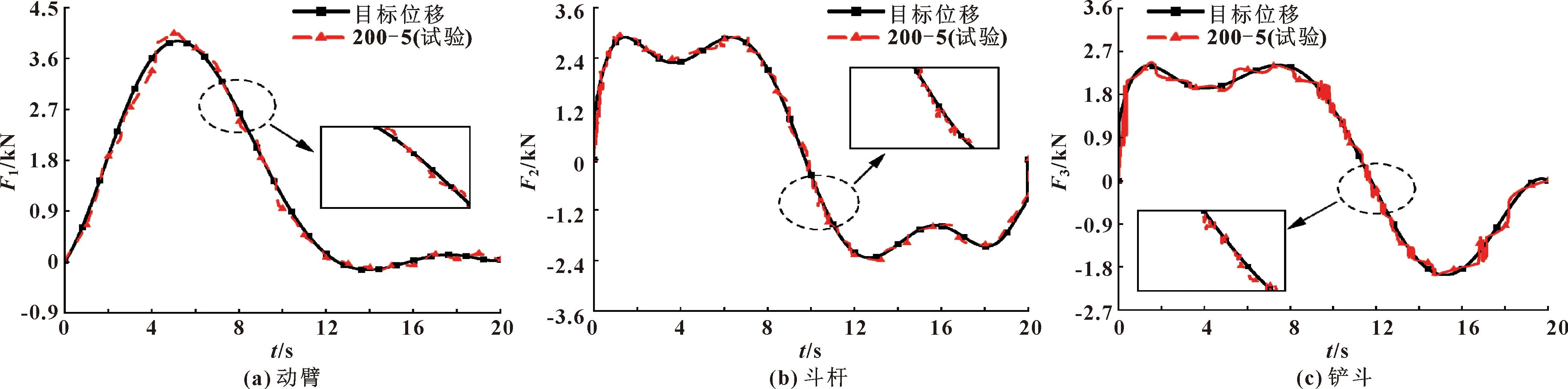
图14 液压挖掘机液压缸目标与试验输出力对比
9 结论
(1)MATLAB程序以及ADAMS虚拟样机求得的角速度、角加速度、液压缸输出位移以及液压缸输出力曲线变化规律均一致,且较好地贴合期望运动轨迹。
(2)由于阀控液压系统的非线性,液压挖掘机轨迹运动中的加速度在始末位置不为0,使得部件启停时各关节会产生较大的冲击,从而引起部件的振动、加剧关节的磨损、降低部件的使用寿命。分析轨迹过程中突变因素,为后续优化控制器提供切入点。
(3)在联合仿真的动力学模型中加入动态控制中的PD控制律,有效地削减了轨迹中突变因素。调整权重得到的收敛趋势相较于未优化的要收敛近50%,各个液压缸输出力变化稳定并贴近理论值,其误差稳定在5%附近,缓解了各关节产生的较大冲击,提升了轨迹的可执行性,使得液压挖掘机自动挖掘轨迹稳定精确。
(4)Kp和Kv组合为200-5的PD控制轨迹试验验证了联合仿真下各个液压缸的运动收敛趋势起始时的优势,保证了液压挖掘机各个液压缸输出力稳定并贴近目标值。虽然轨迹过程存在一定波动,但Kp和Kv组合为200-5的PD控制能够有效削减抖动的影响,而且在实际运动过程中波动并不明显,能够满足挖掘机的工作要求。

