内斜齿轮车齿加工数学模型及实验研究

周鑫，耿龙龙，韩正阳，蒋闯，2 ，王会良

(1.河南科技大学机电工程学院，河南洛阳 471003；2.洛阳科大格尔传动研究院有限公司，河南洛阳 471003)

0 前言

新能源汽车电驱动高转速、小型化、集成化的发展对变速器提出高速化、高功率、轻量化要求，行星减速器具有紧凑、传动平稳、承载能力大等优点而在新能源汽车上普遍使用[1]。内齿轮是行星变速器的核心部件[2]，内齿轮传统上采用插齿加工，单齿加工方法以及切削过程运动空行程造成内齿轮加工效率低，无法匹配市场对内齿轮的需求。近年来，车齿加工技术的发展为上述问题的解决提供了潜在的方案。

在此基础上，本文作者提出新能源汽车用内齿轮车齿加工的方法，实现内齿轮高效、高质量加工，以解决传统插齿加工效率低的问题。根据内齿轮车齿加工原理建立车齿加工的数学模型，以新能源汽车行星减速器内齿轮为例，推导内齿轮齿面方程并进行模拟仿真，通过切齿实验对建立的车齿加工模型进行验证。

1 内齿圈车齿加工原理

基于交错轴啮合原理进行车齿加工。加工过程中刀轴与工件产生轴交角，如图1所示。其大小由工件与车齿刀螺旋角确定。图中：a1为工件回转轴，ac为刀具回转轴；ω1为工件角速度，ωc为刀具角速度。刀具节圆与工件相切于点O，β1为工件螺旋角，βc为刀具螺旋角，Σ为刀具与工件的轴交角。

图1 内齿轮车齿加工原理

车齿加工时，齿轮的齿向l应与刀具齿向同向，因此应满足

Σ=β1-βc

(1)

式中：工件和刀具的螺旋角β1、βc为正时表示左旋，为负时表示右旋；Σ的符号决定刀具的倾角方向。

车齿运动由两部分构成：(1)工件与刀具在点O处的切削运动vc1，由工件回转速度v1与刀具回转速度vc合成；(2)刀具沿着工件轴线的进给运动速度为v。车齿过程中工件与刀具间的运动满足如下关系：

(2)

式中：zc为车齿刀齿数；z1为工件齿数；L为工件螺距。

“浓”造宣传氛围，加强法律法规宣传。深入开展“六进”活动，把食品药品法律法规讲堂搬进企业、搬进社区、搬进农村、搬进学校、搬进医院、搬进商店药店。积极组织 “食品安全宣传周”、“安全用药宣传月”活动，提高相关法律法规普及水平。注重惩教结合，实施轻教严惩的监管机制。同时开展食品药品安全“随手拍”活动，鼓励群众积极举报，落实举报奖励制度。

2 车齿加工模型

2.1 车齿刀模型

车齿刀可以看做一个从前刀面到刀柄变位系数逐渐减小的圆柱斜齿轮，则前刀面上的切削刃可以简化为端面渐开线，如图2所示。rb为端面渐开线的基圆半径，r0为刀具分度圆半径。X1坐标轴为渐开线的起始点，Z1方向与刀具轴线方向重合。

图2 车齿刀数学模型

切削刃上一点P的坐标可以表示为

(3)

(4)

式中：Sa=1时表示左切削刃，Sa=-1时表示右切削刃；φ为渐开线的廓形参数，与渐开线上点P处压力角αp的关系为：φ=tanαp。

坐标系S2中X2为左、右切削刃的对称线，将点P坐标表示在S2坐标系中为

r2(φ)=M21r1(φ)

(5)

式中：

2.2 车齿加工数学模型

建立内齿轮车齿加工模型如图3所示。坐标系S6固连于工件，Z6方向与工件轴线重合。坐标系S3、S4、S5为辅助坐标系，其中Z5和Z6重合；S5平行于坐标系S4；Z3与Z2重合。φc为刀具转角，φ1为工件转角。a为刀具与工件的中心距，ds为切触点位于工件坐标系Z方向的轴向位置。

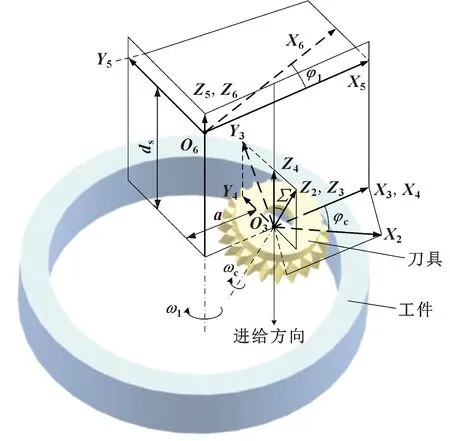
图3 内齿轮车齿加工数学模型

由坐标转换可得：

r6(φ,φc,ds)=M62(φc,ds)r2(φ)

(6)

式中：

M62(φc,ds)=M65M54(ds)M43M32(φc);

由车齿加工原理可知：

(7)

式中：“+”表示左旋内齿轮；“-”表示右旋内齿轮。

式(6)应满足啮合方程：

(8)

2.3 齿廓点求解

车齿齿廓上任意一点Pi应满足式(6)。图4中，OH为点Pi在Z6上的投影点，Hi为点Pi到X6Y6平面的距离，Ri为点Pi所在廓形上的半径。点Pi的表达式应满足：

(9)

图4 齿廓点空间位置

式(9)与式(8)共同组成一组含有3个未知数的三维非线性方程组。通过给定初值可以获得一组精确解(φ，φc，ds)，将其代入式(6)中，可以获得齿面上任意一点的三维坐标。

根据建立的车齿加工数学模型，以某新能源行星减速器内斜齿轮为例，具体参数如表1所示，由式(6)—(9)计算内斜齿轮的齿面点，并在UG中建立了三维模型，如图5所示。

表1 内斜齿轮及车齿刀参数

图5 内齿轮三维模型

3 仿真加工

仿真加工可以有效地验证刀具设计的参数，并对实际加工过程中可能出现的干涉、安装等问题进行预测，提高加工效率。在车齿加工前首先利用Vericut进行仿真加工。

在UG三维软件中对车齿刀廓形进行建模，并将它导入至Vericut中，作为仿真加工的车齿刀具，如图6所示。在Vericut环境中建立内齿轮车齿加工机床，并将刀具与工件分别装配至刀具主轴和工件主轴上，根据车齿加工原理以及刀具的安装参数，编写加工程序进行内斜齿车齿仿真加工，如图7所示。

图6 车齿刀具三维模型

仿真加工过程中没有出现刀具与机床、机床夹具等的干涉现象。仿真加工的内斜齿轮如图8所示。

图8 内斜齿轮仿真加工结果

对比图8、5可知：仿真加工与理论建模的齿轮在齿形、齿向上一致，表明所编制的车齿加工程序是正确的。同时对加工过程中的空行程进行了优化，缩短了加工时间，进一步提高了加工效率。

4 实验验证

根据表1定制了车齿刀具，如图9所示。加工设备采用某公司YK2260NC数控车齿机，该机床能够实现圆柱齿轮的车齿加工。根据优化后的车齿程序进行了车齿加工实验，如图10所示。

图9 车齿刀

将加工的工件经过倒角整理后，采用Gleason650GMS检测中心检测加工精度，如图11所示。测量结果如图12所示。

图11 内斜齿轮测量

图12 误差测量结果

图12分别为车齿加工内齿轮齿距误差、齿形误差及齿廓误差。按照GB/T 10095.1—2008《圆柱齿轮 精度制 第1部分：轮齿同侧齿面偏差的定义和允许值》 计算，加工工件齿距精度为5、6级，齿向精度5、7级，两面齿形精度分别为6、7级。以上误差产生的原因有机床的运动误差、工件的安装误差、刀具的廓形误差等，但均在误差要求范围内，满足热前加工精度要求。测量结果验证了所建立模型的正确性。

5 结语

文中基于啮合理论分析了内斜齿轮车齿加工原理，建立了内斜齿轮车齿加工数学模型，并完成了内斜齿轮齿面推导；通过模拟仿真以及实验完成了车齿加工验证。加工的内斜齿轮精度满足工程要求，验证了所建立模型的正确性。

文中为内斜齿轮的高效车齿加工提供了理论和技术支持，具有一定的理论和应用价值。后续将开展车齿工艺参数的优化，进一步提高刀具的使用寿命和加工效率。