基于刚柔耦合的PCB钻床下钻机构的振动分析与研究

张冬冬，韩雪

(1.南京林业大学工程培训中心，江苏南京 210037；2.皖江工学院土木工程学院，安徽马鞍山 243031)

0 前言

PCB板钻孔逐渐向着多层、高密度、细微化的方向发展。尤其是多层PCB板的应用越来越广泛，对多层板孔的加工质量要求越来越高，多层PCB板层数最多可达52～60层[1]。目前，10层以下的PCB板钻孔精度有很大提高，但10层以上的多层PCB板孔的加工精度仍然有很多不足。随着PCB板层数的增加，孔的加工精度逐步降低。而目前对于高密度多层PCB板不同层数间的孔对位精度要求较高，一般要求孔的层间错位控制在25 μm 以内[2]，所以在PCB板机械钻孔领域，如何提高多层板钻孔精度是目前PCB板钻孔领域备受关注的课题。

PCB钻床主轴系统的研究已经有了一定的进展，如吉林大学的玛嘎拉[3]利用有限元方法建立转子动力学模型，分析了钻头钻孔时影响弯曲变形的因素。裴永臣[4]结合振动钻孔特点，建立主轴系统振动钻削转子动力学模型，给出振动钻削主轴系统动力学性能评价指标。EMA和MARUI[5]对深孔钻削加工过程中切削系统的颤振问题进行了理论分析。KOSMOWSKI 和WELLS[6]提出一种评价印刷电路板用钻头加工钻孔过程中受振动情况的测量系统，但对于PCB钻床下钻机构主轴系统的刚柔耦合效应未充分考虑，对引起钻头振动的柔性振动的研究较少，而主轴系统的柔性振动是引起钻头振动的重要因素之一。

刚柔耦合动力学在柔性机械臂领域的研究比较广泛，主要利用广义拉格朗日方法和模态假设法建立多自由度刚柔耦合机械臂的动力学方程[7-11]。如余峰、陈新元[12]针对N自由度柔性机械臂，提出了一种建立刚柔耦合动力学方程的通用方法。赵亮[13]针对带有末端执行器的柔性机械臂，导出其刚柔耦合动力学方程，并分析了机械臂在不同运动状态下的动力学响应。混合坐标方法在建立刚柔耦合动力学方程时得到了广泛应用[14-19]。王佰超等[20]利用集中质量法建立了半球型锥齿轮副的动力学模型，并分析了其动态传动性能。王博洋等[21]基于小变形假设，利用浮动坐标法，采用多体系统动力学单向递推组集方法，建立了哑铃型航天器的刚-柔耦合动力学模型。然而这些研究中并未对刚柔耦合机械臂或柔性梁带有复杂的平移运动和转动驱动状态下的动力学状态进行分析。在PCB钻孔领域，钻床下钻机构的主轴系统在刚柔耦合状态下的动力学分析与研究还不多，对于下钻机构主轴系统需要考虑其下钻时竖直方向上的下钻运动以及柔性梁主轴柔性振动引起的转动，并考虑其刚性梁和柔性梁的耦合。本文作者针对影响加工多层PCB钻孔精度的主要因素进行分析，考虑下钻机构主轴系统刚柔耦合效应对钻孔振动的影响，建立主轴系统的刚柔耦合动力学方程，并进行分析；找出影响下钻机构主轴系统柔性振动的因素，改善其动力学特性，提高多层PCB板的钻孔精度。

1 影响下钻机构钻孔精度的因素分析

PCB钻床下钻机构主轴系统对孔位精度有着重要影响。由于钻头细长，并且电主轴转速较高、加工的孔径小等特点，所以对钻孔机构的下钻精度要求较高。而目前PCB钻床机械钻孔的质量问题主要体现在以下3个方面：(1)位移偏差，产生孔位偏移，对位失准。这主要是滑板X方向和工作台Y方向的定位误差以及钻孔机构安装误差引起孔位轴线与钻头主轴的偏移，偏移量为s，如图1所示；(2)角度偏差，产生孔位歪斜。对于多层PCB板通孔加工来说，底层板偏差较大。角度偏差产生原因包括：钻孔机构安装角度偏差以及主轴系统刚性不足引起的偏差角α，钻孔过程中的钻头刚性不足引起的钻孔偏差角β。其中角度偏差α越大，钻头在下钻过程中产生的附加弯矩也越大，钻头弯曲产生角度β也越大；(3)振动误差。孔的特点表现为孔壁粗糙、毛刺过大、孔形圆度失真以及孔径失真。这主要与下钻机构中的调心联轴器有关，调心联轴器中的调心轴产生的柔性变形引起柔性振动偏差。该柔性偏差对于多层PCB板中底层板孔的质量产生的影响较大。PCB板层数越多，振动偏差也越大，甚至出现钻头折断。如何提高钻孔机构动态特性、减小柔性振动误差是提高多层PCB板钻孔精度和质量的重要因素。

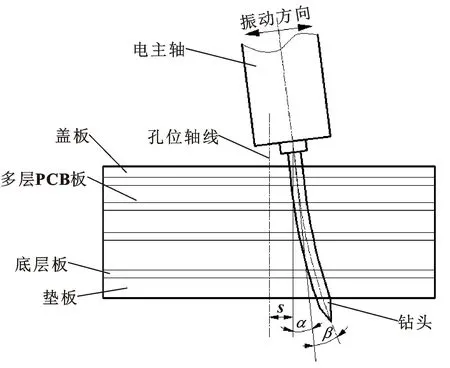
图1 主轴部分钻孔示意

2 刚柔耦合下钻机构主轴系统动力学模型

2.1 钻孔机构结构模型

下钻机构主轴系统的主要结构如图2所示。直线电机连接板由直线电机驱动，带动主轴系统沿着导轨方向实现上下的直线运动，从而带动钻头完成钻孔。连接座固定在连接板上，调心联轴器连接着连接座和电主轴部分，该装置主要实现对主轴部分的调心，配合空气静压轴承对电主轴部分实现调心与固定。调心联轴器为主轴系统重要的核心装置，其动态特性与下钻机构主轴系统钻孔精度有直接关系。

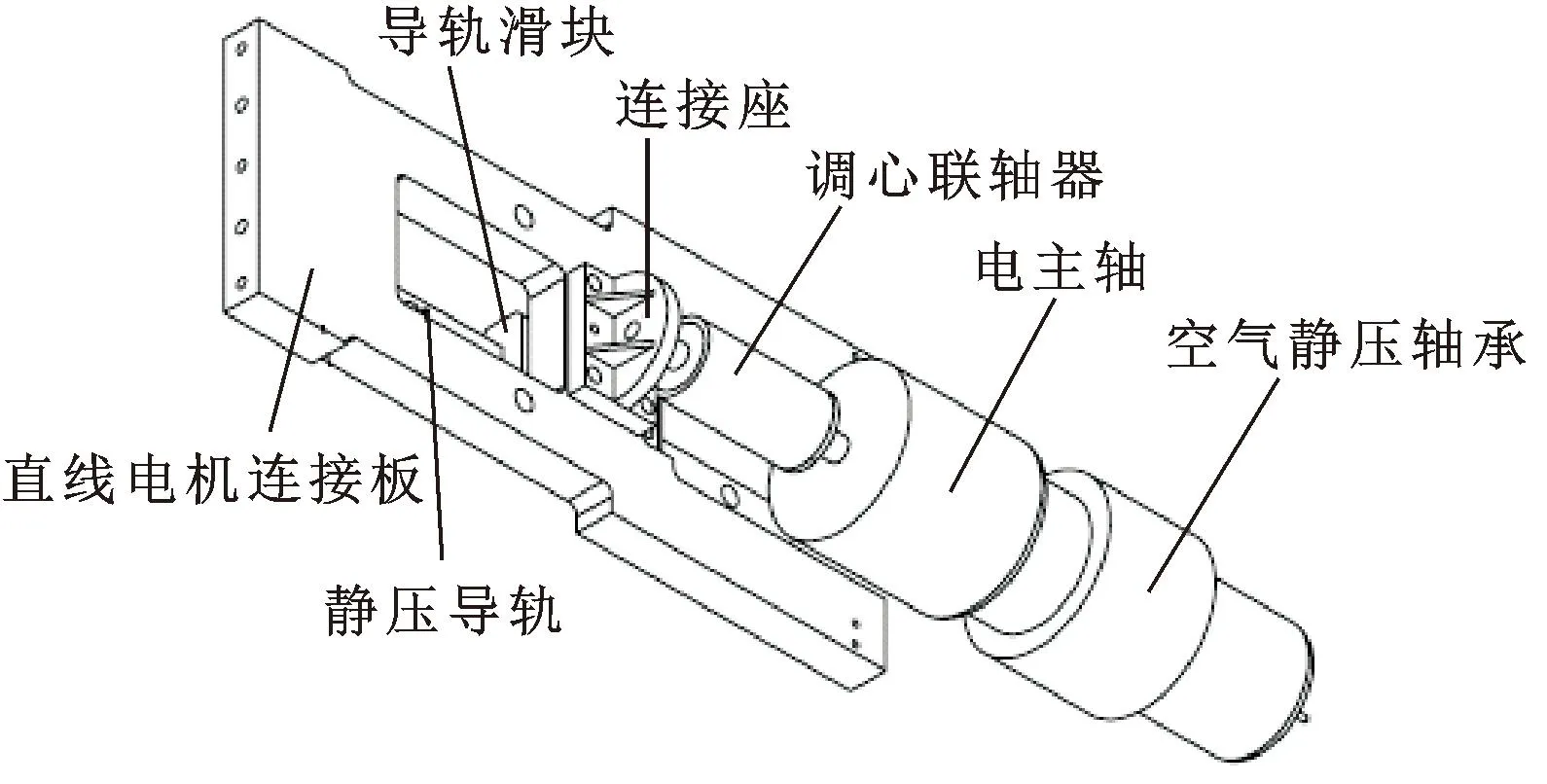
图2 下钻机构主轴系统结构

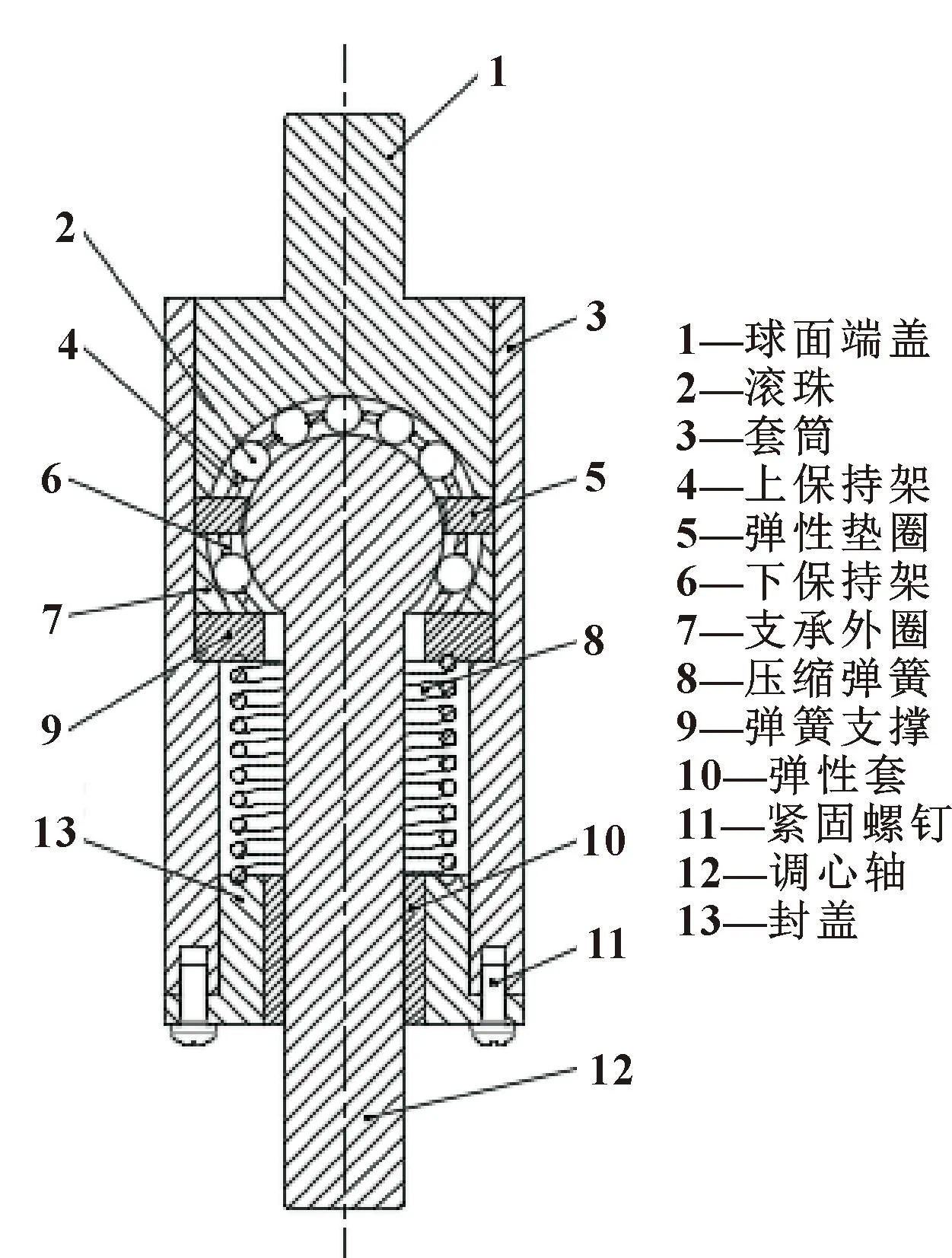
图3 调心联轴器结构

2.2 下钻机构主轴系统模型分析

为方便动力学建模与分析，将下钻机构主轴系统简化为二维模型，如图4所示。对于主轴系统中的调心联轴器，其结构中的调心轴属于细长杆且刚性较差，而调心轴的柔性变形对主轴部分动态特性影响较大，所以在动力学建模过程中其柔性变形不能忽略。将其视为柔性体，其余部分将视为刚体。

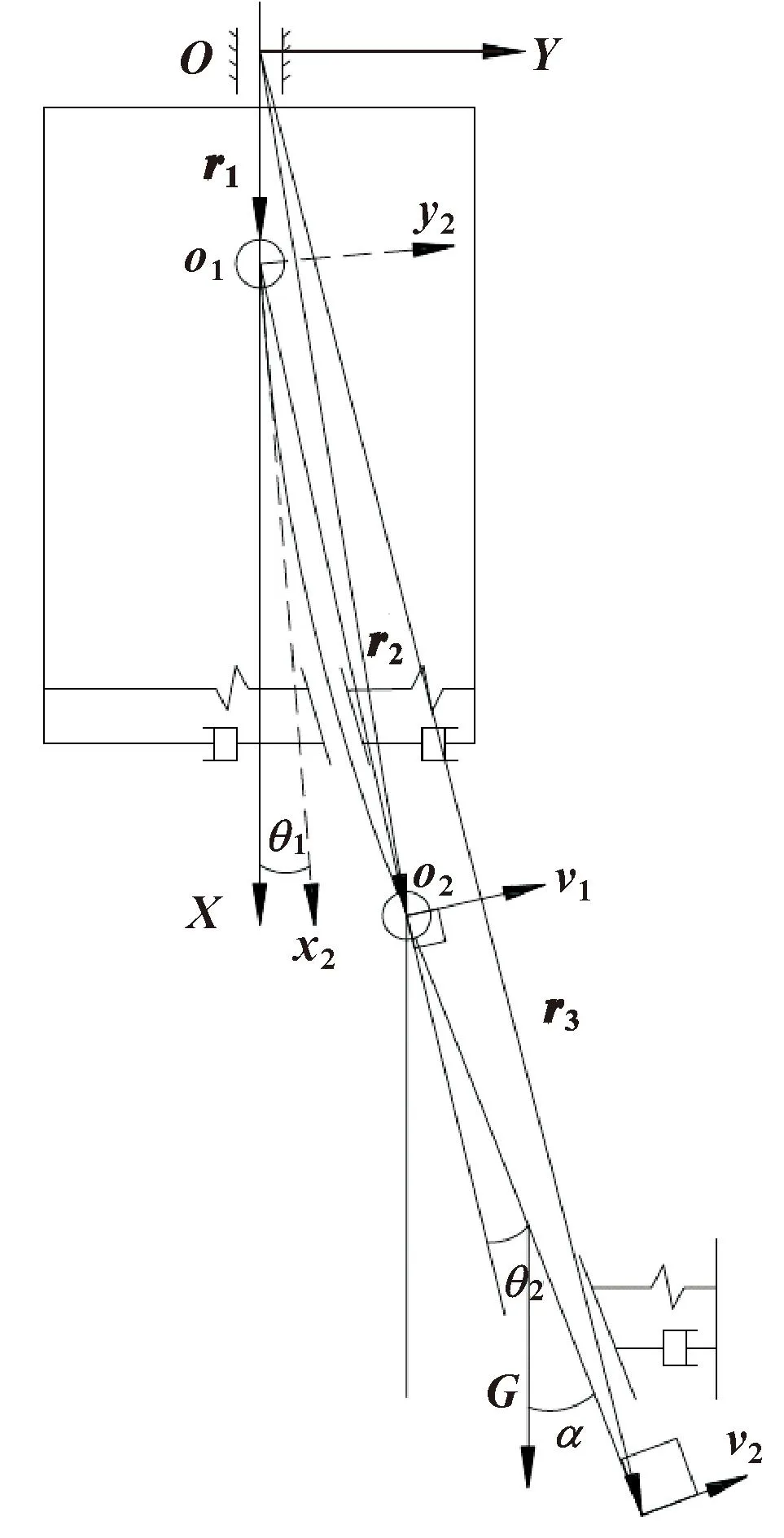
图4 主轴系统刚柔耦合分析模型

调心联轴器中将球面上端盖、保持架、支撑套和外套筒等部分视为整体，该部分和连接座以及电机连接板形成固定联接，直线电机连接板和导轨、滑块形成刚性滑移系统，在滑移系统滑移起始位置建立惯性坐标系O-XY。调心联轴器中调心轴和上端盖为球铰联接，调心轴嵌套在弹性套上，受到其弹性力和阻尼力的影响，将弹性套简化为弹性阻尼系统，其刚度系数和阻尼系数表示为k1和c1。调心轴下端和电主轴相连，电主轴受到空气静压轴承支撑，轴承受弹性力和阻尼力影响，将轴承简化为弹性阻尼系统，刚度系数和阻尼系数表示为k2和c2。调心联轴器上端盖固联部分和连接座以及电机连接板组成的刚性部分视为刚性梁，质量为m1，其长度为l1，滑移系统在驱动力作用下的位移为x；调心轴视为均质同向柔性梁，其长度为l2，线密度为ρ，质量为m2；柔性调心轴和刚性部分之间的夹角为偏差角θ1。调心轴轴端和电主轴轴线夹角为θ2，电主轴由于安装偏差，其轴线与竖直方向形成的夹角为偏差角α，电主轴部分长度为l3，质量为m3；系统重力为G。

2.3 钻孔机构刚柔耦合动力学方程建立

将柔性调心轴视为欧拉-伯努利梁，建立钻孔机构的刚柔耦合动力学方程，在刚性梁端部和柔性梁联接处建立局部坐标系o1-x2y2；位置向量r1为指向刚性梁端部向量，r2为指向柔性调心轴末端o2的向量，r3为指向电主轴轴端的向量。在驱动力作用下调心轴轴端处的柔性位移表示为v。文中只考虑在XY平面内的横向位移。在描述柔性调心轴位移时选择更加符合梁轴柔性弯曲理论的表述方法[23]，向量r1、r2和r3在惯性坐标系内表述如下：

(1)

(2)

(3)

重力向量表示为：GT=[Gcosα0]。

考虑到调心联轴器中调心轴末端弹性变形引起的微小柔性位移v，系统动能T和势能V表示如下：

(4)

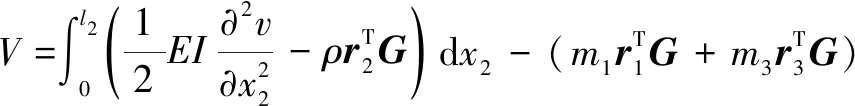
(5)

在钻孔系统动能表达式中柔性调心轴的动能表达式比较复杂，表示如下：

(6)

为充分考虑调心轴的柔性，连续的柔性位移被离散为有限序列，即

(7)

式中：φi(i=1,2…,S)为模态形函数；qi(t)为模态坐标。轴端模态形函数定义为φl，以式(6)为基础，调心轴柔性动态方程是模态坐标变分的系数，得到：

服务特点：I）最全最权威的生物医学数据库，提供在线检索与获取全文服务；II）揭示药物与疾病的关系和药物之间的相互作用；III）更有效检测药物不良事件的文献；IV）提高医学工作者工作效率（提供药物、疾病检索方式）。（提升检索效率与准确性，是其核心服务之一）

(8)

如果考虑N阶模态，则出现N个独立方程。

系统中广义力包括钻孔机构下钻引起的轴向力f以及弹性套和电主轴空气轴承引起的力矩τ1和τ2。

(9)

(10)

推导钻孔机构系统的动力学方程依据如下哈密尔顿原理：

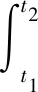
(11)

根据公式(1)—(11)推导整个系统的动力学表达式，由于广义坐标变分的任意性，根据坐标变分δx、δθ1、δθ2系数项推导整个系统刚柔耦合动力学方程如下：

(12)

(13)

(14)

3 下钻机构主轴系统的动力学数值分析

钻孔机构下钻完成主要由直线电机驱动，带动直线电机连接板沿导轨方向上下运动实现钻孔。钻孔机构模型各个结构参数如表1所示。由于电主轴转速高，钻头受到的切削力较小，所以钻孔时主轴系统受到的轴向力f也较小，钻孔轴向力的变化不大，平均值大约为5 N，方向竖直向上[3]。

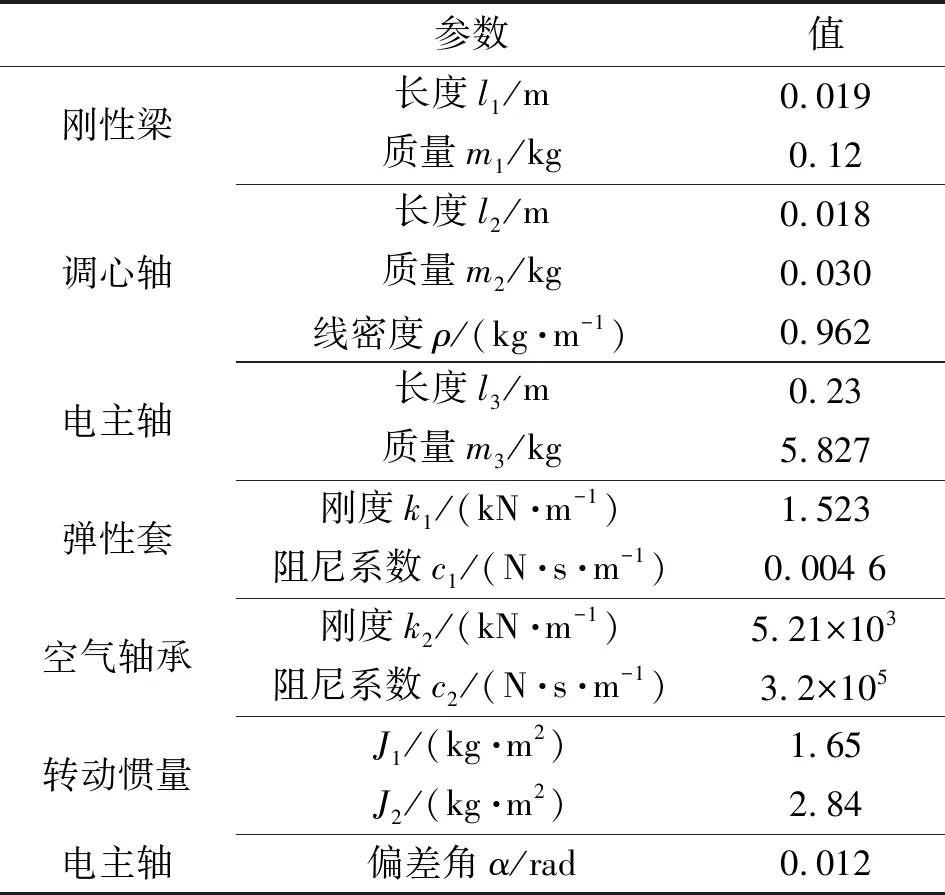
表1 下钻机构主轴系统结构参数

根据钻孔机构在钻孔过程中对直线电机运动的数据监测，得到下钻时Y方向上的位移变化曲线，该曲线作为下钻系统的输入曲线。完成钻孔所需时间为0.6 s，如图5所示。

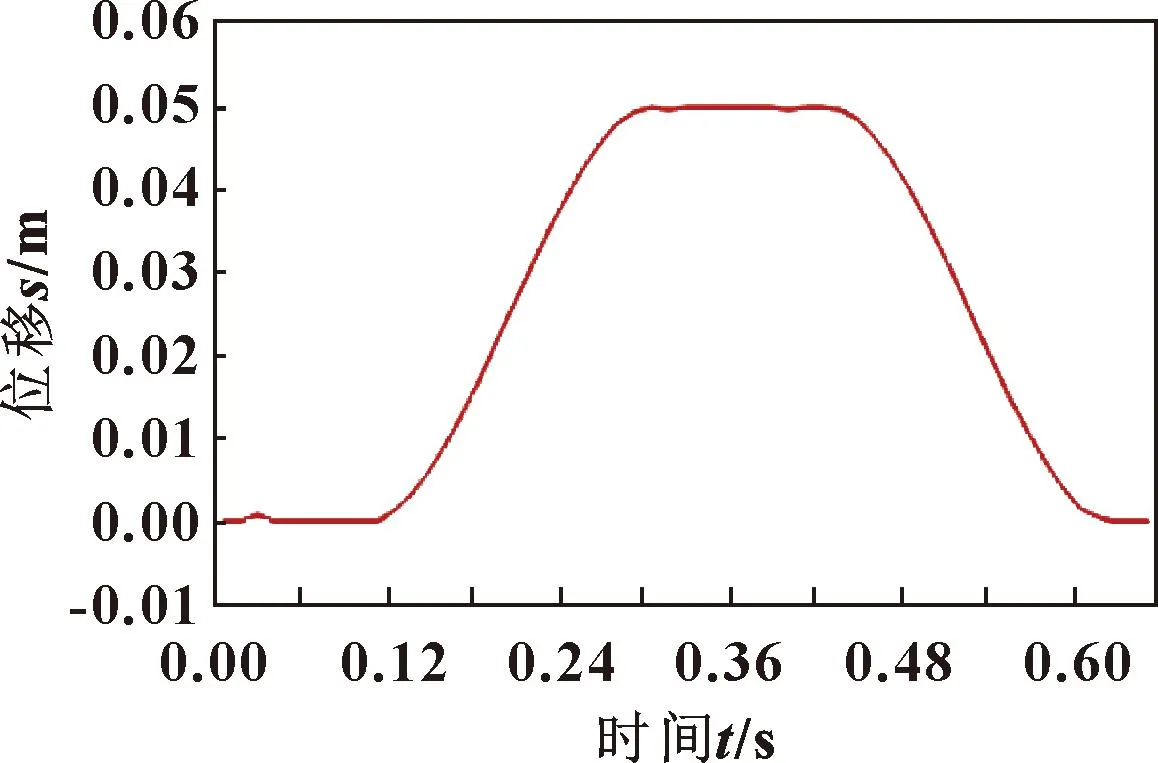
图5 下钻机构输入曲线

考虑到调心轴偏差角和调心轴柔性状态的耦合，动力学方程结构较为复杂。根据下钻机构的外部输入曲线数据，将下钻机构输入曲线数据代入公式进行仿真计算，得出调心轴偏差角θ1和调心轴轴端与电主轴轴线夹角θ2的变化曲线，如图6所示。可知：θ1和θ2的变化规律与下钻机构输入曲线形状大致相似，不同的是角度变化中有振动偏差。角度变化包括大范围刚性运动引起的角度变化和调心轴柔性振动引起的角度振动误差。θ2的刚性运动引起的角度变化量大于θ1的角度变化量，而柔性振动引起的振动误差变化使得θ1的柔性误差略大于θ2。

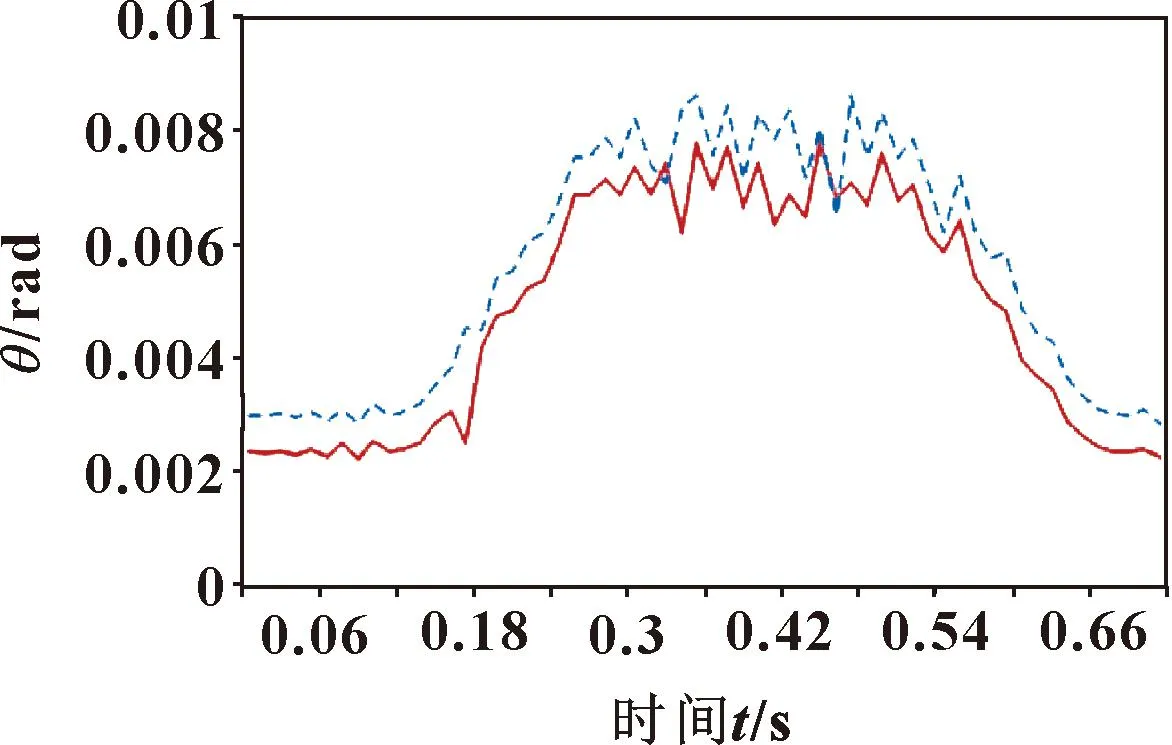
图6 下钻过程中角位移变化

由于调心轴的柔性振动引起轴端微小位移偏差，其振动如图7所示。在钻孔过程中，下钻开始阶段柔性振动较小，随着钻孔的深入，其柔性振动越来越大，当PCB板钻孔最深处时，其振动达到最大值，钻头退出时，调心轴振动随之减小。所以在进行多层PCB板钻孔时，由于刚开始振动小，所以上层板精度较高；当加工到底层板时，调心轴振动最大，较大的调心轴振动引起钻头的振动较大，所以底层板孔壁质量较差。

不同调心轴刚度对调心轴轴端与电主轴的夹角θ2有一定的影响，分别取调心轴刚度系数k=1.25 kN/m和k=0.85 kN/m，通过仿真分析得到如图8所示曲线。可知：增大调心轴刚度可以一定程度上减小θ2，主要是因为刚度增加引起调心轴柔性振动减小，从而减小θ2。

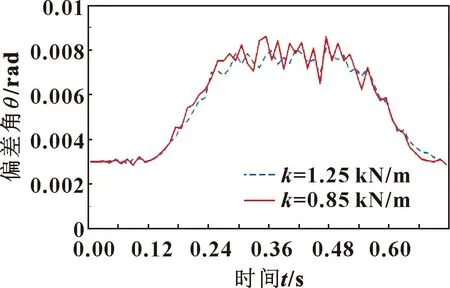
图8 不同调心轴刚度对θ2的影响

图9所示为考虑调心联轴器有无弹性套阻尼情况下偏差角θ2的振动偏差，在有阻尼和无阻尼情况下，θ2大范围的运动基本变化不大，但小范围的角度振动有区别。有阻尼时振动幅值减小，振动减缓。所以通过增加一定的阻尼可以减小θ2的振动幅值和频率，减缓角度振动。

图10所示为电主轴空气轴承不同的阻尼c2对偏差角θ2的影响。空气轴承不同阻尼系数c2=0.8×105N·s/m和c2=3.2×105N·s/m进行对比，在主轴系统开始下钻时，不同阻尼对偏差角θ2的影响效果并不明显，但随着下钻的深入，特别是下钻到底部时，较大的阻尼系数可以明显减小偏差角θ2的偏差值以及振动误差，振动曲线也趋于平缓；当下钻结束钻头退出时，不同阻尼对偏差角θ2的影响不明显。从图10可以看出：增大电主轴阻尼虽然在起钻和结束钻孔时对钻孔精度的影响不大，但对PCB底层板的孔的加工影响明显，可以减小底层板的钻孔偏差，提高钻孔的孔壁质量。

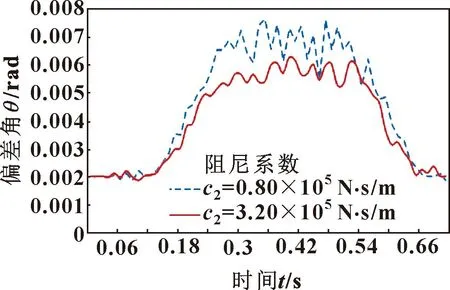
图10 不同空气轴承阻尼对θ2的影响

4 结论

通过对影响PCB钻床下钻机构钻孔精度的因素进行分析，找出了影响加工多层PCB板钻孔偏斜和电主轴产生柔性振动的主要原因，建立了主轴系统的刚柔耦合动力学方程，并进行了分析，得到如下结论：

(1)调心联轴器中的调心轴偏差与电主轴的安装偏差形成的偏差角对钻孔有一定影响，通过提高下钻机构主轴系统的安装精度，减小电主轴的位移偏差以及角度偏差，使得偏差角θ1减小，可以提高钻孔孔位精度。

(2)钻孔过程中，随着钻孔的深入，电主轴部分在水平方向上的柔性振动加剧，导致钻头钻孔的振动也加剧，使得PCB底层板孔径发生变化以及引起孔壁质量下降。

(3)调心轴的柔性振动对主轴系统的钻孔稳定性有一定影响，适当增大调心轴刚度可以减小主轴系统在下钻运动过程中的稳定性，减小偏差角θ2的振动偏差。

(4)电主轴空气轴承的阻尼对柔性振动有一定的抑制作用，增加空气轴承阻尼可以减小偏差角θ2的偏差值以及电主轴部分的柔性振动幅值，达到减小PCB底层板的孔位加工误差和提高孔壁质量的目的。