非均匀预紧力对主轴系统回转性能的影响研究
宁运鹏,袁峰,刘吉文,秦东晨
(郑州大学机械与动力工程学院,河南郑州 450001)
0 前言
现代主轴为了适应更大的加工范围,必须具有较高的刚度和回转精度。大量的研究表明[1]:影响主轴系统刚度的因素有很多,比如材料、轴承刚度、轴承跨距、轴长度等。其中预紧力在提高主轴系统刚度方面起到了重要作用,合适的预紧力是主轴优良动态性能的保证。为了使高速主轴系统获得最佳性能,在其制造和装配阶段,需要调整轴承预紧力。
按不同的轴向预紧措施[2],轴承预紧可以分为定位预紧和定压预紧。但是无论是相应的刚性预紧或弹性预紧,对轴承外圈的轴向预紧都默认采取均匀施加载荷的方式。由于机床加工过程中的复杂情况,轴承与其他零件的接触载荷总是不可避免地出现非均匀的接触载荷。
许多研究中提到过零件之间非均匀预紧的情况[3-7],如主轴轴承装配过程中,串联轴承之间装配的轴套,由于加工误差或者长期的径向载荷导致其端面并不是理想状态下完全垂直于轴线,并因此使零件之间的加载出现不均匀的情况[3,8]。由于高速运动引起的摩擦生热以及热量分布不均匀,导致轴承零件内不同程度的热膨胀,同样可以引起轴承加载的不均匀[4]。进行金属切削加工时会给整个主轴系统带来径向载荷,同时产生一定的扭矩,除了导致轴承的径向偏转和角度偏转,还会使得零件之间产生非均匀加载情况[9]。
上述现象产生的结果会影响主轴系统的稳定性以及轴端的回转性能[10],也会影响加工工具的寿命和加工效率,而主轴轴心的回转轨迹是高精度主轴重要的性能指标,它将会直接影响到加工零件的几何误差和表面质量。
本文作者主要研究外载荷作用下、不同的非均匀预紧载荷对主轴系统的轴端轴心轨迹的影响。此研究主要在角接触球轴承-主轴系统试验台上进行预紧力试验,试验台具有可控预紧力、监测轴端轴心轨迹、施加不同转速、施加径向载荷等功能,能够模拟不同的主轴工况,在轴承外圈施加均匀预紧载荷与非均匀预紧载荷,将实时监测的轴心轨迹收集到计算机中处理并分析。为了更方便地评定不同工况下的轴心轨迹,使用评定圆度误差的最小二乘圆法对轴心轨迹进行评定。为了验证非均匀预紧载荷工况对主轴轴心轨迹产生的影响,设计不同的转速、均匀预紧力、非均匀预紧力试验方案进行试验验证。
1 试验台配置及试验设计
1.1 试验台配置
此次研究所使用的试验台可以分为主体结构、加载装置、测控系统3个部分。其中试验台主体细节具体如图1所示。

图1 试验台SolidWorks模型
1.1.1 试验台加载装置
为了模拟切削机床的实际工况,通过在主轴轴端施加径向载荷来等效机床在切削时产生的切削力。具体的加载装置如图2(a)所示。
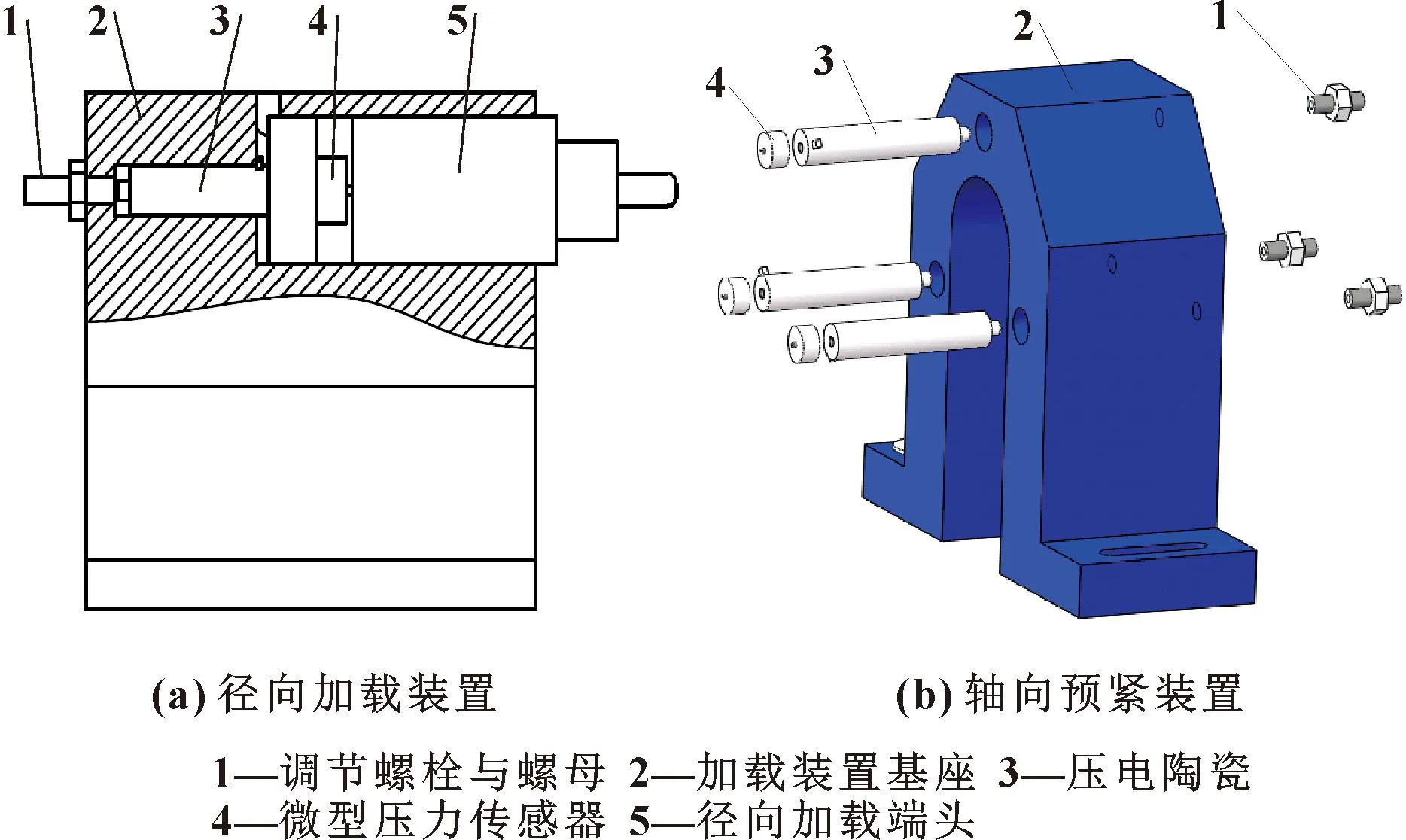
图2 加载装置
在2个轴承座之间固定放置轴承外圈预紧的加载装置,在轴承外圈的位置均匀放置3个预紧装置,由此在施加均匀预载荷的前提下可以施加非均匀预紧,如图2(b)所示。其中施加径向载荷和预紧力的装置均采用压电陶瓷材料,其整体由调节螺栓和螺母、压力传感器、径向加载结构、封装型压电陶瓷(型号pst150/40/vs15)、加`载装置支架组成。
1.1.2 测控系统
为了实时监测预紧力与径向力的大小,在每一个施力装置的前端都放置了一个压力传感器,其型号为ZNHM-1,精度为0.01 N,灵敏度为1.0 mV/V。而传感器的另一端连接型号为BSCC-H2的压力显示器。
同样地,为了监测主轴轴端在运转过程中的轴心轨迹,采用电涡流位移传感器对轴端的径向和轴向位移进行非接触式测量,其型号为CWY-DO-20XLT05,量程为1 mm,分辨率为0.1 μm。采用常用的双向测量法安装传感器,即将2个位移传感器安装在被测主轴回转面的径向方向上,安装时要注意传感器之间呈90°夹角,如图3所示。
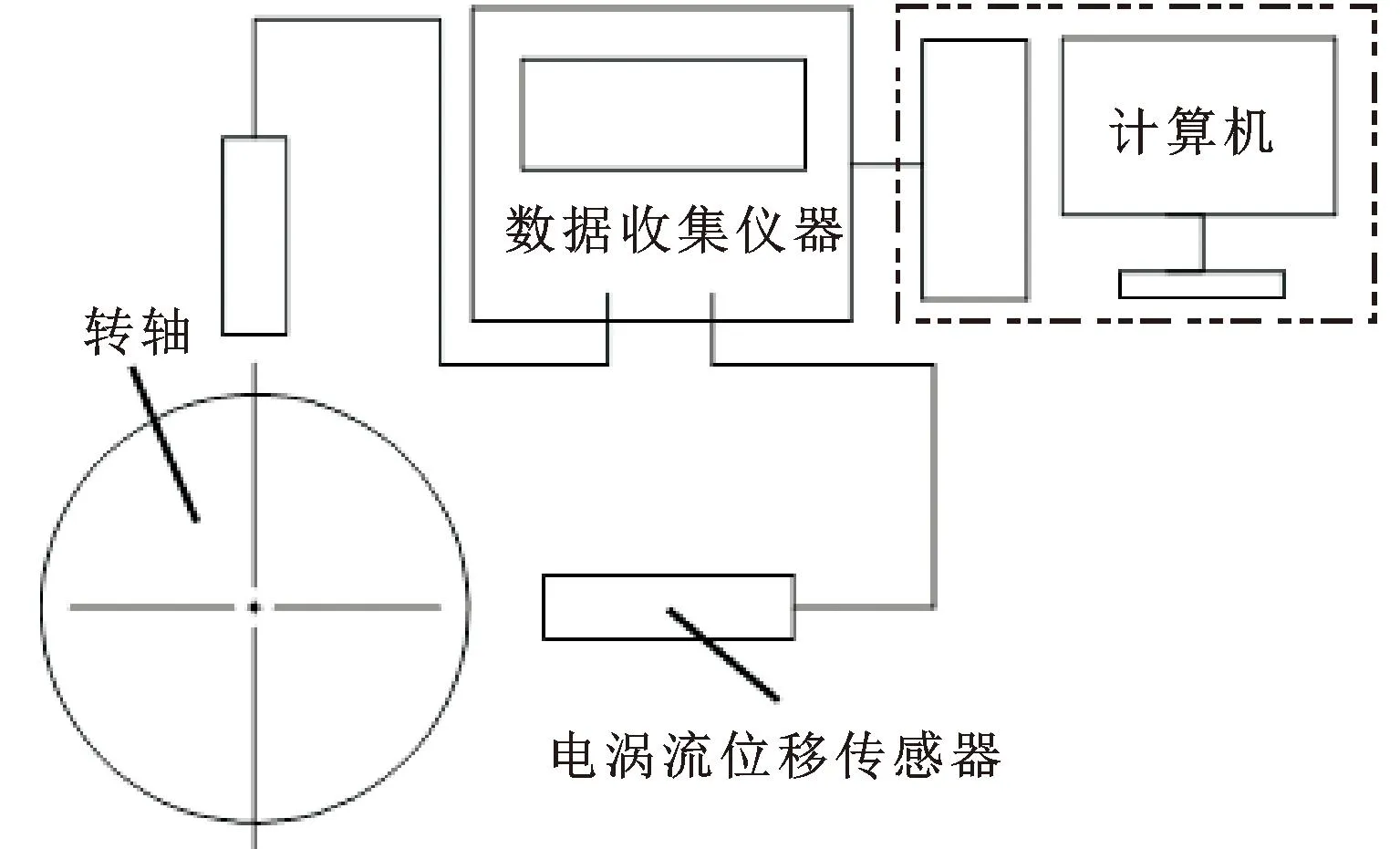
图3 双向测量法
再通过LMS SCM03多通道数据采集仪将数据传到计算机中,通过LMS.test.lab.15A进行处理[11]。
试验台总成的实物如图4所示。

图4 试验台总成
1.2 试验设计
1.2.1 预紧力范围
单个轴承轻预紧力F的经验公式[12]为
F=k1×k2×k3×C
(1)
式中:k1为轴承系列系数,对于7000系列轴取值为0.009;k2为轴承接触角系数,15°时值为1.0,25°时取值为1.5;C为额定动载荷。
此次试验采用的轴承型号为7006C,初始接触角为15°,额定动载荷为19.8 kN,所以由式(1)可以得出轴承的轻预紧力为178.2 N,轻、中、重3个等级下的预紧力比例为1∶2∶4,可以得出不同转速阶段的预紧力分别为178.5、356.4、712.8 N。由此根据试验台的3个施力点确定轴承预紧力的常用预紧范围为300~600 N。
1.2.2 预紧方案
试验台内部共有4个7006C轴承,在支撑基座处均有2个轴承串联布置,而2个基座之间的轴承采用背对背的形式布置。具体信息如图5所示。
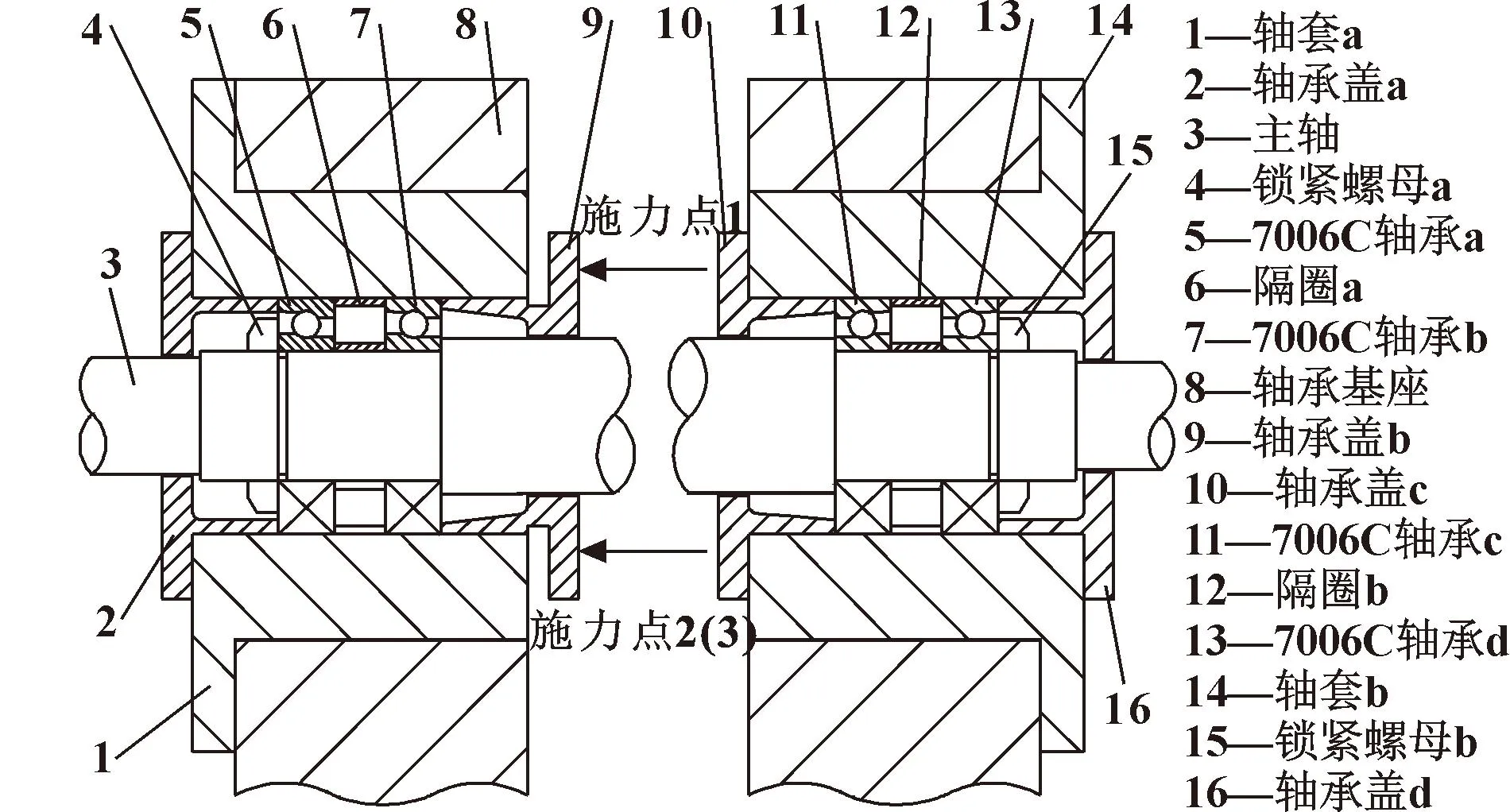
图5 试验台轴承布置形式
而承受可控预紧的轴承有3个施力点,且在轴承外圈均匀分布,如图6所示。
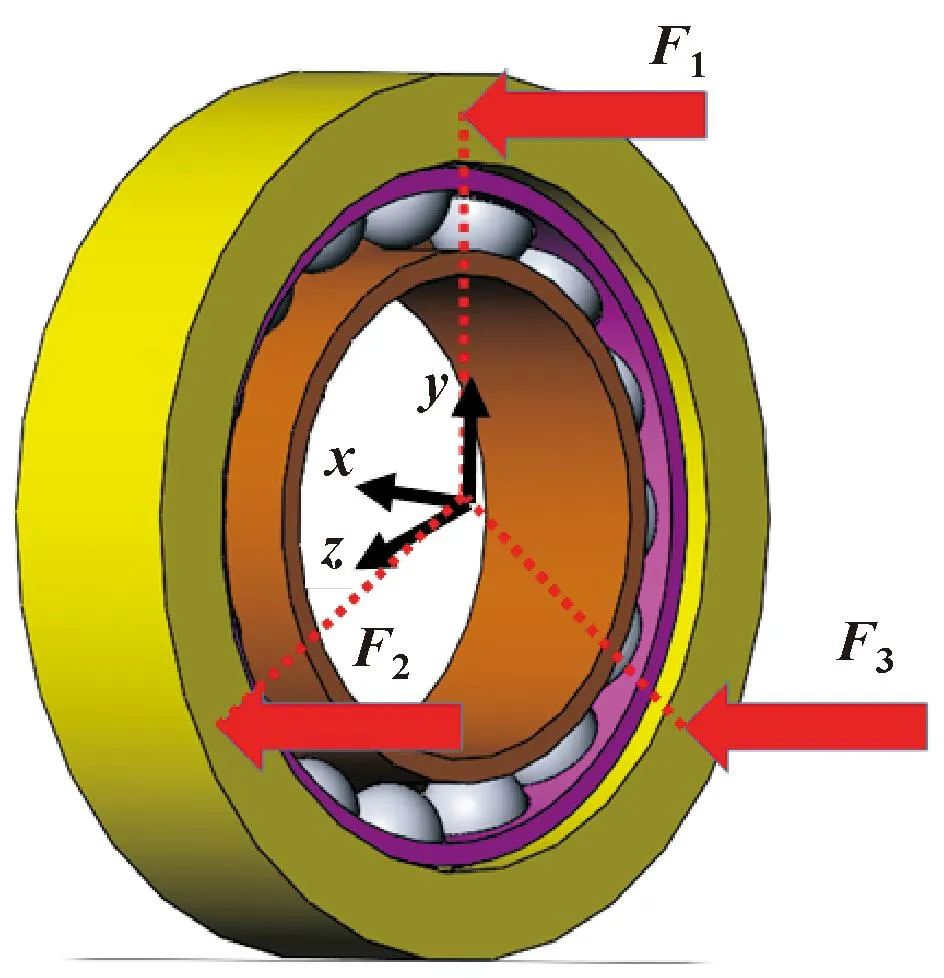
图6 轴承施力点分布
在主轴空载的条件下,当非均匀载荷作用在轴承上的加载点1和点2或点3时,理论情况下,其对轴承的载荷分布的影响相似,只是方向相反。但是由于试验台的装配误差、零件的制造误差、重力的一系列因素在一定程度上对主轴轴端的轴心轨迹产生影响,3个不同的施力点进行非均匀预紧也会产生不一样的效果。所以在空载情况下,也需要对3个施力点施加非均匀预紧,如表1—3所示。
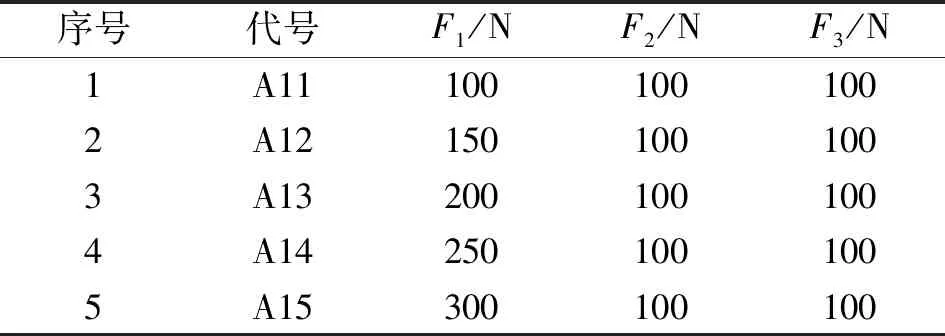
表1 空载下的非均匀预紧A1
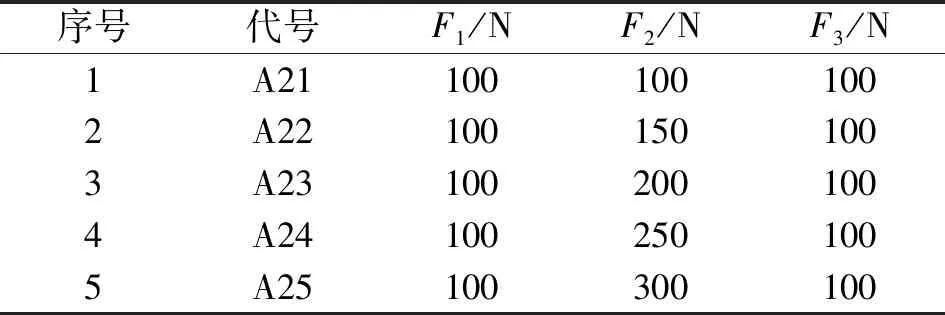
表2 空载下的非均匀预紧A2

表3 空载下的非均匀预紧A3
而在模拟工况的径向载荷下,由于径向载荷导致的非均匀载荷分布与3个施力点没有理论上的对称,所以不同施力点产生的非均匀预紧同样会产生不同的情况,需要考虑在不同的施力点施加非均匀载荷对主轴回转精度的影响。
由上述公式确定预紧范围大致在178.2~712.8 N之间,参考相关文献[2],主动施加非均匀预紧时,会在轴承和主轴中产生扭矩。在不同的施力点进行非均匀预紧时,为保证相同的扭矩,选取一个施力点逐渐增大,而其余2个施力点保持相同的预紧力不变。为方便数据处理,分别选择每个施力点施加100、150、200、250、300 N预紧载荷,而其他的施力点则保持100 N不变,具体的试验工况如表4—6所示。

表4 径向载荷100 N下的非均匀预紧B1
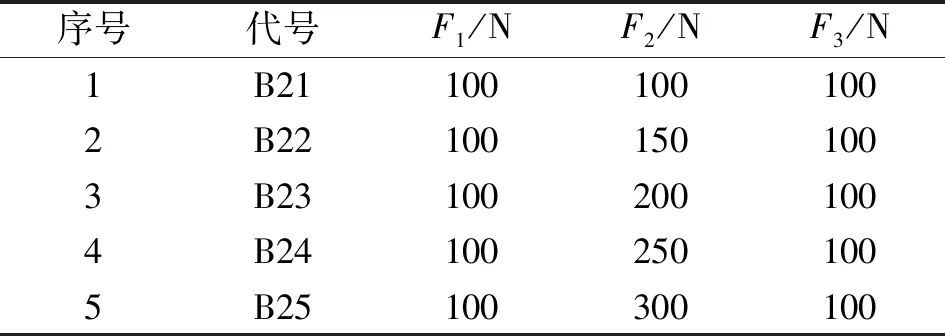
表5 径向载荷100 N下的非均匀预紧B2
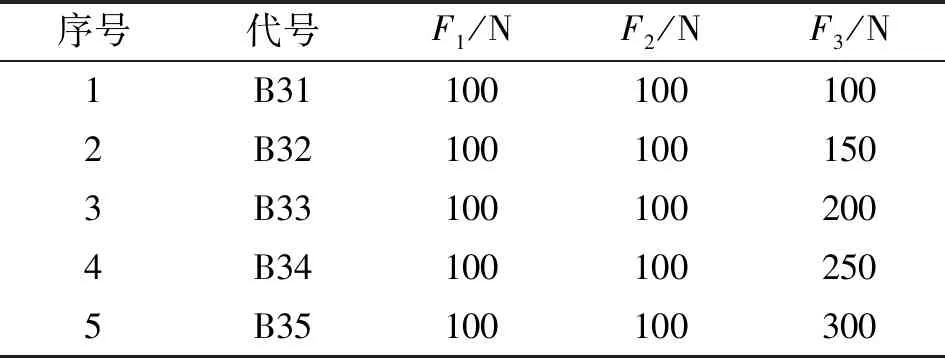
表6 径向载荷100 N下的非均匀预紧B3
2 试验结果处理
先在300 N均匀预紧且空载的情况下以1 200 r/min的转速运行试验台,通过电涡流位移传感器收集数据,并使用LMS.test.lab.15A中的Signature Testing模块绘制轴心轨迹,如图7所示。

图7 轴心轨迹
2.1 最小二乘圆法
最小二乘圆法(Least-Squares Circle,LSC)得到的是个理想的圆,它使从实际被测轮廓上各点到该圆周的距离的平方和为最小[13]。为了更好地评定不同工况下的轴心轨迹,采取评定圆度误差的最小二乘圆法来评定轴心轨迹。并将最小二乘圆的半径作为轴心轨迹的特征值。
圆的最小二乘拟合过程就是利用实际轮廓的测得值,确定圆心位置和圆半径的过程[14]。
图8中点O表示双向测量法中2个传感器垂直布置下的回转中心,ri表示轴心轨迹某一点到点O的距离,最小二乘圆的圆心为Olms,其位置坐标为(x0,y0),最小二乘圆的半径为rlms。
机器人操作系统(ROS)是一套用于机器人设计与控制的操作系统。ROS不仅提供了丰富的操作功能,如底层设备控制、进程间的消息传递,还整合了主流的库函数,如OpenGL、OpenCV,并且拥有很多传感器的驱动程序,包括Kinect、激光测距仪等[1]。该系统可概括为以下2个特点:

图8 最小二乘圆法
最小二乘圆的计算公式[15]为
(2)
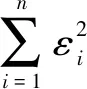
2.2 牛顿迭代法
采用较为广泛的牛顿迭代法来求解最小二乘圆。为便于计算,设:
(3)
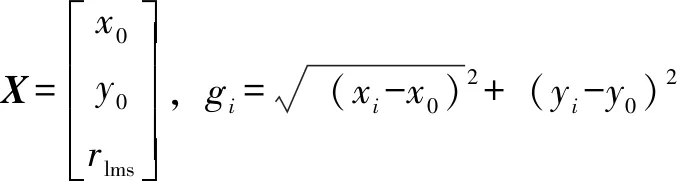
对f(x0,y0,rlms)求偏导获取最小值:
(4)
对f(x)求导得到Jacobi矩阵:
(5)
(6)
将平均值设置为迭代初值:
(7)
编写最小二乘圆法的MATLAB程序,并将收集到的轴心轨迹数据导入MATLAB中,运行之后得到的图形如图9所示。
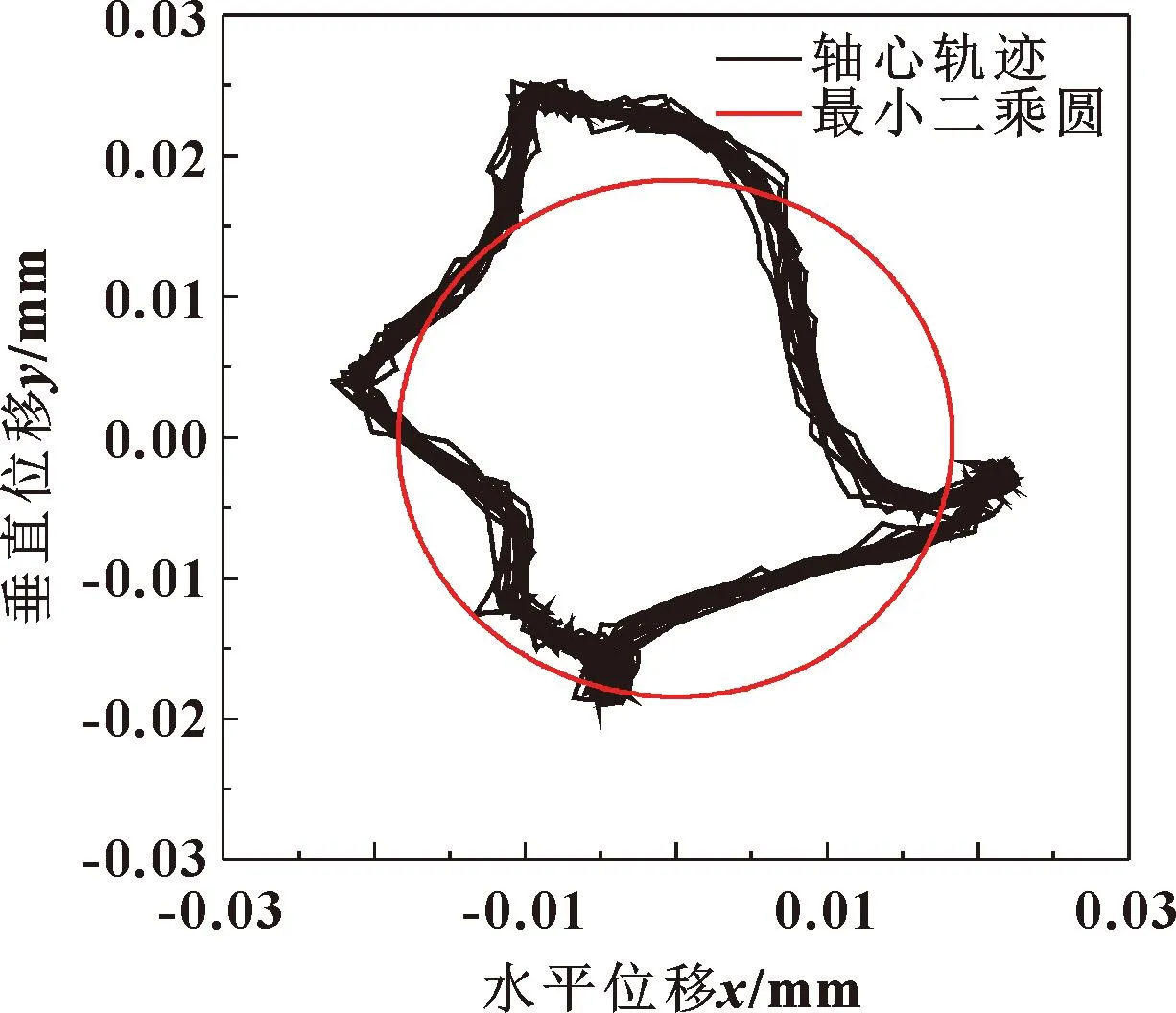
图9 轴心轨迹的最小二乘圆
3 试验结果分析
3.1 空载下的非均匀预紧
在主轴空载的工况下,施加表1—3中的预紧方式,为了消除单一转速下带来的偶然性,分别在1 200、1 500、2 000、2 500、3 000、3 500 r/min转速下进行轴承预紧试验。其轴心轨迹的最小二乘圆半径r在不同非均匀预紧和转速下的变化趋势如图10所示。可以看出:随着转速的增大,轴心轨迹的半径也增大,原因是离心力的增大使得轴承的径向间隙增大;同时,即使在不同的转速下,轴心轨迹随非均匀预紧的变化趋势一致,说明非均匀预紧可以改变轴心轨迹的半径。由此证明了当试验台零件之间存在非均匀加载情况时,合适的非均匀预紧可以在一定程度上改善并提高主轴的回转性能。

图10 主轴空载下的非均匀预紧
由图10可知:施力点1、2处随着非均匀加载的增大,轴心轨迹的最小二乘圆半径都是先增大后降低,最后有上升的趋势。由于轴承盖和轴套自身的制造误差或者与其他零件之间的装配误差,出现了图11所示的间隙A、B、C。而产生非均匀预紧的施力点1处于图11中无间隙的位置。
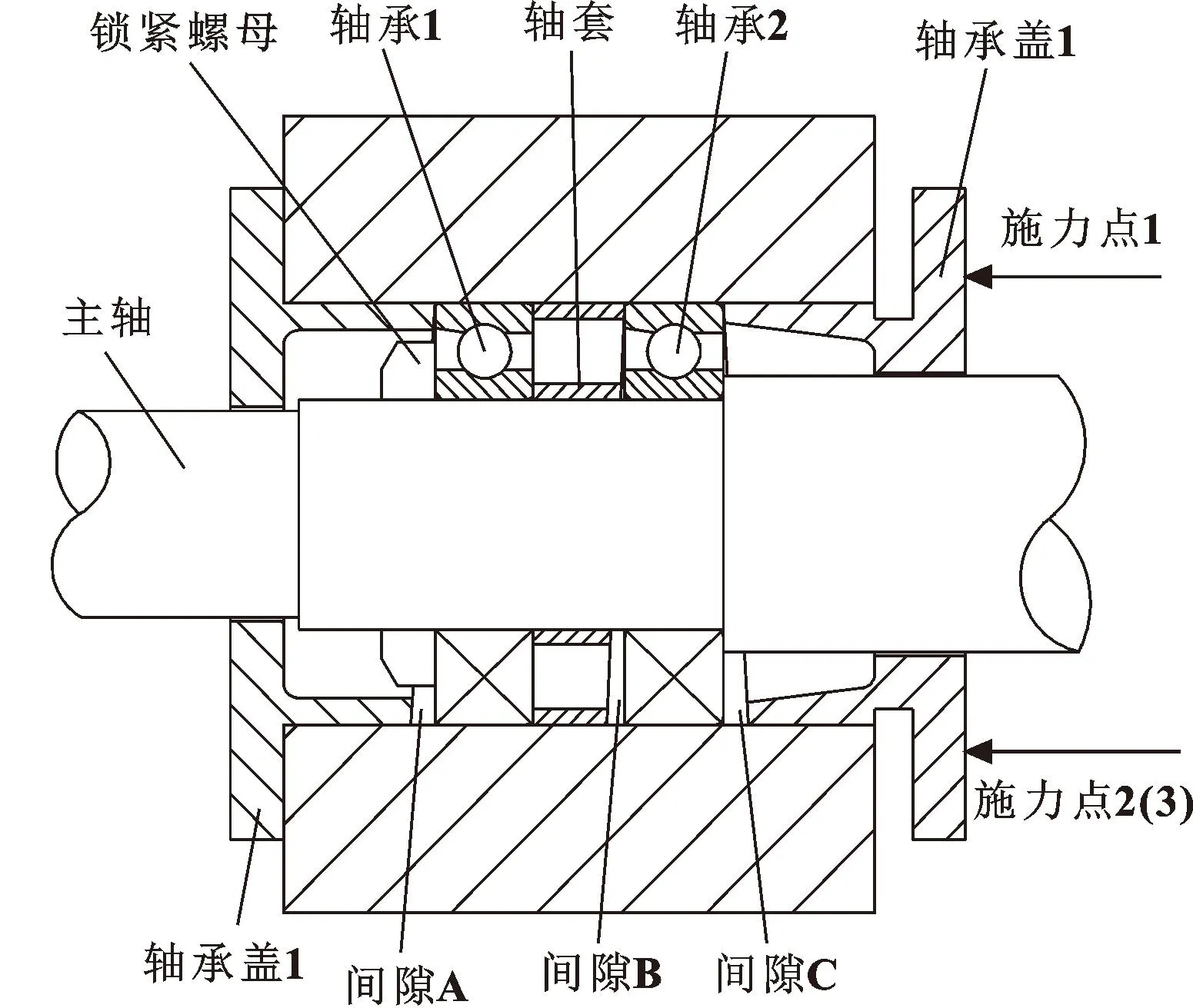
图11 非均匀预紧示意
随着非均匀的持续增大,由图11中施力点的位置可知,此时的非均匀预紧不会减小,且间隙A、B、C反而增大,导致图10(a)(b)中轴心轨迹半径先增大。另一方面,随着施力点继续增力,预紧力整体会增大并减小间隙A、B、C,如图10(a)中A14处和图10(b)中A23处轴心轨迹半径降至最低。之后在施力点1继续增大预紧力,非均匀预紧趋势开始提高,间隙A、B、C开始增大,同时轴心轨迹半径开始增大。
由图10(c)可以看到:在施力点3处,轴心轨迹半径在非均匀的加载下并没有产生较大的变化,只是在A33处减小,后随着预紧载荷增大又回升,与原来均匀预紧载荷相近并趋于平稳。这说明在施力点3处有零件装配误差或制造误差等引起的非均匀载荷的影响。
随着非均匀预紧的增大,逐渐弥补了零件之间的间隙A、B、C,在A33处使轴心轨迹半径达到最小;随着非均匀预紧趋势的增大,非均匀受载现象开始加剧,其他装配位置出现新的间隙并产生新的非均匀受载现象。但由于其他零件的刚度,继续增大并不会再加剧非均匀情况,所以开始趋于稳定。
对比图10(c)中不同转速下的轴心轨迹半径曲线可以发现,在低速阶段由于离心力较小,对轴心轨迹影响不大,轴心轨迹半径出现更加明显的先减小后增大现象;但随着转速提高,离心力增大,轴心轨迹的半径变化曲线相比低速阶段更加平稳,这说明较高的转速可以减弱非均匀预紧带来的影响。
在空载的主轴1 200 r/min转速下,不同非均匀预紧形式产生不同的最小轴心轨迹半径,表7中具体显示了其相对于均匀预紧下轴心轨迹半径的变化。

表7 1 200 r/min下最小轴心轨迹半径相对变化(非均匀预紧A1-A3)
通过图10可以直观地看出:对于此试验台,在主轴低速空载转动下,宜采用A3的预紧形式。合适的非均匀预紧分布A33可以最大程度降低轴心轨迹回转半径,提高主轴的回转精度。
3.2 径向加载下的非均匀预紧
同样地,应用表4—6的预紧工况后,进行1 200、1 500、2 000、2 500、3 000、3 500 r/min转速下的非均匀预紧试验,其轴端轴心轨迹的最小二乘圆半径在不同非均匀预紧和转速下的变化趋势如图12所示。
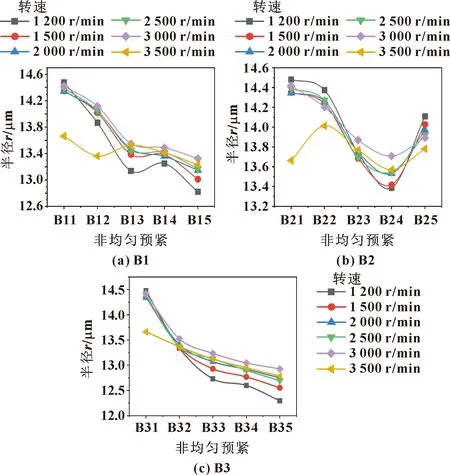
图12 径向载荷100 N下的非均匀预紧
分析图12并与空载工况下的图10对比发现:径向载荷下的轴心轨迹半径普遍小于空载工况下的,径向载荷会增大轴承的角间隙,产生非均匀加载状况,所以随着预紧力的增大,一定程度上会减小轴承的角度偏转,减小轴心轨迹半径。并且在径向载荷下时,转速的变化对轴心轨迹半径产生的影响开始变小,这是因为一定的载荷减小了主轴轴端的径向跳动,提高了轴承径向刚度。
由图12(b)可以看出:随着非均匀预紧的增大,在B24处半径降至最低,之后开始增大,这是由于在施力点2的B24之前增大预紧力,它与其他2个施力点的预紧合力改善了轴承角偏转,减小了轴心轨迹半径。但随着非均匀的力继续增大,预紧力改善轴承角偏转的作用逐渐减小,而非均匀预紧的加剧开始使轴心轨迹半径增大。
在图12(a)(c)中,随着2种预紧工况下非均匀趋势的增大,相应的轴心轨迹半径逐渐减小。
其中施力点3导致的非均匀预紧减小的幅度更大,这同样验证了空载试验下,施力点3处的非均匀预紧可以更好地提高回转性能。
在径向载荷100 N的主轴1 200 r/min转速下,由图12可以得到3个不同形式的非均匀预紧产生的最小轴心轨迹半径。表8为同样条件下其相对于均匀预紧下轴心轨迹半径的变化。

表8 1 200 r/min下最小轴心轨迹半径相对变化(非均匀预紧B1-B3)
对比表8、7可以发现:处于径向载荷下的主轴,经过相同的非均匀预紧所减小的轴心轨迹半径,其相对变化量普遍高于空载主轴下的轴心轨迹半径。这表明径向载荷能够加剧轴承零件之间接触载荷的非均匀分布情况,而施加合适的非均匀预紧(如B3预紧形式下的B35)能够很大程度上减小径向加载带来的影响,提高主轴在径向加工情况下的回转性能。
4 结论
文中主要针对角接触球轴承-主轴系统的非均匀预紧问题进行了试验,运用了轴承-主轴试验台的调速和测控系统收集轴心轨迹数据,使用最小二乘圆法对轴心轨迹进行评定,研究了不同转速下以及不同工况下非均匀预紧对主轴回转性能的影响,主要得出以下结论:
(1)在轴心轨迹半径的变化曲线中有一个共同点,即某一阶段曲线下降之后会有一定程度的回升。这个现象揭示了随着非均匀预紧的增大,整体的预紧合力也会增大,导致即使在预紧非均匀的情况下轴心轨迹半径减小;而非均匀预紧本身产生的弯矩又导致轴心轨迹半径增大,有可能发生2种现象相互抵消的情况。所以在应用非均匀预紧时,需要根据实际情况调整轴承预紧力的非均匀程度,以保持主轴的最佳回转性能。
(2)综合分析试验台主轴空载情况下轴心轨迹半径的变化曲线,在轴承外圈合适的施力点进行非均匀预紧能够降低轴心轨迹半径,提高主轴的回转性能;同样在径向载荷导致轴承预紧非均匀的情况下,可以通过在轴承外圈施加相应的非均匀预紧来改善。

