基于多目标优化的高速超车轨迹规划
刘 刚 ,张 泽,范 群 ,任宏斌,杨 旭
(1.沈阳航空航天大学 机电工程学院,辽宁 沈阳 110136;2.北京理工大学 机械与车辆学院,北京 100081; 3.辽宁陆平机器股份有限公司,辽宁 铁岭 112001)
0 引 言
超车是指后方车辆为寻求更大驾驶空间和行驶速度而超越前车的驾驶行为[1]。在智能驾驶中,规划超车的轨迹不仅需要考虑周围的驾驶环境是否符合超车条件,还需要根据安全与舒适的需求,规划合理的超车轨迹[2]。
为规划出符合安全舒适需求的高速超车轨迹,牛国臣等[3]提出舒适性约束的双五次多项式规划算法,有效提升了规划过程中的舒适性与安全性,但中转位置较难选取;陈鹏宇等[4]对于静止的障碍物提出基于五次贝塞尔曲线的局部路径规划方法,可规划出易于跟踪的避障轨迹,但对感知障碍物后的轨迹自动生成并未进研究;郑亮等[5]通过改进A*算法,并利用Floyd算法自动生成距离最短时间最优的轨迹;荆学东等[6]基于图论与几何的方法改进A*算法,在复杂环境中可有效规划路径,但在高速行驶且路径点过多时会效率降低。为了解决超车过程中实时规划的需求,XU Wenda等[7]采用动态规划对障碍车分析并开辟出凸空间,再用二次规划实时求解超车的全局最优路径,但求解的轨迹舒适性不高且对超车条件未深入讨论;陈治莹[8]分析了周围环境对车辆的影响,建立了基于有限状态机的超车模型,为超车轨迹规划做了前置判断。
综上,为了规划出安全、舒适的超车轨迹,笔者在Frenet坐标系下对参考线进行优化并生成合适的可行凸空间,然后在满足安全超车策略的条件下,基于多目标对超车轨迹进行动态规划。
1 基于Frenet坐标系的参考线优化
1.1 Frenet坐标系
超车规划过程中,车辆与道路的相对位置难以表达,且在笛卡尔坐标系下障碍车的边界约束多为非线性约束。为简化超车路径的规划问题,将笛卡尔坐标系下的三维不规则道路转换为Frenet坐标系下的二维问题进行求解, 如图1。
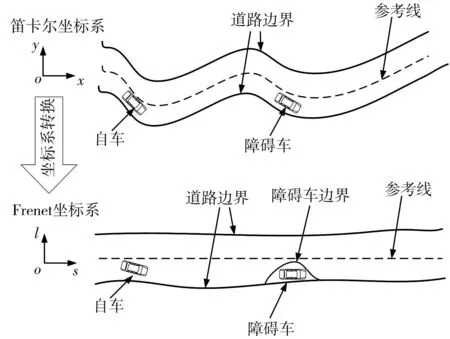
图1 坐标系转换Fig. 1 Schematic diagram of coordinate system conversion
由图1可知:Frenet坐标系下的车辆运动分析更加方便快捷,只需获取车辆的投影点相对于参考线的横向距离l与纵向距离s即可描述车辆运动。
1.2 参考线的选取及优化
在车辆高速行驶过程中,由于参考线存在冗余轨迹信息,导致坐标转换难度加大且自车与障碍车在参考线上的投影点不唯一,从而影响超车轨迹的规划。
为了解决此问题,将参考线轨迹离进行散化处理。同时,考虑实时规划的求解速度,在每个规划周期内,对自车投影点前后各取150 m与30 m参考线上的n个离散点,并建立局部参考线平滑函数Jc。

(1)
式中:q1、q2、q3为对应的权重系数,q1影响轨迹的跟踪精度,q2、q3影响轨迹的平滑性;xi、yi分别为局部参考线上点的横、纵坐标;xi,r、yi,r为参考线上离散点的横、纵坐标。
式(1)中第1项反映局部参考线与原参考线几何形状相似性,第2项反映局部参考线平滑性,第3项反映局部参考点的紧凑情况。
2 超车轨迹规划
2.1 生成可行凸空间
由于轨迹规划问题本质上是优化问题,但由于障碍车的存在,导致超车轨迹规划难度大大增加。为处理复杂驾驶场景,需做出超车预决策来简化轨迹。因此,在Frenet坐标系下生成一个超车预决策的可行凸空间如图2。

图2 生成超车轨迹凸空间Fig. 2 Generating convex spaces for overtaking trajectories
由图2可知:在每个规划周期内,实线部分为可行基准轨迹,考虑规划周期内轨迹的连续性与平顺性,采用五次多项式连接规划周期首尾的基准点(si,li)。在每个规划周期内通过预决策选择轨迹(图2中虚线)后,基于该轨迹得出由道路边界与障碍车边界形成的可行凸空间。即在连续空间离散化后,需要求出离散空间的约束边界。
综上,在每个规划周期内,构建基准轨迹代价函数C,按照最小函数选取合适的预决策轨迹。
(2)

基准轨迹函数C的第1项为可行基准轨迹的平滑函数,第2项为考虑自车与障碍物的距离函数,第3项为反映自车与参考线的距离函数。得到每段基准轨迹的代价函数后,采用Dijkstra算法即可得到与合适的基准轨迹所对应的可行凸空间[9]。
2.2 基于安全性的超车策略
考虑轨迹规划的效率,在求解超车轨迹之前需分析超车的可行性与安全性。国内高速行驶限速60~120 km/h,如果超车加速至100 km/h,事故风险将大大提升[10]。此外,超车最小安全距离[11]为:
(3)
式中:vm为自车车速;tm为反应时间;amax为自车的最大加速度,其大小与路面附着系数和重力加速度有关;h0为安全预留距离,取值随两车车速差变化。
在仅考虑当前车道有障碍车的情况下,由于障碍车存在加减速,当自车车辆传感器感知到障碍车后,综合考虑限速vmax,vmin、两车间距d′、最小安全距离dsafe和自车速度vm与障碍车速度vobs等因素,执行超车策略如图3。
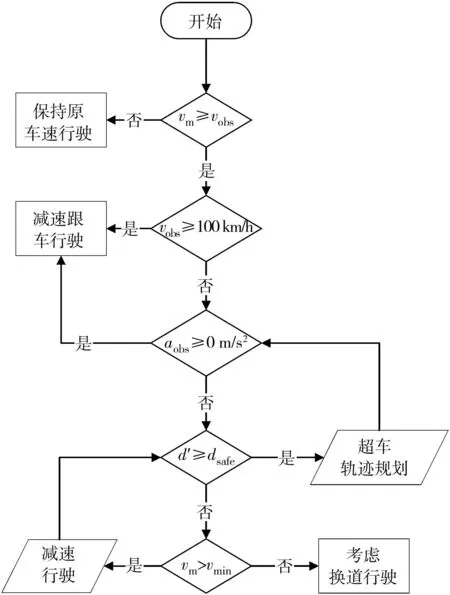
图3 超车策略流程Fig. 3 Overtaking strategy flow chart
根据超车策略,建立基于安全的超车状态机程序。根据不同的高速车辆行驶环境,执行对应的驾驶模式。
2.3 基于多目标的超车轨迹规划
当超车行为执行后,即在可行凸空间中动态求解超车轨迹。考虑超车轨迹的舒适性与平顺性,构建超车轨迹规划目标函数J1为:
(4)
(5)
式中:qref、qd1、qd2、qd3为权重系数,qref影响轨迹跟踪精度,其余3项则影响轨迹的连续性与平顺性;式(5)为约束条件。
J1的第1项反映对参考线的靠拢情况,第2~4项反映超车轨迹的各阶导数,以保证轨迹的平滑性。
基于式(4)规划的超车轨迹,在加速超车时应对加速行为加以约束,同时考虑二次规划求解的超车轨迹有向约束边界靠拢的趋势,会导致超车规划的轨迹换道速度过快和轨迹曲率过大等问题,影响乘坐舒适感与安全性。因此,建立超车舒适边界约束,并设置舒适性优化函数J2(式(7)为约束条件):
(6)
(7)
式中:qv、qa、qk为权重系数,qv与qa影响超车过程的舒适性,qk影响超车过程的安全性;a为车辆加速度;过大的加速度会使乘车舒适度下降,amax=2.8 m/s2[12];k为超车轨迹的曲率,kmax=0.005[13]。
v,a,k计算如式(8):
(8)
式中:kr为参考线的曲率;θ和θr分别为车辆与参考线的航向角。
为了获得舒适、平滑的超车轨迹,在J2中第1项和第2项考虑超车轨迹的舒适性,第3项限制轨迹的曲率为了保证轨迹的平滑。
综上,笔者通过轨迹规划目标函数和舒适性优化函数对高速超车轨迹的平滑性、舒适性和安全性等目标进行了优化。
3 仿真与分析
3.1 仿真平台及参数设计
为验证超车规划的多目标优化效果,建立Prescan和MATLAB/Simulink的联合仿真平台对多目标超车轨迹规划算法进行仿真分析,其超车轨迹规划器框图如图4。

图4 超车轨迹规划器框图Fig. 4 Block diagram of overtaking trajectory planner
在仿真平台中,选用Audi A8 Sedan作为超车车辆和障碍车辆,设置传感器参数模拟激光雷达R- Fans-32和毫米波雷达Delphi ESR各两个分别置于车辆的前后左右,如图5。
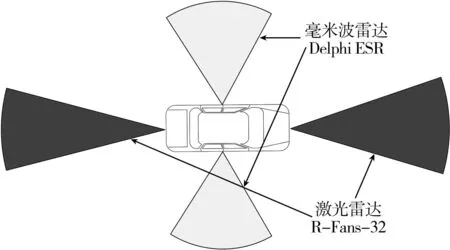
图5 车辆传感器位置信息Fig. 5 Vehicle sensor location information
车辆参数以及超车轨迹规划器的各项约束参数选择如下表1。
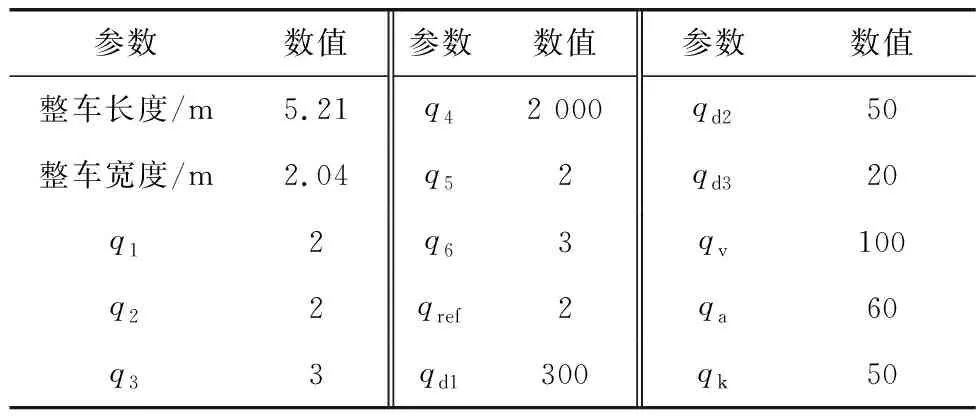
表1 车辆及超车轨迹规划器参数
3.2 仿真结果分析
考虑高速超车工况的多样性,建立仅考虑式(4)的单目标优化和考虑式(4)、式(6)的多目标优化。同时,验证所提出多目标优化的有效性。
3.2.1 场景一(匀速超车)
设置高速超车场景一:自车车速为72 km/h,障碍车车速为54 km/h,两车间距为80 m。匀速超车结果如图6。
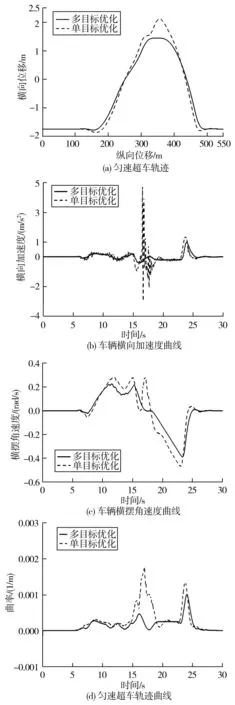
图6 匀速超车结果Fig. 6 Constant speed overtaking results
根据图6(a)匀速超车轨迹可见,在轨迹纵向位移300 m附近,经单目标优化的超车轨迹出现不平滑现象,这是因为超车轨迹通过二次规划有向约束边界靠拢的趋势,但是由于未对超车轨迹的舒适性进行优化。由图6(b)、图6(c)可见,横向加速度和横摆角速度在此时出现了剧烈波动。相反,在多目标优化后,超车轨迹更加平滑,横向加速度和横摆角速度也更加稳定,相较单目标优化有所减小,曲率峰值如图6(d),轨迹的舒适性得到了有效提升。
表2为匀速超车结果分析,根据表2可知,匀速超车情况下,多目标优化可以减小超车轨迹横向位移峰值25.39%,优化超车轨迹横向加速度峰值和标准差分别为79.22%和55.71%,同时横摆角速度峰值减小17.27%;由图6(d)计算得知,曲率峰值减小52.94%。可以看出,在匀速超车场景下,通过多目标优化可以有效提高超车轨迹的规划舒适性和安全性。

表2 匀速超车结果分析
3.2.2 场景二(加速超车)
设置高速超车场景二:自车初始车速为72 km/h,障碍车车速为72 km/h,两车间距为130 m。加速超车结果如图7。
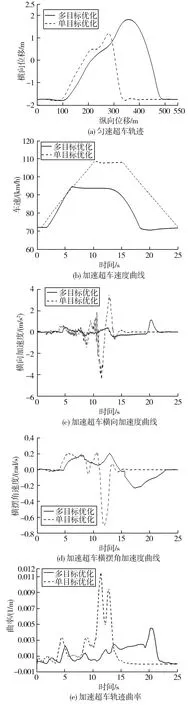
图7 加速超车结果Fig. 7 Acceleration overtaking results
由图7(c)可见,在超车轨迹速度规划过程中,由于单目标优化未对加速行为加以约束,导致在7.5~15.0 s内,横向加速度峰值达到了4.62 m/s2并且出现了明显的波动。由图7(d)、图7(e)可见,在12.5 s附近,基于单目标优化的超车轨迹的横摆角速度和曲率发生不同程度的突变。此外,由图7(a)可见其超车规划的换道时间较短,且速度过快,因此存在较大的安全隐患。相反,基于多目标优化的轨迹规划,通过增大横向位移和减小超车速度保证了超车轨迹的舒适性和安全性。经多目标优化的超车轨迹,其横向加速度、横摆角速度和曲率都有不同程度的改善。
表3为加速超车结果分析,根据表3可知,加速超车情况下,多目标优化减少了横向加速度峰值和标准差分别为74.75%和43.56%,同时优化了车速峰值和标准差分别为12.95%和20.23%,横摆角速度峰值和标准差分别优化了66.98%和30.85%。由图7(e)计算得知,曲率峰值减少60.87%。可见,在加速超车场景下,通过多目标优化可以有效提高规划的超车轨迹的舒适性和安全性。

表3 加速超车结果分析
4 结 论
笔者以超车过程中的轨迹规划为研究对象,建立了同时满足安全性与舒适性的多目标超车轨迹规划算法,通过对超车轨迹规划的仿真结果进行分析得到以下结论:
1)复杂的超车环境在经过安全超车策略分析后,可以避免部分无意义规划,提升轨迹规划的效率。并且提出的超车轨迹规划方法在常见工况下均可有效的规划出实时超车轨迹。
2)相较于单目标规划的超车轨迹,经过多目标优化后的超车轨迹,在匀速超车工况下超车轨迹横向位移峰值减小25.39%,横向加速度峰值和标准差分别减小79.22%和55.71%,横摆角速度峰值减小17.27%,曲率峰值减小52.94%。在加速超车工况下,超车轨迹横向加速度峰值和标准差分别减小74.75%和43.56%,车速峰值和标准差分别减小12.95%和20.23%,横摆角速度峰值和标准差分别减小66.98%和30.85%,曲率峰值减少60.87%。保证了良好的平顺性和安全性,并且横向加速度、横摆角速度和曲率都保持在一个较为舒适的区间。

