基于容器内壁反射能量变化的液位超声检测方法
张跳跳, 贺西平, 刘 昱
(陕西师范大学 物理学与信息技术学院,西安 710119)
超声波具有良好的指向性,在非气体介质中传播距离较远,不易受电磁波、光线、被测液体的颜色等因素影响,因此超声检测被广泛应用于各种领域,如超声指纹[1]、密度检测[2]、缺陷检测[3]、液位检测[4-6]等。在工业生产中,对于具有腐蚀性、易燃易爆、易挥发液体的液位检测,无法采用接触式的检测方法,通常利用超声波在不同介质中的传播特性进行非接触式液位检测,无需对容器进行开孔等操作,并且超声波属于物理波,不具有电磁辐射和电离辐射,不会对检测人员身体造成伤害,超声液位检测具有操作简单、成本较低,对光照和色彩不敏感等优点[7-11]。
基于非接触式[12]超声液位检测,Liu等[13-14]提出利用Lamb波回波信号能量的变化进行液位检测,但需要两个探头,并且需要考虑频厚积对模态的影响,在不同的频厚积下,各模态的面内位移和离面位移占比不同,离面位移占比小的模态不利于判断液面的位置。赵晓阳等搭建了基于介质声阻抗特性超声液位测量系统,但检测精度会受液体纯度的影响[15]。刘赟等[16]从容器底部进行液位检测,但是检测精度易受到沉积物的影响。Wang等[17-18]提出针对密闭容器内的液位检测,其中莫润阳提出小角度斜入射的侧壁式超声液位测量方法,局限是只用于判断液位的有无。现有技术中,侧壁式非接触超声波液位检测的应用更加广泛,但大部分只用于判断探头高度对应范围内液体的有无,对其范围内液位的变化有所忽视。
本文以矩形探头为例,建立了基于活塞辐射声压的声束内壁投影模型,该模型通过计算探头接收到的回波信号能量,进而得到发射探头发射的声束在液罐内侧的投射面积S与罐内液体介质在S中所占面积Sw的比值。利用该比值,可计算出探头高度范围内的液面位置的变化情况。利用有限元进行理论仿真,计算所接收回波信号的能量并得到探头高度范围内能量随液位变化。搭建试验系统验证理论模型及仿真结果的正确性。试验系统搭建完成后,利用示波器采集回波信号,计算对应位置的能量并将计算值代入占比面积表达式中得出相对探头的液面位置。
1 声束内壁投影模型
固定在容器外侧壁收发的矩形探头所发声束线在容器内壁处形成矩形,当液面位于矩形内时,利用占比面积rs=Sw/S和探头接收到的回波信号能量之间的关系,可计算出探头检测范围内的液面位置。图1是矩形声束内壁投影模型,直线AB为液面所在的位置,Δd为矩形声束范围内空气的高度,容器壁厚为L,探头的高为h,宽为a,h′和a′分别为入射波束在容器内壁处形成的矩形阴影区域的长和宽,θx和θy分别为x轴和y轴方向的扩散角。
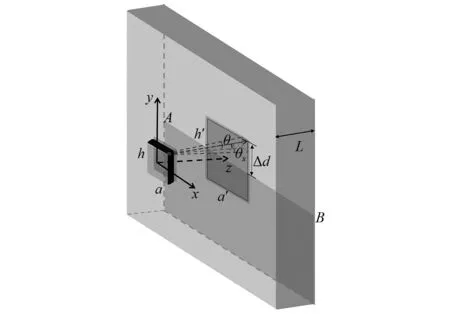
图1 占比面模型图Fig.1 Diagram of the proportion plane model
根据几何关系可得
h′=h+(L-b)tanθy,a′=a+(L-b)tanθx
(1)
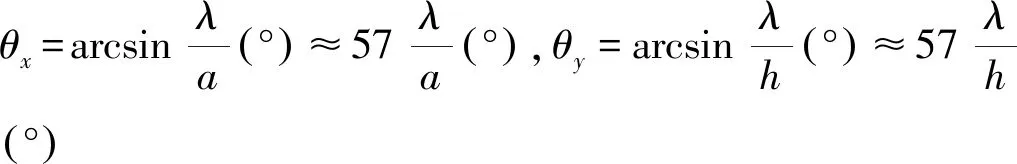
探头发射一列初始声压幅值为p0的超声波,该波束直射到达容器内壁时的平均声压为
(2)
式中:α为容器壁中的衰减系数,可利用长短样品对比法测试得到;Rw为容器内壁处的反射系数,Rw=rsRwl+(1-rs)Rwg。Rwg为固/气界面的反射系数,Rwl为固/液界面的反射系数;s2为投影面积。
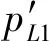
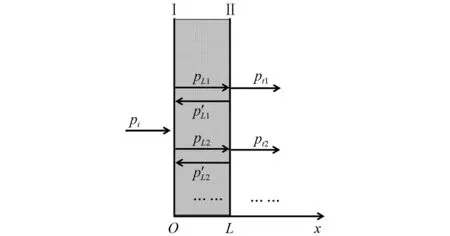
图2 声波传播示意图Fig.2 Schematic diagram of sound wave propagation
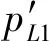
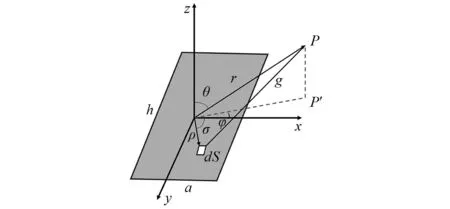
图3 矩形活塞辐射声场示意图Fig.3 Diagram of rectangular piston radiating acoustic field
(3)
式中:k为波数;ω为角频率。
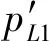
(4)
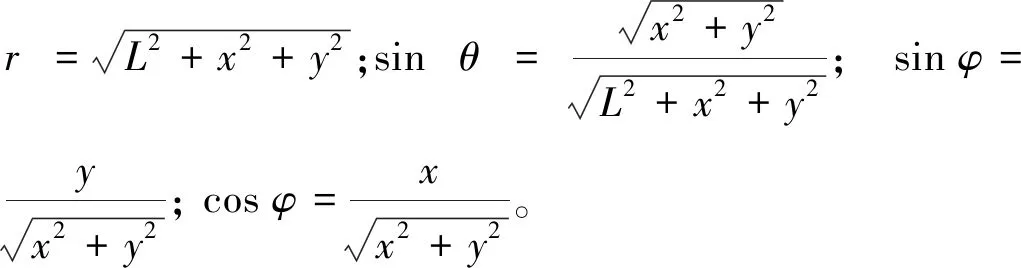
(5)
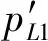
(6)
反射波pL2经界面Ⅱ反射到达界面Ⅰ时的回波声压为
(7)
假设该列经过n次反射的衰减相对总声压为可忽略的微小量,则探头接收到的总的声压为
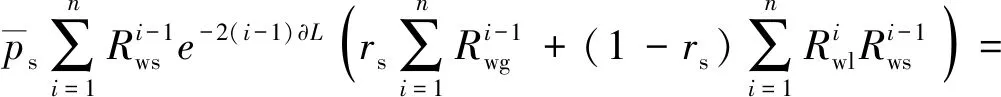
(8)
由(8)式得到声能量为
(9)
式中:W为声能量;ρ0,c0分别为介质密度和声速;s1为探头面积;pe为有效声压;T为取采样时段总声压的时间;pt为采样时段总声压。
(10)
根据式(2)~(10),得到占比面积表达式为
(11)
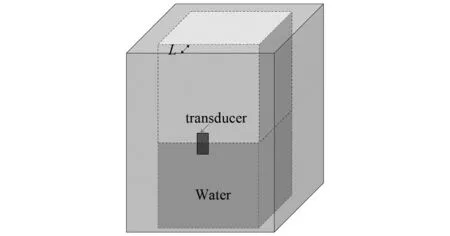
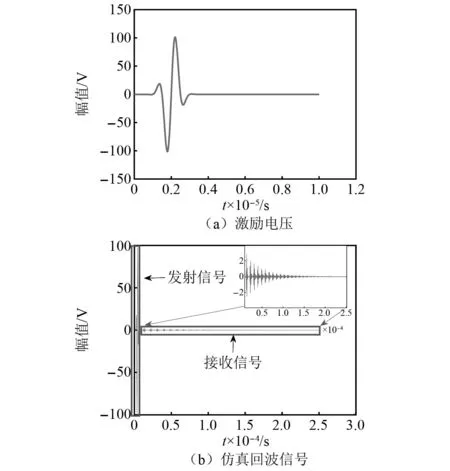
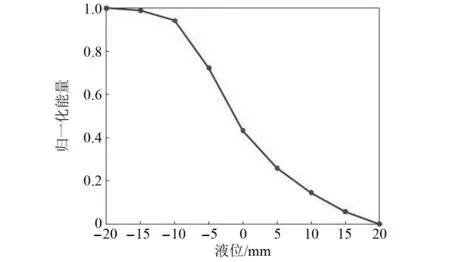
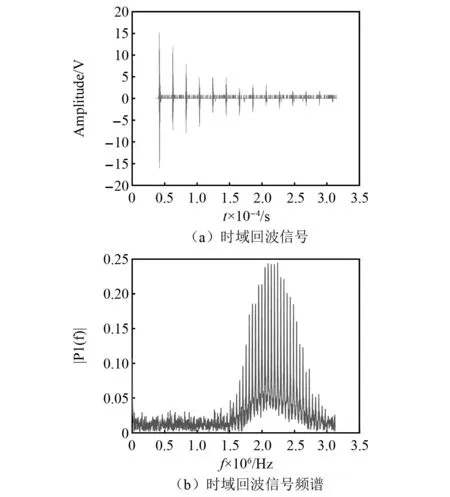
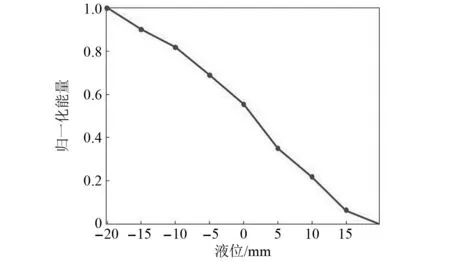
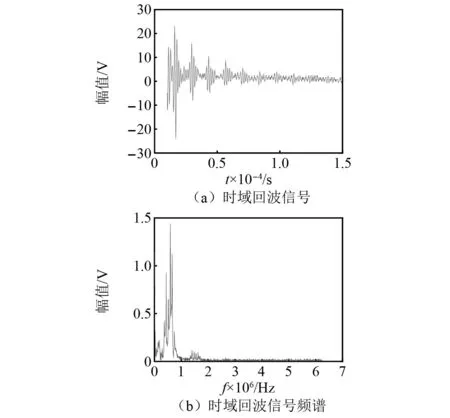
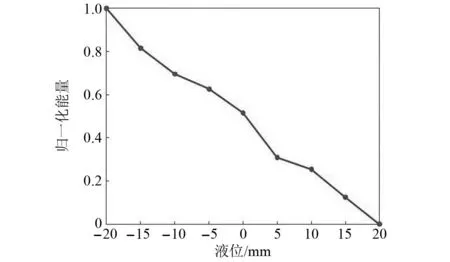
提前标定rs=1时液面完全在探头上方接收的回波信号能量Wl和rs=0时液面完全在探头下方接收的回波信号能量Wn。当0 图4 能量随液位的变化曲线Fig.4 Curve of liquid level position and energy 在COMSOL Multiphysics建立的模型如图5所示。频率为2.25 MHz、尺寸为40 mm×20 mm(长×宽) 的收发探头置于壁厚60 mm、0.6 m×0.6 m×0.8 m(长×宽×高)的长方体型Q345钢质容器的外侧壁。 图5 液罐模型Fig.5 Liquid tank mode Q345钢质容器的密度为7 850 kg/m3,弹性模量为2×1011Pa,泊松比为0.2。物理场包括弹性波和压力声学两部分。压电陶瓷所施加的激励电压如图6(a)所示。接收到的回波信号如图6(b)所示,左边方框为发射信号,右上角的波形为接收回波信号的放大图。 图6 仿真信号Fig.6 Simulated signal 以探头中心为原点建立一维y坐标。液面位置距离坐标原点分别为-20 mm、-15 mm、-10 mm、-5 mm、0、5 mm、10 mm、15 mm及20 mm等九个位置接收信号,由式(12)计算其对应能量。图7为液面位置与归一化能量之间的关系,随着液位的升高,其能量减小,与理论仿真图4趋势一致。 图7 能量随液位的变化曲线Fig.7 Curve of liquid level position and energy (12) 式中:X(k)为时域信号x(n)离散傅里叶变换;N为时域信号的点数。 频率为2.25 MHz的矩形收发的探头(长为40 mm,宽为20 mm)使用硅脂固定于如图8(a)所示的长方体型Q345钢质容器(壁厚60 mm、高0.8 m、长0.6 m、宽0.6 m)的外侧壁,容器内液体为水,图8(b)为探头、夹具及部分容器壁。探头连接到CST-8077PR脉冲发生仪的自发自收端口,脉冲信号的重复频率为100 Hz,增益为35 dB,信号端口连接到Tekronix-TBS-1102B示波器的CH1端口,使用的仪器如图8(c)所示。当超声波声束垂直入射穿过容器壁时,因容器内壁与容器内介质的特性阻抗不同,超声波在该界面将发生反射和透射,反射波沿原路径返回由探头接收显示到示波器并采集,其采样率fs=1×107Hz,采样周期为T=1×10-7s。 图8 试验装置Fig.8 Test device 利用探头频率为2.25 MHz和0.5 MHz分别对壁厚60 mm和40 mm,进行了罐内液位变化的测试试验。 探头频率为2.25 MHz,带宽为1.5 MHz,下限频率为1.28 MHz、上限频率为2.83 MHz,壁厚为60 mm,脉冲宽度为200 ns、重复频率500 Hz。采集到的时域回波信号如图9(a)所示。对采集到的时域回波信号进行快速傅里叶变换,得到其频谱如图9(b)所示。 图9 0.5 MHz探头接收的信号Fig.9 The signal received by the 0.5 MHz probe 初始液位在探头底部位置,随着液位升高,Q345钢-水界面比Q345钢-空气界面透射波的占比大,探头高度范围内空气介质占比将减小,探头接收到的回波信号能量也将减小。依据第2章的九个液位依次采集回波信号,计算其归一化能量。图10为试验的归一化能量曲线,能量随液位的上升而减小。 图10 能量随液位的变化曲线Fig.10 Curve of liquid level position and energy 计算回波信号的能量、rs及液位,如表1所示。实际液位0表示液面位于探头中心位置,液面从相对探头中心位置-20 mm(即探头底端开始)逐渐升高,间隔5 mm采集一次回波信号,探头高度范围内采集9个位置的回波信号。由式(12)计算能量,实际液位对应的能量即为该位置所测回波信号能量,随着液位的上升,固/液界面占比面积逐渐增加,固/气界面占比面积逐渐减小,透射波占比增加,能量泄漏逐渐增多,回波信号的总能量逐渐减小。实际值rs是由实际液位位置计算得到。将9个位置回波信号的能量归一化后代入占比面积表达式(11)可得到计算值rs。实际液位与占比面积计算值之差即为误差,由表1可知,实际液位为15 mm处的误差最大且最大为2.450 mm,实际液位为5 mm处的误差最小且最小为0.976 mm,其余位置的误差均小于2.450 mm。实际液位与计算所得液位基本吻合。能量随液位的上升而减小,液面位置完全位于探头下方和上方的能量与-20.000 mm和20.000 mm处的能量几乎保持一致。 表1 计算液位和实际液位Tab.1 Calculated liquid level and actual liquid level 探头频率为0.5 MHz,带宽为0.29 MHz,下限频率为0.33 MHz、上限频率为0.62 MHz,壁厚为40 mm,发射脉冲电压为100 V,发射脉冲的宽度为1 000 ns、重复频率为500 Hz。其余条件均不变的条件下,依据上述试验过程进行测试。示波器采集的时域回波信号如图11(a)所示,其频谱如图11(b)所示。 图11 2.25 MHz探头接收的信号Fig.11 The signal received by the 2.25 MHz probe 依据2.25 MHz的计算方法,得到0.5 MHz归一化能量随液位变化的关系如图12所示。随着液位的上升能量逐渐减小。 图12 能量随液位的变化曲线Fig.12 Curve of liquid level position and energy 将九个液面位置的归一化能量代入式(11)得到对应的液位在投影矩形中的占比面积rs的计算值,结果如表2所示。由表2可知,实际液位为5 mm处的误差最大且最大为2.465 mm,实际液位为15 mm处的误差最小且最小为0.023 mm,其余位置的误差均小于2.465 mm。 表2 计算液位和实际液位Tab.2 Calculated liquid level and actual liquid level 表1和表2的结果表明本文提出的声束内壁投影模型能较好地计算得到探头高度范围内能量随液位变化的关系,且误差均小于2.465 mm,不仅可以判断液位的有无,可以计算出探头高度范围内液面的位置。同时该模型对于不同壁厚不同频率均有效。 置于液罐外壁液面高度附近处的收发探头发射声束透过罐壁在其内壁产生一投影面积,建立了基于矩形活塞辐射的声束内壁投影模型,利用液体介质面积Sw与声束在容器内壁处形成的面积S的占比rs和回波信号能量之间的关系,计算出探头高度范围内接收到的回波信号能量,该能量值与液面高度近似成反比,由此定征液面位置。有限元仿真探头高度范围内接收液位上升时的回波信号,计算其能量并得到能量随液位的变化。搭建试验系统,对不同壁厚不同频率进行试验,向容器内加入液体,当液面位于探头底端时开始采集信号,采集的数据通过Matlab进行能量计算并得到能量随液位变化的关系,将能量代入理论模型中计算相对探头的液面位置。结果表明,对于不同壁厚不同频率的计算的液位位置与实际液面位置均吻合,两者的误差仅小于2.465 mm,有限元仿真计算也验证了探头接收能量与液位变化的关系。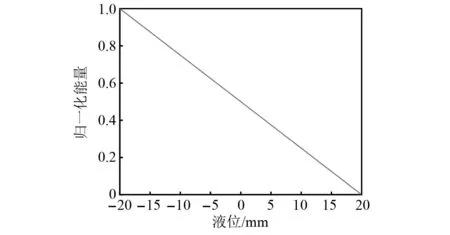
2 仿真计算
3 试验及分析



4 结 论

