精密平台磁敏智能隔振系统自适应PI控制研究

钟 灿, 黄 振, 李 旺, 浮 洁, 韩锦聿, 余 淼, 綦 松

(重庆大学 光电工程学院光电技术及系统教育部重点实验室,重庆 400044)

精密加工是一个国家机械制造的最高体现,也是一个国家科学发展水平的重要标志。复杂恶劣的微振动将会严重影响加工精度,其振动位移幅值通常在微米量级、频率在1～100 Hz。针对精密加工,采用基于磁流变弹性体(magneto rheological elastomer,MRE)的半主动隔振技术,具有参数可调[1]、响应快、功耗低的优点,尤其在微小应变下,其磁流变效应大,因此更适用于微振动隔振。它克服了被动技术中低频隔振困难与主动技术中成本高、高频易失稳的问题[2],在隔振与缓冲领域[3-5]具有广泛的应用前景。通过施加磁场,改变MRE隔振系统结构刚度和阻尼[6],进而实现振动衰减。

对于结构确定的MRE隔振系统,减振性能的优劣由控制算法决定。比例积分微分(proportional integral differential,PID)控制算法控制以其结构简单、可调参数少等优点,被广泛用于工业控制系统中,超过95%的过程控制是基于PID控制设计的[7-8]。其核心思想是通过误差的比例、积分和微分三种形式的线性组合,实现对被控对象的控制,且针对确定激励振动有好的抑制效果[9]。但对实际以精密平台为精密加工载体的对象,如滚珠丝杆进给系统中工作平台的振动频率、幅值受进给速度、位置的变化而改变[10];铣床旋转、切削等加工过程中,其旋转工作台的固有频率会随着刀具形状变化而改变[11-12]。当激励发生变化时,传统的PID控制器控制效果变差,因此需要PID控制器具有自适应性。此外,由于磁流变弹性体隔振器具有快速的响应时间(毫秒级),与微分控制相关的动态性能通常可以满足要求,因此自适应PI控制可有效解决时变振动抑制。

现有针对精密加工对象的自适应PI方法仅有主动模糊PID控制(压电、电磁等)[13-15]。该方法通过设计模糊规则调控PID参数或采用模糊控制器与PID控制器切换控制,但其仅以误差幅值作为控制器输入,并未考虑频率变化对控制性能的影响。事实上,对周期性的振动信号,其控制效果不仅与激励幅值有关,还与频率有关。因此,实时辨识振动频率并实现频率、幅值自适应是控制的难点问题。

进行自适应律设计时可以通过优化方法获得不同振动激励频率、幅值下最优控制参数。遗传算法是一种基于自然选择和演化机理的优化算法,主要特点表现为不依赖于梯度信息的群体搜索策略和群体中个体间的信息交换,适用于处理传统搜索方法难以解决的复杂非线性问题[16]。获取频率、幅值依赖的最优控制参数的前提是实时识别激励频率,采用傅里叶变换的方法识别频率会产生严重的时滞,难以保证其实时性,控制效果变差。因此本文提出了一种新的频率识别办法,通过被动模型建立激励与响应的幅值比和频率的关系,将方程中的频率“消掉”,从而获得仅依赖于激励和响应幅值的自适应律,实现无需辨识激励频率即可自适应频率的变化。

针对以上分析,本文创新性提出了一种基于遗传算法的自适应PI控制器。首先通过遗传算法寻优获得不同幅频激励下的最优PI参数值;再根据被动参考模型获得仅依赖于激励和响应幅值但隐含频率(无需直接辨识频率)的自适应律。最后通过数值仿真和试验两方面分析对比了在传统PI控制算法与自适应PI控制算法下,基于精密加工平台MRE隔振系统的振动衰减性能。

1 磁流变弹性体隔振系统动力学模型

MRE隔振系统单自由度系统如图1所示,k0和c0分别为MRE隔振系统在没有外加电流情况下的刚度与阻尼,而Δk和Δc则表示MRE隔振系统在励磁电流作用下的刚度和阻尼的变化量,m为隔振对象的质量,x1和x2分别为激励位移与被隔振对象的绝对位移,xr=x2-x1为被隔振对象的相对位移,该系统的动力学特性可由以下微分方程表达

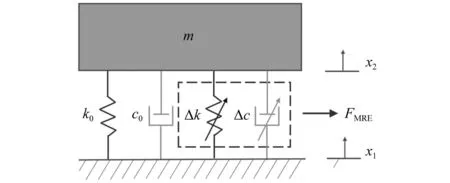
图1 MRE隔振系统单自由度动力学模型Fig.1 MRE vibration isolation system with one degree of freedom dynamics model

(1)

励磁电流作用下MRE隔振器产生的驱动力为

(2)

MRE隔振器的半主动控制条件可表示为

(3)

式中:F为MRE隔振器输出的控制力;Fc为控制器计算输出的期望力;Fmax是MRE隔振器能输出的最大控制力。

(4)

2 基于遗传算法的自适应PI控制器设计

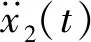
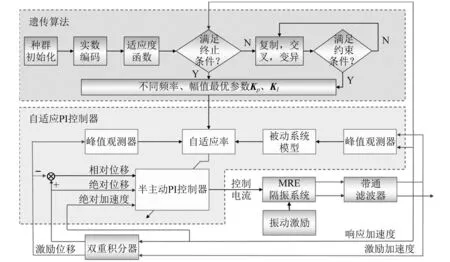
图2 基于遗传算法的自适应PI控制优化流程图Fig.2 Adaptive PI control optimization flow chart based on genetic algorithm

(5)

比例因子KP、积分因子KI可根据激励和响应位移峰值、频率进行实时调节。激励位移峰值由峰值观测器直接测得,激励位移频率则根据峰值观测器测得的被动参考模型中负载加速度峰值和激励加速度的峰值来实时获取。下面分别对峰值观测器、被动系统模型和自适应律进行介绍。

2.1 峰值观测器判断

采用峰值观测器实时获取信号x(t)的峰值Ax(t),其函数如式(4)所示,Ax(kT)为采样时间kT时的激励加速度峰值,T为控制系统的采样周期。图3为峰值观测器获取信号峰值的原理示意图,判断过程主要存在3种情况:

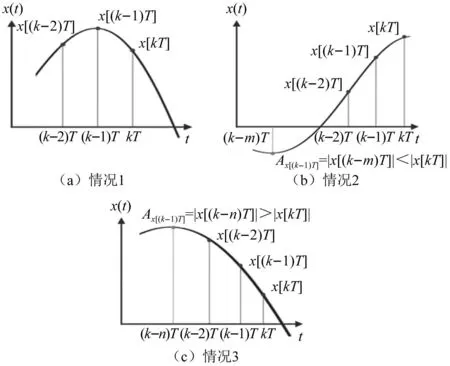
图3 峰值观测器原理Fig.3 Peak observer principle

情况1:若x[kT]-x[(k-1)T]与x[(k-1)T]-x[(k-2)T]的乘积为负且x[(k-1)T]≠0时,则判断上一时刻为峰值,取其绝对值x[(k-1)T]为峰值;

情况2:若x[kT]-x[(k-1)T]与x[(k-1)T]-x[(k-2)T]的乘积为正且x[kT]的绝对值大于上一时刻的峰值Ax[(k-1)T]时,则判断当前时刻为趋近于达到峰值,此时峰值应更新为|x[kT]|;

情况3:若存在其他情况,例如当x[kT]-x[(k-1)T]与x[(k-1)T]-x[(k-2)T]的乘积为正但x[kT]的绝对值小于上一时刻的峰值Ax[(k-1)T]时,则判断当前时刻为远离峰值或尚未趋近于达到峰值,此时峰值应保持为上一时刻峰值Ax[(k-1)T]。

2.2 被动参考模型

为对精密加工半主动隔振平台的控制条件提供依据,需要对MRE隔振系统进行参数辨识,辨识结果如表1所示。

表1 精密加工半主动隔振平台参数辨识结果

由MRE隔振系统的单自由度动力学模型可知其为二阶系统,根据表1中的参数可辨识出系统在零场下的被动模型传递函数为

(6)

图4将辨识得到的被动模型与试验结果进行对比,在20～160 Hz,其拟合优度R2约为0.96,二者吻合度较高,证实了所建被动模型的准确性。

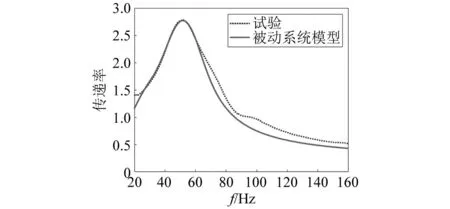
图4 MRE隔振系统被动模型辨识结果与试验结果对比Fig.4 Comparison of identification results of passive model of MRE vibration isolation system with experimental results

2.3 基于遗传算法的PI因子自适应律设计

由半主动控制条件知,MRE 隔振器的输出力与相对位移与隔振结构绝对位移的乘积相关。实际上,输出力的大小主要取决于负载的绝对位移,相对位移仅用于半主动控制条件的判定。因此,以负载的归一化绝对加速度作为反馈变量,并将其均方根值作为遗传算法中的适应度值,分别对不同激励条件下的自适应因子进行寻优,其中,遗传算法的参数设置如表2所示。

表2 针对PI因子寻优的遗传算法参数设置

基于Matlab仿真软件,通过遗传算法得到的优化结果如表3、表4所示。

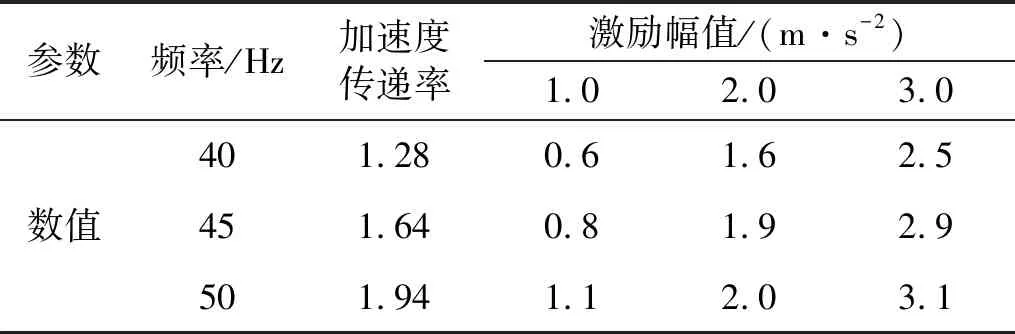
表3 基于遗传算法的KP寻优结果

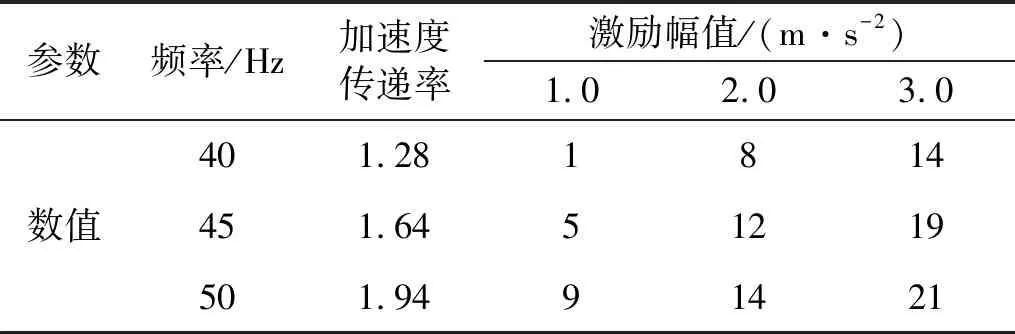
表4 基于遗传算法的KI寻优结果

由表3～4可知,在该频带的频率范围内,比例因子KP、积分因子KI的取值与激励幅值、激励频率有关,以激励幅值A1(t)、响应幅值A2(t)为自变量,自适应率如式(7)所示。将其转化为激励幅值与频率,拟合结果如图5所示。

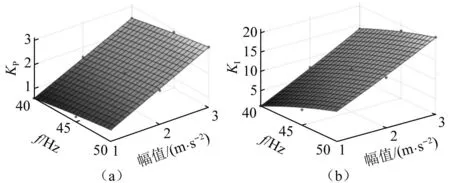
图5 自适应因子与激励峰值、频率拟合结果Fig.5 The fitting results of adaptive factor with excitation peak and frequency

(7)

式(7)为比例因子KP、积分因子KI自适应律,该自适应率根据被动参考模型建立加速度传递率和频率的关系,将方程中的频率“消掉”,并拟合获得PI参数的自适应律;再以激励与响应的幅值比替换加速度传递率,从而获得仅依赖于激励和响应幅值但隐含频率的自适应律,实现无需辨识激励变量即可自适应频率的变化。

3 仿真结果及分析

为了证明所提出的模型参考自适应PI控制器的优越性,对变频率变幅值激励下的振动衰减情况进行仿真分析。仿真采用的负载、MRE隔振器参数如表1所示。设置激励振幅在1 s内从1.0 m/s2线性增加到3.0 m/s2,同时其频率从50 Hz减小到40 Hz。其中传统PI控制器的参数是基于激励加速度幅值为1.0 m/s2,频率为50 Hz情况下设计的。PI控制器的自适应因子的调节过程如图6所示。图7比较了传统PI控制器和自适应PI控制器作用下系统的加速度响应及加速度均方根衰减率。

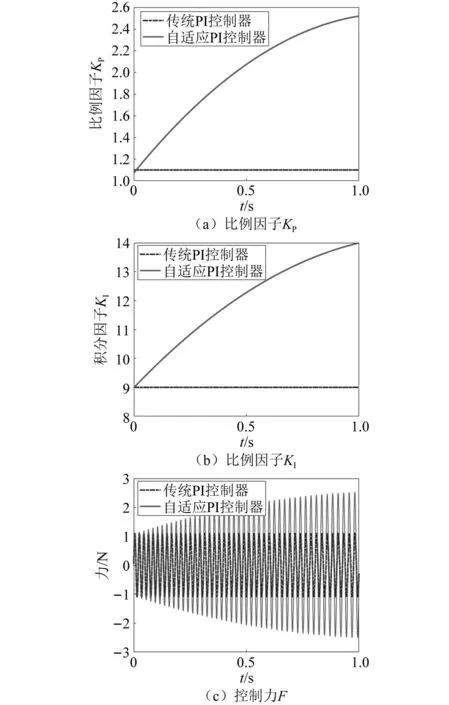
图6 变频变幅激励下控制器参数仿真调节过程Fig.6 Controller parameters simulation adjustment process under variable frequency and amplitude excitation

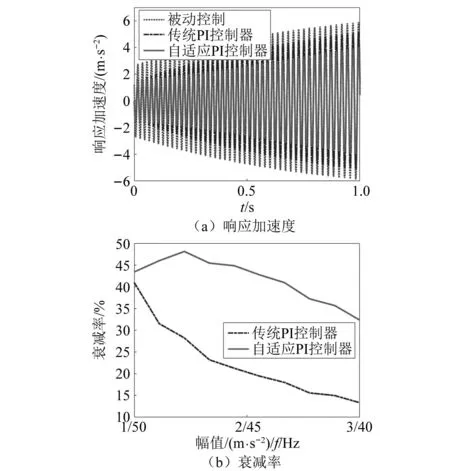
图7 变频变幅激励下自适应PI控制仿真结果Fig.7 Simulation results of adaptive PI control under variable frequency and amplitude excitation

结果表明,自适应PI控制器具有更好的控制效果。被动控制、传统的PI控制和自适应PI控制在激励幅值、频率变化的范围内的均方根分别为3.32 m/s2、2.68 m/s2和2.00 m/s2,传统PI控制和自适应PI控制分别衰减了19.3%、39.8%,其中传统PI和自适应PI控制输出力的均方根分别为0.79 N、1.46 N。随着激励幅值的增加、频率的减小,传统的PI控制效果逐渐变差,衰减率为13.3%,而自适应PI控制器的衰减率仍能达约32.4%的衰减效果。

4 试验结果及分析

4.1 试验系统

PI隔振试验系统如图8所示。试验采用的负载、MRE隔振器参数如表1所示。MRE隔振器安装在电磁振动台台面上,负载质量块与隔振器的顶部通过螺杆连接。电磁振动台为隔振器提供加速度激励信号,两个压电式加速度传感器分别测试电磁振动台给予的基础激励及负载上的响应加速度。传感器所测得的信号为电荷信号,通过信号调理器转换为电压信号,然后由dSPACE进行采集。PI控制器输出的控制电流通过电流驱动器施加给MRE隔振器,直流电源为电流驱动器供电,其中电流探头用以检测电流信号并将其转换为电压信号。

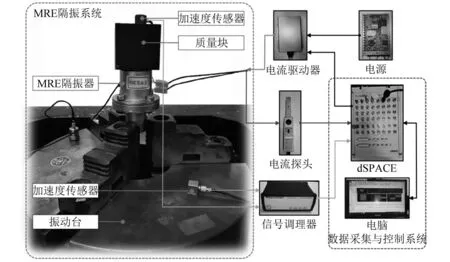
图8 PI隔振试验系统实物图Fig.8 PI vibration isolation test system physical diagram

4.2 试验结果

在该试验中,激励加速度信号幅值从1.0 m/s2线性增加到3.0 m/s2、频率从50 Hz减少到40 Hz,在不同的控制器下,加速度响应、控制电流和衰减率如图9、10所示。

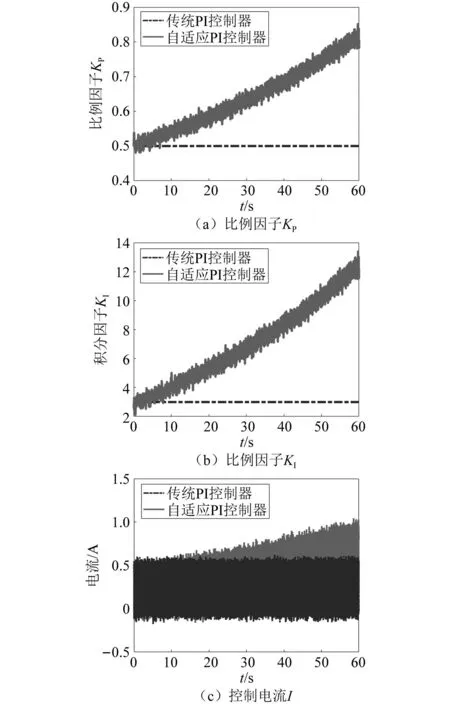
图9 变频变幅激励下控制器参数试验调节过程Fig.9 Experimental adjustment process of controller parameters under variable frequency and amplitude excitation

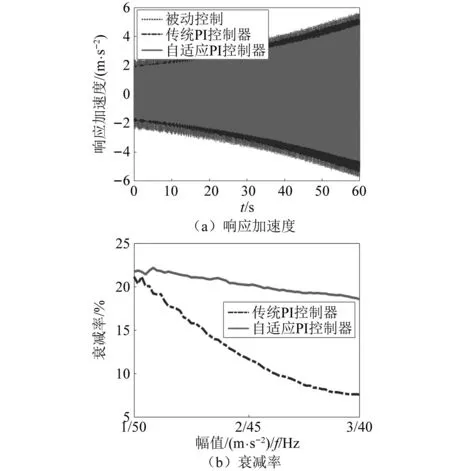
图10 变频变幅激励下自适应PI控制试验结果Fig.10 Experimental results of adaptive PI control under variable frequency and amplitude excitation

结果表明,自适应PI控制器具有更好的控制效果,被动控制、传统的PI控制和自适应PI控制在激励幅值、频率变化范围内的均方根分别为2.69 m/s2、2.40 m/s2和2.15 m/s2,传统PI控制和自适应PI控制分别衰减了10.8%、20.1%,其中传统PI和自适应PI控制输出电流的均方根分别为0.30 A、0.41 A。随着激励幅值的增加、频率的减小,传统的PI控制效果逐渐变差,衰减率为7.6%,而自适应PI控制器仍能达约18.6%的衰减效果。

将试验结果与仿真结果进行对比,如图11所示。可以发现PI控制器的试验结果较仿真结果不理想,这是因为试验中控制系统各部分存在延时,系统的延时会导致控制的滞后且严重地影响控制器的性能,减弱控制器的控制效果;同时,在实际试验中未考虑隔振系统的逆模型,实际输出的控制电流与计算的控制力具有偏差,因此降低了试验的控制性能。

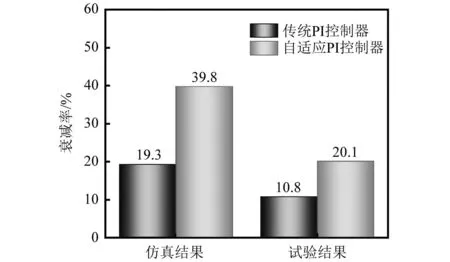
图11 试验结果和仿真结果衰减率对比图Fig.11 Comparison of attenuation rates between experimental results and simulation results

5 结 论

针对精密加工平台振动频率、幅值的时变特性,本文提出自适应PI控制方法。通过遗传算法对不同频率、幅值下的PI控制器参数进行寻优,得到优化后控制器的自适应律,从而设计自适应PI控制器。试验表明所设计的自适应PI控制器对时变激励(40-50 Hz、1-3 m/s2)振动抑制优于传统PI控制器和被动控制,其中传统PI控制器衰减率仅为10.8%,而自适应PI控制器衰减率可达20.1%。