多层交通荷载下非对称一体化地下结构的动力响应

钱劲松, 陈 正, 欧阳韦,2, 刘海洋, 周毅恒

(1. 同济大学 道路与交通工程教育部重点实验室,上海 201804;2. 中电建路桥集团有限公司,北京 100160)

城市地下交通设施是城市道路系统的地下延伸,其多以隧道的形式通行车辆或列车,不仅节约地面空间,且对周围环境和既有城市道路影响小,是解决城市交通饱和问题的关键。现有将地铁隧道、城市快速路、管廊合建的结构,具有断面非对称、异形和结构复杂等特点,此类结构力学状态受基础条件、施工工艺、断面形式、荷载组合等因素影响,存在结构受力不均和应力集中等现象。另一方面,受道路平整度、轨道不平顺等因素的影响,车辆与列车通过隧道时会产生振动荷载,进而引起地下结构的动力响应,特别是多类交通动荷载综合作用时,引起的地下结构动力响应更加明显,对结构安全性能和服役寿命产生显著影响。

针对交通荷载对地下结构的影响,学者们已展开了大量研究。然而,大部分研究往往关注于地铁列车高频振动产生的激振力对结构的影响。例如,在20世纪列车发展迅速的时期,部分学者基于解析或半解析的方法预测了列车荷载引起的振动效应,结果表明列车荷载对地铁结构的影响较大[1]。为了进一步探究地铁列车荷载的影响,Zhu等[2-4]将地铁列车荷载定义为一种长期地循环荷载,分别研究了其对周围土体与路面结构沉降的影响。白建方等[5-6]分析了列车荷载引起的基坑支护围护结构以及隧道结构本身的动力响应特征。

此外,随着数值模拟系统软件的开发与应用,基于数值方法模拟分析地下隧道结构响应的效率显著提高,也为地下结构受到复杂交通荷载的响应计算提供了可能。大量学者采用数值仿真技术对高速列车荷载引起的隧道动力响应和对周围环境影响的问题展开了仿真分析。黄光强等[7-9]采用数值仿真的方法,对高速列车振动荷载作用下不同形式断面的动力响应特性进行分析,证明隧道的断面形状对其结构的动力响应影响较大,在研究列车振动荷载诱发的结构动力响应时应考虑列车移动效应。王建炜等[10-11]建立了隧道-土体系统的三维动力有限元模型,对公路和轨道交通荷载各组合模式的动力响应规律进行分析,明晰两种荷载共同作用时的线性叠加作用。杨宗桦等[12-13]分析了地面交通车速和隧道埋深等因素的多种工况,探究了交通动载对浅埋隧道动力响应的影响。严武建等[14-16]不仅分析了浅埋隧道的动力响应,还针对地表沉降和场地振动等进行分析,提出相关控制基准值。加武荣等[17-19]针对交叉隧道结构,研究了围岩结构、行车速度、隧道交叉角度等对结构动力响应的影响。上述研究表明,数值仿真技术已广泛应用于地下结构受到交通荷载的响应计算分析中,并且交通荷载和隧道断面形式对隧道结构的动力响应不可忽视,然而现有研究多集中于单一交通荷载模式作用在对称的隧道结构的情况,对于多层交通荷载作用于非对称地下结构的动力响应有待于进一步研究。

因此,本文依托义乌某在建地下立体交通工程,聚焦长距离并线的市政交通隧道与地铁隧道一体化结构,建立精细化有限元模型,考虑多层交通荷载的直接作用,仿真计算偏压作用下非对称结构在长期运营过程中的结构动力响应特征,明确动力响应显著部位和隐患部位。为评价复杂地下立体设施结构动力响应安全性提供参考,并为地下非对称一体化结构的优化设计、运营期监控与维护提供理论依据。

1 工程概况

义乌某在建地下立体交通工程结构典型断面布置如图1所示。工程施工采用明挖顺作法,典型断面实际尺寸宽40 m,深16 m,地下一层位置为市政交通层,层顶标高约为-3 m,地下二层位置为轨道交通层,层顶标高约为-9 m,均采用单箱双室矩形结构。该一体化结构在运营期受到多层交通荷载的作用,主要包含地面层双向四车道的车辆荷载、市政交通层双向四车道的车辆荷载以及轨道交通层的地铁列车荷载。多层交通荷载共同作用于一体化主体结构时,主体结构会产生复杂的动力响应,在长期的循环荷载作用下,安全性受到极大影响。

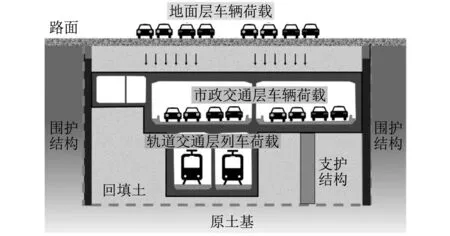
图1 主体结构交通荷载示意图Fig.1 Schematic diagram of traffic load on the main structure

基坑围护采用钻孔灌注桩,利用预应力锚索加固,宽度较大部分采用多道钢管内支撑;轨道交通工程区间位于主线隧道下方,基坑为坑中坑形式,坑中坑采用放坡形式,采用土钉墙围护,如图2所示。

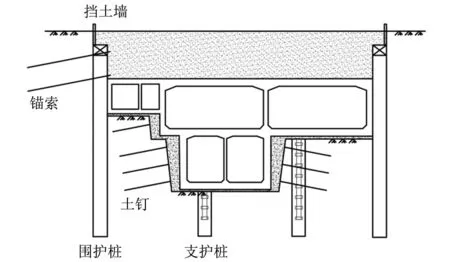
图2 施工支护结构形式Fig.2 The form of construction support structure

场地主要由填土、淤泥质粉质黏土、粉质黏土、泥质粉砂岩等组成。结构深度相关各岩土层参数如表1所示。

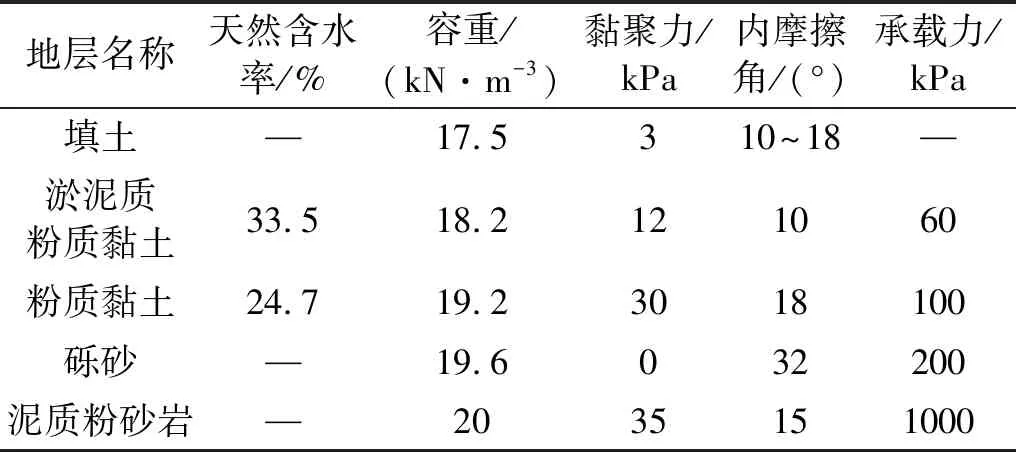
表1 地层参数

2 数值仿真

2.1 模型建立

根据实际断面几何尺寸,建立一体化主体结构几何模型,包括侧墙、中墙、顶板、底板等。为减小边界条件的设置对分析计算的影响,横向增加左右10 m土体结构,底部向下取30 m基岩结构,最终模型截面尺寸确定为60 m(宽)×46 m(深)×40 m(轴)。为合理施加列车集中力荷载,参照CRTSⅡ型板式轨道,按照实际尺寸,建立地铁列车钢轨、扣件等轨道结构,如图3所示。主体模型采用C3D8R实体单元,主体结构附近网格加密,为消除应力波的反射,在土体模型的侧面和底面划分区域,采用CIN3D8无限单元,如图4所示。将一体化结构重力和荷载作用下的静应力场作为初始应力,在隧道与轴向垂直的截面用ABAQUS软件的load模块施加所有方向的固定约束。为考虑施工期影响,整体模型除了包括混凝土主体结构外,还包括土体结构、围护结构和支护结构。其中,土钉结构采用T3D2单元进行模拟,围护结构和支护结构采用C3D8R实体单元,如图5所示。

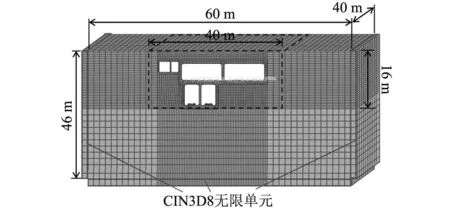
图4 主体结构模型图Fig.4 Model diagram of the main structure

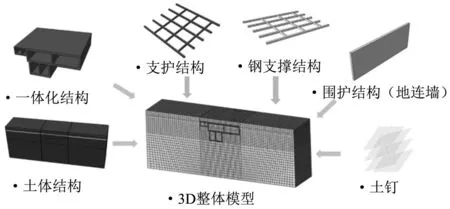
图5 3D整体模型组成Fig.5 Composition of the 3D overall model

2.2 模型参数与接触设置

在仿真分析中,合理的本构模型选择和正确的参数设置是确保模型分析正确的前提。本文重点关注的是岩土体和地下一体化结构在交通荷载作用下的力学响应特征,且考虑到原土基的开挖和卸荷过程,开挖土体采用修正剑桥本构模型,模型参数如表2所示。一体化结构采用C35混凝土材料,选择损伤塑性模型作为主体结构的材料本构模型。地铁轨道结构采用弹性本构模型,仅在弹性范围内变化的岩石土层与围护结构则直接采用弹性本构,其他各材料参数设置如表3所示,其中回填土体的内摩擦角为24.2°,黏聚力为 36.6 kPa。

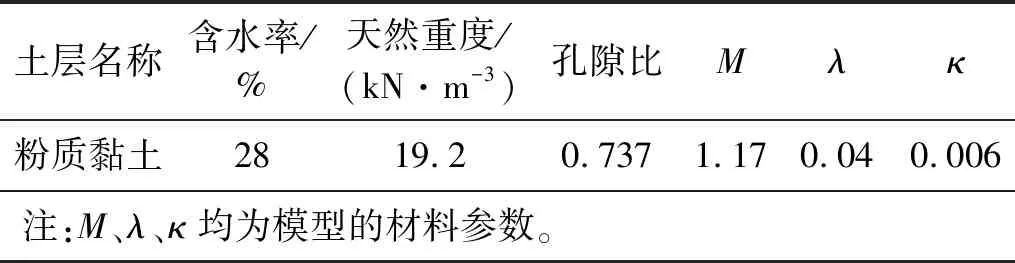
表2 岩土体本构参数

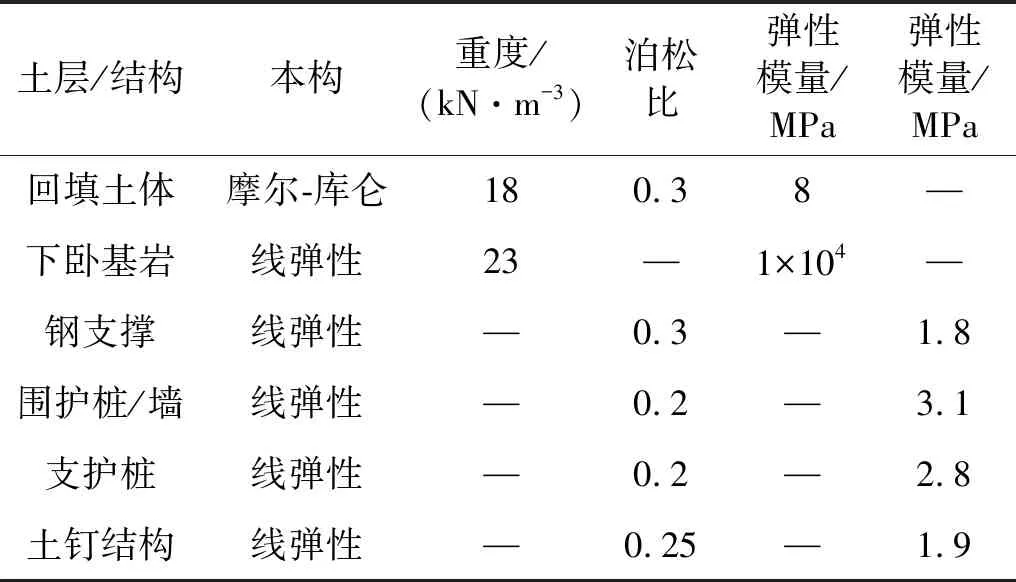
表3 其他土层与结构参数

土体阻尼采用最常用的瑞利阻尼,在ABAQUS软件中用质量阻尼系数α和刚度阻尼系数β来设置材料的阻尼大小,由模型的两个固有频率和阻尼比计算得到,本文中取土体的阻尼比ξ=0.03,一阶自振频率ω1=4.27 rad,二阶自振频率ω2=5.43 rad,计算得到阻尼系数α=0.143,β=0.006。

此外,地下一体化结构中主体结构、轨道结构和岩土体结构之间复杂的接触与约束设置显著影响动力响应分析结果。本文采用添加土弹簧的方式实现土体和结构物间接触的模拟,参照GB 50909—2014《城市轨道交通结构抗震设计规范》[20]中的经验公式,各结构层位置弹簧刚度取值如表4所示。钢轨和轨道板之间也采用弹簧单元模拟,垂向刚度和阻尼分别为5×107N/m和7.5×104N·s/m。

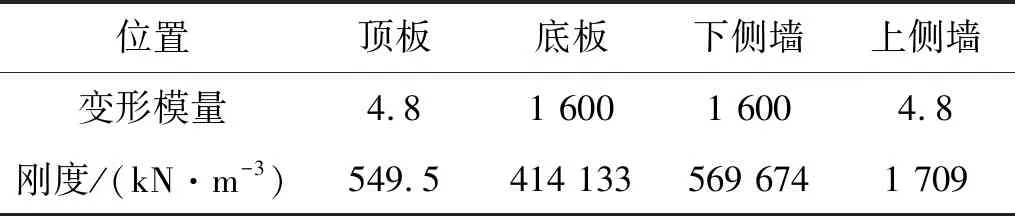
表4 典型断面土弹簧刚度

2.3 交通荷载模拟

2.3.1 车辆荷载

对地下一体化结构瞬时动力响应进行分析时,考虑车辆和结构之间的相互作用关系,不考虑车辆自身引起的振动响应。使用JTG D60—2015《公路桥涵设计通用规范》[21]规定的车辆荷载标准值模拟车辆荷载在明挖隧道中的作用[22-24],采用半波正弦荷载来模拟随时间变化的车辆荷载。车辆的车轮简化为长0.6 m、宽0.2 m的长方体薄块,车轮轴间距取值为1.4 m,前后车轮间距1.8 m,对典型断面中市政交通层部分主道取双向4车道布置车轮数,在长方体薄块的边界条件中设置80 km/h的车速来模拟车辆实际中相向的空间位置移动,如图6所示,车辆荷载时程曲线如图7所示。

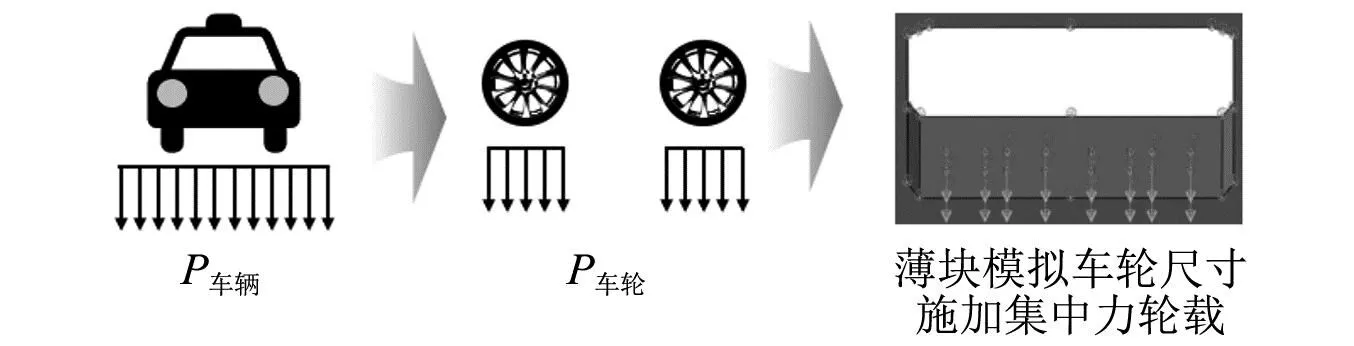
图6 车辆荷载有限元模拟Fig.6 Finite element simulation of vehicle load

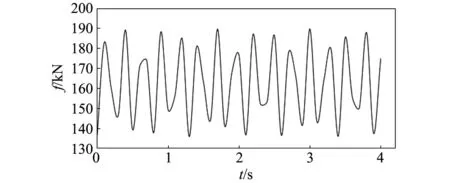
图7 车辆荷载时程曲线模拟Fig.7 Simulated time history curve of vehicle load

2.3.2 列车荷载

基于Metrikine等[25]建立的平面动力相互作用模型与列车振动,计算高速地铁列车的理论振动荷载,模拟地铁列车的激励。考虑列车轴重、悬挂质量、轨道组成以及行车速度等方面的影响,用一个类似激励力的函数来模拟列车动荷载,以B型地铁为例,取车轮静载设为80 kN,列车时速设为120 km/h,考虑3个典型的不平顺波长。在ABAQUS软件中采用集中力的方式施加于钢轨,如图8所示,地铁列车的荷载时程曲线如图9所示。

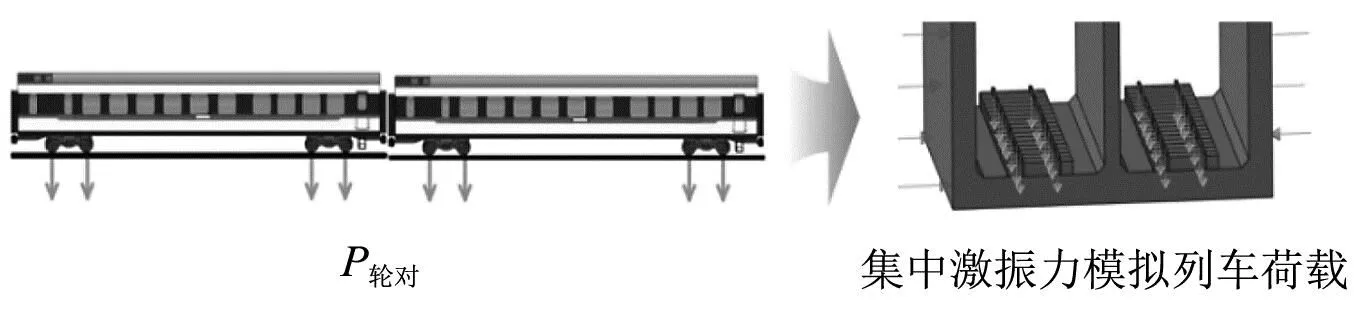
图8 列车荷载有限元模拟Fig.8 Finite element simulation of train load

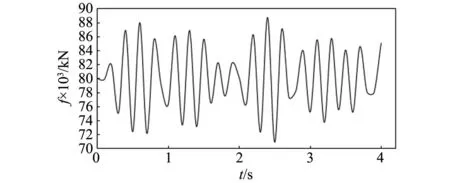
图9 地铁荷载时程曲线模拟Fig.9 Simulation time history curve of subway load

2.4 分析点位

由于一体化结构的非对称性,选取市政交通层和轨道层左右顶板、底板、侧墙、中墙的中部、左右顶角与底角为控制点,如图10所示。在后续分析中,结构左右两侧隧道将以左幅和右幅作区分。

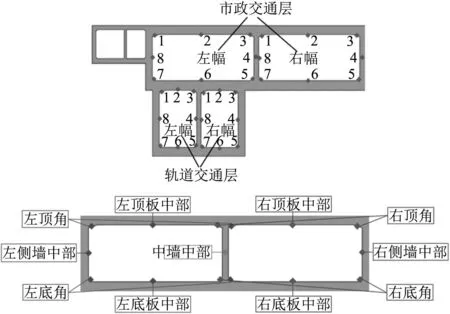
图10 断面特征控制点Fig.10 Control points for cross-sectional features

3 模型验证

为验证仿真模型的可信度,本研究对比分析了车辆65 km/h、列车120 km/h同时经过断面时一体化结构的加速度和动应力实测值与模拟值,结果如图11所示。基于数值模拟分析的加速度与动应力随时间变化规律与实测曲线基本吻合,所建立的模型合理可靠。

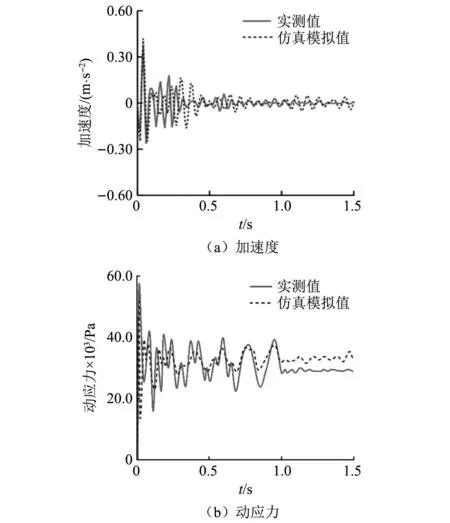
图11 结构动力响应实测值与模拟值对比Fig.11 Comparison of measured and simulated values of structural dynamic response

4 动力响应分析

4.1 非对称结构动力响应分布

为了分析多层交通荷载组合作用下一体化结构的振动响应规律和应力作用分布,揭示振动以及动应力集中的关键部位,以地面车辆和市政交通层车辆车速80 km/h,轨道交通层地铁列车车速120 km/h共同经过断面为例进行仿真分析。

4.1.1 振动响应分布

结构振动竖向加速度响应结果如图12所示,多层交通荷载同时作用于断面时,由于结构和荷载的非对称性,一体化结构市政交通层和轨道交通层左右幅的振动响应分布均呈现明显的非对称关系。对于市政交通层而言,振动响应显著位置均位于顶板或底板的中部。这是因为顶板和底板中部受其它部件约束较少,荷载作用下更容易产生振动。此外,相比而言,左幅顶板中部和底板中部竖向振动均较大,加速度最大处可达0.7 m/s2;而右幅仅在顶板中部位置振动响应相对较大,加速度达到0.5 m/s2。一方面,因为轨道层位于交通层左幅下方,导致轨道交通振动效应对左幅的影响更大;另一方面,交通层右幅下方和右侧受土体和支护围护结构约束较大,进一步减小了右幅的振动响应。

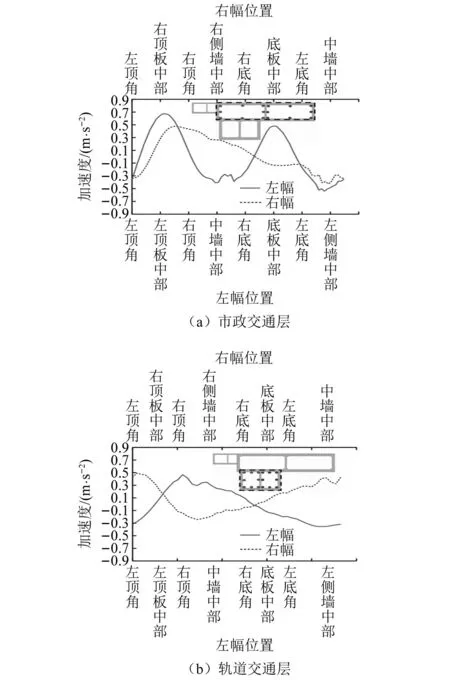
图12 结构竖向加速度分布Fig.12 Distribution of vertical acceleration in structures

对于一体化结构轨道交通层而言,其振动响应略小于市政交通层,其原因可能是轨道交通层的深度更深,地面车辆和市政交通层车辆振动效应向下传导时被不断削弱。另一方面,由于轨道交通层受到土钉支护与桩基支撑,即使承担了额外的轨道交通荷载,加速度幅值依然较市政交通层更小。此外,轨道交通层振动响应较大位置位于左右顶角和中墙中部,加速度最大处达0.4～0.5 m/s2。这是因为中墙处受市政交通荷载振动效应影响明显。因此,区别于常规的拱式或矩形对称式的断面结构,非对称一体化结构动力响应十分复杂,分析中应重点关注市政交通层左右幅顶板中部以及轨道层顶角、中墙中部的振动响应。

4.1.2 应力分布

某一时刻结构各部分的主应力分布云图如图13所示,对于混凝土结构而言,最容易产生拉应力损伤,因此在研究中最为关心的是拉应力集中的部位。市政交通层拉应力主要于左右顶板中部位置较大,轨道交通层拉应力主要于侧墙中部、底角等位置较大。

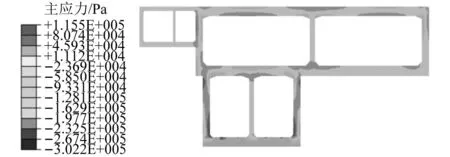
图13 结构主应力云图Fig.13 Cloud diagram of structural principal stress

进一步提取分析上述点位的应力随时间变化规律,如图14所示。当车辆荷载与地铁荷载通过断面时,市政交通层左顶板中部、底角处和轨道交通层底角拉应力出现明显突变,并在0.3 s内快速衰减,变化幅度可达0.05～0.10 MPa,而右顶板中部的应力变化则相对较小,达到0.03 MPa。其中,轨道交通层由于受到额外的地铁荷载作用,底角动应力的峰值最高,达到0.10 MPa,应力衰减幅度也更小,这是由于地铁车辆荷载的连续作用,使得动应力始终维持较高的水平。

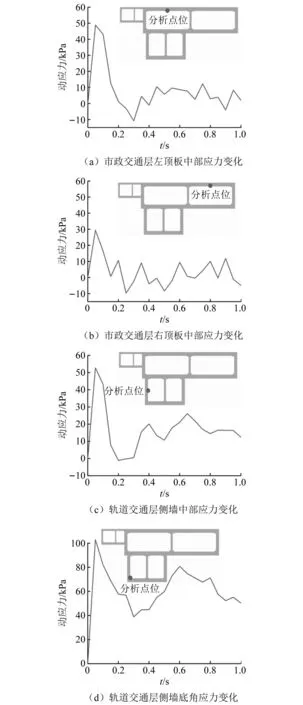
图14 动应力显著点位的应力变化Fig.14 Stress changes at significant points of dynamic stress

考虑到混凝土结构长期循环作用下的水平拉压和剪切疲劳损伤,市政交通层左顶板中部和轨道交通层侧墙中部、底角处易产生结构裂缝,影响地下结构运营安全性能和服役寿命。

4.2 多层交通荷载叠加作用

4.2.1 振动响应叠加作用

明确地下一体化设施结构动力响应整体分布情况后,针对受力集中或振动强烈的点位,进一步分析地面层双向四车道的车辆荷载、市政交通层双向四车道的车辆荷载以及轨道交通层的地铁列车荷载三层交通荷载逐级叠加作用时结构的动力特征。由于地下一体化设施全线受到车辆荷载情况较复杂,但实际运营过程中长期受到列车荷载作用,考虑以下三种工况进行对比分析。

工况一:仅承受轨道交通层地铁列车荷载;

工况二:承受市政交通层车辆荷载和轨道交通层地铁列车荷载两层交通荷载;

工况三:承受地面、市政交通层车辆荷载和轨道交通层地铁列车荷载三层交通荷载。

由前文分析可知,市政交通层加速度响应在顶板中部位置较大,轨道交通层加速度响应在左右顶角较大,分别选取对应的分析点位,进一步分析多层交通荷载叠加作用的影响,如图15所示。针对市政交通层顶板中部位置,工况一最大振动响应达到0.3 m/s2,后逐渐衰减;工况二相比于工况一振动响应幅值几乎不变,但衰减较慢;工况三相比于前两种工况,竖向加速度产生明显的叠加增幅作用,最大振动响应增幅为0.4 m/s2,可以认为,除地铁列车荷载外,地面交通荷载是地下一体化结构振动响应的主要影响源,且存在非线性叠加作用。

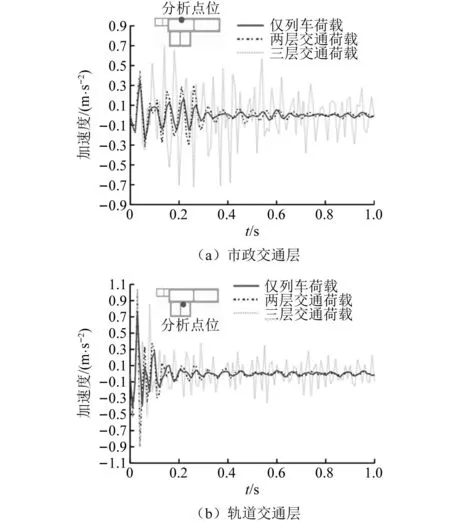
图15 三种工况振动响应变化曲线Fig.15 Vibration response curves under three working conditions

对轨道交通层右顶角而言,各工况之间同样呈现非线性叠加规律,地面交通荷载的作用使竖向加速度产生明显增幅,但列车荷载对振动响应的影响增大,这是因为轨道交通层距离列车荷载作用的位置更近。因此,可以认为在实际长期的运营过程中,尤其是地面车辆行驶密集的路段,地下一体化结构会产生更明显的竖向振动,其长期运营安全性和服役寿命易受到疲劳损伤影响,而市政交通层车辆行驶密集程度带来的影响相对较小。

4.2.2 动应力叠加作用

同样计算三种工况下,应力集中点位受振动荷载的动应力变化,分别选取市政交通顶板中部与轨道交通层左底角,如图16所示。针对市政交通层顶板中部位置,工况一最大动应力达到0.03 MPa,约为其他两个工况最大动应力值的一半,且工况三相比于前两种工况,整体动应力水平出现上升。可以认为,三层荷载的作用均会对市政交通层的动应力产生较大影响。

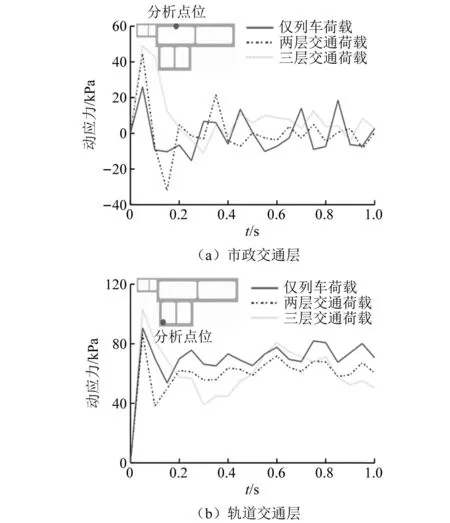
图16 三种工况动应力变化曲线Fig.16 Dynamic stress variation curves under three working conditions

对轨道交通层左底角而言,工况一最大动应力达到0.09 MPa,工况二相比于工况一动应力整体出现小幅下降,这说明复杂的支承条件与超静定结构使得市政交通层车辆荷载对轨道交通层左底角的作用力与轨道交通层列车荷载的作用力方向相反,工况三相比于前两种工况,最大动应力增大约0.02 MPa,达到0.11 MPa。

可见市政交通层与地面车辆荷载的叠加作用会使市政交通层和轨道交通层的最大动应力均增大约0.02 MPa,且地面车辆荷载的影响更显著。地铁列车荷载为一体化结构受到动应力的主要影响因素,且对轨道交通层影响显著大于对市政交通层的影响,这是因为轨道交通层距离列车荷载的距离更近。

5 结 论

本文以义乌某在建地下立体交通工程为依托,建立地下非对称一体化结构模型,模拟施加地表、市政和轨道交通荷载,分析了结构的振动响应和应力分布特征,探究了多层交通荷载共同作用产生的结构动力响应叠加规律,并与结构安全性建立联系,得到以下结论:

(1)大断面非对称一体化结构复杂且独特,荷载与支护的分布差异导致结构动力响应呈现明显的非对称性。由于轨道交通层位于市政交通层左幅的正下方,市政交通层左幅多处比右幅的振动响应高约20%,且受其它部件约束较少的顶板中部振动响应最大,达0.5～0.7 m/s2,因此在工程中应重点关注约束较少且受荷较复杂的部位。

(2)地铁列车荷载是一体化结构动应力的主要影响源,这导致距离地铁列车荷载较近的一体化结构轨道交通层最大拉应力约为市政交通层的2倍,达0.08～0.11 MPa。而在锚索、支护等因素的作用下,轨道交通层的结构竖向加速度总体上小于市政交通层,因此在轨道交通层设置更多的支护是必要的。

(3)地面车辆荷载会对一体化结构的振动响应产生较显著影响,与地铁列车荷载发生非线性叠加,使得最大振动响应增幅约0.4 m/s2,在市政交通层的振动响应中占比超50%,因此在长期运营过程中,应当更加关注地面车辆行驶密集路段的地下一体化结构。

探究了多层交通荷载对地下结构动力响应的叠加作用规律,但未分析交通荷载横向分布差异的影响。后续建议考虑运营期各交通层实际轮迹横向分布系数与最不利分布情况,针对地下结构的动力响应展开进一步研究,以指导该类工程的实施与长期运营。