考虑环境改变的部件核密度剩余寿命预测
赵 彬, 李佳娟, 石 慧, 任谦力, 康 辉
(太原科技大学 电子信息工程学院,太原 030024)
风电机组在运行过程中受风速风向等环境因素影响载荷周期波动,叶片、主轴和齿轮箱等关键部件易发生故障。其关键部件的损坏会产生经济损失并引发一系列安全隐患,因此对风电机组的关键部件进行实时监测并预测其剩余寿命,可以为更合理地制定维修策略提供依据[1-2],并且提高系统的可用性和可靠性。
现有的一些数据驱动的剩余寿命预测方法需对模型假设和参数估计,但是风电机组等大型复杂装备运行周期长且破坏性试验造价昂贵,难以获得足够的失效数据,假设的模型往往与真实的物理模型有一定差距,且参数估计的最优解不能保证全局最优。因此不适用通过统计方法[3-4]进行剩余寿命预测,而深度学习剩余寿命预测方法能够描述特征数据和剩余寿命的非线性关系,但无法得出模型剩余寿命的概率分布[5-6]。
核密度估计是一种非参数估计的方法,它从数据本身出发,无需假设数据分布[7-8]。Lang等[9]使用核密度估计对半导体制造工艺中的异常点进行监测。Hu等[10]采用核函数估计样本的局部密度,在此基础上提出了局部核回归密度估计器和分层策略结合多尺度邻域的信息细化样本的异常因子进行数据聚类及异常检测。宋仁旺等[11]考虑多退化量影响建立核密度估计和随机滤波结合的模型的系统进行剩余寿命预测,仅根据故障数据采用核密度方法估计部件初始寿命分布。
风电机组在运行中可能遭遇雷电、雨雪、侧风等恶劣天气,这些环境变化对系统运行会产生强干扰,对风机叶片、齿轮等部件造成冲击,影响系统的退化以及剩余寿命,故在建立环境变化的剩余寿命预测的模型中,环境的改变被建模为部件受到的冲击。Sidibé等[12]考虑运行环境变化导致部件可靠度改变,采用核密度的方法估计系统可靠度函数并建立基于时间的维修决策模型。Wang等[13]以液压滑阀和微机电系统为研究对象,建立了考虑冲击影响的系统可靠度模型。
受到环境影响部件的随机冲击过程与自然退化过程之间具有相关性,这种相关性不可忽视,现有很多文献都从失效的角度考虑相关性,如Wang等[14]认为累积冲击会影响系统的退化率,并且在不同退化阶段影响不同;而Gao等[15]则研究了不同种类的冲击对系统退化量和退化率影响,并推导可靠度模型;Dong等[16]认为冲击会影响系统发生的故障率,并对系统其进行维修决策;以上文献仅描述了冲击对退化单方面的影响,然而当退化到一定程度时,系统抵抗冲击的能力变弱,会使得冲击导致的失效更容易发生,由此可见,退化和冲击之间并不是毫无关联,而是相互依赖的。如Fan等[17]重点研究了退化对冲击的影响,认为自然退化影响冲击的到达率;Sun等[18]将冲击分为非致命冲击和致命冲击,认为致命冲击发生概率会随着时间的变化而增加,从冲击的角度解释了系统抵抗冲击的能力随时间变化而减弱的情况。以上的文献均是从失效的角度考虑退化和冲击的相关性,并将此过程建模为竞争性失效[19],这种失效过程缺乏考虑由环境变化而导致的阈值变化。常春波等[20]考虑系统退化后突发失效阈值会降低,建立了基于变失效阈值的竞争失效模型。Hao等[21]研究了冲击导致的硬失效与软失效之间的相关性,且认为硬失效阈值受退化状态的影响且是正比关系。Feng等[22]考虑了随机冲击的阈值和自然退化且是一种线性关系。
然而在可实时监测的系统运行过程中,用线性关系描述冲击阈值和自然退化之间的关系并不准确,剩余寿命预测建模更需要关注失效前的随机冲击过程与连续退化过程之间的随机相关性,系统受到冲击影响后可能同时改变当前退化量以及之后的退化速率,进而影响其剩余寿命分布。
本文假设恶劣环境对部件的影响为部件受到的随机冲击,在对状态监测数据随机统计分析基础上,将自适应核密度估计引入实时状态及剩余寿命预测中,提出了一种考虑环境冲击影响的核估计剩余寿命预测模型。首先,当部件运行环境改变后,其受外界环境的随机冲击影响,分析了冲击与自然退化的随机相关性;其次,利用自适应核密度估计对部件的连续自然退化过程建模,并引入可变突发失效阈值,推导出环境改变后部件核密度估计的剩余寿命,最后采用风电机组退化数据和齿轮箱磨损实测数据进行分析验证其有效性。
1 部件所受冲击与自然退化过程随机相关性分析
将部件运行的不同环境记为OEm(m=1,2,3,…),部件运行环境恶劣可能导致退化加速,其剩余寿命减少,可靠性降低,对剩余寿命预测影响较大,因此本文考虑部件环境OE1改变为环境OE2,即环境更加恶劣的情况。假设T1时刻部件运行环境改变,部件受到冲击影响,部件所受冲击与连续退化过程之间存在随机相关性,随机相关性影响可分为以下三种情形(如图1所示):
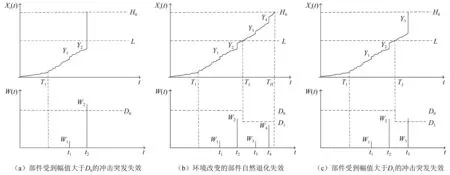
图1 环境改变的部件退化过程示意图Fig.1 Schematic diagram of the process of component degradation as the environment changes
(1) 当t
(2) 部件在环境改变受到冲击后,部件的退化状态发生改变,其中冲击的幅值为Wn,n=0,1,2,…,∞,冲击造成的退化增量为Yn,n=0,1,2,…,∞,经过t时间后退化量大于失效阈值H0,部件也会发生失效,定义为自然退化失效,TH为部件自然退化失效阈值的时刻,如图1(b)所示。
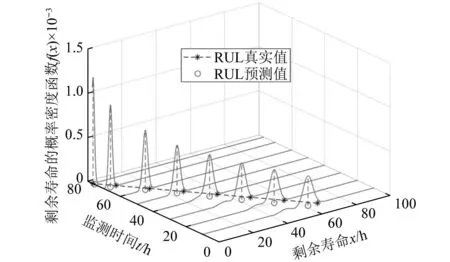
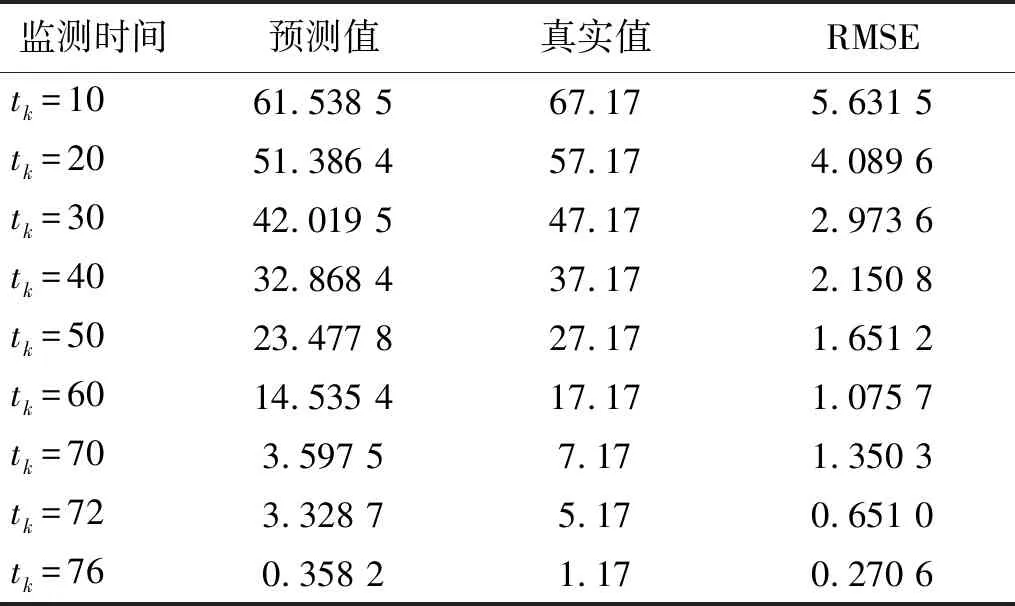
(3) 设L是使部件突发失效阈值改变的退化量阈值,环境改变后,部件运行在退化量小于L时,表明部件性能较好,受到幅值大于D0的冲击才会突发失效,当部件运行在退化量大于L小于H0阶段,表明部件性能变差,抵御外界环境变化能力降低,受到幅值较小的冲击即会发生突发失效。改变后的突发失效阈值为D1(D1 设tk为当前监测时间,假设在时间[0,tk]部件的退化增量ΔX1,ΔX2,…,ΔXk是独立同分布随机变量,f(Δx)为退化增量的概率密度函数,f(Δx)的核密度估计为 (1) 式中:k为时间[0,tk]的退化增量Xi样本个数;h为窗宽;K为核函数。 核函数的种类很多,但是不同核函数对积分均方误差的影响非常小,选择常用的高斯核函数作为核密度估计的模型 (2) 采用积分均方误差(mean integrated squared error,MISE)对核密度估计与退化增量的概率密度函数之间的误差进行测量 (3) (4) 代入高斯核函数K(Δxk)得到最优窗宽hk (5) 式中,σk为k个初始样本特征退化增量ΔX1,ΔX2,…,ΔXk的方差,则自然退化过程X(t)在不同时刻的概率密度函数g(x)可通过退化增量的概率密度函数卷积求得 (6) 部件在t时刻累积分布函数记为G(x,t),当处于环境OE1中,此时不考虑冲击影响,只考虑自然退化,可求得部件的可靠度函数为 (7) 假设部件在环境OE2受到的冲击遵循速率为λ的泊松过程{N(t),t>0},到t时刻时冲击发生次数的概率为 (8) 则环境改变后t时刻由冲击造成的退化量的总量为 (9) 若冲击幅值都小于突发失效阈值,部件不会突发失效,第n次冲击后部件不会突发失效的概率是 (10) 式中:n=1,2,…,∞,d=0,1;FW(w,Dd)为Wn的累积分布函数;Φ(·)为标准正态分布函数。 部件在时间T1从OE1进入OE2后,可能会受到多次冲击,设RS(t)为部件在时间T1环境改变后的可靠度函数;环境OE2中部件的退化不仅包含自然退化,也包括冲击引起的退化,因此其退化过程建模为 XS(t)=X(t)+S(t) (11) (1) 部件运行环境刚刚改变还没有受到冲击,此时,考虑部件不发生自然退化失效的概率 RS1[t|N(t)=0]=P[X(t) (12) (2) 改变环境后到t时刻时冲击次数不为0,若部件的退化量XS(t) (13) (3) 改变环境后时刻受到多次冲击,部件退化量H0>XS(t)>L,突发失效阈值发生改变,将冲击分为两个阶段,假设第j-1个冲击时,部件的退化量XS(tj-1) (14) 综上所述,部件在t时刻的可靠度为 (15) 将式(12)、式(13)和式(14)代入式(15)可得系统可靠度函数表达式为 (16) 式中,tj-1与tj分别为第j-1次冲击到达的时刻和第j次冲击到达的时刻,均为随机变量,计算过程中可用其均值替代。其推导过程为: 设{N(t),t≥0}是到达率为λ的泊松分布,若已知在[0,t)时间内有n个冲击到达,则这n个冲击到达的时间是相互独立的随机变量,服从[0,t)上的均匀分布。 (17) 设tj的密度函数为p(tj),分布函数为F(tj),t1,t2,…,tn,则tj的概率密度函数为 (18) 由于tj服从[0,t)的均匀分布,可得tj的概率密度函数 (19) 则tj的期望为 (20) 其中 (21) 求得tj的期望为 (22) 假设冲击幅值的均值与造成退化量的均值间是比例关系,即μY=aμW,a为常数;某时刻的自然退化量为x2,受到第j-1次冲击时的退化量为xj-1,受到第j次冲击时的退化量为xj。由式(7)可以得到环境OE2中时间的自然退化量x2小于失效阈值H0的可靠度函数 (23) 同理可得时间t的自然退化量x2小于退化量L的可靠度函数 (24) 将式(23)和式(24)代入式(16),则部件在时间t的可靠度函数可写为 (25) 其中,假设tk为当前监测时间,改变环境后的部件剩余寿命概率密度函数为 (26) 因此将式(25)代入式(26),可求得环境改变后部件的剩余寿命概率密度函数。 本文以风力发电机组的关键部件叶片的退化为例进行考虑环境变化的核密度剩余寿命预测建模分析。由文献[23]可知,风力发电机组叶片的自然退化增量Δx1,Δx2,…,Δxk服从形状参数是α=0.542,尺度参数是β=1.147的Gamma分布,采用其退化增量数据作为本文部件的监测数据,退化失效阈值为20 cm,通过蒙特卡洛分析方法对模型进行验证。 根据Shafiee[24]对风力发电机的研究,由蒙特卡洛方法可得冲击到达的速率λ=0.797 7。主要参数如表1所示。 表1 可靠度函数的参数Tab.1 Parameters of the environment reliability function 图2为部件在环境OE1的可靠度函数时间T1=0,100,200,300,400,500,600,700,800时由环境OE1改变为环境OE2时部件的可靠度函数;部件在OE2环境中比在OE1环境中可靠度下降得更快,越早改变环境,部件退化加快,越早失效。 图2 在不同监测时间T1环境改变以及不改变环境的部件的可靠度函数对比Fig.2 Comparison of reliability functions of components with and without environment changes at different monitoring time T1 设时间T1=100,由Gamma分布的数据增量可得当TH=1 024时,部件失效,图3为部件在时间T1=100时改变环境的剩余寿命概率密度函数;表2得出不同监测时间的剩余寿命预测均值,随着部件的不断运行,监测数据会随之增加,剩余寿命概率密度函数左移的越来越快,这是因为部件受到冲击之后,退化加速,平均剩余寿命减小。 表2 T1=100时环境改变的剩余寿命预测值 图3 T1=100时环境改变剩余寿命概率密度函数Fig.3 Probability density function of remaining useful life of environmental change at time T1=100 本文考虑环境改变后的竞争性失效模型中,退化和冲击存在随机相关性,所以有必要研究降低后的突发失效阈值D1、冲击到达的速率λ、冲击幅值的均值μW这些参数对部件可靠度函数和剩余寿命概率密度函数的影响。 如图4(a)所示,考虑不同D1对部件退化的影响,得到D1=1.00,1.50,2.00,2.50,3.00,3.54的部件可靠性曲线和剩余寿命概率密度函数;图4(a)中随着D1的增大,部件的退化曲线右移,退化变慢;图4(b)中则显示为峰值降低,曲线右移,平均剩余寿命增加;在相同的退化条件下,平均剩余寿命降低,表明当部件退化到一定程度,抵抗冲击的能力降低,很小的冲击就会导致部件失效。 图4 不同D1部件的结果图对比Fig.4 Comparison of different results in different D1 如图5所示,考虑不同对部件退化的影响,得到λ=0.797 7,2.393 1,3.988 5的部件可靠性曲线和剩余寿命概率密度函数,随着的增大,环境OE2逐渐恶劣,冲击到达的频率更高,部件退化更快,部件平均失效时间前移。越大的λ值将导致部件在环境OE2中有越高的突发失效概率,导致部件更早失效。 图5 部件在不同λ的结果图对比Fig.5 Comparison of different results in different λ 为进一步对本文剩余寿命预测方法的效果进行评估,表3给出了在不同冲击频率条件下,T1=100时环境改变的部件不同监测时间剩余寿命预测值的比较。由表3可知,相同监测时间,随着λ的增大,部件的剩余寿命预测值减小。 表3 不同λ的剩余寿命预测值Tab.3 Remaining useful life for different λ 如图6所示,考虑冲击幅值的均值μW对部件退化的影响,得到μW=0.25,0.50,1.00的部件可靠性曲线和剩余寿命概率密度函数,随着μW的增大,冲击的幅值越大,环境OE2逐渐恶劣,部件退化更快,部件平均失效时间前移。说明μW对环境OE2中部件可靠性的影响是不可忽略的,越大的μW值意味着每次受到冲击幅值增大,部件运行环境更恶劣,将导致部件在环境OE2中有越高的突发失效概率,导致部件更早失效。 图6 部件在不同μW的结果图Fig.6 Comparison of different results in different μW 表4给出了在不同冲击幅值的均值μW条件下,T1=100时环境改变的部件剩余寿命预测值的比较。由表4可知,相同监测时间,随着μW的增大,部件的剩余寿命预测值减小,随着监测时间的增加,可预测不同μW的部件剩余寿命值。即随着时间的增加,可以预测部件处于不同环境的平均剩余寿命,验证了本模型的有效性。 表4 不同μW的剩余寿命预测值Tab.4 Remaining useful life for different μW 如图7所示,考虑冲击幅值与造成退化量的均值间的比例关系a对部件退化的影响,由图可得比例a越大,图7(a)中可靠度左移,图7(b)中峰值左移,这是由于冲击对部件造成的退化量增大,部件失效越快。 图7 部件在不同a的结果图比较Fig.7 Comparison of different results in different a 本文使用模拟风力发电机齿轮箱的试验台进行验证,如图8所示,该试验台由两部分组成,分别是主试箱和陪试箱,试验台架的中心距为150 mm,试验采用机械杠杆加载,扭矩采用转矩转速传感器进行测量。试验过程中对主试箱和陪试箱中的传感器数据进行监测。 图8 齿轮试验台架Fig.8 Gear test bench 主试箱齿轮安装位置如图9所示,本试验台共安装了11个传感器,其中8个传感器是加速传感器,由于4#传感器的安装位置距离主试箱的轴承近,当传感器接收到齿轮箱发生故障的信号时,此时信号衰减最小,可以很好地表征齿轮箱的状态,故本文选用4#传感器。其余传感如9#和10#为声音传感器,用于监测齿轮箱的声音信号,而11#为温度传感器用于监测齿轮箱的温度。为模拟风机在实际操作过程中环境和负载的随机变化情况,试验加载了八级载荷,从第八级载荷开始预测,在t∈[0,10]h时,齿轮处于啮齿状态;t∈[10,68]h时,特征值不断增大,齿轮进入正常磨损;t∈[68,77]h时,齿轮磨损加剧,在77.17 h发生断齿,此时齿轮的故障阈值为y=77.325 mm/s2。由于齿轮在68 h之后磨损突然加剧,建模为随机冲击导致的退化加快。在进行数据采样时,每隔9 min记录一次采样数据,每次采样时长为60 s,采样频率为25.6 kHz。 图9 主箱齿轮安装位置Fig.9 Location of gear in the main box 在数据采集过程中,由于实际应用中存在着大量未知干扰,获取的实际数据中也不可避免叠加了很多噪声,本文使用均方幅值的方法,可以对原始振动数据进行去噪处理的同时并进行特征提取,从而能更好地表征齿轮退化状态,如图10所示。采样信号的均方幅值计算为 图10 滤除噪声特征提取后齿轮的退化示意图Fig.10 Schematic diagram of gear degradation after noise filtering and feature extraction (27) 式中:N为采样点数;yM为第M个振动信号的幅值。 如图11所示,*为齿轮的真实剩余寿命,°为本文的模型。由图11可知,当部件不断运行时,剩余寿命概率密度函数左移的速度越来越快,这表明当部件受到冲击之后,退化加速,平均剩余寿命减小,由此验证了本文所提出模型的合理性与有效性。 图11 环境改变后齿轮得剩余寿命概率密度函数Fig.11 Probability density function of remaining Useful Life of gears after environmental changes 表5中对不同时刻的齿轮剩余寿命的进行比较,在tk=68 h后,冲击出现时,由于监测数据集不够,均方根误差(root mean square error,RMSE)会偏大,随着数据的增多,本模型的准确性也逐渐提高。 表5 不同监测时间下的齿轮箱剩余寿命预测值 本文考虑部件在实际运行中,外界环境会发生改变,将恶劣环境对部件的影响建模为部件受到的随机冲击,考虑窗宽对核密度估计的影响,从数据本身出发使用自适应核密度估计得到自然退化模型;由于环境改变后部件受到冲击产生的退化与连续自然退化过程具有随机相关性,当退化到一定程度后会降低突发失效阈值,因此在环境改变后考虑变失效阈值,引入核密度估计建立考虑冲击与连续自然退化过程之间随机相关的模型,建立了考虑环境随机冲击影响的剩余寿命预测模型,预测部件的平均剩余寿命。最后以风电机组为研究对象,验证了冲击的到达率和使突发失效阈值改变的退化量均影响剩余寿命预测值,即环境改变后,环境的恶劣程度对部件的剩余寿命影响无法忽视。 本文研究仅考虑单个部件在环境改变后的剩余寿命预测,没有考虑到更为复杂的多部件的情况,多部件系统中各部件之间的随机相关性也会影响剩余寿命的变化,因此考虑多部件系统存在的随机相关性,在运行环境改变后的剩余寿命预测值得进一步研究。1.1 部件自然退化过程
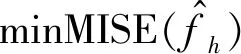
1.2 环境改变冲击对自然退化的随机相关性影响
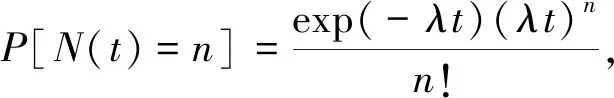
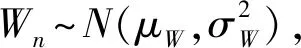
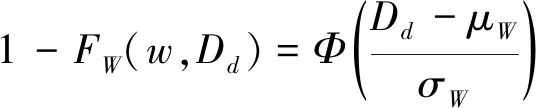
1.3 可靠度函数建立
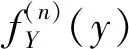
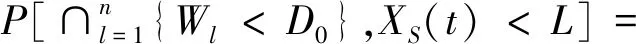
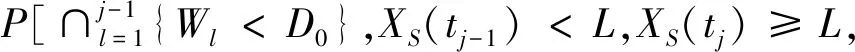
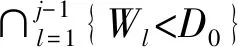
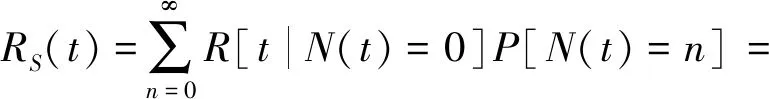
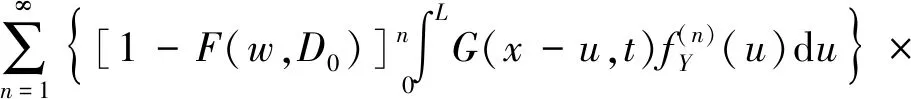
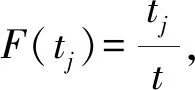
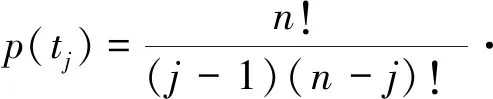
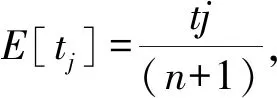
2 数值试验分析

2.1 可靠度函数
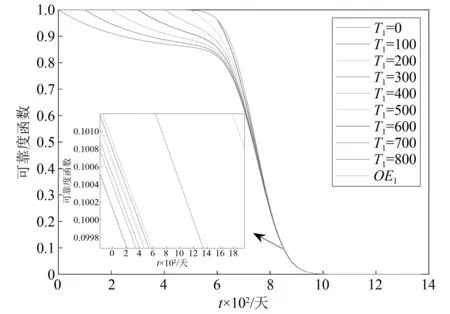
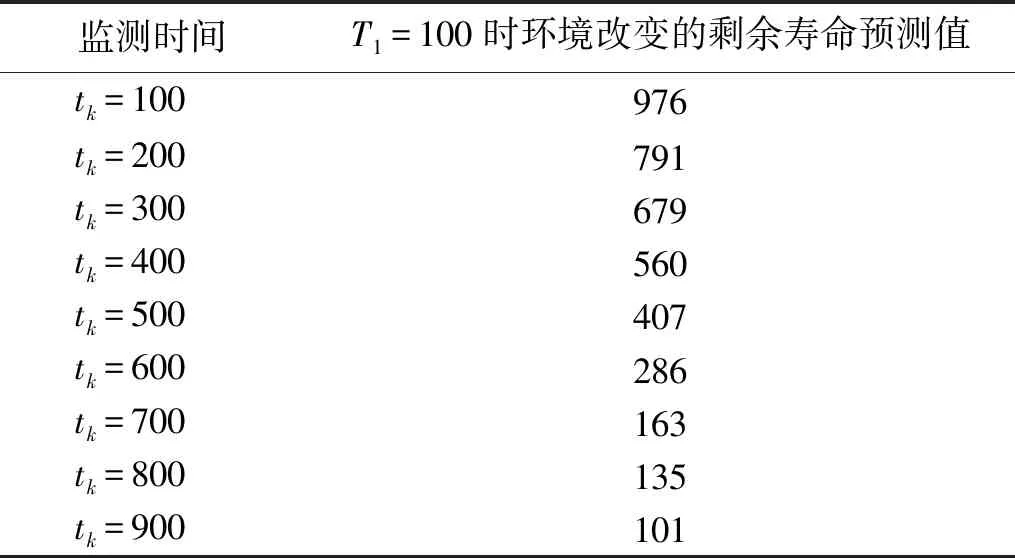
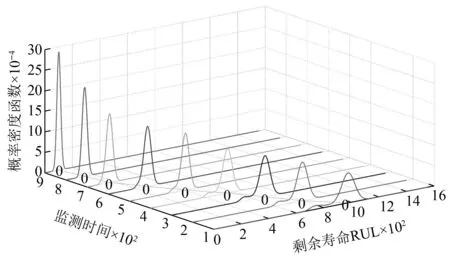
2.2 剩余寿命预测
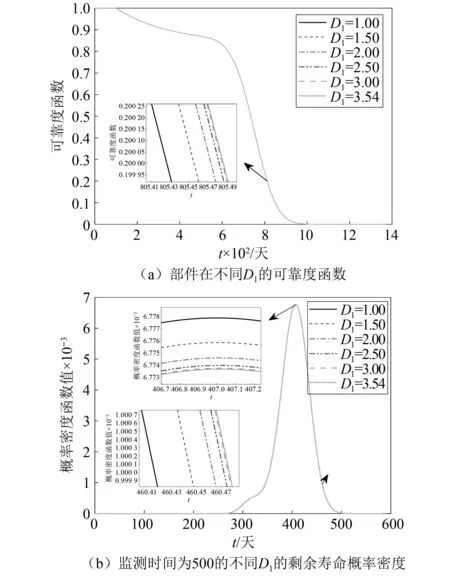
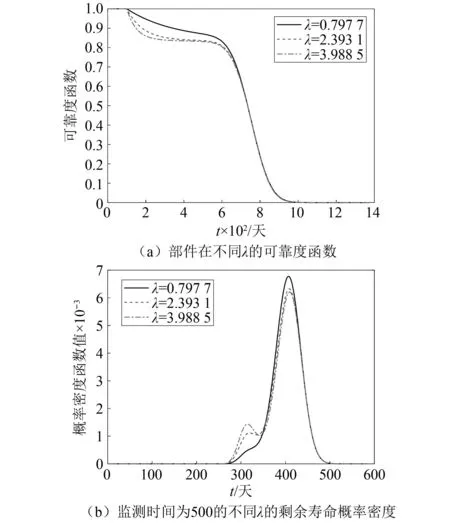
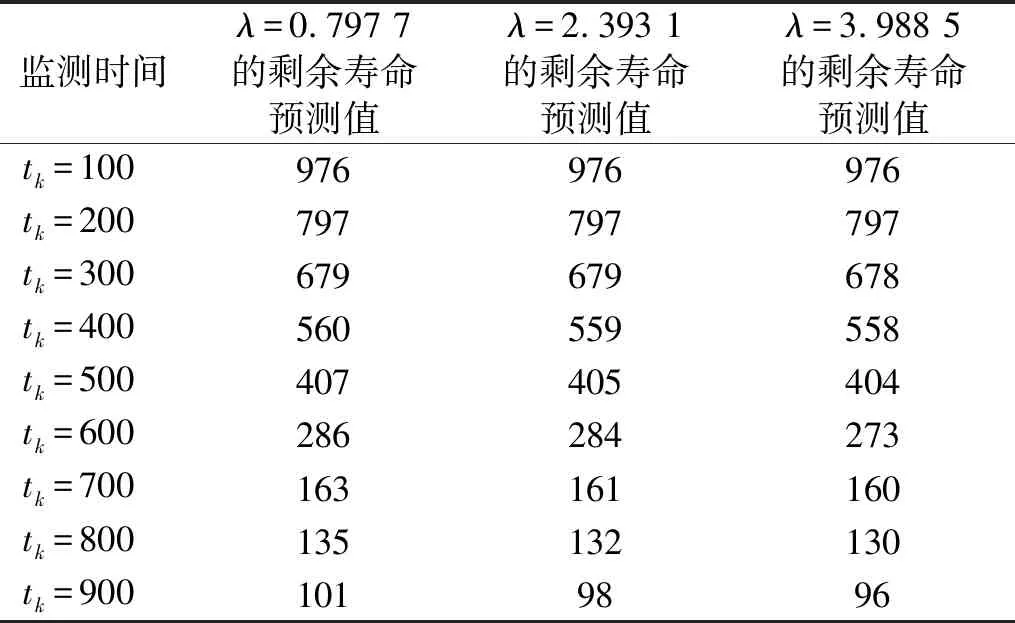
2.3 敏感度分析
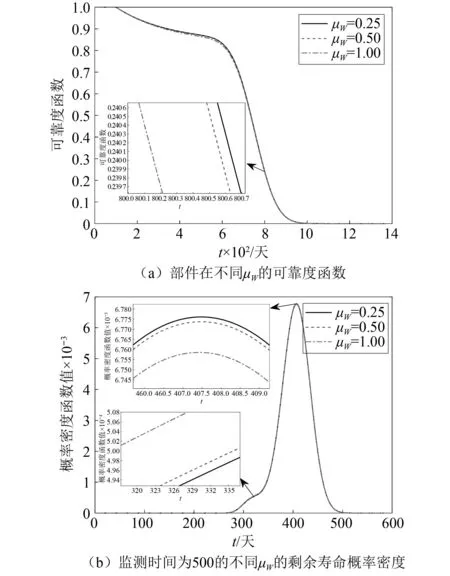
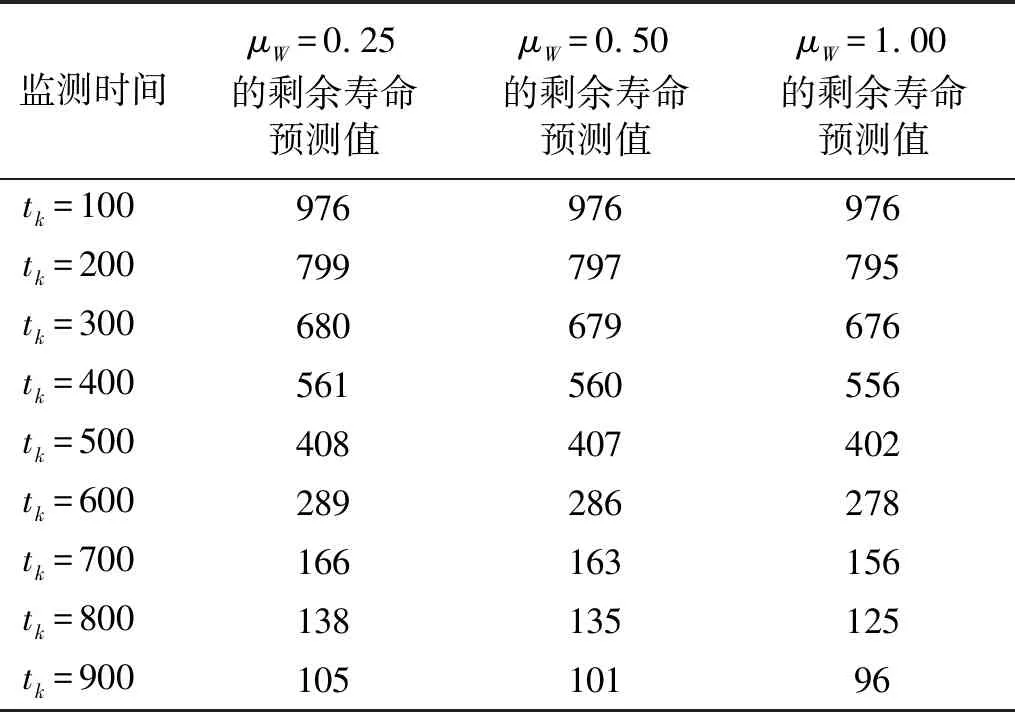
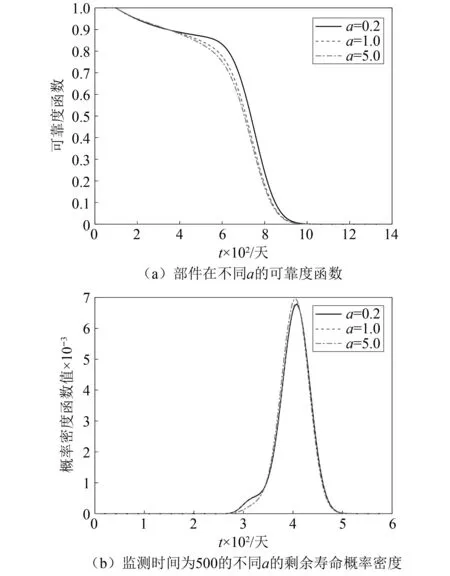
3 实例分析


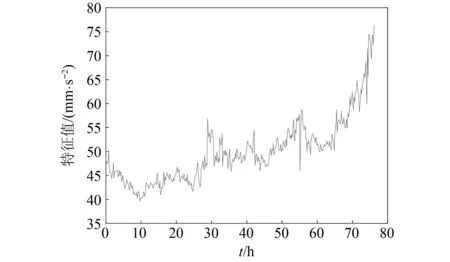
3.1 剩余寿命预测
4 结 论

