火箭捆绑机构热力耦合模型修正与虚拟验证方法

贺 揆, 张 薇, 李长龙, 裴长浩

(1. 北京航空航天大学 可靠性与系统工程学院,北京 100191;2. 北京宇航系统工程研究所,北京 100076)

在重型运载火箭的飞行过程中,球头-球窝式捆绑机构为了适应芯级与助推器之间的相对弹性变形会发生转动摩擦,大吨位载荷作用下的转动摩擦会产生大量热量导致捆绑机构温度过高,从而严重影响整体强度甚至导致结构失效[1],因此需要精确的热力耦合有限元分析来辅助结构设计以及结构优化。

对于热力耦合有限元建模,袁水林等[2]采用ANSYS软件建立了某型号球头-球窝式捆绑机构的有限元模型并进行了摩擦热分析,研究了摩擦系数对捆绑机构温度分布的影响。除进行热力耦合有限元分析以及研究各参数对结果的影响外,张薇等[3]还建立了摩擦热理论模型,并将理论分析结果与有限元仿真结果相互验证。

但是,考虑到热力耦合这种复杂的物理过程以及有限元建模中存在的不确定性,有限元分析的结果与实际情况不可避免地存在着差异。于是为了减小这一差异,提出使用模型修正技术,基于已有的试验观测值,通过调整有限元模型的材料参数、几何特征等输入参数,来减小仿真结果与试验数据的差异,从而提高有限元模型的计算精度[4]。传统的模型修正主要针对结构动力学的有限元模型,一般将弹性模量、密度等材料参数作为输入参数,输出特征则仅考虑结构的固有频率或者频响函数(frequency response function, FRF)[5]。然而,在考虑热环境的有限元模型修正中,热传导系数、比热容等热力学参数由于存在不确定性也需要作为待修正参数,同时结构温度则需考虑作为输出特征。张保强等[6]针对热传导模型确认挑战问题,使用贝叶斯方法对热传导系数以及体热容等参数进行了修正。而对于更复杂的飞行器结构热力耦合模型修正问题,现有的研究主要以优化的思想来实现,通常先构造目标函数、确定设计变量,然后通过遗传算法[7]、粒子群算法[8-9]以及拟牛顿法[10-11]等优化算法进行求解。虽然上述优化类算法在减小观测量偏差上确实能起到一定效果,但输入参数还是难以被修正到精确值[12]。除直接使用优化算法以外,何成等[13]还提出了一种分层修正策略,并推导了不确定性参数均值及其协方差矩阵的迭代修正方程。目前关于热力耦合模型修正的方法还比较单一,所以有必要尝试更多其他类型的模型修正算法,来解决更复杂、高维的热力耦合模型修正问题。

模型修正需要试验观测数据作为依据,然而在很多实际工程应用中,试验数据是比较稀缺的。比如火箭捆绑机构,其实际工作环境中载荷巨大、工况严峻,进行地面模拟试验成本高、难度大,这也就造成运载火箭新型号的设计周期长、设计效率低。因此,如何充分利用前期型号的已有试验数据来验证甚至修正在研新型号结构的有限元模型就成为了关键的技术难题。

为解决上述难题,本文提出一种热力耦合模型修正与虚拟验证方法,并将以上方法用于修正某在研型号火箭捆绑机构的热力耦合有限元模型。首先,基于某前期型号的试验数据,使用基于距离判别的贝叶斯修正方法对前期型号有限元模型进行模型修正;然后,通过修正后的前期型号有限元模型标定通用化的摩擦热理论模型,建立温度与结构几何尺寸、材料参数以及工况参数的关系公式;最后,将在研型号的参数代入通用理论模型得到理论温度值,并将理论值作为依据进行新一轮模型修正,从而得到精确的在研型号有限元模型。

1 模型修正算法

这部分介绍本文所采用的模型修正方法,将用于修正后续热力耦合有限元模型。目前常用的模型修正方法包括优化类修正、协方差修正、区间类修正以及贝叶斯修正。优化类修正主要基于模型输入输出参数间的梯度信息,为传统的确定性修正算法;协方差与区间修正除参数均值外还考虑了参数的方差以及范围信息,涉及了模型修正中的不确定性分析;贝叶斯修正是一类典型的随机修正方法,利用待修正参数的先验分布与后验分布描述修正前后的参数随机特征。上述各类方法的详细比较与特征可见Broggi等[14-17]研究。本文将使用贝叶斯修正算法,一方面因为该方法适用于解决高维问题,往往能够极大缩减预测值与实际值的误差,同时还具有很高的计算效率;另一方面,热力耦合模型修正问题面临输入参数不确定性差异巨大且相互耦合等难点,贝叶斯修正方法得到的输入参数后验分布有助于在统计意义下估计最优解。

同时,热力耦合的单次有限元分析十分耗时,而模型修正算法又需要大量地调用有限元模型,因此本文将通过二次多项式响应面的方法建立代理模型,从而尽可能减少计算成本。

1.1 贝叶斯修正框架

本文所采用的贝叶斯修正框架将结合近似贝叶斯计算方法(approximate Bayesian computation, ABC)以及过渡马尔科夫链蒙特卡洛算法(transitional Markov chain Monte Carlo, TMCMC),该框架的核心为概率统计理论中的贝叶斯原理,表示为

(1)

式中:x为输入参数,即待修正参数;Yexp为试验观测样本;P(x)为待修正参数的先验分布;P(x|Yexp)为待修正参数后验分布,也就是依据观测值修正得到的结果;P(Yexp)为归一化参数,本质是观测数据的概率积分,其确保后验分布概率累计积分为1;PL(Yexp|x)为似然函数,本质是现有试验观测数据基于输入参数样本的条件概率。

贝叶斯修正框架中的一大难题就是归一化参数P(Yexp)难以计算,因此提出使用TMCMC算法,通过迭代过程,从一系列中间概率密度函数采样去逐渐逼近后验分布。第j代中间概率密度函数可表示为

Pj∝PL(Yexp|x)βjP(x)

(2)

式中,βj为似然函数的权重指数,其中,j=1,2,…,m,m为总迭代次数,在迭代开始时β0=0,式(2)右边即为先验分布,后随着迭代逐渐逼近βm=1,等式右边也就变为后验分布。每次迭代步中βj都根据上一个迭代步中的采样样本计算得到。TMCMC算法中,马尔科夫链以及Metropolis-Hastings采样方法不断地从具有高似然值的样本中传播出新的样本,从而实现了从复杂的后验分布采样。该方法的更多细节可见Ching等[18]研究。

贝叶斯修正框架中的第二个难点就是似然函数PL(Yexp|x)的计算,似然函数依照定义可写为

(3)

由式(3)可以看到,似然函数的计算需要对每一个试验样本估计出基于待修正参数的条件概率,而每一次估计都需要大量地调用数值模型,因此计算成本极高。为解决这个难题,提出使用ABC方法来简化似然函数,表示为

(4)

式中:σ为宽度系数,一般可取为[10-3,10-1][19];d为统计学距离指标,用来衡量预测样本与观测样本的差异。本文选用欧氏距离作为距离度量指标,其表达式为[20]

(5)

1.2 二次多项式响应面

多项式响应面是最常用的代理模型之一,它在参数空间内构造输入输出间的多项式函数关系,从而逼近真实有限元模型,原理简单、直接。对于热力耦合有限元模型,输出为温度、应力等物理量,输入则为力学性能参数、热性能参数等等,相应的输入输出关系也就往往呈现单峰值、低阶非线性、输入参数变化范围小等特点,因此本文使用二次多项式响应面来构建热力耦合有限元分析的代理模型。对于第个输出特征,基于二次多项式的代理模型可构造为

(6)

式中,β为模型的待定系数,通过最小二乘法估计得到。

在代理模型构建完成后,还需对其精度进行验证。于是本文选择均方根误差(root mean square error, RMSE)作为代理模型的检验指标,表达式为

(7)

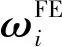
2 虚拟验证方法

虚拟验证方法重点解决新型号捆绑机构设计中没有任何试验数据的情况,利用已有的捆绑机构摩擦热试验历史数据以及热力耦合分析的通用理论公式,建立新旧型号之间的关联,从而验证并修正在研新型号的有限元模型。

2.1 虚拟验证框架

对于一个系列的火箭捆绑机构,其结构外形、接触方式以及运动形式基本一致,不同的型号仅在几何尺寸、工况参数以及材料参数上存在一定范围内的差异。因此考虑建立通用化的摩擦热理论模型,使得理论计算结果与有限元仿真结果在不同输入参数下仍能保持一致。结合有限元模型、模型修正技术以及通用化理论模型,可以构造出虚拟验证的基本原理框架,如图1所示。

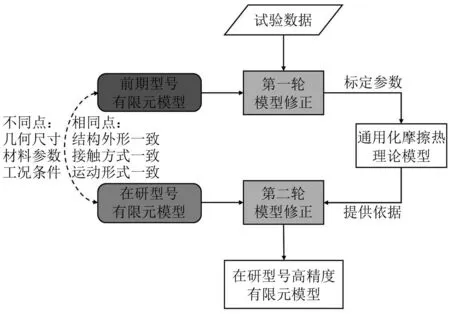
图1 虚拟验证框架Fig.1 Virtual verification framework

在该虚拟验证框架中:①需要对前期、在研两型号的捆绑机构进行初步的有限元建模,其中部分输入参数因认知不完全存在不确定性;②以前期型号的摩擦热试验数据为观测值,使用1.1节介绍的贝叶斯修正算法对前期型号有限元模型开展第一轮模型修正;③建立通用化理论模型,利用修正后的前期有限元模型的仿真结果去标定理论模型的待定系数;④将在研型号的输入参数代入理论模型,将理论计算结果作为观测值,在初步验证有限元仿真结果合理后,对在研型号有限元模型进行第二轮模型修正;⑤得到高精度的在研型号有限元模型,从而辅助在研型号后续的设计研制工作。

2.2 通用化理论模型

本文所使用的通用化理论模型为球头-球窝式捆绑机构摩擦热计算模型,下面将列出部分重要的计算公式及推导过程。首先,建立球头-球窝结构的Hertz接触模型,具体外形如图2所示,计算得到球头-球窝接触形式的啮合深度δ,表示为

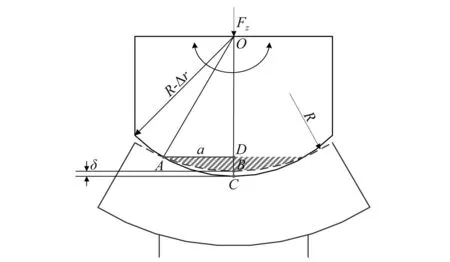
图2 球头-球窝Hertz接触模型Fig.2 Hertz contact model of ball-and-socket mechanism

(8)

式中:Fz为等效集中载荷; Δr为球头与球窝的半径差;E为材料弹性模量。同时,计算得到等效接触面的横向长度a,即图2中AD段的长度,可写为

(9)

于是,接触面上的平均接触压力可以写为

(10)

式中,λ为接触面积修正系数。在此基础上,假设等效温升区域如图2中阴影部分,根据热力学定律以及集中参数法可以推导出该区域的温度变化公式,表示为

(11)

式中:α为等效接触区域质量修正系数;γ为热散失项修正系数;b为AB段长度;θ为球头转动角度;f为转动频率;T0为初始温度;ρ为材料密度;h0为BD段长度;CV为材料比热容。

通用化理论模型中包含3个待定系数,分别为λ、α以及γ。因此在构建模型时,需要以第一轮修正后的有限元模型作为依据去标定这三个参数。本文采用分部策略,先通过有限元仿真的接触压力计算结果去标定式(10)中的λ,然后再通过温度仿真结果去标定式(11)中的α与γ。

3 数值算例

本章将使用前文中提到的方法建立某型号运载火箭捆绑机构的精确热力耦合有限元模型。

3.1 捆绑机构热力耦合有限元模型建立

球头球窝式捆绑机构的外形如图2所示,球接触面的标称半径为75 mm,存在半径差Δr,即球头球面半径为(75-Δr)mm。为模拟捆绑机构在实际工作情况中的转动摩擦情况,在有限元仿真中令球窝固定,令球头绕球心在XZ平面上进行周期性的往复摆动,同时均布载荷持续作用在球头上表面。仿真使用热力耦合分析,单元类型设置为C3D8RT。网格尺寸整体设置为5 mm,接触面区域加密至2 mm。通过演示算例可以看到该结构的运动及传热效果,截取三个时刻的仿真结果如图3所示。

图3 演示算例仿真结果Fig.3 Simulation results of demonstration case

3.2 第一轮模型修正

第一轮模型修正的对象为某前期型号的热力耦合有限元模型,其外形与3.1节中的建模一致。对于该型号,半径差设置为0.5 mm,接触面摩擦系数0.15,球头转动频率2 Hz,最大转角2°,外载荷等效为集中力,大小2×106N,初始温度20 ℃。该型号捆绑机构的材料为合金结构钢30CrMnSiNi2A。

首先,对待修正参数进行选择。有限元模型的输入参数包括:材料力学性能参数、材料热学性能参数以及热环境参数,这些参数在一定程度上都具有不确定性,在建立有限元模型时难以确定其数值。参考文献[13],弹性模量以及导热率随温度的改变会发生明显变化,因此有必要先单独对这两个参数进行处理。分别取温度为20 ℃以及500 ℃时对应的弹性模量以及导热率,分别记为E20,E500,k20和k500, 并将这两个参数的温变特性用一次函数来描述,得到表达式为

(12)

为证明用一次函数描述温变特性的合理性,针对高强度钢30CrMnSiNi2A,通过JMat Pro数据库软件,计算一组不同温度下的弹性模量以及导热率作为参考值,绘制如图4与图5所示。取E20,E500,k20和k500构造一次函数也绘制在图4与图5中,现考察该拟合函数对参考数据点的拟合精度。参考式(7),计算一次函数上数值相对于对应参考数值的百分比形式的RMSE,弹性模量的拟合RMSE为0.59%,导热率的为0.12%,因此认为使用一次函数来拟合温变特性是具有足够高精度的。

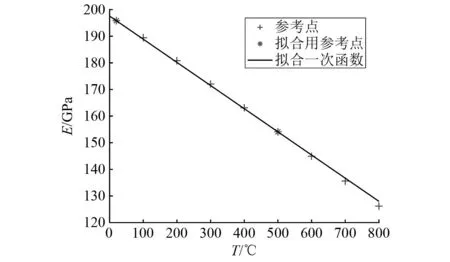
图4 弹性模量温变模型Fig.4 The temperature variation model of elasticity modulus

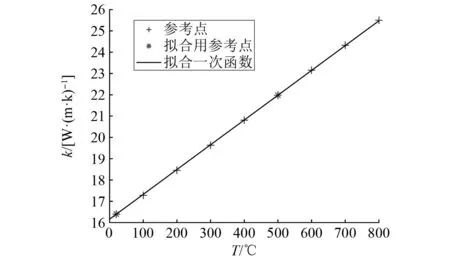
图5 导热率温变模型Fig.5 The temperature variation model of thermal conductivity

除此以外,材料参数中的密度、比热容与线膨胀系数以及描述结构散热情况的表面换热系数与辐射率都存在不确定性,因此也被选为待修正参数。最终,9个待修正参数及其变化范围列在表1所示。

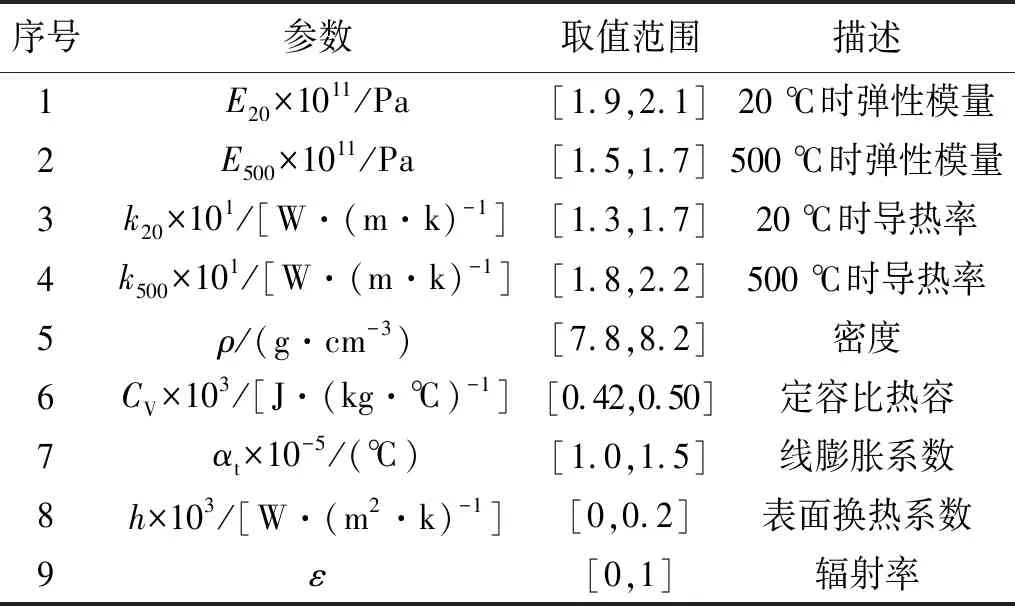
表1 第一轮模型修正的不确定参数

下一步,对输出特征进行选择。对于热力耦合分析,关注的输出主要为应力分布以及结构升温情况。在前期型号的摩擦热试验中,观测量由一系列布在结构外部的传感器测得,包括实时的应力与温度。在模型修正的输出特征选择上,应保证与试验观测量一致。因此,选择球头、球窝上4个测点的温度及应力值共8个物理量作为输出特征,记为Si与Ti,i=1,2,3,4。4个测点的具体位置如图6所示。

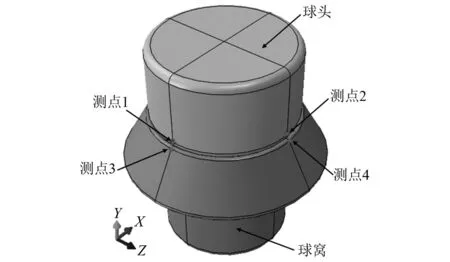
图6 测点位置参考Fig.6 Location reference of measurement points

在模型修正中需大量调用有限元分析,因此对上述输入输出构建代理模型。进行试验设计获取多组有限元仿真结果,对上述9个待修正参数设计9因素3水平正交表,共27组试验,记为L27(39)。低、中、高三个水平分别对应着输入参数变化范围的下界、中点以及上界。于是用这27组数据计算式中的待定系数β,从而得到前期型号有限元模型的二次多项式响应面代理模型。使用拉丁超立方采样从取值范围内随机得到5组验证样本,分别代入有限元模型与代理模型得到输出响应。对5组试验样本的有限元仿真值与代理模型拟合值进行比较,并依照式计算对于每个输出特征的RMSE,计算如表2所示。可以看到,8个特征中均方根误差最高达到3.00%,平均误差为1.59%,精度能满足要求,代理模型可用于后续模型修正。

表2 代理模型关于8个输出特征的均方根误差

代理模型构建完毕后,根据1.1节中介绍的贝叶斯修正框架进行模型修正。设置TMCMC样本数为2 000,经历7次迭代后得到各输入参数的后验分布如图7所示。图7中的9幅图为每个待修正参数2 000个样本的后验分布柱状图,区间对应的值越大,说明该区间上的样本点越多。可以发现,经过修正后的后验分布非常集中,绝大多数样本点都聚集在极小的区间内,因此各输入参数的修正值可以简单地取为相应区间的中点,即图7中的“*”号标记点处,具体数值如表3所示。

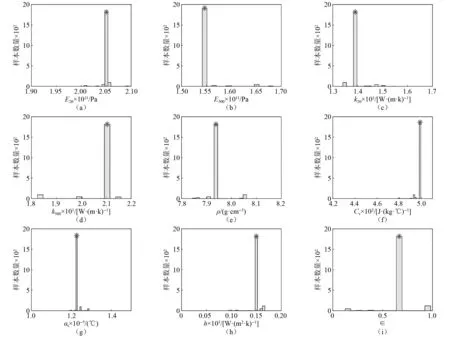
图7 第一轮模型修正后验分布柱状图Fig.7 Posterior distributions after first round calibration

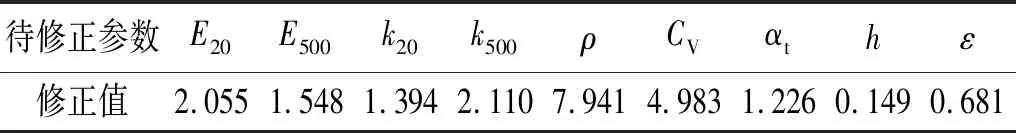
表3 第一轮模型修正输入参数修正值Tab.3 Updated input parameters after first round calibration

将上述输入参数的修正值再代入有限元模型中,验证各输出特征的仿真值与试验值是否足够接近。计算得到输出特征的试验值、仿真值以及误差列在表4中,其中应力单位为MPa,温度单位为℃。由表4可得,输出特征中最大的预测误差仅为2.45%,各输出特征的平均误差更是只有1.13%,表明修正后的有限元模型已经十分接近于实际情况。

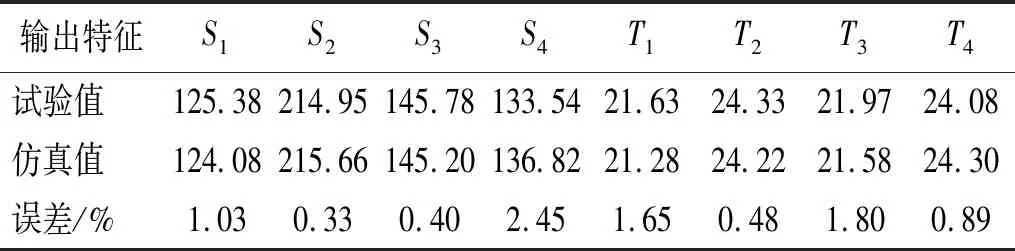
表4 第一轮修正输出特征及误差

对修正后的输入参数进行有限元仿真,得到结构末时刻的温度场云图如图8所示。有限元仿真可以得到结构整体的温度分布以及最大温度,这些数据在实际试验中难以全面测量,但模型修正保证了这些仿真值的正确性,使其能够在后续用于理论模型标定。

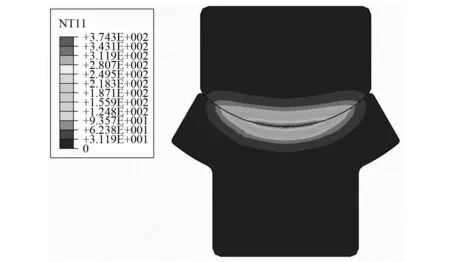
图8 第一轮修正后末时刻温度云图Fig.8 Temperature nephogram at final moment after first round calibration

3.3 理论模型标定

基于第一轮修正后的有限元模型,对通用化理论模型进行标定。首先,通过接触压力标定式(10)中的接触面积修正系数λ。式(10)中计算得到的是理论接触面上的平均接触压力,而实际上,在存在半径差且不考虑弹性形变时,球头-球窝接触为点接触,因此不妨就直接使用有限元仿真得到的球头接触面中心最大接触压力来进行标定。利用3.2节中的结果,最终标定接触面积修正系数λ=0.426。

同理,通过球头顶点处的温度仿真值,标定式(11)中的等效接触区域质量修正系数α以及热散失项修正系数γ。由于待标定系数有两个,因此需要构造大于等于2组的仿真结果来作为标定的依据。在不改变结构外形以及材料的基础上,考虑只改变转动频率来构造多组数据,并通过Levenberg-Marquardt方法减小仿真值与理论值的差异,将得到的最优解作为α以及γ的标定值。最终标定等效接触区域质量修正系数α=0.104,热散失项修正系数γ=0.043。将上述标定数值代入理论模型,得到不同转动频率下温度变化的理论计算值与仿真值,如图9所示。可以看到,理论计算值与仿真值差异较小,因此可以认为该理论模型能代表修正后有限元模型的计算结果。

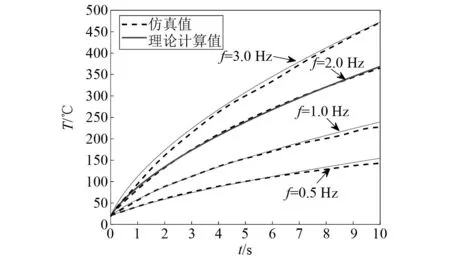
图9 不同转动频率下仿真与理论温度值对比Fig.9 Comparison of temperatures calculated by FEM and theoretical model under different rotational frequencies

3.4 第二轮模型修正

第二轮模型修正的对象是在研新型号捆绑机构,其有限元模型基本与前期型号一致,但材料改变为沉淀硬化不锈钢PH13-8Mo,且其他个别参数更改为:半径差Δr=0.7 mm,球头转动频率0.8 Hz,外载荷上升至2.4×106N。由于在研型号不具备试验数据,因此将理论模型计算值作为观测值对在研型号有限元模型进行验证及修正。

类似3.2节中的步骤,先确定模型的输入参数,根据在研型号的材料PH13-8Mo,总结各输入参数如表5所示。其中,由于弹性模量、密度以及比热容是理论模型的输入参数,因此不将其考虑为待修正参数,而直接认为是确定值。所以,第二轮修正的待修正参数分别为20 ℃及500 ℃时的导热率、线膨胀系数、表面换热系数以及辐射率5个物理量。

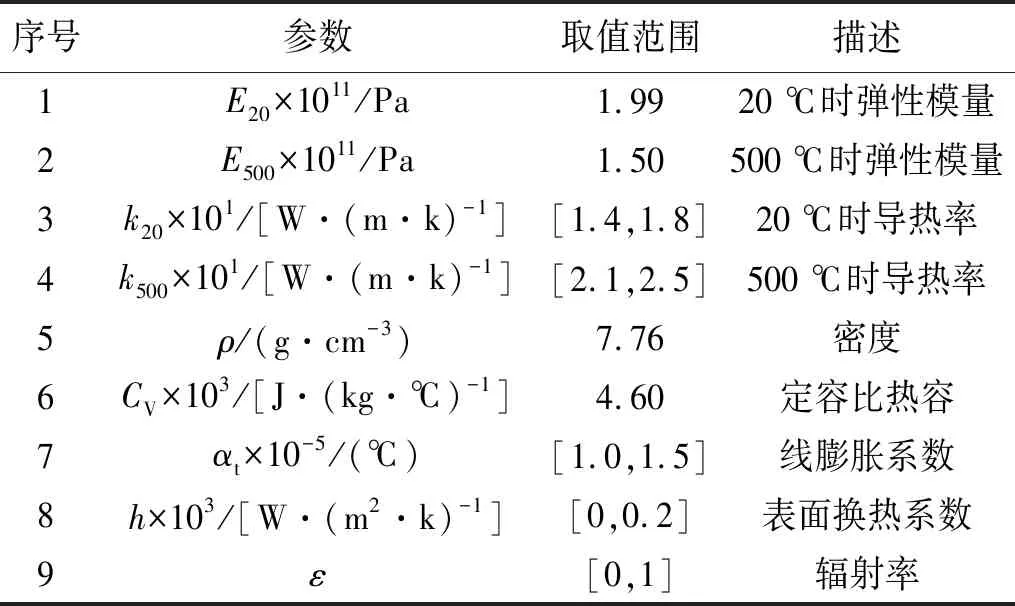
表5 在研型号模型输入参数Tab.5 Input parameters of new developing model

对于输出特征,由于理论模型只能计算出球头顶点的温度值,因此取该位置上t=2 s,4 s, 6 s, 8 s, 10 s共5个时刻的温度作为输出特征。根据已确定的输入输出,进行试验设计,并构建在研型号的代理模型。对5个待修正参数建立5因素3水平的正交表,共18组试验,记为L18(35)。依照正交表进行18组有限元仿真,并根据仿真结果建立二次多项式响应面代理模型。同样地,再获得5组验证样本,并计算代理模型对于输出特征的RMSE如表6所示,平均RMSE仅为0.68%,代理模型误差较小,可用于后续模型修正。

表6 代理模型关于5个时刻温度的均方根误差

将18组试验得到的末时刻球头顶点温度值的分布绘制如图10所示,可以看到温度的变化范围为[271.50, 308.58]。将相应输入参数代入理论模型后,得到理论计算值为277.12 ℃,落在试验样本的输出变化区间内。由此,可以初步说明在研型号有限元仿真结果具有一定合理性,但仍需模型修正过程进一步提高模型精度。

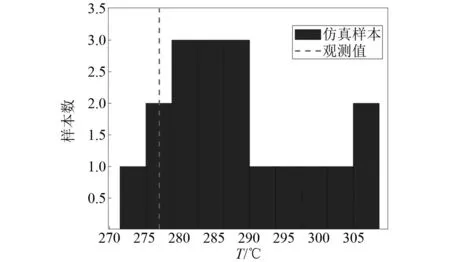
图10 仿真样本分布图Fig.10 Distribution of simulation samples

进一步地,依照理论计算值对在研型号有限元模型进行修正,在TMCMC算法中设置样本数为2 000,经过6次迭代,得到后验分布如图11所示。由图11可知,第二次模型修正得到的参数取值区间得到了明显的缩减,但与第一轮修正的结果不同,修正后样本在区间内分布得相对分散。于是,在确定修正值时,使用核密度估计方法拟合出各参数后验分布的概率密度函数,并将概率密度函数最大值对应的横坐标作为修正值, 图11中的星形标记点处,具体数值如表7所示。

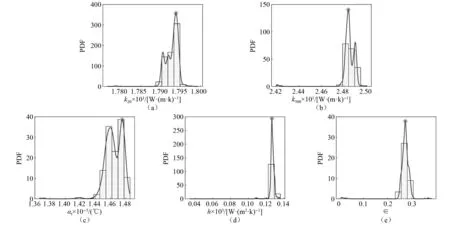
图11 第二轮模型修正后验分布柱状图Fig.11 Posterior distributions after second round calibration

表7 第二轮修正输入参数修正值

将该组修正值代入有限元模型,计算得到结构温度云图如图12所示。各输出特征的理论计算值以及有限元仿真值分别列在表8,可以看到平均误差为4.94%。由图12、表8可知,第二轮模型修正依然能显著减小在研模型有限元模型与理论模型的差距,而此时的有限元仿真结果经过虚拟验证也更具可靠性。

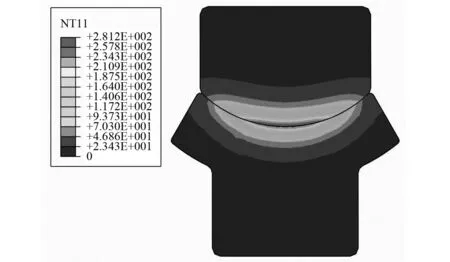
图12 第二轮修正后末时刻温度云图Fig.12 Temperature nephogram at final moment after first round calibration

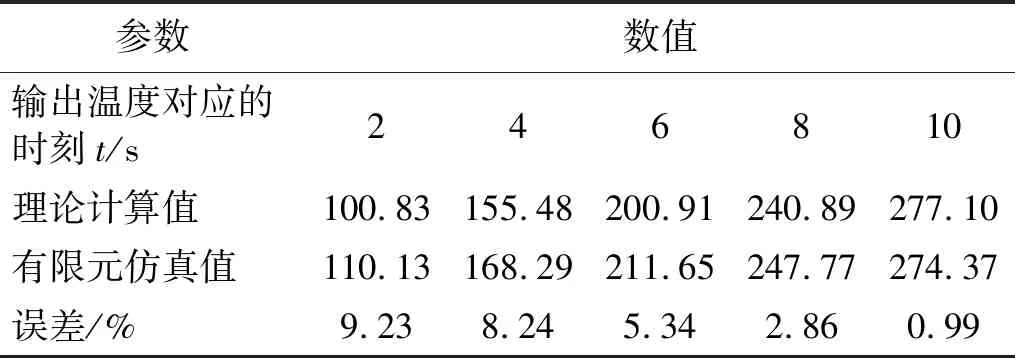
表8 第二轮修正输出特征及误差

4 结 论

针对缺少试验数据的在研新型号火箭捆绑机构有限元模型修正,本文提出考虑建模不确定性的热力耦合模型修正方法以及基于通用化理论模型的虚拟验证方法,充分利用前期型号的已有试验数据,验证并修正了在研新型号热力耦合有限元模型。得到结论如下:

(1) 本文通过贝叶斯修正框架对前期型号的热力耦合有限元模型进行了模型修正,最终修正后的仿真结果与实际试验值相差小,证明了前期型号有限元模型与实际情况贴合较好,仿真值具有较高精度。

(2) 标定了通用化热力耦合理论模型,理论计算值能反映修正后有限元模型的仿真结果。对于同一系列不同型号的捆绑机构,该理论模型计算值也具有较高的通用性参考价值。

(3) 基于通用化理论模型,验证并修正了在研新型号的热力耦合有限元模型,在不具备试验数据的情况下,保证了仿真结果的精度,对后续的型号设计、结构优化等环节提供了基础。