玄武岩纤维增强聚合物筋混凝土循环拉拔试验及预测模型

柴松华，杜红秀，吴凯，黄锐，周驰词*

（1.运城职业技术大学建筑工程学院，山西 运城 044000；2.太原理工大学土木工程学院，太原 030024；3.四川省公路规划勘察设计研究院有限公司，成都， 610041）

0 前言

在服役期间，混凝土结构不可避免地受到交通、风荷载、温度、地震等循环荷载的影响。循环荷载下，钢筋与混凝土黏结性能是影响结构抗震及抗疲劳特性的关键因素［1-3］。高性能混凝土在早期易出现裂缝，尤其在沿海地区，混凝土内部的钢筋面临着腐蚀问题，从而影响其安全性和耐久性。BFRP筋是一种新型材料，在混凝土结构中能替代传统钢筋［4］。BFRP筋具有优异的物理力学性能［5］，如轻质、高弹性模量、高抗拉强度和抗疲劳性能等。目前，已有研究对静荷载作用下BFRP筋与混凝土的黏结应力-滑移关系［6］进行了分析，显示黏结强度与混凝土强度成正比，与BFRP筋直径成反比，建立了BFRP筋与混凝土黏结应力-滑移关系的预测模型。然而，在循环荷载作用下，筋材与混凝土的黏结性能与静载作用下不同［7］。因此，有必要进一步探究BFRP筋与混凝土之间的动态黏结行为。

在强烈的地震活动中，循环荷载会导致钢筋与混凝土黏结性能发生劣化［8］，而混凝土结构的滞回性能又高度依赖于钢筋与混凝土之间的黏结特性［9］。目前，混凝土与钢筋［10］、玻璃钢筋［11］、碳FRP筋［12］和玻璃钢片材［13］在循环荷载下的黏结性能已有研究，但BFRP筋与混凝土动力黏结性能研究仍然缺乏。因此，有必要对循环荷载作用下BFRP筋与混凝土的黏结性能进行探索。为此，本文开展循环拉拔试验，研究不同直径BFRP筋与混凝土的黏结-滑移曲线，重点分析黏结强度、滑移量、滞回面积受循环荷载次数的影响；同时基于试验结果和既有预测模型，提出了适用于BFRP筋与混凝土黏结行为的计算公式。研究成果可为BFRP筋混凝土抗震及疲劳特性研究提供试验和理论支撑。

1 实验部分

1.1 主要原料

普通硅酸盐水泥的P-II 42.5，粒度为375 m2/kg，湖南鑫鼎力新材料科技有限公司；

粗骨料采用石灰石碎石，粒径为4.75～20 mm，表观密度为2 660 kg/m3；

细骨料采用细度模数1.93，最大粒径为1.5 mm的天然河砂；

聚羧酸基液体高效减水剂，减水率为23 %～30 %，山西佳维新材料股份有限公司。

试验设计了混凝土配合比（水∶水泥∶细骨料∶粗骨料∶高效减水剂=168∶420∶673∶1 176∶1.26），混凝土28 d立方抗压强度为43.60 MPa。试验采用直径12 mm和14 mm的BFRP筋，由山西晋投玄武岩纤维有限公司提供，纤维体积分数为75 %，表面涂层为乙烯酯树脂。破坏前，BFRP筋的应力-应变关系为线性，物理力学指标见表1。

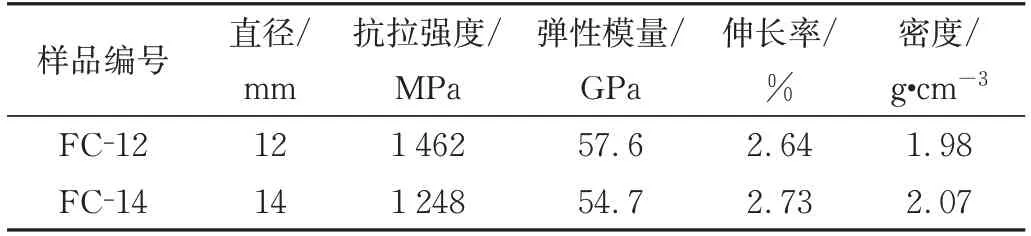
表1 BFRP筋的基本力学指标Tab.1 Basic mechanical indicators of BFRP reinforcement

1.2 主要设备及仪器

伺服液压试验机，MTS 322，电机功率为150 W，最大试验力为5～100 kN，位移分辨率为0.01 mm，调速范围为1～500 mm/min，山东万辰有限公司。

1.3 样品制备

混凝土试件尺寸为150 mm×150 mm×150 mm，与BFRP筋的黏结长度为70 mm，位于试件中部。为保证应力的均匀传递，BFRP筋两端头（40 mm）采用管径18 mm的PVC管进行套护，如图1所示。混凝土分2层布置BFRP筋层。为防止混凝土浇筑时出现空洞，使浆体充分包裹BFRP筋，采用振动棒对混凝土拌合物完全捣实。最后，将浇筑好的试件置于相对湿度为95 %和温度为20 ℃的养护环境中，养护28 d。

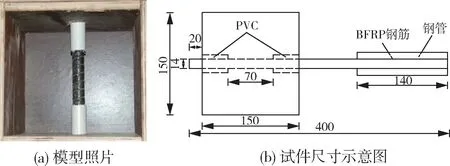
图1 试件的模型照片和尺寸示意图Fig.1 Model photos and dimensional diagrams of the specimen

试验采用一种充满环氧树脂的钢管锚固系统对BFRP筋施加拉拔力，以确保在试验过程中夹具与BFRP筋不发生相对滑移。各混凝土试件编号及黏结性能汇总于表1。

1.4 性能测试与结构表征

试验方案布置如图2所示。试验在伺服液压试验机上进行，加载速率为0.014 mm/s。为确保应力均匀分布，在混凝土试件表面安装5 mm厚钢板，通过4根螺纹钢筋和8个四角螺母进行紧固。整个加载过程中，不允许试件出现垂直于加载方向的位移。采用荷载传感器实时测量拉拔荷载值。在BFRP钢筋自由端和钢板表面分别安装1支线性可变差动位移传感器（LVDT）。采用2 Hz的DH5922数据记录仪，实时采集荷载传感器和LVDT的试验数据。试验设置了每个循环加载端滑移位移为3.50 mm，小于单调加载下对应的滑移量3.90 mm［6］。

图2 试验装置布置图Fig.2 Layout of the test equipment

2 结果与讨论

2.1 破坏模式分析

玄武岩纤维增强聚合物筋（直径为12 mm和14 mm）与混凝土界面破坏形态如图3所示。可以看出，BFRP筋外层出现剪切分层，且BFRP筋周围混凝土出现破坏，因此循环拉拔荷载下破坏模式为组合破坏，即BFRP筋表面剪切变形和界面混凝土的破碎。具体来看，BFRP筋被缓慢地从混凝土块中抽出，而混凝土表面没有出现明显的裂缝。由于BFRP筋的抗剪性能相对较弱，在埋设长度范围内，BFRP筋的表面筋存在局部磨损和剥落。同时，部分脱落纤维已黏附在混凝土黏结界面上，BFRP筋在预埋长度区域内出现部分肋痕磨损。与FC14试样相比，FC12试件BFRP筋表面纤维脱落更为明显，说明小直径BFRP筋具有更高的拉拔荷载和更强的界面锚固力。此外，可以发现黏结段界面处部分混凝土发生磨损，少量破碎混凝土随BFRP筋一起被拉出，大大削弱了BFRP -混凝土界面处的摩擦和黏附力作用。

图3 BFRP筋混凝土试件的破坏照片Fig.3 Photos of the destroyed BFRP concrete specimen

2.2 黏结滑移量

试验测得各试件在循环荷载作用下的黏结应力-滑移关系，得出黏结强度及对应的滑移量，结果分别见表2和表3。

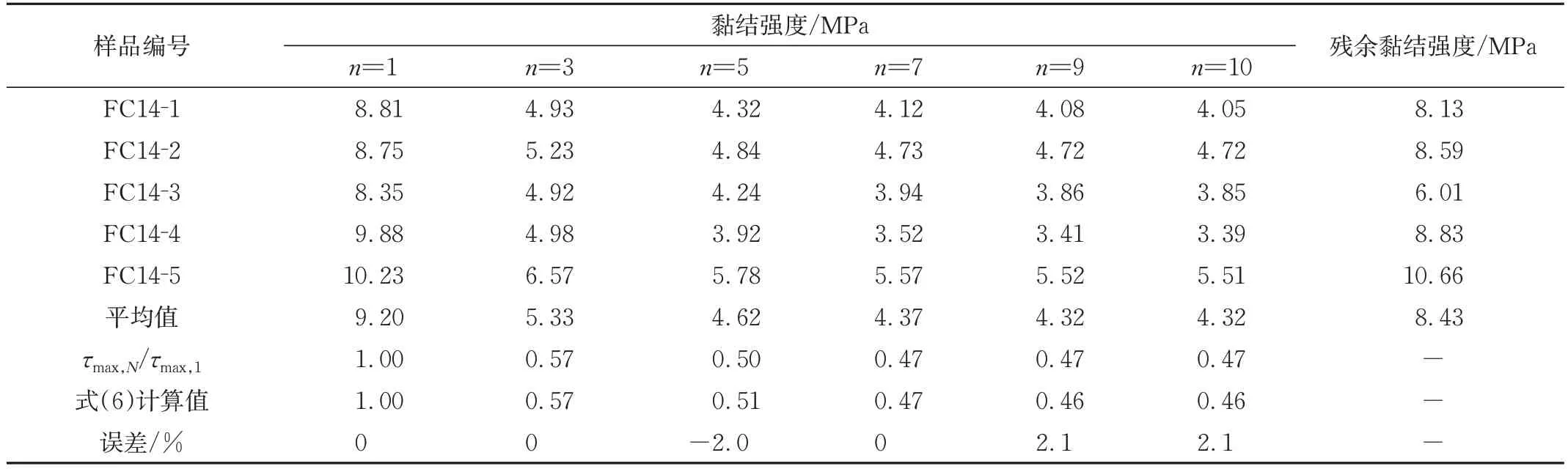
表2 循环荷载下黏结强度的试验和计算拟合结果Tab.2 Test and calculation fitting results of bond strength under cyclic load

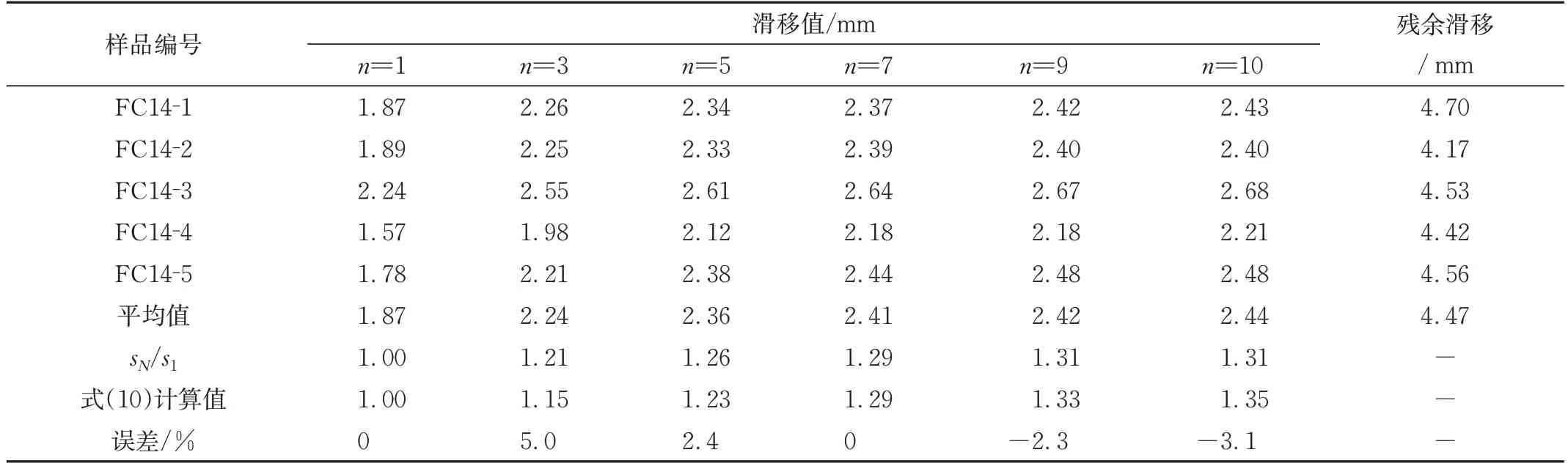
表3 循环荷载下滑移值试验和计算拟合结果Tab.3 Test and calculation fitting results of slip value under cyclic load

实际上，钢筋与混凝土之间的黏结应力沿埋置长度的分布为非线性的。对于拉拔试验，采用3～5倍钢筋直径的黏结长度，可以最大限度减少黏结区非线性应力分布的影响［14］。在本研究中，黏结长度为BFRP筋直径的5倍，因此黏结应力在黏结长度范围内可视为均匀分布，黏结强度计算公式［15］如式（1）所示。

式中 τmax——黏结强度，MPa

F——峰值拉拔荷载，kN

D——BFRP筋的直径，mm

la——黏结长度，mm

BFRP筋的黏结滑移可由式（2）求得：

式中 sfree——BFRP筋黏结滑移，mm

sbar——BFRP筋自由端的位移，mm

scon——固定在混凝土贴合钢板上的位移，mm

2.3 循环荷载作用下黏结应力-滑移曲线

循环荷载下，BFRP筋与混凝土黏结应力-滑移关系试验曲线如图4所示。基于图4，可抽象出某一循环荷载下黏结应力-滑移曲线的一般示意图（图5）。黏结应力-滑移响可分为4个阶段。考虑到加载和反向加载响应的对称性，这里仅对前半周期进行描述：

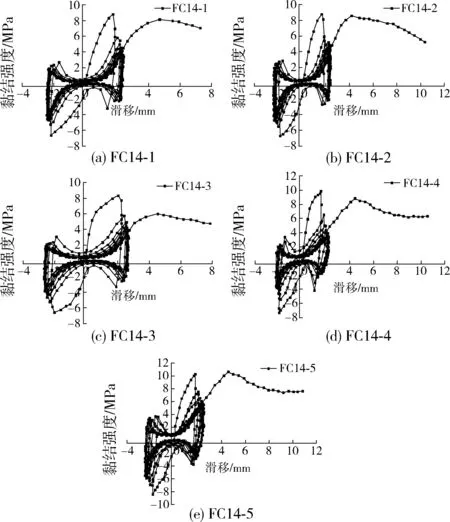
图4 不同试件黏结强度与滑移关系曲线Fig.4 Relationship curve between bond strength and slip for different specimens

图5 循环加载下的黏结应力-滑移曲线示意图Fig.5 Schematic diagram between bond stress and slip curve under cyclic loading

第一阶段为弹性阶段（OA段）：黏结应力小于黏结强度的40 %（A点），呈线性变化。受力初期，黏结阻力主要由BFRP筋与混凝土机械咬合提供。由于机械咬合作用很弱，造成的破坏很小，因此该阶段的滑移主要是由BFRP筋弹性变形引起的。

第二阶段为裂纹扩展阶段（AD段）：随着拉拔荷载的增加，BFRP筋端部混凝土出现局部破碎和裂缝扩展，黏结滑移响应呈现非线性。AD段又可细分为3个子阶段：初始裂纹扩展（AB段）、稳定裂纹扩展（BC段）、不稳定裂纹扩展（CD段）。对AB段，黏结应力小于黏结强度的80 %，劣化仍不明显；随着荷载的增大，筋端部混凝土开始出现细小裂纹，卸荷后完全闭合；到BC段，原始细裂纹继续扩展，萌生多个新细裂纹，黏结劣化更明显；对CD段，黏结应力迅速下降，滑移小幅增加。由于大量细裂纹出现不稳定扩展，BFRP筋受到周围混凝土的约束力迅速弱化。微裂缝开始串联为宏观裂缝，破碎程度加重。

第三阶段为裂缝闭合阶段（DE段）：BFRP筋仍与周围混凝土充分接触，在反方向拉拔荷载下，促使先前萌生的裂缝完全闭合，黏结应力迅速下降。另外注意到，当应力降至0（E点）时，滑移值并不为0，这是由于混凝土局部损伤和BFRP筋非弹性变形引起的残余滑移，且二者均不可逆。

第四阶段为摩擦阶段（EG段）：达到E点后，拉拔载荷变为反向施加，出现的摩擦力分为静摩擦和动摩擦。对于静摩擦（EF段），黏结应力增加迅速，滑移小，F点的黏结应力最大值约为D点的30 %；对于动摩擦（FG段），该部分的黏结应力很小，界面粗糙度和径向压缩是影响此阶段变形的主要因素。当滑移减小到0（G点）时，BFRP筋周围混凝土被压碎而损坏。

2.4 BFRP聚合筋直径对黏结强度的影响

图6给出了直径12 mm和14 mm的BFRP聚合筋混凝土在第N个循环下黏结强度τmax，N与第1个循环下黏结强度τmax，1之比与循环次数N之间的关系。对于所有试件，N=1时对应的黏结强度最大。随着N的增加，黏结强度先迅速减低（1≤N≤4），然后再逐渐趋于平缓（N＞4）。

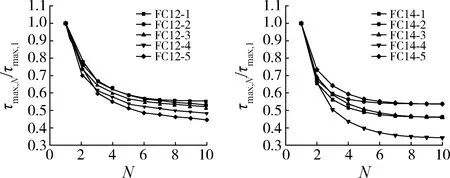
图6 黏结强度比与循环次数的关系曲线Fig.6 Relationship curves between bond strength ratio and number of cycles

另外，同一N下，随BFRP筋直径增大，τmax，N/τmax，1之比降低，这表明增大直径会降低BFRP筋与混凝土的黏结强度。原因是BFRP筋与混凝土的黏结面积与BFRP筋截面周长成正比，而拉力与BFRP筋截面面积成正比，二者的比值反映BFRP筋的相对黏结面积。直径较大的BFRP筋相对黏结面积较小，对黏结性能不利，导致BFRP筋与混凝土的黏结强度降低。

钢筋与周围混凝土的黏结劣化取决于混凝土的损伤程度，而混凝土的损伤程度与循环加载过程中的能量耗散E密切相关。在文献［16］循环剪切下平面模型中引入了损伤函数d，如式（3）所示：

式中 d——损伤函数

E——累积剪切能量耗散

E0——在单调荷载下平面剪切应力-应变曲线下面积常数

为进一步分析，将文献［16］与文献［17］试验结果进行对比，并提出更符合BFRP筋黏结强度的计算式。基于钢筋混凝土的拉拔试验，提出黏结强度与循环荷载次数的关系，对不同混凝土类型或钢筋类型均适用，如式（4）～（5）［17］所示：

式中 un——第n个循环黏结强度，MPa

u0——第一次循环黏结强度，MPa

n——循环次数

s——滑移量，mm

speak——单调加载下黏结强度对应的滑移量，mm

另外，基于混凝土中植入钢筋的拔出试验，文献［18］提出了黏结强度的劣化模型，如式（6）～（7）所示：

式中 uN——第N次循环的黏结强度，MPa

u0——第1次循环的黏结强度，MPa

N——循环次数

s——滑移量，mm

ssp——劈拉强度对应的滑移量，mm

将本文试验结果与式（5）计算得到的黏结强度比

τmax，N/τmax，1进行对比分析，如图7所示。可以看出，黏结强度试验数据处于文献［17］、［18］提出的模型预测范围以内，这表明玄武岩纤维增强聚合物筋混凝土的黏结性能低于钢筋混凝土，而高于植入式钢筋混凝土，且本文试验数据是合理可靠的。

为了更准确预测BFRP筋的黏结强度，对τmax，N/τmax，1与N的数据散点图进行多项式拟合，提出式（8）。

其中A、B、C和D为待定系数。通过回归分析确定待定系数：A=0.74、B=0.75、C=1.82、D=-0.33，R2=0.99。由式（8）计算结果见表2，当N=1～10时，τmax，N/τmax，1=1.00～0.46，与实测数据的偏差处于2.0 %～2.1 %之间，误差很小。因此，可采用式（8）来计算循环荷载下BFRP筋与混凝土的黏结强度。

2.5 循环次数对黏结滑移的影响

图8给出了第N次循环黏结强度对应的滑移sN与第1次循环黏结强度对应的滑移s1之比与循环次数N的关系曲线。随着N的增加，滑移量先迅速增加，再逐渐趋于缓慢。这是由于BFRP筋与混凝土接触界面存在许多原生微孔洞，在循环荷载作用初期，容易发生滑移，滑移速度较快；而随着N的不断增加，界面区大部分微孔洞和裂隙在黏结应力下逐渐被挤压，甚至闭合，混凝土密实度增大，界面滑移速度逐渐趋缓。

根据钢筋循环拉拔试验，文献［19］中提出了钢筋黏结强度对应的滑移模型，如式（9）所示：

式中 sN——第N次循环黏结强度对应的滑移量，mm

s1——第1次循环黏结强度对应的滑移量，mm

基于循环荷载下带肋钢筋拉拔试验，文献［20］提出了与黏结强度相应的滑移模型，如式（10）所示：

基于恒应力循环荷载试验，文献［21］中提出了与黏结强度相对应的滑移模型，如式（11）所示：

将试验数据与式（9）计算得到的sN/s1结果对比见图9。发现式（9）计算预测值略微偏低。因此，延用文献［21］提出的模型，将γ重置为待定参数，如式（12）所示：

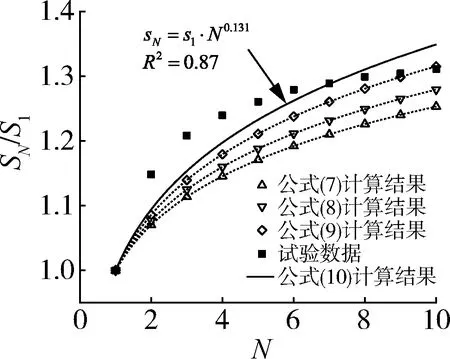
图9 滑移比的计算结果与试验数据对比Fig.9 Comparison between the calculation results of slip ratio and experimental data

对于试验数据进行回归分析，确定系数γ=0.131，此时R2=0.87。由式（10）计算结果见表3。当N=1～10时，sN/s1=1.00～1.35，与试验结果的偏差值处于-2.3 %～4.3 %，偏差很小。因此，可采用式（10）预测循环荷载下BFRP筋的滑移量。

2.6 循环次数对滞回面积的影响

某一循环周期下，黏结应力-滑移曲线所围成的滞回面积大小表征该循环下的能量耗散［22］，而耗能能力是评价混凝土抗震和疲劳性能的重要指标［23］。图10给出了第N个循环滞回面积AN与第1个循环滞回面积A1之比与循环次数N的关系。从图10可见，所有试件的滞回面积在N=1时最大，随N的增加，AN先迅速减小，而后减小速度逐渐趋缓，这与式（8）描述的黏结强度变化规律相似。因此套用式（8）形式，AN/A1随N的关系如式（13）所示：

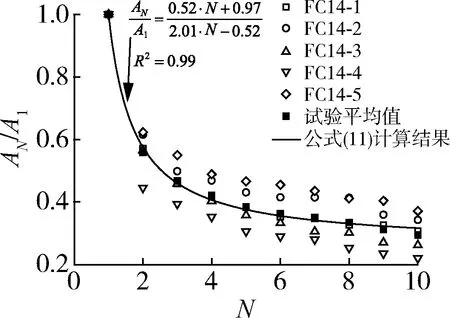
图10 滞回曲线面积比的计算结果与试验数据对比Fig.10 Comparison between the calculated results of hysteresis curve area ratio and experimental data

通过回归分析（图11）可确定待定系数：a = 0.52、b = 0.97、c = 2.01、d = -0.52，且R2=0.99。通过式（13）计算结果见表4。从表知，当N=1～10时，AN/A1=1.00～0.31，与试验数据的偏差值处于-6.9 %～2.9 %，偏差很小。因此，该式可用于预测循环荷载下BFRP筋加固混凝土结构的抗震和疲劳行为。

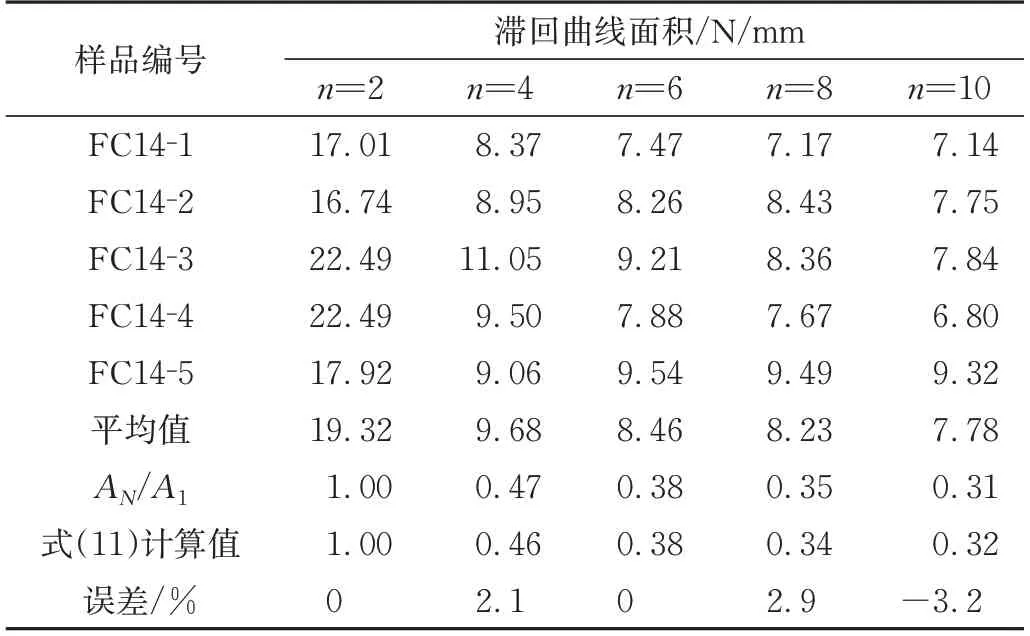
表4 循环荷载下滞回曲线面积试验和计算拟合结果Tab.4 Test and calculation fitting results of hysteresis curve area under cyclic load

3 结论

（1）在循环拉拔荷载下黏结行为经历了弹性阶段、裂缝扩展阶段、裂缝闭合阶段和摩擦阶段；

（2）随BFRP聚合物筋直径的增大，BFRP 聚合物筋-混凝土界面τmax，N/τmax，1之比降低，即增大直径降低了BFRP 筋-混凝土的黏结强度；

（3）循环拉拔荷载下，BFRP筋与混凝土的黏结强度随循环次数的增加而减小，并提出了考虑循环次数的BFRP筋与混凝土黏结强度模型；BFRP筋与混凝土自由端黏结强度对应的滑移随循环次数的增加而增大，并提出了考虑循环次数的BFRP筋与混凝土黏结滑移预测模型；BFRP筋与混凝土之间的滞回曲线面积随着循环次数的增加而减小并提出了BFRP筋与混凝土黏结滞回面积的预测模型。