数控机床XY工作台插补中滤波技术

陈振炜,李艳林,阴雷鸣,朱进全

(济南邦德激光股份有限公司,济南 250000)

0 引言

插补运算过程中,为提升加工效率,利用速度前瞻技术[1-2]使得程序段与程序段之间衔接速度不为零;而一般速度规划与插补计算的都是程序段的切向速度,故在衔接过程中,因为加工轨迹的转向或者程序段之间的曲率不连续,会产生突变的转向加速度[3-4],从而使得加工过程中产生机床振动。目前国内外对于插补中结合滤波的算法研究成果丰富,于东等[5]提出一种结合滤波技术以及直线加减速规划的方法,在传统的直线加减速后面串联一个滑动滤波器,通过滑动滤波器来解决加速度跳变问题,但解决的问题是单独程序段通过直线加减速时,直线加减速算法本身在单个程序段进行加减速时存在的加速度突变问题。杨东升等[6]提出的基于前瞻-滤波的加减速算法,提高了加工速度,有效解决了运动中震动的问题,但未考虑段与段的衔接位置速度转向带来的加速度突变。高敏等[7]提出的数字卷积加减速算法,通过对固定速度进行两次卷积,实现高柔性S形加速度曲线。李冬冬等[8]利用FIR滤波器,对速度和加速度滤波进行三次滤波,生成平滑的高阶参考轨迹,通过调节进给脉冲的重叠时间,精确控制拐角轮廓误差。LUIGI等[9]提出一种FIR滤波器生成高阶轨迹的基本方法。CHEN等[10]提处一种FIR滤波方法能减小刀具震动。以上方法皆未讨论如何使用滤波器处理衔接段之间加速度突变的问题处理。

为解决程序段之间的衔接处的加速度突变问题。本文在数控机床XY工作台下,使用S形加减速插补方法,在此基础上提出一种适用于插补的滤波处理方法,该方法能有效解决程序段衔接处加速度突变问题。通过对整个运动段进行速度滤波是提升加工运动平稳特性的方法之一,将数控系统各个单轴速度量低通滤波,消除其高频成分,使得各个单轴速度曲线变得平滑,加速度变得连续,从而抑制机床震动。本文提供一种各个轴位置点实现速度滤波的方法,通过将各个单轴的插补位置直接输入低通滤波器滤波器分别进行滤波,滤波输出的各个单轴的点作为最终输出轴的位置点,以此达到速度滤波效果。在插补之后进行滤波,会使得运动段在衔接处以及圆弧段上产生一定轮廓误差,本文还分析了滤波产生的轮廓误差进行控制的方法;并且对滤波后产生的进给量过小问题进行分析并做补偿处理。

1 基于数字滤波器的插补滤波方案

1.1 FIR滤波器设计分析

主要分析对单轴进行滤波时FIR滤波器满足的条件。首先分析滤波器的原理,记滤波器系数为h(n),假设离散输入信号为x(n),输出信号为y(n),则有滤波器输出值为:

y(n)=x(n)*h(n)

(1)

式中:*表示卷积运算。

典型的FIR滤波器单位样值响应如图1所示,对于FIR数字滤波器,单位样值响应的系数值就是FIR滤波器的系数值。在加工图形时,对各个轴速度进行滤波,假定在一个周期内只有单位速度信号为1 mm/s,系统插补周期为1 ms,则在该周期加工时,加工所经过的直线距离为0.001 mm,当经过FIR滤波器滤波后,其输出的速度波形形状同样如图1所示,即将单位速度信号展开。若滤波器响应有负值,则表明速度出现负值,在一维加工过程中会产生反向加工,二维加工过程中可能会产生不必要的振荡波纹或螺旋线,这是加工过程不允许的。

图1 典型的FIR低通滤波器单位样值响应

综上所述,本文规定滤波器系数全为正值。同时,加工长度要前后一致,故滤波器系数和必须为1,即需要将滤波器为归一化。同时规定使用的FIR滤波器为线性相位滤波器,也即是其滤波器系数对称。

1.2 各单轴位置点滤波卷积运算实现速度滤波原理

假设滤波器长度为M,则在滤波过程中,当第i个速度值进行滤波时,可以计算滤波后的位置点,有如下关系:

当i≤M时,有:

(2)

式中:Ts为插补周期,(P0,P1,…,PM,…)为插补序列,Pi为当前插补周期插补点,Pi-1为前一个周期的插补点,(α0,α1,…,αM)为滤波器系数,(Q0,Q1,…,QM,…)为滤波器输出点。将上式展开并处理,即有:

Qi=P0+α0(Pi-P0)+α1(Pi-1-P0)+…+

αi-1(P1-P0)+αi(P0-P0)+…+αM(P0-P0)=

α0Pi+α1Pi-1+…+αi-1P1+αiP0+…+αMP0

(3)

同理,当i≥M+1时,有:

Qi=P0+α0(Pi-P0)+α1(Pi-1-P0)+…+

αM-1(Pi-M+1-P0)+αM(Pi-M-P0)=

α0Pi+α1Pi-1+…+αM-1Pi-M+1+αMPi-M

(4)

综合上述分析得出一个重要结论,在进行插补后,对各个单轴速度进行滤波,可以通过直接对各个轴位置点进行滤波卷积运算实现。利用滤波器输入数据与滤波器系数卷积,得到滤波器输出点,在滤波起始位置,以及滤波终止位置需要对滤波进行如下操作:假设用一个队列存储需要与滤波器卷积的数据,称为滤波数据点队列,该队列长度与滤波器长度一致。初始化时将滤波数据点队列全部初始化为运动段起始点,然后将粗插补点逐个压入滤波输入数据点队列运算,在插补结束时,将最后一个插补点重复压入滤波数据点队列运算,直到队列全部变为最后一个插补点即滤波结束。

1.3 滤波产生的轮廓误差及误差控制的方法

分析滤波器阶数、滤波器中心频率以及拐角处的速度对轮廓轨迹误差的影响,加工最大速度为500 mm/s,加工加速度为10 000 mm/s2,最大加减速时间为50 ms,插补周期为1 ms。图中选用汉宁窗,设定拐角衔接处速度为200 mm/s,如图2a所示,分析程序段之间衔接的夹角为直角时轮廓误差随着滤波器阶数以及中心频率的变化,图2a中可以发现,随着滤波器截止频率的增加,拐角误差并未产生任何变化,表明滤波器的截止频率对拐角误差无影响。同时随着滤波器阶数的增加,拐角误差逐渐增大,同时若要求加工过程中不会产生过冲现象,则滤波器的系数则必须大于零,此时经过计算得到滤波器阶数与滤波器的截止频率限制区间如图2a渐变区域所示,该区域为参数可选区间,空白部分表示在该区间的参数会使得滤波器阶跃响应产生过冲,从而影响加工。该结论可以扩展到任意类型的程序段衔接的误差规律中,即对于任意的程序段衔接,经过FIR低通滤波器滤波后,滤波器的中心频率对拐角误差无影响,滤波器的阶数与拐角误差正相关,并且滤波器可选参数区间类似于图2a中所示的渐变区域。图2b为选定FIR滤波器为汉宁窗,滤波器中心频率为20 Hz时,拐角大小为π/50时,拐角速度以及滤波器阶数对拐角误差的影响,分析可知,随着拐角速度的增加,拐角误差逐渐增加。

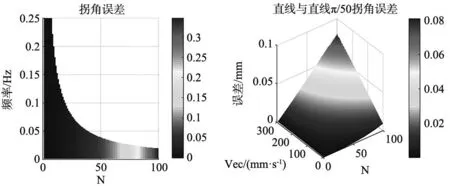
(a) 拐角误差随着滤波阶数、滤波截止频率的变化 (b) 拐角误差随着滤波阶数、拐角速度的变化

分析圆弧曲线误差随着滤波器阶数以及拐角速度的变化,选定FIR滤波器为汉宁窗,滤波器中心频率为20 Hz,圆弧半径为50 mm,图3a为直线与圆弧相切时的曲线误差,因为直线相切,误差主要由加工圆弧时曲线误差引起,此时随着滤波阶数的增加曲线误差逐渐增加,滤波阶数一定时衔接处的速度对曲线误差的影响较小。图3b为圆弧与圆弧夹角为π/2时,总的轮廓误差随着拐角速度的变化,分析可知,随着拐角速度的增加,轨迹误差呈现折线形式,表明在拐角速度较小时,曲线误差为轮廓误差的主要因素。随着拐角速度的增加,拐角误差的影响超过曲线误差,此时由拐角误差为轮廓误差主要因素。

(a) 直线与圆弧衔接轮廓误差 (b) 圆弧与圆弧衔接轮廓误差

定量分析如何通过参数的约束限制曲线误差以及拐角误差。在插补后对各轴进行速度滤波,使得圆弧以及拐角处产生轮廓误差;为将误差限制在预设范围内,本文使用的方法是,在速度规划时,提前通过轨迹误差计算拐角衔接处的速度限制以及圆弧的最大速度限制,再进行速度规划,从而达到控制滤波带来的拐角误差与曲线误差的目的,下面来分别分析滤波器产生的拐角误差与曲线误差的与速度规划的关系。本方法基于S形加减速算法进行计算,其他类型的加减速算法可以类比得到。

首先分析滤波对圆弧曲线误差的影响,滤波器的奇偶性对误差影响较小,在此只对偶数阶滤波器进行分析,对于假设某一段圆弧的在做插补后起点到终点的插补点的位置为:

P=(P0,P1,…,PN,…,P2N)

(5)

长度为2N+1 。

假定滤波器系数为α=(α0,α1,…,α2N),则通过滤波之后得到的新的插补点为:

Q=(Q0,Q1,…,Q2N,…,Q4N)

(6)

图4 圆弧曲线误差

δs=|Q2N-PN|

(7)

式中:δs为曲线误差,滤波后得到的点为:

(8)

根据式(8),此时:

(9)

式中:

Pi+P2N-i-2PN=2R(1-cosθi)e

(10)

式中:i∈(0,1,…,N-1),R为圆弧曲率半径,e为PN指向圆心的单位向量,θi为Pi与PN所夹圆心角。

定义:

(11)

式中:v为圆弧最大速度,Ts为插补周期。

将式(10)和式(11)代入式(9),可以得到误差为:

(12)

于是,在速度规划时,圆弧最大速度有:

(13)

综上所述,通过S形加减速进行插补时,若给定曲线误差δs,圆弧半径R,插补周期Ts,滤波器系数α,滤波器阶数2N, 即可以在速度规划阶段通过式(13)限制圆弧最大速度,从而使得滤波后误差不会超过限制。

再分析滤波对拐角误差的影响,在此给出特定条件下的误差分析表达式,本文分析拐角误差时,使用的程序段轨迹皆为直线段,并且使用S形加减速,当衔接的程序段为其他类型时,可以近似的用本文分析的拐角误差替代。与圆弧曲线误差分析一致,如图5所示,此时定义误差:

δc=|Q2N-PN|

(14)

则有:

(15)

在满足S形加减速条件下,此时规定在拐角处产生误差拐角误差时处于S形加减速的第一阶段,即此时有:

(16)

式中:TA为最大加减速时间,Ts为插补周期。

此时有误差:

δc=|Q2N-PN|=

(17)

式中:当拐角速度为零时,可知:

(18)

式中:amax为最大加速度,β为直线的夹角,d为直线角平分线PN指向Q2N的单位向量。

当拐角处速度为零时,根据式(17)和式(18)可得:

(19)

然后分析,当拐角速度不为零时,拐角误差的表达式,则此时拐角速度不为零,式(18)变为:

(20)

式中:J为加加速度。

于是有一般拐角误差为:

(21)

此时,在速度规划中通过误差对拐角处规划速度进行限制,即有:

(22)

综上所述,通过S形加减速进行插补时,若给定拐角误差δc,插补周期Ts,拐角处夹角β,滤波器系数α,滤波器阶数2N,即可以在速度规划阶段通过式(22)限制拐角处速度,从而使得滤波后拐角误差不会超过限制。其中要求其滤波器阶数满足式(16)。同时分析可知,拐角处通过滤波后,会产生最小拐角误差,即给定的拐角误差必须必最小拐角误差大。

1.4 滤波的延时补偿问题

在滤波过程中,因为在程序段的起始以及末尾处的速度较小,此时经过滤波之后会产生大量的速度较小的值,当该段速度小于伺服驱动最小脉冲长度时,电机不会产生运动,造成刀具在该处停留时间过长产生大量延时,一方面降低的加工效率,另外一方面,在某一点切削时间过长对于零件成形的质量造成影响。为提升系统性能,必须对程序段进行滤波的起始位置以及尾部位置进行处理。

先分析插补序列,假设有插补序列为(P0,P1,…,PN,…),滤波器系数为(α0,α1,…,αN),滤波后得到的点为(Q0,Q1,…,QN,…),于是输出第一个点的位置为:

Q0=P0

(23)

速度滤波后,输出的第二个点位置:

Q1=P0+α0(P1-P0)

(24)

分析极端情况,即当初始速度为零,初始加速度为零时,使用S形加减速,此时,假设处在加加速阶段,分析第一个点:

(25)

式中:amax为最大加速度,Ts为插补周期,TA为最大加减速时间,于是:

(26)

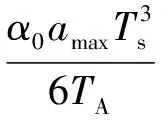
(27)

分析可知,在加工开始阶段,此时有几个脉冲周期刀具不动直到插补速度足够大,电机才能开始运动。此时需要丢弃一个周期内进给长度小于伺服一个脉冲长度的插补位置点,即称为通过滤波器进行延时补偿。

滤波补偿分为在滤波开始时以及滤波即将结束时进行,如图6所示, 假设用一个队列存储需要与滤波器卷积的数据,称为滤波数据点队列,该队列长度与滤波器长度一致。在滤波起始阶段,当插补点压入队列时并不进行滤波运算,也不输出滤波点,直到压入队列的插补点为第(N+1)/2个时,才开始将第一次卷积运算,并将滤波点输出,以后每个周期都进行滤波输出。在滤波结束阶段,当插补结束时,将最后一个插补点重复压入滤波数据点队列运算,当压入的最后一个插补点的次数达到(N+1)/2次时,直接结束滤波运算。其中(N+1)/2为N+1的1/2并向下取整的整数。

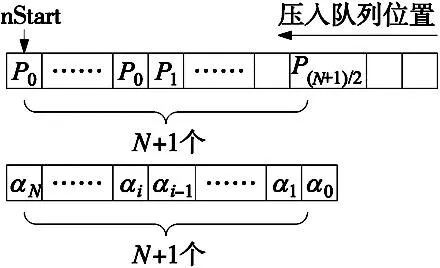
图6 延时补偿原理

为进一步理解补偿作用,给出补偿效果示意图如图7所示,坐标(29.191,92.235)的位置为速度为零的点,在此处开始加减速。此时如果不存在滤波补偿,插补点在坐标(29.191,92.235)处聚集,此时影响加工质量与加工效果,当加上滤波补偿之后,此时可知插补点变少并且分散,从而提升了加工效率并且提升加工质量。

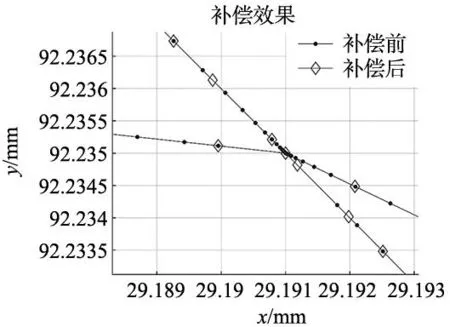
图7 滤波补偿前后轨迹对比放大图

1.5 基于滤波的插补算法的设计与实现

分析可知,在滤波过程中,其滤波的算法流程如图8所示。其具体算法步骤为:

图8 滤波插补算法流程图

步骤1:初始化程序段参数;

步骤2:在速度规划时,通过滤波的曲线误差限制圆弧的最大速度,通过滤波的拐角误差限制程序段之间的衔接速度,并进行速度规划;

步骤3:通过S形加减速进行插补;

步骤4:将插补的位置点输入滤波器进行滤波。

2 仿真结果及分析

为了进一步说明本文方法,下面给出一组参数进行分析,假设加工G代码为:

G0 X0 Y0 F150000
G1 X5 Y0 F120000
G1 X5 Y3
G1 X0 Y3
G1 X0 Y0

其他部分参数设置如下:插补周期:0.001 s,最大加速度:10 000 mm/s2,最大速度:200 mm/s。如图9可知,滤波后轨迹闭合,与滤波前轨迹在起点位置,终点位置以及直线处重合,在拐角处有一定的误差。该误差可通过滤波限速控制。表明通过对插补点直接进行滤波,起始位置以及终止位置不会产生偏差,在直线处,轨迹不会产生偏差。

图9 滤波前后轨迹对比图

如图10所示,观察对比滤波前后X轴速度以及Y轴速度,可知不平滑处的速度通过滤波后速度变得平滑,而总的加工时间略有增加。

(a) X轴速度 (b) Y轴速度

如图11所示,在滤波前加速度有几个突变的点,即对应于轨迹的拐角处,此时该突变点会给机床造成瞬时冲击,使机床产生震动,通过滤波之后,运动段之间的加速度突变被消除,机床柔性冲击得以消减。经过低通滤波后,在对直线加工时,会平滑加工的速度曲线,使得机床运动更加柔和,并且能展开突变的加速度分量,减缓机床运动对机床的冲击,减小了机床震动发生的可能,但会产生拐角误差。在对圆弧进行加工时,平滑效果不大,会产生曲线误差。

(a) X轴加速度 (b) Y轴加速度

如图12所示,观察滤波前后的路程-速度关系图可知,在该G代码参数情况下,经过滤波后,在速度最小处,即是拐角处,速度得到一定提升。同时滤波前的距离-速度图横坐标能达到16 mm,而滤波后横坐标,即距离小于16 mm,表明滤波后总加工长度变小,其原因在于拐角处的内缩,导致滤波后的加工长度略小于滤波前的总长度,但通过限速拐角误差可以控制在限定范围内。

图12 滤波前后路程-速度关系图

下面再给出另一组参数讨论误差控制效果,其加工假设加工G代码为:

G00 X0 Y0
G01 X5 Y10
G01 X10 Y0

其他部分参数设置如下:插补周期:0.001 s,最大加速度:10 000 mm/s2,最大速度:200 mm/s,拐角精度:0.01 mm。滤波器使用FIR布莱克曼窗函数滤波器,阶数为15阶。

如图13所示,在误差限制条件为0.01 mm时,未采用误差控制时,实际加工轨迹与未加滤波时的轨迹拐角处误差约为0.02 mm,超过了给定的误差限制,使用误差控制后,最终插补滤波后得到拐角的限制精度为0.01 mm,达到给定拐角精度要求。

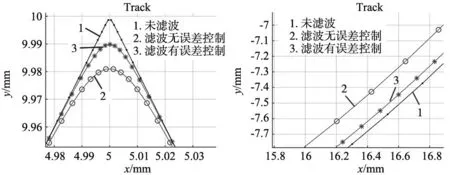
图13 未滤波轨迹、滤波未采用误差控制轨迹以及滤波采用误差控制轨迹拐角对比

再给出一组圆弧的G代码,对比圆弧误差控制效果,如下:

G00 X0 Y0
G02 X20 Y0 I10 J0
G02 X0 Y0 I-10 J0

其他部分参数设置如下:插补周期:0.001 s,最大加速度:10 000 mm/s2,最大速度:200 mm/s,曲线精度:0.05 mm。滤波器使用FIR布莱克曼窗函数滤波器,阶数为15阶。

如图14所示。在误差限制条件为0.05 mm时,在做误差控制时,实际加工轨迹与未加滤波时的轨迹拐角处误差约为0.25 mm,超过了给定的误差限制,使用误差控制后,最终插补滤波后得到拐角的限制精度为0.05 mm,达到给定拐角精度要求。

3 结论

首先,根据直接将各个轴的插补点位置作为滤波器输入,计算结果是位置点,作为滤波输出,即达到对各个轴的速度进行滤波的效果,简化了速度滤波计算流程。通过滤波后,使得机床运动平缓,消除了机床柔性冲击,抑制机床震动,提高机床加工稳定性以及加工精度;其次,采用本文中针对速度滤波给定误差限制速度的方法有效解决了滤波后产生的误差精度不可控的问题;最后,通过滤波脉冲补偿之后,此时在准停点密集的点位被减少,提升了系统加工效率,提升系统性能。

通过在插补过程中加入对轴的滤波流程,在满足给定误差的要求下,提升的机床运动的平滑性,提高了加工质量。下一步将针对五轴的轴关节滤波及相应的误差控制开展研究。