精密导向膜片设计与优化*

周洪海,秦 超,徐振邦,王学问,巩 浩,陈 洋

(1.中国科学院长春光学精密机械与物理研究所,长春 130033;2.中国科学院大学,北京 100049;3.中国科学院空间光学系统在轨制造与集成系统重点实验室,长春 130033)

0 引言

随着精密光学技术的不断发展,光学设施对精密调整机构的精度要求越来越高,有的甚至达到纳米、亚纳米级水平[1-3]。传统的导向或调节机构如导轨、丝杠螺母、凸轮机构等,存在摩擦、侧隙、需要润滑、精度低等缺点。而且在制造和组装过程中也存在不可避免的误差。虽然有着大行程、高稳定性等优点,但并不适用于超精密导向、调整领域。

为了解决这些问题,柔性机构逐渐成为当下的研究热点。相对于传统的导向或调节机构,柔性机构具有更小的体积、更高的灵敏度、没有机械摩擦和齿隙等优点,被广泛应用于高性能显微镜、光刻机物镜系统、微定位台等精密调整、导向机构中[4-9]。通过使用柔性机构代替传统机构,可以实现纳米甚至亚纳米级的高精度调整,从而满足现代光学技术所需的要求[10]。因此,柔性机构将成为未来精密光学技术中不可或缺的一部分。

曾超等[11]设计了一种纳米精度的位移机构,采用平面连杆柔性铰链实现了0.2 mm的运动行程和1.1 nm(均方根误差)的高位置稳定性。赵磊等[12]用直梁型柔性铰链代替传统的转动副,设计了一款用于光刻投影物镜中的x-y面内的微动调整机构。张德福等[13]采用由倒角形柔性铰链构成的对称平行四边形机构来实现z向的位置调整。但以上结构的适配性相对较差,整体的位移调整模型需要围绕着柔性铰链搭建。

如图1所示,本文设计了一种以绕中心均匀分布的6条柔性梁为柔性部分的导向膜片。通过6条柔性梁的弯曲来约束中心平台的运动,使光学元件严格沿轴向平移。这种结构表现为低轴向刚度和高径向刚度,能够抑制垂直于运动轴向的寄生运动。而且膜片结构尺寸小、可单独加工。在使用时将膜片固定在基座即可,安装方便,与整体结构的适配性好。

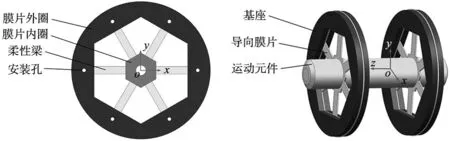
(a) 导向膜片组成 (b) 导向膜片的工作原理

本文采用柔度矩阵法对膜片内圈进行建模,列出柔度矩阵并通过有限元分析验证了公式的正确性。然后根据使用需求,对结构进行了优化,提高了轴向柔度、轴向/径向柔度比和最小应力的指标数值。优化后的结构可用在由小型音圈电机驱动、具有微米级行程的精密导向机构上。

1 精密导向膜片的组成及工作原理

精密导向膜片如图1所示。膜片的柔性由6条绕中心对称的柔性梁组成,膜片的外圈和内圈被固定约束,因为约束后的刚度远大于柔性梁结构,可将膜片内圈,外圈视为刚体。为了增强膜片在受到轴向力时的柔性,可以采取以下措施:减小柔性梁厚度并增大长度,这有助于柔性梁发生弯曲变形。此外,由于轴向运动会产生寄生的径向运动,为了抑制这种运动,需要增大柔性梁宽度,提高其在平面内的抗拉压和抗剪切能力。

2 基于柔度矩阵法的柔度建模

2.1 建立单条柔性梁的柔度矩阵

在导向膜片的使用过程中,膜片外圈不发生运动,膜片内圈和导向杆件的运动相同。由于导向膜片的变形主要集中于柔性梁,此时需要建立柔性梁的柔度模型来分析其支承和导向的性能。如图2所示,柔性梁连接外圈的一端为固定约束,连接内圈的一端为自由端。

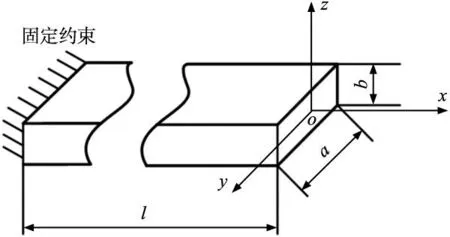
图2 柔性梁末端的局部坐标系

对膜片内圈进行轴向运动和径向运动时的受力分析,轴向运动与径向运动的受力分析图如图3a和图3b所示。

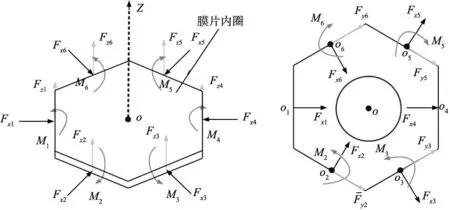
(a) 轴向运动受力分析 (b) 径向运动受力分析

如图3a所示,在膜片发生轴向运动时,因柔性梁的分布为膜片内圈各边的中心,所以6条柔性梁沿各自局部坐标轴x方向力Fx1、Fx2、Fx3、Fx4、Fx5、Fx6它们的作用线穿过膜片内圈的形心,对形心的作用为矢量力的叠加。而沿局部坐标轴z方向的力Fz1、Fz2、Fz3、Fz4、Fz5、Fz6它们会对形心产生力矩作用,对形心的作用为矢量力与力矩的叠加。同理可知在膜片轴向运动和径向运动时柔性梁末端施加给膜片中心Fx、Fy、Fz、My、Mz的作用,根据受力特点列出单条柔性梁末端的局部柔度矩阵。

柔性梁末端受F=[Fx,Fy,Fz,Mx,My,Mz]T的作用,其对应的变形可以表示为:

δ=CF

(1)

式中:变形δ=[Δx,Δy,Δz,Δα,Δβ,Δγ],柔性梁的柔度矩阵Ci(i=1,2,3,…,6)为:

(2)

式中:柔度系数CΔx-Fx、CΔy-Fy、CΔy-Mz、CΔz-Fz、CΔz-My、CΔα-Mx、CΔβ-Fz、CΔβ-My、CΔγ-Fy、CΔγ-Mz分别为:

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

对x轴惯性矩:

Ix=βab3

(13)

对y轴惯性矩:

(14)

对z轴惯性矩:

(15)

2.2 建立膜片的整体柔度矩阵

膜片中6条独立的柔性梁为并联连接。为了获得整个膜片的柔度矩阵,需要将局部坐标系转换为用于描述整个膜片的整体坐标系。

把以各柔性梁末端中心为原点建立的坐标系oi-xiyizi称为局部坐标系,把以膜片内圈中心为原点建立的坐标系o-xyz称为整体坐标系。局部坐标系与整体坐标系的关系如图4所示。以整体坐标系为基准,因6条柔性梁均匀分布,各局部坐标系至整体坐标系的旋转角度θ为0°、60°、120°、180°、240°、360°。局部坐标原点与整体坐标原点的距离为r。

图4 局部坐标系与整体坐标系示意图

如图4所示,设第i条柔性梁在局部坐标系oi-xiyizi的柔度为Ci,根据柔度矩阵法,建立空间变换矩阵Toi将单元柔度矩阵从局部坐标系oi-xiyizi转到整体坐标系上。第i(i=1,2,3,4,5,6)条柔性梁的整体柔度矩阵为:

Coi=ToiCi(Toi)T

(16)

式中:第i(i=1,2,3,4,5,6)条柔性梁的变换矩阵Toi为:

(17)

最后,膜片整体的柔度矩阵为:

(18)

2.3 膜片内圈在轴向力下的运动求解

当施加载荷F=[0,0,1,0,0,0]T时,根据式(18)求出的整体柔度矩阵可以得到变形量为:δ=[0,0,l3/72EIy,0,0,0]T。由上述公式推导结果可知,当膜片内圈受到力Fz,膜片内圈只有z方向的位移。即单条柔性梁末端的x向位移为0,末端转角为0,单条柔性梁以及膜片整体的变形如图5所示。

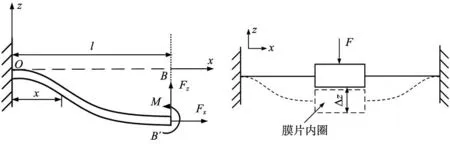
(a) 单条柔性梁的变形示意图 (b) 膜片在x-z平面的变形示意图

从上述分析可知,当受到z向力时,单条柔性梁对膜片内圈有x、z方向的运动以及绕y、z方向的角运动,但关于中心对称的两条柔性梁对膜片内圈x的运动和y、z的角运动相互抵消。只保留了z方向上的位移,z方向上的柔度为:

Cz=l3/72EIy

(19)

2.4 膜片内圈在径向力下的运动求解

在运动元件带动膜片做径向运动时,其对膜片内圈的作用力可认为穿过形心,设其在x-y平面内作用力为Fr、与x轴的夹角为β。用F=[Frcosβ,Frsinβ,0,0,0,0]T表示其对形心的作用力,根据整体柔度矩阵得到变形量δ=[l3/3E(abl2+12Iz)]·[Frcosβ,Frsinβ,0,0,0,0]。由上述公式推导结果可知,膜片内圈在x-y平面内有以下特性:①运动方向与施加力方向相同。②任何运动方向的柔度相同。图6为其效果图。以Cr表示其在x-y平面的柔度。

(a) 单条柔性梁的变形示意图 (b) 膜片内圈在x-y平面的变形示意图

Cr=l3/3E(abl2+12Iz)

(20)

3 结构优化

根据导向膜片的使用特点,优化膜片的3个参数来提升其性能。首先,需要提高导向膜片的轴向柔度以确保其调节和导向能力;其次,需要提高导向膜片的径向柔度,以抑制寄生的径向运动;最后,膜片在运动行程内的最大应力应小于许用应力,且应降低最大应力的值,这能够提高结构的安全可靠性、减少疲劳损伤并降低成本。

3.1 优化目标

3.1.1 轴向柔度

目前,由于音圈电机具有响应速度快、运动部件质量轻、无力纹波、非接触式进给驱动、易于控制等超精密定位特性[14],被广泛应用于精密导向调整机构的驱动装置中。目前直径在5 cm之内的音圈电机驱动力约为0～10 N,为了得到微米级以上的行程,需增大膜片在轴向的柔度,使其至少要大于2×10-3mm/N。

3.1.2 优化轴向/径向柔度比

如图1a所示,在运动元件运动过程中,实际轨迹与理想轨迹的同轴度越小,运动精度越高。本文使用轴向/径向柔度比[15]来衡量运动轨迹的偏离程度。在同样的约束条件和行程下,轴向/径向柔度比越高,轨迹的偏离程度越小,轨迹越接近轴线位置。本文设计的导向膜片轴向/径向柔度比为:

(21)

3.1.3 优化轴向运动最大应力

由第2节分析可知,在膜片轴向运动过程中,单条柔性梁的末端的转角为0,z方向上的位移为w,根据叠加法列出平衡方程:

(22)

(23)

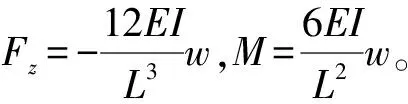
由图7可知,在沿z向运动时柔性梁的最大弯矩可能出现在其两端,分别对两端的弯矩进行计算。

(24)

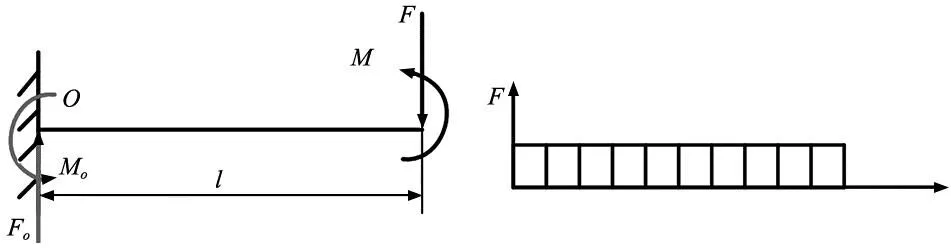
(a) 受力分析图 (b) 剪力图

由推导结果可知,首末两端弯矩的大小相等,方向相反。

(25)

根据公式计算,最大应力出现在柔性梁局部坐标系x=0,y=2/b或x=l,y=2/b处,最大应力值为σmax=3Ebw/l2,w为柔性梁的挠度。

3.2 优化柔性梁的结构参数

根据式(19)、式(21)和式(25)可推导出膜片轴向柔度、轴向/径向柔度比、最大应力值与柔性梁厚度b以及柔性梁长度l的关系,如图8所示。当b变小或l变大时,轴向柔度变大、轴向/径向柔度比变大、最大应力值变小。与期望的优化结果相同。当a变化时,轴向柔度与轴向/径向柔度比变化的方向相反。根据膜片的实际使用要求及柔性梁的特点对a的值进行优化,设置边界条件为:

(26)

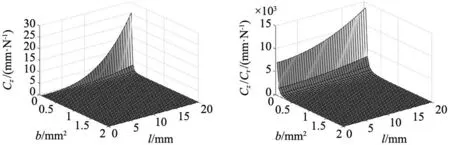
(a) Cz与b、l的关系 (b) Cz/Cr与b、l的关系

式中:[σ]为材料的弹性许用应力,本文膜片使用的铝合金的弹性许用应力约为240 MPa。以a取值范围的中值a=5为标准,赋予轴向柔度、轴向/径向柔度比的权重分别为0.4、0.6建立优化函数:

(27)

U与a的关系如图9所示。U在区间的最大值为1.03,此时a=6。优化前与优化后的参数如表1、表2所示。优化后的膜片的柔度为4.2×10-3mm/N,图8b所示机构在0～10 N驱动力作用下的最大应力值为9.03 MPa,满足使用要求。

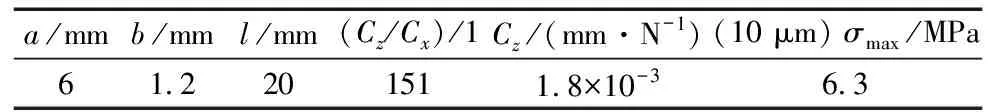
表1 优化前柔性梁参数及理论计算结果

表2 优化后柔性梁参数及理论计算结果

图9 优化函数U随a的变化图

4 柔度模型的有限元和实验验证

图10为有限元分析中的网格图。对膜片内圈在x、y、z方向分别施加1 N的力得到表3和表4的结果,膜片的位移变化云图如图11和图12所示。从表3和表4中可以看出优化前后理论计算柔度与仿真计算柔度x、y方向最大误差为6.7%,z方向的最大误差为4.3%皆处于可接受范围内。仿真结果与计算结果存在误差的原因主要来自两个方面:①网格单元的划分类型与网格质量存在影响;②理论计算中并未将与柔性梁相连膜片内圈的柔度计算在内,而仿真中膜片内圈有微量的变形并与柔性梁结构存在耦合关系,影响了仿真结果。

表3 优化前的有限元计算结果

表4 优化后的有限元计算结果

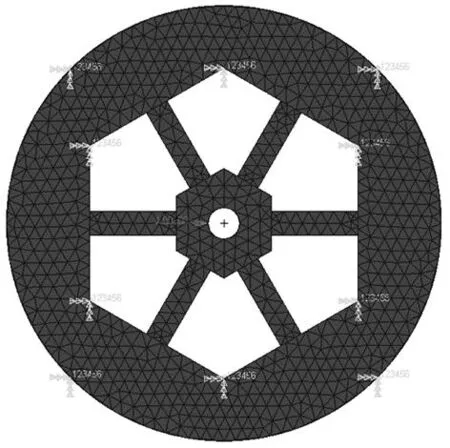
图10 有限元网格图

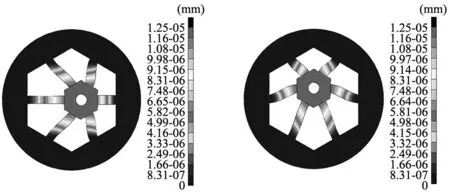
(a) 在x向力作用下 (b) 在y向力作用下

(a) 在x向力作用下 (b) 在y向力作用下

为了验证柔度模型的准确性,搭建了柔度测试系统,其原理如图13所示。压力测试仪用来测量施加在膜片上的z向压力,电子高度尺测量膜片的z向变形量。通过测量不同压力下的z向变形量得到实验结果如图14所示。其中数据拟合曲线的斜率就是膜片的z向柔度。实测模型z向柔度与理论计算柔度的相对误差为7.8%,验证了本文方法的可行性。

图13 柔度测试装置

5 结论

(1)提出了一种具有精密导向作用的柔性膜片,建立其轴向与径向柔度的理论计算模型,并通过有限元分析与实验测试,验证了理论模型的正确性。

(2)分析了单条柔性梁参数对导向膜片轴向与径向柔度的影响。

(3)以导向膜片的高轴向柔度、高轴向/径向柔度比和低应力为目标,建立其优化设计模型,通过对不同目标权重比例的分配,对柔性梁结构参数进行目标优化。优化结果显示,轴向/径向柔度比优化率为172%,轴向柔度优化率为233%,最大应力优化率为32%。优化结果完全符合预期,说明优化结果具有可行性。