多维曲面成形运动规划中三维模型数据处理研究*

胡天雄,王绍宗,郭 智,冉跃龙,赵海波

(中国机械科学研究总院先进成形技术与装备全国重点实验室,北京 100083)

0 引言

近年来电子通信,航空航天领域迅速发展,采用增材制造方法实现如芯片[1]、共形天线[2-4]和先进电路[5-6]等上述领域关键零部件的快速精密制造成为行业发展趋势。现阶段多维曲面增材制造成形过程中模型数据处理效率较低,求解过程中计算复杂度较高。目前增材制造三维模型数据处理方法为:导入模型STL文件后,对模型点建立拓扑关系和哈希函数寻址以去除模型数据点冗余关系;再对所得数据排序后不断遍历以定位三角面片求解插值以确定成形运动。采用上述方法处理模型数据时,首先需单独设计函数去除数据冗余;其次在制造过程中需要不断重复遍历模型数据点进行运动规划,导致求解效率较低、过程繁琐;随着增材制造运动规划复杂度的增加,尤其采用如曲面轮廓偏移、曲面分形曲线等规划方法时,在运动规划过程中需要反复转向搜索以达成目标运动,上述传统数据点求解方法在速度方面存在不足。

为提升增材制造中模型数据处理速度、运动规划效率和面对复杂性能需求的多维曲面成形能力,MANMADHACHARY等[7]开展了人体骨骼增材制造中STL文件切片的冗余点去除以及平滑方法研究。罗国平[8]引入了基于k-d树的STL文件数据点查找方法,有效降低定位查找时间。VISPUTE等[9]通过建立高阶多边形来减少STL模型的数据冗余,加快后续模型数据处理。纪连正[10]通过对STL文件建立点面数据索引表以加速模型文件读取和运动规划数据点生成,有效解决了STL文件数据缺乏拓扑关系和冗余。CHEN等[11]基于RB树网格重构理论提出STL文件快速重构算法,可快速重构STL模型拓扑信息以去除冗余点。张应中等[12]通过建立基于半边编码的三角网络拓扑数据结构,降低了内存需求,去除了冗余数据。杨晟院等[13]通过将顶点链表变成饱和点删除减少后续需要比对的顶点,提出了一种高效STL网格重建方法。姜世阔等[14]对点云切片后拟合形成了曲面铺丝路径。王小平等[15]采用三角网格自动铺丝定角度路径规划算法,使用覆盖方法获得曲面均匀路径。综上所述,目前国内外学者通过建立点集拓扑关系去除STL文件冗余点,有效降低后续比对顶点数。但在后续多维曲面运动规划求解时仍需遍历STL文件数据集致使求解过程时间复杂度随三角面片数量增加和求解次数增加而增加,计算代价较大。

本文基于拾取三维模型表面后再拟合该表面以实现模型数据点高效定位的研究思路,开展模型表面点云拾取、神经网络曲面拟合和成形运动规划3方面研究,在拟合过程中实现冗余点去除和曲面拟合,并通过优化网络模型捕捉拓扑关系和直接定位数据点方法,实现平面到曲面的直接映射关系,降低了计算复杂度,提升了运动规划计算效率,实现了功能图案直接对应关系;并将研究结果应用于三维曲面打印模型处理过程中进行了数据处理效率的对比分析。

1 多维成形目标表面拾取

1.1 多维成形目标三维模型数据分析

STL文件为多个三角面片拼装的集合体,每个三角面片的欧式空间定义为空间三角形的3个顶点和该三角形所表示空间平面的法矢量,数据无拓扑和位置关系。

根据模型复杂度和用户自定义精度,表征同一模型三角面片的数量不尽相同。在增材制造的模型数据处理过程中面片数量、顶点冗余度以及求解过程中数据反复遍历次数等均对运动规划求解效率有严重影响。假设模型表面三角面片数量为N,则面中顶点数量约为0.5N,每个顶点被利用ti次,规划次数为times,故总计算次数为:

(1)

由式(1)可知随着计算次数和面片数量增加,模型计算复杂度大幅增加,严重影响后续路径和动作规划效率。

1.2 多维曲面成形目标表面点位数据拾取

多维曲面成形任务如大尺寸曲面单层打印、曲面喷涂、曲面焊接和铺丝铺带等,其目标对象为三维模型表面。而加载STL模型文件后所得为杂乱无序的点云数据,单层构件增材制造过程中只需关注表面点云处理无需内部点云,内部点云会极大影响拟合效果。对于此类模型,本文采用凹包围实现表面点云的快速精准提取,有效保留表面细节[16],所得结果如图3所示。

2 多维成形目标表面数据处理和运动规划

2.1 多维成形目标表面数据处理

随着计算机技术和运算架构的发展,深度神经网络具有强大的数据捕捉能力[17]。传统STL格式文件求解多维曲面运动规划需遍历所有数据以确定空间位姿,致使计算复杂度增加。由神经网络获取无固定函数的二维到三维直接映射关系可大幅提升多维曲面成形数据处理效率,在(x,y)处无附加激活函数计算关系如式(2)所示。

z=((…([x,y]·ω2×i+b1×i)·
ωi×j+b1×j)…+b1×k)·cl×1+b

(2)

式中:ωi×j表示i行j列的权重参数矩阵,b1×i表示1行j列的偏执参数矩阵,cl×1表示l行1列的输出层参数矩,通过网络模型迭代实现权重矩阵更新,以实现该点处平面倾斜度变化。本文分割曲面为多个部分分块拟合,最终将该曲面变化为由众多平面拼接而成的拼接曲面。添加激活函数后,参数矩阵更新可实现该点处面曲率变化,提升拟合度,关系如式(3)所示。

z=f(f(…f([x,y]·ω2×i+b1×i)·
ωi×j+b1×j)…+b1×k)·cl×1+b

(3)

式中:f表示某一层n个神经元的输出1行n列矩阵的矩阵输出函数。

本文基于Tensorflow框架设计多维成形目标表面拟合网络。框架第1层为点云脱壳层,用于提取STL模型表面点云;第2层为表面分割层,用于划分表面点云,进行分块拟合;第3层为刚体旋转层,用于每块点云旋转至最大投影面积,以提升拟合精度和效率;进而由10层的MLP拟合目标表面点云函数用于最终输出z轴坐标。MLP中batch_size为512,epoch为20,每层神经元模型优化器设置为‘adam’;损失函数设置为‘mse’;激活函数设置为‘relu’。在多维成形模型处理和运动规划中,根据本文模型可快速拟合目标成形表面函数,为后续曲面成形路径规划提供高效数据访问方式。

完成后模型和参数一同存储为h5文件,用于后续运动规划坐标求解,对于实际数据需要旋转归一化进入模型测试最终反归一化逆旋转得到正常输出,模型结构如图5所示。

本文数据集为STL模型中存储的n个模型数据点,前两列为训练集,后一列为标签以优化参数拟合目标表面函数z=f(x,y)。由于空间模型可能出现非函数或输出变化过于明显,导致输入相近输出变化过大,进而引起不当误差回传和参数振荡,导致模型在该数据点邻域难以收敛。故在算法初始阶段对点云进行分割和刚体旋转,求得投影面积最大角度为目标坐标系旋转角度后进行分块拟合,以使得z向聚集点铺展开来易于拟合,本文目前采用投影网格分割为等大小方块,落入同一方块为一部分进行拟合。图6中显示为一面片绕两个角点旋转角度为157°时投影面积最大,故将该点云旋转157°后投入模型训练。

φa=φ(Ta,θ)

(4)

Pa=g(Ta,θb|max(φa))

(5)

式中:Pa为旋转后点云,Ta为旋转前点云,θb|max(φa)为投影面积最大的旋转角度,旋角度为0°～180°的给定等差数组,对每次旋转均求解投影面积而后求解最大值。

2.2 多维曲面成形运动规划

采用增材制造工艺制备曲面构件的曲面模型处理过程中,曲面运动规划相较平面规划存在空间曲率变化问题,即平面驱动点距离和空间位姿点距离间存在第一型曲线积分关系。现阶段研究中针对多维成形曲面路径规划如曲面3D打印和铺丝铺带[14-15],均集中于常规横纵向切割三维模型,或是固定角度生成分层面以实现曲面路径规划,忽视了平面距离和空间距离的不对应关系,且难以实现轮廓收缩和分形曲线等曲面打印复杂路径规划方法,导致成形性能各向一致性较低;且生成路径需频繁访问模型数据集以定位周边数据点,计算代价较大。

本研究首先通过深度学习获取曲面函数,可快速定位空间点,计算代价低,效率高,可轻易实现定角度切割模型的曲面路径规划方法。而针对轮廓收缩和分形曲线路径规划方法,本文以空间球的密铺问题来表述该关系,将曲面离散为多条空间曲线,进而离散为多个空间球点的密铺,图7所示即为将一条空间曲线离散为多个等大小球的组合,在运动过程中通过对平面驱动距离的精准控制以实现空间曲面中曲线等距偏移,可有效解决平面距离和空间距离不一致的误差。

曲面运动规划中的路线偏移为递推形式,如式(6)所示。

ξk+1=ψ(ξk),k∈N

(6)

式中,ξk为第k条曲线。

运动路径ξk空间等距分割为n-1段,某点处线切向量亦为空间圆面法向量T,如式(7)所示。

(7)

ξk上某点处半径为d=2r的空间圆参数方程和空间曲面求交,找到下一曲线ξk+1上距离ξk该点处法向距离为2r的点坐标,即联立式(8)、式(9)所得为ξk+1上点。

(8)

(9)

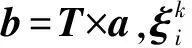
基于以上理论分析和模型构建,本文设计的算法框架如表1所示。

表1 曲面模型数据处理

3 多维成形仿真实验和结果分析

3.1 实验准备

测试环境:处理器:Intel Xeon Silver 4110,显卡:NVIDIA Quadro P4000,操作系统:Windows 10,运行框架环境:Tensoflow2.3.4,Cuda 10.1,Python 3.8。

喷墨打印作为增材制造方法的典型成形工艺,广泛应用于结构件、覆盖件等构件的快速成形及表面图案化成形。在本研究中,以喷墨打印工艺为例,选择航空航天领域的典型曲面作为目标对象验证本文模型处理方法。

在曲面成形运动规划研究方面,为测试模型求解速度,分别定位1000、10 000、100 000个随机点统计总时间后计算每点的平均定位时间。实验过程中,每组实验进行10次取其平均值;每次实验所选测试点均从区域内的2 000 000个点中随机提取,且每次实验点均不相同且点之间无任何拓扑关系。

3.2 仿真结果分析

(1)模型收敛分析。迭代学习过程中每10次全样本计算后输出一次模型采样输出情况和误差情况,如图11所示。模型拟合完成后随机定位点输出情况如图12所示,模型收敛速度较快,误差降低迅速,5次全样本计算后收敛趋于稳定。

图1 STL模型数据示意图

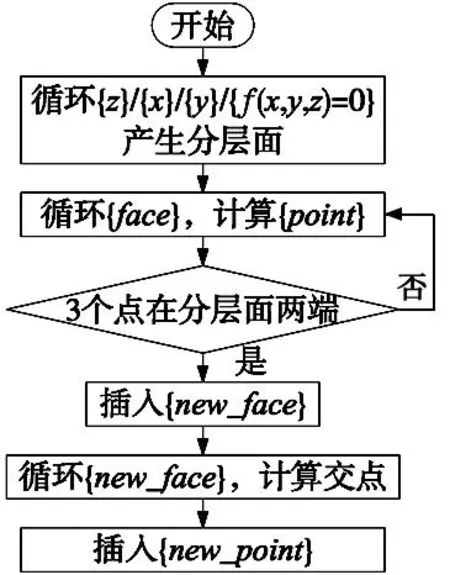
图2 STL文件求解方法常规框架

(a) 初始点云 (b) 提取表面 (c) 表面点云

(a) 无激活函数 (b) 有激活函数

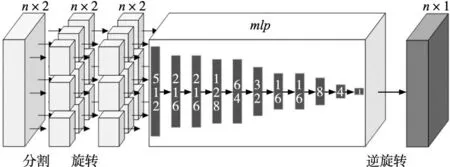
图5 本文网络模型架构

(a) 旋转0°(b) 旋转45°

图7 空间曲线微分

(a) 曲面求解 (b) 运动规划

(a) 规划三维模型 (b) 曲面规划

(a) 椭球 (b) 飞机前鼻 (c) 天线罩

(a) 椭球 (b) 飞机前鼻

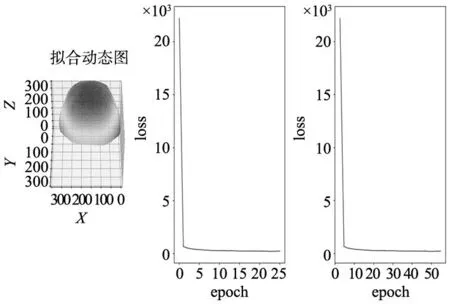
图12 头盔拟合时间和loss

(2)模型处理输出速度验证在模型处理输出速度验证时,以椭球模型和曲面天线模型[18]为研究对象,椭球模型和曲面天线基板模型顶点数分别为11 628和63 828,输出时间如表2所示,趋势如图13所示。在定位点数量为1000、10 000、100 000时椭球模型总输出时间10次实验波动范围为0.058～0.065 s、0.280～0.295 s、2.422～2.516 s;曲面天线模型总输出时间10次实验波动范围为0.061～0.069 s、0.279～0.292 s、2.496～2.534 s。由以上数据分析可知在定位点数量不变时,模型运行时间随同一模型不同次序波动较小,模型输出稳定性较高;随模型复杂度增加有略微波动。

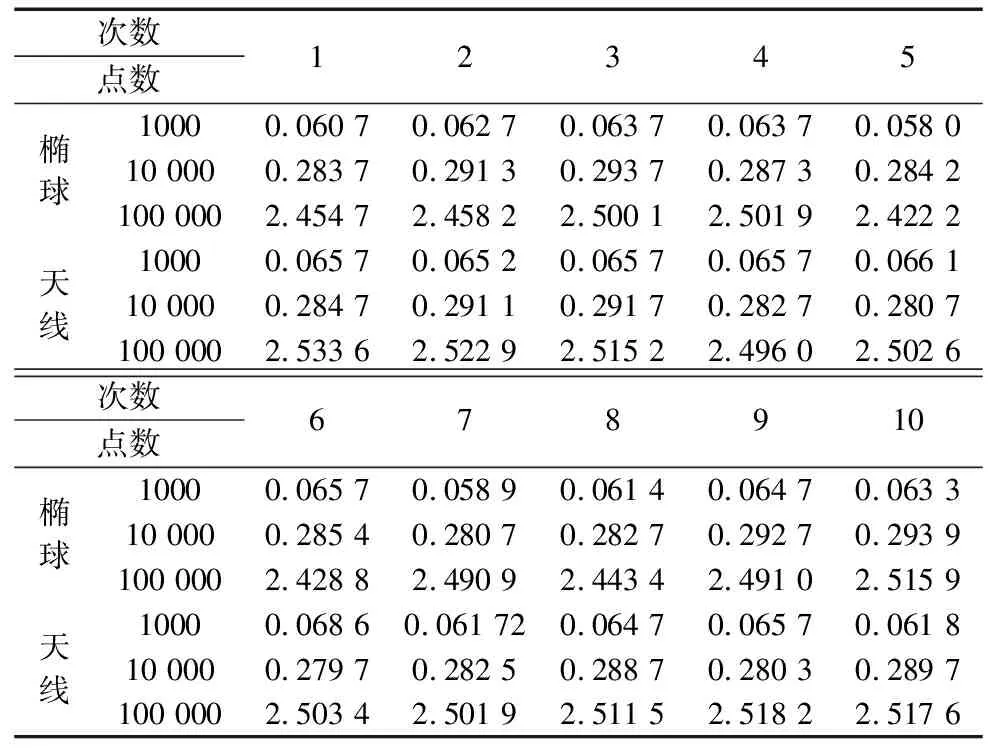
表2 椭球和曲面天线基板模型输出时间 (s)

(a) 椭球 (b) 飞机前鼻 (c) 天线罩

(a) 顶点数 (b) 定位点数

(a) 顶点数 (b) 定位点数

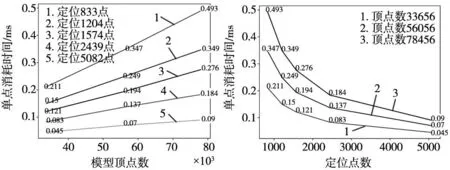
罗国平[8]研究所得如表3所示,模型顶点数一定时,单点耗时随定位点数增加而增加;定位点数一定时,单点耗时随模型点数增加而增加。

表3 罗国平研究所得STL文件数据定位算法耗时

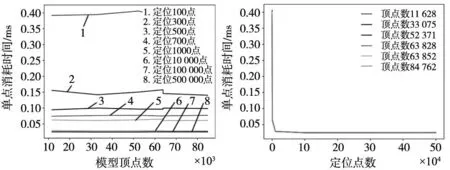
本文所得如表4所示,单点耗时在读取100点、500点、1000点、10 000点、100 000点和500 000点,模型顶点数为11 628时分别为0.391 8、0.094 6、0.062 3、0.028 7、0.024 7和0.025 1 ms;模型顶点数为33 075时分别为0.394 5、0.099 9、0.060 5、0.027 9、0.024 3和0.024 5 ms;模型顶点数为84 762时,分别为0.381 0、0.098 5、0.060 9、0.027 9、0.024 8和0.024 8 ms。相较上述STL模型定位后快速搜索的方法,本研究方法单点计算代价远低于上述方法,且本研究方法读取速度随读取点数量增加而加快,单点读取耗时迅速降低,且在大规模运动规划数据计算下计算代价降低明显,不会随模型顶点数增加而明显波动,在求解1000点时单点计算代价于0.062 0 ms上下波动,波动幅值百分比为4.9%;在求解10 000点时单点计算代价于0.028 2 ms上下波动,波动幅值百分比为2.1%;在求解100 000点时单点计算代价于0.024 7 ms上下波动,波动幅值百分比为1.9%,模型确定后定位速度趋于稳定,且模型稳定性随求解点数量增加而增强。

表4 本文STL文件数据定位时间单点耗时 (ms)

相较于现阶段其余方法,由图16可见采用数据关联性算法随着模型数据点增高而单点耗时明显增高;而其余3种方法,在模型数据点为100 000左右时,局部平衡二叉查找树(AVL)算法单点耗时为0.1 ms左右,后随着模型顶点数增加至500 000,单点定位时间逐渐增至0.5 ms左右;关联-散列算法与饱和点去除算法顶点数于100 000左右时,单点消耗时间为0.2 ms左右,且随着顶点数增加至500 000,单点耗时逐渐增加至0.173 ms和0.1 ms。本文所设计方法单点耗时在模型顶点数增加时保持稳定,且求解点数越多,单点代价越低。在模型数据量较大且顶点数大大增加时,具有非常优异的计算性能。

(a) 方法对比图 (b) 具体图

将研究所得模型设计运动规划方法应用于曲面打印路径仿真,首先读入三维模型而后调用上述网络模型求解目标曲面函数,而后调用路径生成函数,生成位姿,流程如图17所示。

图17 位姿生成方法

基于上述算法框架对航空中典型件天线罩、飞机前鼻、头盔和流形模型进行路径生成仿真,所得如图18和图19所示。

(a) 投影轮廓 (b) 平面路径 (c) 曲面路径

(a) 流形 (b) 天线罩 (c) 前鼻

最终建立整个打印设备三维模型,并且基于Python和Robostudio搭建综合模型求解,运动规划,位姿数据传输,机器人求解和运动学仿真的软件框架,仿真测试曲面打印运动求解能力,如图20所示。

图20 曲面打印典型件仿真示意图

4 结论

本文针对多维曲面成形任务中STL模型数据处理和运动规划创新设计了一种拾取模型表面点云后,通过分割、刚体旋转和拟合该曲面,进而求解运动的算法模型,仿真实验结果显示应用本方法单点求解运动点速度较传统方法提升2倍以上。

(1)单点求解时间在求解点数量从100点增加到到1000点时,单点求解时间降低约5倍;从1000点增加到到100 000点时,单点求解时间降低约2.5倍,可见单点求解时间代价随求解点数量增加而迅速降低,表明本方法在多维曲面成形空间点求解计算上可实现大规模空间点定位计算,定位点越多,代价越低;

(2)STL文件三角模型面片数量增加时,单点求解时间波动较小,且求解点数量增加后波动幅度降低,证明模型对STL文件面片数增加具有鲁棒性适用于大规模计算;

(3)本文搭建了一种模型点云处理框架,建立了二维到三维的直接映射关系,为功能图案映射,运动规划提供了有效解决方法,进而提出了一种基于体积点空间密铺的运动规划方法并进行路径生成仿真和软件运动仿真,可用于实现大型曲面焊接,曲面喷涂,铺丝铺带等应用路径生成。