基于过程测评提升教学针对性——九年级数学“微学卡”教学的实践探索

尹 晶 梁冰冰 上海市莘光学校

一、问题提出

《义务教育数学课程标准（2022 年版）》（以下简称“新课标”）比以往更加注重数学知识结构的掌握，更关注学生对数学学习过程的经历与体验。学生的学习是一个复杂的动态提升过程，如何契合数学学习经历与体验，根据教学目标重难点以及不同学生实际情况、掌握差异，跟进性地开展过程诊断与及时反馈、针对性地推进差异化教学，成为班级授课制下因材施教的突破口与关键难点。

本文指向基础教育九年级数学系统性学习提升阶段，结合教师经验积淀、课堂观察与学情分析，梳理发现该阶段数学教学的相关诊断测评主要存在如下问题与不足：

（一）忽视互动生成与策略指导，难以提升数学学习力

教师能够根据阶段检测批改情况对试卷整体情况反思，但无法关注到所有学生的订正情况，更无法实现过程跟进、互动反馈、及时指导，优化学习策略，提升学生数学学习力。

（二）测评内容范围广，难以突出数学知识主干

九年级数学知识内容覆盖面广、难度大，重视知识、技能和素养提升。然而目前的各类测评，更多聚焦在各类各样的知识点，未能凸显主干知识脉络，不能及时发现学生的知识漏洞，也难以抓住关键易错点进行针对性的变式训练。

（三）测评实施跨度长，难以助推数学思维发展

基础教育阶段的数学学习时间跨度较长，九年级阶段的数学测评频繁、指向杂多，但常常缺乏结构化梳理，缺少从知到会的能力水平台阶，往往难以促进学生思维发展和提升。

（四）评价结果局限于数学分数，学生缺乏热情和内驱力

当下数学教学检测结果主要是对学生的量化评价，或给予一个固定的分数或划分为不同的等级，难以反映不同学生的学习基础、差异和进步情况，甚至导致一些学生对数学学习畏惧不前、自信心下降，缺乏主动学习的热情和内驱力。

面对这些情况，教师亟需深入不同学生的不同学习过程进行深入诊断、及时反馈与针对性辅导提升，借助有效方式方法，以此充分激发学习情意、聚焦关键主干，不断优化认知结构，提升策略与数学学习素养。

二、借鉴卡片式学习开展“微学卡”设计

在破解上述难题过程中，我们探索发现：“卡片式学习”是班级统一教学下开展差异化教学的有效路径；卡片作为最小记忆单位，能降低识记负担，提升针对性诊断、练习与辅导、指引，并在20 世纪初就得以有效应用。在此，借鉴“卡片式学习”的实践研究，借助“闵智作业”平台资源，特开展九年级数学“微学卡”教学实践探索。它主要基于“闵智作业”平台，对学生个体、班级进行较大范围的数据分析，运用教学实践智慧将集中性错题进行整理，大大地提高效率。不同于以往研究的卡片式学习通常用于课堂教学中，本研究的“微学卡”主要致力于课后诊断，形式上包括无关联练习、变式练习、自命题练习、周期练习及开放性练习五类；内容上指向核心知识点、关键问题链、典型数学模型等，更加精准地跟进分析学生的差异性，更加精确、及时地开展反馈指导。其主要设计路径如图1所示。

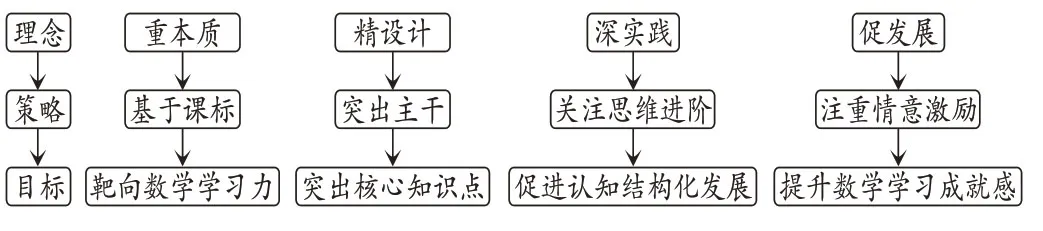
图1 “微学卡”的设计路径框架示意图

三、“微学卡”数学教学的实践探索

（一）重本质：基于新课标，靶向数学学习力

新课标指出学生是学习的主体，教师是学习的组织者、引导者与合作者。每一张微学卡由教师厘清题目类型，涉及一种方法或几个知识点，其中的练习题都选自平时作业题、书本例题或变式练习等。几张微学卡的知识点可以建构知识间的联系，有助于学生思维逻辑体系化，提升解决问题的能力。微学卡的下方配有数学名人名言，激励学生不断发现问题、解决问题，用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界。

（二）精设计：突出主干，聚焦数学核心素养

新课标指出课程内容选择符合学生的认知规律，有助于学生理解、掌握数学的基础知识和基本技能，形成数学基本思想，微学卡针对学生近期学习的难点和混淆点，教师结合班级学情，制定并不断调整微学卡的内容和格式。微学卡制作初期，内容来源于“闵智作业”中学生日常作业的错题，是没有关联的，实践过程中笔者发现学生只是机械模仿，不能灵活运用，因此笔者在原题的基础上进行变式，使学生达到举一反三的目的，同时，笔者鼓励学生自己对题目进行改编，开拓学优生思维（如图2所示）。

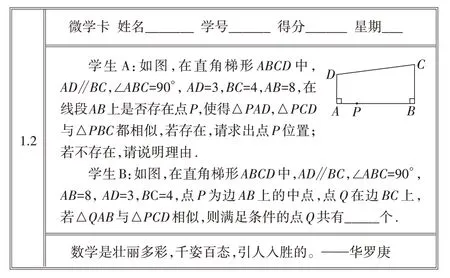
图2 微学卡版本进阶

案例1

微学卡1.0：如图，已知△ABC中，点D在边AC上，AB=12，AC=8，AD=6.当点P在边AB什么位置时，△ADP与△ABC相似？

微学卡1.1：如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为边AB上一动点，若△PAD与△PBC相似，则满足条件的点P共有__个。

微学卡1.2：学生A：如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AD=3，BC=4，AB=8，在线段AB上是否存在点P，使得△PAD，△PCD与△PBC都相似，若存在，请求出点P位置；若不存在，请说明理由。

学生B：如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为边AB上的中点，点Q在边BC上，若△QAB与△PCD相似，则满足条件的点Q共有_______个。

上述微学卡1.0 题目来自练习册第15 页点P为边AB上有两种情形，可得满足条件的点P共有3个。根据批改数据，此题学生掌握情况良好，因此教师在错题复做的基础上再次进行变式训练，将上述微学卡1.0 中的“点P为边AB上一动点”变为“点P为直线AB上一动点”得到微学卡1.1，则又出现当点P在BA延长线上和点P在AB延长线上两种情形，故满足条件的点P共有5个。让学生自主命题产生微学卡1.2，有学生将“点P在直线AB上”变式为“点P为边AB上的中点，点Q在边BC上”，“点P、Q分别为边AB、CD上的动点”等进行探究，使学生的数学思维得到了极大的提升。

（三）深实践：关注思维进阶，促进认知结构化发展

新课标指出课程内容的组织重点是对内容进行结构化整合，探索发展学生核心素养的路径。重视数学结果的形成过程，处理好过程与结果的关系。

基于教、学、评一体化原则，随着题目难度增大，学生完成题目的时长增长，多道题的微学卡不能达到及时反馈的目的，笔者将微学卡由以天为周期改成以周为周期。举例如下：

案例2

星期一 如图，直线y=-x+3与x轴、y轴分别交于点A、B，抛物线y=ax2+bx（a≠0）经过点A，

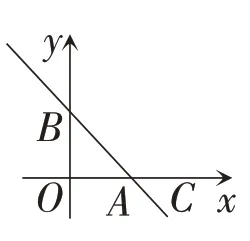
（1）当顶点D在直线y=-x+3上，求a的值。

（2）当顶点D位于△AOB内，求a的取值范围。

星期二 直线y=-x+3 与抛物线y=-x2+bx+c经过点A、B，平移这条抛物线，所得新抛物线的顶点为P（m，n），如果PO=PB，且新抛物线的顶点在△AOB内，求m+n的取值范围。

星期二 直线y=-x+3与x轴、y轴分别交于点A、B，抛物线的方程为y=-x2+2x+3，G为抛物线的顶点，P为线段AB上的点，且点P的横坐标为m。过P作y轴的平行线交抛物线于H。若顶点G在以PB、PH为邻边的平行四边形的形内（不含边界），求m的取值范围。

星期四 直线y=-x+3与x轴、y轴分别交于点A、B，抛物线的方程为y=-x2+2x+3，设抛物线上点F的横坐标为n，将抛物线向左平移2个单位，如果点F的对应点F′落在△AOB内，求n的取值范围。

星期五 直线y=-x+3与x轴、y轴分别交于点A、B，抛物线的方程为y=-x2+2x+3。

（1）若抛物线的方程变为y=ax2-2ax-3a（a＜0），其顶点为Q，若Q在△AOB内，求a的取值范围。

（2）设抛物线上点G的横坐标为k，将抛物线向右平移2 个单位，如果点G的对应点G′落在△AOB内，求k的取值范围。

本周微学卡由中考题出发进行变式，问题的设计让学生在知识层面逐步推进，充分理解二次函数背景下字母取值范围问题：1.点动→找轨迹→求出点坐标→联立方程（组）、不等式（组）→得到字母系数范围，2.图形运动→找临界位置→求出点坐标→联立方程（组）、不等式（组）→得到字母系数范围，让学生找准知识“生长点”，将这部分数学知识串联成线，感受数学知识的逻辑连贯性，体会数学的逻辑美，同时在学生掌握基础知识的前提下笔者也尝试设计开放式问题的探究性微学卡。

（四）促发展：注重情意激励，提升学习成就感

新课标指出，评价不仅要关注学生数学学习结果，还要关注学生数学学习过程，并鼓励采用多元的评价主体和多样的评价方式，鼓励学生自我监控学习的过程和结果。

在实施微学卡过程中，建立量化评价表，组建积分小组，能对学生使用微学卡的成效进行评价。在微学卡的使用中，还需家长参与其中，发表见解，让学生的有效学习得到多方面的及时反馈，从而提升学生学习数学的成就感和喜悦感。

四、成效与思考

（一）实践成效

“微学卡”的实践探索旨在通过“闵智作业”平台与教师实践智慧相结合，从本质上改变学习模式在班级授课制下根据不同学生、不同学习阶段的具体情况有效开展差异化教学。经过近一年的实践，取得了显著实践成效。

1.提升了学生数学学习力

微学卡的设计与开发，主要基于数学课程标准，靶向学生的数学学习策略，通过差异化目标、内容和过程，及时反馈并指导数学学习策略，有效提升了学生数学学习力。

案例3

微学卡：如图，已知抛物线y=-x2+bx+c经过点B（-3，1），点D（5，5），直线BD交x轴于点A，交y轴于点C，联结OB、OD.

（1）根据这些条件你能得到什么结论？

（2）是否存在点E，使得△ODE与△BCO相似？若存在，求出E点的坐标；若不存在，请说明理由。

学生1视角：点E在坐标轴上。

学生2视角：点E在函数图像上。

学生3视角：点E在象限内。

学生4视角：点E在坐标系内。

学生思考的视角不同，题目的难度也就不同。学生用几何法或代数法多角度、多层次地思考，添加不同的条件呈现不同的解题方法，总结平面直角坐标系背景下相似三角形的解题策略，即固态三角形→动态三角形中有一组定角→动态三角形中无定角时两个三角形相似的判定策略，展现了学生思维的灵活性和独创性，数学的逻辑推理、几何直观、运算能力等核心素养都得以提升。从以上探究式微学卡的反馈中发现，学生的思维更加灵活，探究问题和创新意识更强，呈现了很多教师预设以外的效果。（如图3所示）

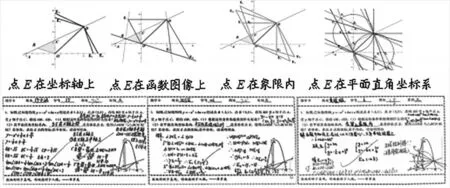
图3 学生的不同视角

2.提升了教师专业素养

如上实践探索，提升了学生数学学习成效，促进了教师的互相协作，发挥了团队智慧：学校初步建立了九年级微学卡库，同时围绕“微学卡”营造了钻研、交流的教研氛围，促进了教师专业素养的提升。

（二）后续思考

本文主要是在“双减”背景下，基于“卡片式学习法”和现阶段的课后诊断方式进行探究，微学卡有助于九年级数学课堂的优化，能及时反馈，促进评价，提高学生学习数学的自驱力，提升学生的数学素养。为持续提升微学卡的成效，后续将对微学卡的高效使用与优化、系列设计与推进以及智能分析与推送着重研究与探索，力求实现数据驱动下的“以学定教、精准施教、以评促教”，真正实现减负增效。