大负荷抢修作业机械臂误差拆分补偿控制方法设计

张 伟，张景明，窦金龙，白永刚

（国网山东省电力公司东营供电公司，东营 257000）

大负荷抢修作业机械臂具备强大的承载能力、高度灵活的运动能力以及精确的控制系统，专门设计用于承担重负荷并进行紧急维修和救援任务[1]。这种机械臂具有很高的操作性能和可靠性，能够承受巨大的压力和负荷，同时具备精确控制能力，可以根据不同任务的需求进行灵活调整和操作。通过机械臂的使用，可减少人工劳动的危险性，提高工作效率和安全性。但该机械臂受到的负荷较大，导致机械臂控制全过程姿态同步性较差。为此，需要研究一种机械臂的误差补偿控制方法。

针对当前机械臂控制效果较差的问题，在机械臂轨迹控制补偿方面已开展多项研究。文献[2]结合Lagrang 法与Morison 方程完成机械臂动力学模型的构建，通过RBF 神经网络优化机械臂动力学模型参数，采用模糊控制方法，对机械臂的运动实施补偿。文献[3]建立机械臂约束控制系统，通过奇异摄动法对机械臂控制控制系统实施柔性控制，并采用U-K 法对机械臂运动状态展开跟随控制，通过机械臂约束条件下的系统误差收敛方法，实现机械臂的补偿控制。文献[4]建立机械臂动力学模型，计算机械臂实际运行轨迹与期望运行轨迹之间的误差，结合RBF-BP 算法，实现机械臂的补偿控制。但上述方法在控制机械臂的过程中，仍存在机械臂容易受到意外的碰撞或摩擦，使其实际运动轨迹与目标轨迹存在偏差的问题。

为了解决上述方法中存在的问题，本文提出大负荷抢修作业机械臂误差拆分补偿控制方法。针对机械臂控制过程姿态同步性较差的问题，建立抢修机械臂运动结构，计算大负荷机械臂空间约束条件，提高机械臂控制精准度。将大负荷机械臂轨迹误差分解为不同的分量，利用前馈+PD 控制器补偿误差分量，提高机械臂的控制效果。

1 大负荷机械臂的约束与误差分析

1.1 大负荷机械臂空间约束条件计算

通过计算空间约束条件，可以确定机械臂在特定位置和姿态下的运动范围，避免运动冲突和碰撞，确保机械臂能够安全、准确地完成任务。机械臂的简化连杆运动结构如图1 所示。

图1 抢修机械臂运动结构Fig.1 Movement structure of emergency repair robotic arm

图中D1、D2、D3为抢修机械臂连杆构成的几何参数，ϑ1、ϑ2、ϑ3分别为抢修机械臂回转机构转角、大臂转角以及小臂转角。在D1、D2、D3、ϑ1、ϑ2min、ϑ2max、ϑ3min、ϑ3max机械臂运动空间参数已知的前提下，可确定机械臂末端端点P 的空间位置。设P（x，y，z）为机械臂端点位置坐标，P（x，y，z）的位置参量x，y，z为

观察图1 可发现，抢修机械臂在xoy 二维平面内存在4 条投影边界曲线，分别为P1P2、P1P4、P2P3、P3P4，4 条边界曲线的交点为P1（x1，y1）、P2（x2，y2）、P3（x3，y3）、P4（x4，y4），通过计算4个圆弧半径的最小值，可以确定机械臂在满足各种位姿要求的前提下，能够到达的极限位置，即最大作业空间。其约束条件为

式中：R1，R2，R3，R4为4条投影边界曲线的圆弧半径。求解4 条圆弧，即可获取大负荷机械臂空间约束条件。

1.2 大负荷机械臂轨迹误差可分性分析

一般来说，轨迹误差是由多种因素引起的，如果能够将轨迹误差因素分解为不同的分量，如机械臂动能、机械臂势能、机械臂广义力分量等。以此可以针对每个分量实施补偿，从而提高机械臂的轨迹精度。将抢修机械臂作业过程中，机械臂随机关节以及关节连接的连杆视作一个动力单元，设抢修机械臂作业过程中，机械臂第n 节连杆的第l 个单元质心在作业空间内产生的动能为El、势能为Eq，引入拉格朗日算法[5]对机械臂动力学模型展开构建。引入大负荷机械臂空间约束条件，建立拉格朗日基本方程：

式中：Sj为第j 个单元的广义力；γj为机械臂质点位移为γj对应的广义速度。

（1）机械臂动能分量

设机械臂第n 节连杆的第l 个单元质心对应的作业空间边界弧长为tnl，将单元质心l 对应到抢修机械臂作业空间的坐标系中，设此时单元质心l 的坐标为snl，此时质心所在连杆的动能Enl为

式中：mnl为质心l 所在第n 节连杆的质量；vnl为速度。结合拉格朗日基本方程，对抢修机械臂上多段连杆驱动下的机械臂动能分量展开推导，推导结果为

式中：I 为对称正定矩阵[6]；N 为机械臂连杆总量；γ¯l为机械臂广义速度。

（2）机械臂势能分量

设机械臂第n 节连杆的转角为ϑn，结合拉格朗日基本方程，机械臂第n 节连杆势能为

式中：E1、E2为机械臂弹性杆弹性模量以及机械臂驱动线弹性模量；H1、H2为机械臂弹性杆惯性矩与机械臂驱动线惯性矩。多段连杆构成的机械臂势能分量Eq为

（3）机械臂广义力分量

抢修机械臂作业过程中，由于机械臂的弯曲，中心弹性杠杆以及杠杆驱动线呈同一角度弯曲，设Af、Al分别为机械臂连杆作业过程中雅可比矩阵以及驱动线雅可比矩阵[7]，则机械臂的广义力分量为

式中：D 为驱动线的驱动力总和；ξ 为抢修机械臂末端的外力施加总和。

通过机械臂动能、势能、广义力三方面分析[8]，结合达朗贝尔原理，可得到大负荷机械臂轨迹误差方程为

2 机械臂误差拆分补偿控制方法

在上述研究中，将大负荷机械臂轨迹误差因素分解为机械臂动能、机械臂势能、机械臂广义力分量。针对每个误差分量，引入前馈+PD 控制器，补偿拆分后的轨迹误差分量，以实现精准的轨迹控制。在笛卡尔空间内对抢修机械臂作业轨迹[9]展开分析，如图2 所示。

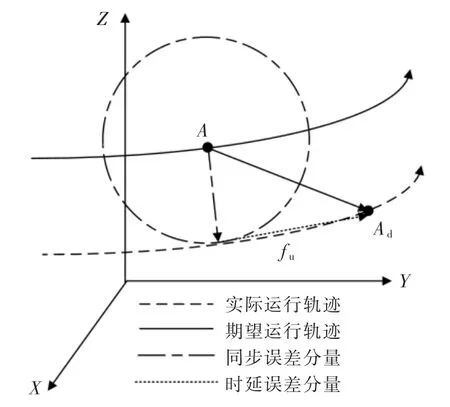
图2 笛卡尔空间同步误差度量Fig.2 Measurement of synchronization error in Cartesian space

图2 中点A 为抢修机械臂在第二空间运行过程中随机时间点t 的机械臂实际运行位置，Ad为给定期望运行轨迹中机械臂在t 时间点的期望运行位置。在此基础之上，引入前馈+PD 控制器[10]对机械臂运行过程中的机械臂动能分量、机械臂势能分量和机械臂广义力分量误差展开补偿控制。设F 为抢修作业机械臂运行轨迹误差与同步误差的等价补偿量，μ 为同步误差补偿系数，推导+PD 控制器的补偿控制律σ，实现机械臂误差拆分补偿。

3 实验与分析

实验在一个5 m×5 m 的方形区域模拟实际的大负荷抢修作业环境，采用FSS-16-500N-50 力传感器实时采集大负荷抢修作业机械臂在运行过程中的数据，该传感器的采样频率为50 Hz、分辨率为0.1 N。

实验所用的机械臂为一个大负载、高精度的工业机械臂，该机械臂具有6 个自由度，可以实现在三维空间中的精确运动。在实验中，机械臂需要完成一系列复杂的曲线轨迹运动。实验现场如图3所示。

图3 实验现场图Fig.3 Experimental site map

3.1 运行轨迹误差拆分效果分析

在大负荷抢修作业机械臂误差拆分补偿控制方法设计中，轨迹误差拆分的意义在于将复杂的机械臂轨迹误差分解为多个独立的分量，每个分量代表特定的误差来源或运动特性。这种拆分方法有助于更好地理解和控制机械臂的轨迹精度。拆分运行轨迹误差结果如图4 所示。

图4 运行轨迹误差拆分效果Fig.4 Split effect of running trajectory error

由图4 可知，机械臂在运行过程中，P1、P2、P3、P4和P5处存在误差，而利用所提方法可以清晰地将轨迹误差分解为多个独立的分量，具有良好的误差拆分能力。

3.2 运行轨迹控制效果分析

为了验证所提方法的可行性，设定一条抢修机械臂运行期望轨迹，所提方法的补偿控制效果如图5 所示。

图5 运行轨迹控制结果Fig.5 Running trajectory control results

观察图5 可发现，所提方法补偿控制下，抢修机械臂的运行轨迹与期望运行轨迹较接近，表明该方法的运行轨迹控制效果好。

3.3 位姿角偏移分析

在上述实验基础上，选取随机时段的抢修机械臂运行参数作为实验样本，分析抢修机械臂实际运行过程中的姿态角偏移情况，如表1 所示。

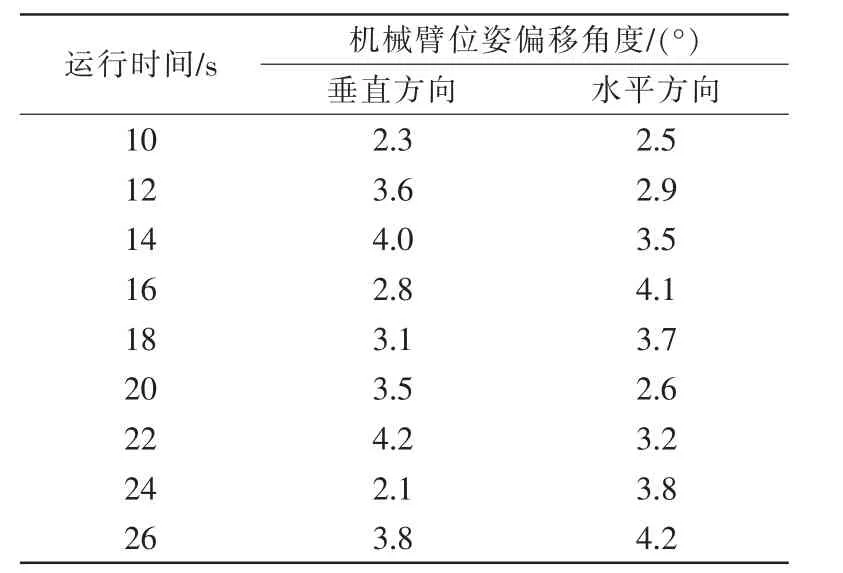
表1 位姿角偏移情况Tab.1 Posture angle deviation

分析表1 可知，利用所提方法对抢修机械臂展开自适应补偿控制后，机械臂水平方向与垂直方向的位姿偏移角均控制在4.2°以下，偏移程度小。这是因为所提方法基于抢修机械臂整体结构，对机械臂的最大运行范围展开了二维空间映射，确定了机械臂的实际工作空间，进而达到了机械臂运行过程精细化分析目的，优化了后续机械臂控制精度。

3.4 控制稳定性分析

在已知抢修机器人机械臂存在大幅度偏移前提下，对机械臂残余振动展开测量，测量结果如图6所示。

图6 机械臂残余振动测量结果Fig.6 Residual vibration measurement results of the robotic arm

观察图6 可发现，所提方法在对存在运行轨迹偏移的抢修机械臂展开自适应补偿控制期间，机械臂参与振动幅度较小，机械臂整体运行较为平稳。这是因为所提方法拆分了动能、势能、广义力分量，并对差分的分量分别实施补偿，因此实现了机械臂的高稳定性控制。

4 结语

为了进一步提高大负荷抢修作业机械臂控制效果，将抢修机械臂简化后的连杆运动投影至二维平面后，获取机械臂的简化连杆运动结构，以此计算机械臂空间约束条件。从动能、势能、广义力3 个角度分析轨迹误差可分性，基于笛卡尔空间分析机械臂的作业轨迹，通过前馈+PD 控制器对机械臂的机械臂动能分量、机械臂势能分量和机械臂广义力分量误差实施补偿，为抢修机械臂的精准作业提供保障。