基于模糊解耦的坩埚下降法晶体生长炉温度控制系统

陈祥烨，王森林，陈 豪

（1.福州大学 电气工程与自动化学院，福州 350000；2.中国科学院海西研究院泉州装备制造研究中心，泉州 362000）

使用坩埚下降法生长晶体通常需要两个温区[1]，分别为上温区与下温区，它们同时影响炉体内温度的分布。根据热力学分析，炉内热量上升并聚集到高温区，使得高温区的升温速率加快，将会出现高温区易超调的现象[2]，而低温区离炉底较近，密闭性较差，散热严重，且两个温区之间没有隔离装置，因此晶体生长炉温控系统是一个典型的多输入多输出、强耦合性的系统[3-4]。如何对耦合系统进行精准控制一直是学者和工程人员讨论的热点问题，传统的控制方式是采用常规PID 算法[5]对多变量耦合系统进行控制。虽然本系统最终可以收敛至目标值，但动态性能和鲁棒性较差，已无法满足需求。为了解决这个问题，国内外学者和工程师的思想是通过把多变量系统解耦成单变量系统进行分次控制。现有的解耦设计方法主要分为传统解耦法、自适应解耦法和智能解耦法等三大类[6]。传统解耦法主要是基于矩阵运算将多输入多输出系统转变为对角线形式，从而实现解耦。文献[7]使用矩阵解耦理论实现对精馏塔耦合系统温度的精准控制，但该方法过于依赖被控对象的精确数学模型，不适用于像晶体生长炉这样的非线性时变系统。随着神经网络技术的流行，学者们也提出了自适应解耦法。例如，文献[8]通过基于神经网络的PID 控制算法实现了对多输入多输出系统的解耦，该方法使得系统具有很好的自学习特性，但存在收敛速度过慢的问题；文献[9]在其基础上进行改进，提出分数阶的神经网络解耦方法，提高了BP 神经网络的收敛速度，保证了系统具有良好的动态性能与控制精度，但由于采用在线辨识对象的数学模型进行控制，因此存在算法复杂、计算量庞大等问题。相比之下，智能解耦法对此类系统具有独特的优势，其中模糊解耦方法是一种实用的方法[10]，文献[11]将模糊PID 算法应用于温室大棚中，证明了其各项动态指标均优于PID 算法，但仍存在超调过高，调节时间长等问题；文献[12]采用了模糊PID 算法与传统解耦方法相结合的方式应用于工业燃烧炉中，仿真波形几乎不存在超调，调节时间短，且鲁棒性较好，但存在计算量较大的问题。

本文针对坩埚下降法晶体生长炉温度控制系统，设计了模糊解耦控制器，并对坩埚下降法晶体生长炉系统进行了仿真。仿真结果表明，采用模糊解耦算法的控制效果优于传统PID 算法与传统解耦算法，系统具有很好的动态性能与鲁棒性。

1 模糊解耦控制系统设计

1.1 模糊解耦控制系统组成

为了解决PID 算法难以控制MIMO 系统的问题，以及传统解耦算法对于被控对象精确数学模型的依赖，本文设计了模糊解耦系统，如图1 所示。其中模糊解耦控制器的控制流程如图2 所示。

图1 模糊解耦控制系统Fig.1 Fuzzy decoupling control system

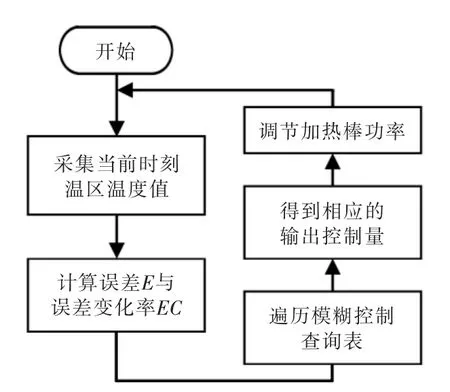
图2 模糊解耦控制器控制流程Fig.2 Fuzzy decoupling controller control flow chart

1.2 模糊化

将上温区的目标值与实际温度值的偏差E1以及偏差变化率EC1作为模糊解耦控制器的输入，将温控器输出功率作为输出。根据上温区温度的控制要求，E1与EC1的量化论域为［-6，6］，其对应的模糊词集为｛NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）｝，上温区加热棒的输出功率U1为0～100%，其量化论域为［0，0.2，0.4，0.6，0.8，1.0］，模糊词集为｛NB（负大）、NM（负中）、NS（负小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）｝[13]。下温区变量E2、EC2、U2的量化论域与模糊词集同上温区，所有变量均选择三角形隶属度函数。

1.3 构建模糊规则表

本文结合操作人员对晶体生长炉操作经验，得出上温区温度模糊控制规则表与下温区温度模糊控制规则表，具体如表1 和表2 所示。模糊控制规则表直接构成了阐述晶体生长炉温度控制系统的模糊算法。

表1 上温区温度模糊控制规则Tab.1 Temperature fuzzy control rule in upper temperature region

表2 下温区温度模糊控制规则Tab.2 Temperature fuzzy control rule in lower temperature region

1.4 模糊推理

本文选用Mamdani 模糊推理法[14]，通过时刻模糊控制器的输入变量量化值获取隶属度值，结合晶体生长炉实际生产过程中的控制特点，得到上、下温区温度模糊控制查询表，具体如表3 和表4 所示。

表3 上温区温度模糊控制查询表Tab.3 Query table for temperature fuzzy control in upper temperature region

表4 下温区温度模糊控制查询表Tab.4 Query table for temperature fuzzy control in lower temperature region

2 仿真实验

2.1 数据采集

在炉内温度为室温的条件下，分别对上、下温区施加相同的阶跃信号单独起炉，同时对2 个温区每隔1 s 影响温度上升数值进行采集，部分数据如表5、表6 所示。

表5 上温区单独起炉Tab.5 Separate heating in upper temperature zone

表6 下温区单独起炉Tab.6 Separate heating in lower temperature zone

2.2 系统辨识

一般情况下，工业燃烧炉温度控制对象可近似为带滞后的一阶惯性环节，其传递函数表达形式为[15]

式中：K 为增益系数；T 为时间常数；τ 为延迟时间。

利用系统辨识工具箱[16]对上述数据进行辨识，得到相关的参数，最终可得晶体生长炉温度控制系统的传递函数为

2.3 阶跃响应对比

为了对比3 种控制算法的阶跃响应表现，在上温区输入给定700℃，下温区输入给定500℃的基础上进行仿真，系统的稳态对比如图3、图4 所示。

图3 上温区700℃响应图Fig.3 Response diagram of upper temperature region at 700℃

图4 下温区500℃响应图Fig.4 Response diagram of lower temperature region at 500℃

统计稳态响应下3 种不同控制算法实验结果，如表7 所示。

表7 上、下温区仿真分析对比分析表Tab.7 Comparison analysis table of upper and lower temperature zone simulation analysis

结果表明，采用模糊解耦PID 算法和传统解耦PID 算法均能实现无超调，但模糊解耦PID 算法在调节时间上有明显的优势，可见采用模糊解耦PID算法系统会具有更好的快速性。

2.4 过程扰动测试

为了对比3 种算法的抗干扰性能，在稳态的基础上加入过程扰动进行仿真，得到的仿真波形图如图5、图6 所示。

图5 上温区过程扰动响应Fig.5 Process disturbance response diagram in upper temperature region

图6 下温区过程扰动响应Fig.6 Process disturbance response diagram in lower temperature region

可以看出，相较于PID 算法与传统解耦PID 算法，采用模糊解耦PID 算法在遇到过程干扰时可以更加平稳快速地控制系统运行，表现出更好的抗干扰性能。

2.5 模型失配测试

保持各控制器参数不变，将被控对象传递函数的时间常数T 与增益K 增加40%，系统模型失配40%时，先分别给定上、下温区700℃和500℃的输入信号，并在系统稳态后加入过程扰动，3 种算法的响应曲线如图7、图8 所示。

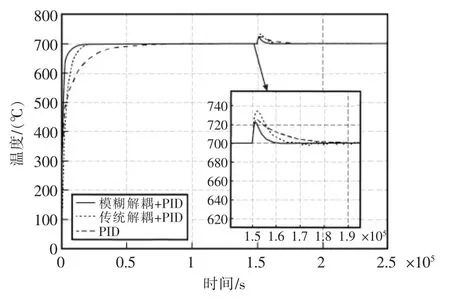
图7 上温区模型失配时仿真对比曲线Fig.7 Simulation comparison curve when the upper temperature zone model is mismatched

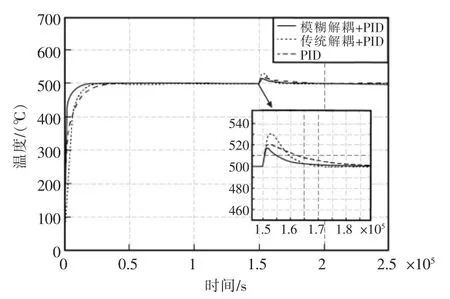
图8 下温区模型失配时仿真对比曲线Fig.8 Simulation comparison curve when the lower temperature zone model is mismatched

可以看出，当模型失配40%时，采用PID 算法时超调时间过长无法满足实际需求；采用传统解耦PID 算法时由于系统参数发生了变化，系统一直处于震荡状态，无法收敛。而采用模糊解耦PID 算法，系统超调量无变化，调节时间变化幅度不大，可见基于模糊解耦PID 算法较其他两种算法对被控对象参数的变化具有更强的适应能力，这体现了模糊解耦控制的最大特点就是不依赖被控对象的精确数学模型，当被控对象的参数在一定范围内变化时，对系统的动态性能影响不大。

3 结语

本文对坩埚下降法晶体生长炉温度控制系统，针对PID 算法与传统解耦PID 算法所存在的动态性能较差、抗干扰性能较弱、严重依赖被控对象的精确数学模型等问题。在传统解耦控制算法的基础上进行改进，提出了模糊解耦PID 算法，通过仿真分析，相较于PID 算法与传统解耦的PID 算法，模糊解耦算法在超调量、动态性能、抗干扰性、系统运行稳定性上表现优异，同时面对被控对象参数的变化也具有很好的适应能力，本方法较为简单实用，可以广泛应用于晶体生长炉的控温过程。