二元混合物在液体层上发生马兰戈尼爆裂的研究

谢科薇 陶金成 董裕力 翁雨燕 杨俊义 方亮

(苏州大学物理与科学技术学院,苏州 215031)

由于马兰戈尼效应,液滴在液体层表面自发铺展成薄膜的物理过程,在成膜技术、涂层工艺、以及纳米器件的制作等领域具有广泛的应用,但是铺展后液膜自发碎裂成小液滴的现象也被广泛观察到,这种现象限制了马兰戈尼效应应用的发展.本文基于以往的实验观察对液膜的碎裂机制进行完备的解释,并通过实验进行验证,指出了液滴薄膜中心与边缘蒸发速率的差异引起的马兰戈尼流动对液膜边界产生的微扰,使得液滴铺展到最大时边缘生长出指状液柱.此外,根据微扰模型推导出边界失稳的临界波长和最大波长的表达式,基于Plateau-Rayleigh 不稳定性解释了指状液柱碎裂的原因.建立同心圆柱壳液柱模型简化计算,预测了不同黏度比的液滴在液体层上铺展为薄膜的浓度范围和发生马兰戈尼爆裂的位置区间,并通过实验验证了不同醇溶液发生马兰戈尼爆裂的浓度范围和位置区间.该理论解释将在成膜技术、涂层工艺等领域提供更加精细的理论指导;特别地,本文提出的同心圆柱壳简化模型为化工领域微量反应和纳米颗粒制备等研究领域中的一些技术难题提供新的解决思路.

1 引言

当一滴二元混合物(如水-乙醇)滴落在疏水性液体(如油)的表面时,漂浮在油层表面的母液滴有时会散开碎成更小的液滴,这个现象被称为马兰戈尼爆裂.本文将对这一现象进行详细的分析,该现象可以分为两个阶段: 阶段1 是液滴润湿液体层,在马兰戈尼效应[1]的作用下铺展为薄膜,达到最大的扩散半径;阶段2 是在薄膜扩散到最大时,内部未停止的马兰戈尼流使得边界产生了指状液柱,又因为Plateau-Rayleigh 不稳定性的存在,生长到一定长度的指状液柱碎裂形成小液滴,最终整个液膜破碎发生马兰戈尼爆裂的现象.

液滴可以自发在液体层铺展成薄膜的优良性质让马兰戈尼效应在半导体成膜[2]及纳米器件的制作[3]等方面被广泛应用,正是因为巨大的应用前景液体表面的Marangoni 铺展问题被大量研究.从1969 年Fay[4]研究了石油在水面上的铺展,首次建立了液滴铺展半径与时间的幂指数关系后,到1980 年,Huh 等[5],Foda 和Cox[6]采用更严谨的数学推导验证Fay 的结论,详尽地研究了液滴在水面上铺展的力学机制.之后的几年,一维射流的不稳定性首先被观察到,并被广泛研究[7,8],例如1983 年Smith 等[9,10]详细讨论射流的表面波、对流不稳定性.但随着研究和应用的进一步发展,1988—1998 年二维液膜自发碎裂成小液滴的现象逐渐在不同实验中被观察到[11-17],其中导致马兰戈尼流而引起不稳定的因素包括: 溶液浓度变化(蒸发)[11-15]、温度变化(热驱动)[16]、表面活性剂[17]等,自此液膜不稳定性方面的研究也分为了以上3 个主题.由于液膜的破碎限制了马兰戈尼效应的应用,进入21 世纪,相关问题被广泛研究,在液膜扩散[18]、边缘润湿[19]、液柱断裂[20]、边缘碎裂[21]、指状液柱形成[22]等现象都有相关研究.不过相比于第1 阶段完备的理论,对第2 阶段扰动和不稳定的分析例如上述研究都主要是实验研究.特别地,Hernández-Sánchez 等[23]根据实验得到液体层表面上液体的驱替铺展由界面张力梯度主导.但Huh 等[5],Foda 和Cox[6]的研究表明液滴在边缘处界面张力已经达到平衡,并不会在边缘处长出小液柱,也正是因为这样的悖论让液滴边界失稳的原因一直没有理论进行解释.此外对于生长出的液柱最终碎裂成为小液滴的原因,大量的实验文章推测是由于Plateau-Rayleigh 不稳定现象[21,24,25],但是由于液柱在液体表面流动而导致的上下不对称边界条件,让Plateau-Rayleigh 不稳定扰动下液柱的流动方程复杂到无法求解.

针对上述问题,本文将根据液液界面的自由能理论推导出二元混合物在液体层表面实现铺展的关系式,代入希斯科夫斯基公式计算出短链醇溶液在油层表面铺展为薄膜的浓度范围.完全铺展后液滴内部的马兰戈尼效应依旧存在,引起了液滴边界的不稳定性.本文将扰动表示为一个无限的波函数叠加,结合杨拉普拉斯方程对扰动下液滴的速度势方程,求解得到了发生失稳的临界条件与失稳后液柱生长时对应的波长.经过分析可知醇溶液在液体层表面铺展的浓度范围与醇溶液出现边界不稳定性碎裂为小液滴的浓度范围一致,后续用实验验证了计算得到的发生“马兰戈尼爆裂”的浓度区间的准确性.

为了使扰动下液柱的流动方程可解,本文采用关于中心轴对称的同心圆柱壳模型简化计算.基于中间层厚度非常薄的假设,对方程进行近似降阶求解得到Plateau-Rayleigh 不稳定性不同模式的扰动增长率,并且对于扰动增长率的不同模式做出竞争猜想,得到了扰动增长率的范围.基于猜想和Mathematica 计算分析预测了不同黏度比的液体层和液滴发生“马兰戈尼爆裂”的位置区间,其中醇溶液在花生油表面碎裂为小液滴的位置区间在4.51—5.98 倍液柱宽度,并且通过实验验证预测是准确的.

2 母液滴的铺展过程

2.1 母液滴铺展的浓度

两种由不互溶或部分互溶液体相互接触而形成的界面称为液液界面[26].下文对二元混合物A(如水-醇混合物)在疏水性液体B(如植物油)表面上时形成液液界面的条件进行分析.

设液-液接触面积为单位面积,则在恒温恒压下有

式中,γA,γB和γAB分别为单位面积下A,B 和AB 的界面自由能.ΔG表示吉布斯自由能变,吉布斯自由能的变化可作为恒温、恒压过程自发与平衡的判据.当铺展系数S＞0 时,液体A 才能在液体B 实现铺展.由于界面张力、表面张力与界面自由能、表面自由能在数值上相等;界面张力与表面张力的单位为N/m,界面自由能的单位为J/m2,由J=N·m 可得J/m2=N/m.因此,(1)式也可以表示为

式中σA,σB和σAB分别表示为液体A、液体B 的表面张力和液体A 与液体B 的界面张力.衡量液液界面张力与A,B 两液体表面张力关系,由Good Girifalco 理论[27]推得:

联立(2)式和(3)式可得

根据(4)式和液体A 在液体B 表面实现铺展的条件S＞0,得到二元混合物在液体层表面铺展的表面张力关系式为

可溶性短链醇溶液的浓度和表面张力之间的关系用希斯科夫斯基公式[28]来表示:

其中,σ0和σ分别表示溶剂和醇溶液的表面张力,醇溶液表面张力σA为液体A 的表面张力,K与b均为拟合系数,C为溶液的摩尔浓度.根据(5)式与(6)式推导可得,短链醇溶液发生铺展的浓度关系式为

2.2 母液滴的马兰戈尼流动

当母液滴(醇)溶液浓度达到一定范围时可以铺展形成薄膜.薄膜边缘处的液膜薄、表面积大,挥发速率快,醇浓度远小于中心区域.由(6)式可知,链醇溶液浓度越大,表面张力越小,母液中心与边缘形成表面张力梯度,液体从表面张力低的中心区域向表面张力高的四周流动,形成溶质马兰戈尼流[29],让母液滴在液体层上进一步铺展成厚度更薄的均匀薄膜.

Keiser 等[21]通过量纲分析给出了马兰戈尼爆裂现象的特征半径R*与特征时间T*的表达式,根据v=R*/T*可以推导出马兰戈尼流诱导的流速v与相关参数的关系式:

定义有效张力σ=σmo+σma.σmo为油层与醇溶液的界面张力,σma为醇溶液与空气的界面张力.记中心处溶液体积浓度为ϕ0,有效张力为σm;边缘处溶液体积浓度为ϕc,有效张力为σc,则有Δσ=σm-σc.H为油层厚度,η0为油层的运动黏度.jv为醇溶液的蒸发速率,Ω0为滴加液滴的体积.

当S＜0 时,醇溶液不可以在油层表面发生铺展,铺展的临界体积浓度满足:S(ϕc)=0.即母液滴边缘浓度达到ϕc时,S=0,醇溶液不再润湿油层,达到最大的扩散边界.此时,油的黏性应力与界面张力相平衡,即η0v/H=Δσ/R.再结合(8)式可以得到实现最大铺展的母液半径R:

3 母液滴的不稳定性

3.1 母液滴边缘的不稳定性

当母液滴达到最大母液半径时,可以近似视为一个厚度均匀的圆形薄膜[21].虽然液滴边界处的界面张力已经达到平衡,但是由于最初的蒸发速率差异,液滴内部依旧有浓度差异[30,31],马兰戈尼效应依旧存在[21],液滴内部的流动并未停止[31],又因为Fay[4],Huh 等[5],Foda 和Cox[6]的工作已经证明,若液滴完全处于静止状态下,液滴边缘不会出现不稳定性,液滴铺展成液膜后保持完整,不会发生碎裂,所以推测内部流动未停止可能是引起液滴边界不稳定性的原因.引起扰动的因素很多,机制复杂,但其成因不影响对后续扰动引起的不稳定性增长进行分析.

母液滴扩散到最大母液半径时,扩散过程流动缓慢且流动的母液滴质量很小,属于黏性流动,整个速度场最初是无旋的,并且水和酒精的混合液黏度很小,整个液滴在之后的演化过程中会保持无旋[32].因此,速度势ϕj可表示为∇ϕj=v.由整个液滴的体积一定,整个流场是无源的可得:∇2ϕj=0.如图1 所示,一半径为R0的油层圆形界面,母液滴在其表面铺展,母液滴薄膜厚度为h,且h≪R0.r为液滴边缘某点到液滴中心的距离.在柱坐标下,对于其中的某一层(厚度为δz)可用极坐标描述:

由流体的边界无滑移条件可知r方向上的速度v只是z的函数[33],垂直于z方向且沿r方向的牵引力为,在某一层上单位体积的两个面牵引力差为,µ表示动力黏度.完全铺展时母液滴边缘处,单位体积所受压力p与两端牵引力之差相平衡,即

由上下表面无滑移的边界条件,可得:

将速度在z方向上进行平均:

考虑的是不可压缩流,且流体的流速较小,则∇·=0,即压力p满足杨-拉普拉斯方程[34],压力差Δp可以表示为

马兰戈尼效应带来的不稳定性对液滴边缘产生了扰动,根据傅里叶变换可知任何扰动都可以表示为一个无限的波函数叠加[35].图1 显示了具有波状扰动a的圆形界面,可以将母液边界形状写为

其中,Am表示与无因次波数m相关的振幅因子,f(t)表示波振幅与时间t相关,ϑ表示波函数的相位因子.

设母液滴流量为Q,对于未扰动情形下的位移R(t)可以表示为

t=t0(初始时刻)时,R(t0)=0,解出未扰动情形下速度势:

其中,µb表示醇溶液与油层界面的动力黏度,µj表示醇溶液的动力黏度,µa表示醇溶液与空气界面的动力黏度.

(17)式求得的速度势仅为稳定条件下的.对于不稳定情况下加入扰动项得

式中,α为扰动振幅,由理想流体的连续性条件[36]可得

其中,A表征任一波数下的振幅.

(14)式引入微扰项a,由杨-拉普拉斯方程可得界面处得压力差为

根据(20)式可以定性分析指状液柱产生过程,边界处由于扰动产生的凹凸后,凹陷处产生了负曲率导致压差增大,凸起处产生正曲率导致压差减小,凸起部分被两侧凹陷处高压差部分挤压,随着不稳定性液膜不稳定性增长凹凸程度增大,曲率变化明显,压差增大,最终凸起部分被挤出去形成指状液柱,为了衔接后续分析,之后采用扰动波长进行分析.

由于µb≫µj,µj≫µa,联立(13)式、(17)式和(20)式可得

每个m对应一种波长不同的表面振动模式.当=0 时,对应最小波长λc,以保持扰动.根据(21)式解得此时的最小波数mc为

根据mcλc=2πR与(22)式,可推得对应发生失稳的临界波长λc为

并且联立(8)式和(9)式,可得

当母液周长小于临界波长时,位移是稳定的,界面仍然是以滴入点为中心的一个圆.一旦周长大于临界波长,界面就会失稳形成类似手指形状的边缘结构[38].对于醇溶液滴加在油层表面的情况,醇溶液可以在油层表面实现铺展,即满足S(ϕc)＞0,由于马兰戈尼流的作用,母液滴的周长一定大于临界波长.所以只要醇溶液可以在油层表面铺展,边缘就会失稳生长出指状液柱(见图2(a)).

图2 指状液柱碎裂过程的实验图像Fig.2.Experimental images of finger shaped liquid column fragmentation process.

3.2 小液柱碎裂的分析

由图2(b),(c)可知,液膜边缘凹凸生长出的指状液柱,达到一定长度后断裂成小液滴.根据Plateau 的界面自由能理论[39]: 小液柱的长度超过其截面周长时,必然会出现Plateau-Rayleigh 不稳定现象,从而导致了扰动的增长,而表面张力的作用会使液体以最小的表面积形式存在,即碎裂为球状液滴.因此,对液柱的碎裂条件以及碎裂的具体位置展开了分析.

如果直接建立在油层-空气界面上流动的液柱模型,上下表面不对称边界会导致求解液柱的流动方程十分困难,因此建立如图3 所示的同心圆柱壳模型.在同心圆柱壳模型下当R(2)=R(1)(1+ε)(ε→0)时,中间层的厚度与曲率半径相比很小,近似看作平面,圆柱形薄壳在两个同心圆柱之间的流动近似看作是液柱在两界面之间流动[40]且该模型是关于中心轴对称的.µ(n) 表示第n层流体的动力黏度,γ(n) 表示第n层界面张力系数.

图3 同心圆柱壳模型示意图Fig.3.Schematic diagram of a concentric cylindrical shell model.

对于因为Plateau-Rayleigh 不稳定性而扰动的界面,可以定义一个界面函数:

其中,k表示扰动的波数,ω为扰动的频率.

根据Liang 等[41]提出的模型,在Plateau-Rayleigh 不稳定情况下液柱的流动方程可表示为

这里,A(n,n) 和B(n) 为4×4 矩阵:

R(2)=R(1)(1+ε)(ε→0)时,ε是小量,将det(M(n))=0 以ε的级数展开可解得扰动的色散关系ωj(k)(j∈(1,N-1),N=3),此时扰动的增长率σj(k)=Imωj(k)有两个解:

由于上下两层液体与中间液体界面上扰动的相位差,ωj(k) 有两个解,对应扰动增长率有两种模式,分别如图4 所示.σ+(k) 模式对应的是上下两界面的相位差为零,σ-(k) 模式对应的是上下两界面的相位差为 π.ε→0 时,中间层液体非常薄,上下界面基本重合.对于σ+(k)=σ0(k)+O(ε),由于两界面扰动相位差为零,扰动模式一致,可以认为上下界面是同一个界面,三层结构就变成了双层结构,但是上层液体并不是单一的n=3 层流体,而是其相关系数由n=2 和n=3 两层液体的耦合决定[41,42].因为n=3 层是空气且基本处于静态,可忽略不计[24],所以σ+(k) 是由里面两层液体形成的双层结构决定的,类似于忽略了中间薄层的存在.对于双层结构的增长率,Tomotika 证明主要与两液体黏度比有关[25],σ0(k) 可表示为

图4 振动模式示意图 (a) σ+(k) 模式;(b) σ-(k) 模式Fig.4.Schematic diagram of vibration mode: (a) σ+(k)mode;(b) σ-(k) mode.

其中ψ(kr) 的具体形式在补充材料B (online)中给出.Tomotika 的实验数据与理论计算结果相比偏大了11%[43],推测这个误差主要来源于O(ε),因为一阶小量不能完全忽略不计.

对Tomotika 的计算结果乘以修正系数1.11,利用Mathematica 对(35)式进行求解,最终得到σ+(k)模式下增长率与波数和黏度比的关系,见图5(a),且借助Mathematica 可以得到黏度比和最大增长率所对应的波数的关系,见图5(b).由图5(a)可知,随着黏度比的减小,增长率呈上升趋势,由图5(b)可知当黏度的取值在0.2208 左右时,最大增长率对应的波数最大.

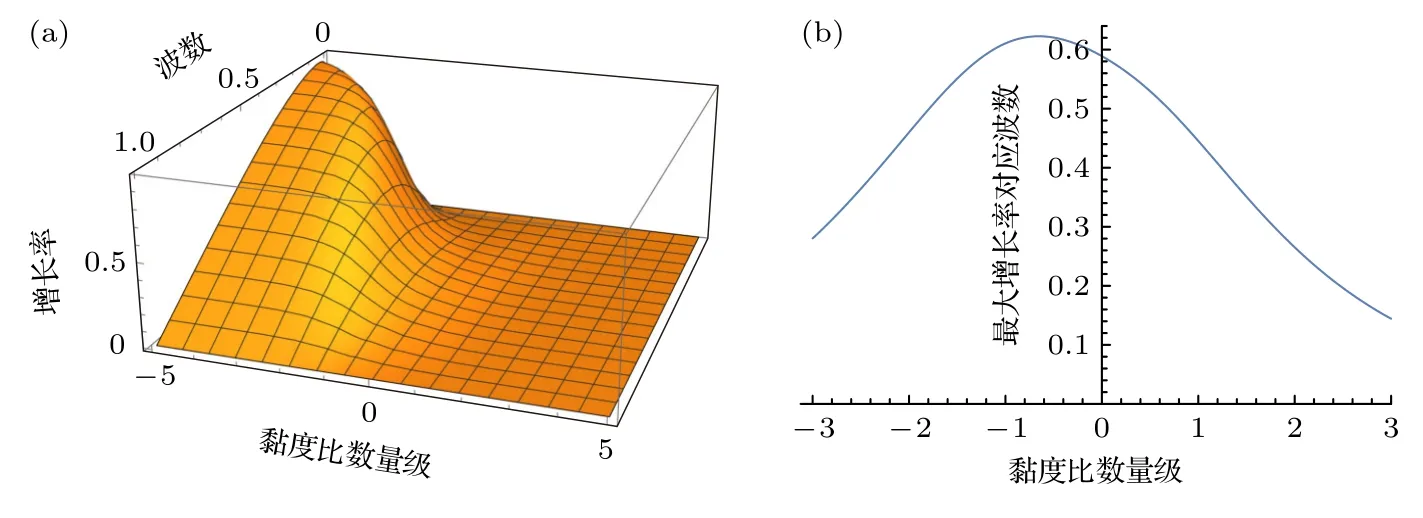
图5 (a) σ+(k) 模式下增长率与波数和黏度比的关系;(b) 黏度比和最大增长率所对应的波数的关系Fig.5.(a) Relation of growth rate to wavenumber and viscosity ratio at σ+(k) mode;(b) relationship between the viscosity ratio and the wave number corresponding to the maximum growth rate.

对于σ-(k) 模式,在ε→0,两界面基本重合时,由于上下两界面的相位差为 π,两种扰动相互抵消,液柱流动可以看作是真空中的液柱流动.从数学角度分析,σ-(k)=O(ε2) 在ε→0 的情况下,O(ε2)作为二阶小量可以忽略不记,即两侧液体的影响可以忽略不计.Chauhan 等[44]从物理过程分析也得出了相同的结果.真空中液柱的扰动增长率与波数k的关系由Rayleigh[45,46]于1879 年求出:

对(36)式进行求解,得到σ-(k) 模式下增长率与波数的关系如图6 所示.由图6 可知,最大增长率对应的波数为0.697.液柱最终断裂的位置与液柱宽度的比例已被证明只与最大增长率σmax对应的波数相关[47],当以最大增长速率增长到一个波长时液柱就会发生碎裂[39],所以碎裂长度与最大增长率所对应波长相等.

图6 σ-(k) 模式下增长率与波数的关系Fig.6.Relation of growth rate to wavenumber and viscosity ratio at σ-(k) mode.

不同于一层液柱或两层液柱σj(k) 的解是唯一的,在N=3 时σj(k) 有两个解:σ+(k),σ-(k),分别对应上下两个界面扰动的相位差为0 和 π;在两种模式最大增长率对应的波数相差较大的情况下,液柱生长的过程中会选择最大增长率对应波数较大即波长较短的模式,这种情况已被广泛验证[41].但在本问题中,σ+(k) 最大增长率对应波数由醇溶液与花生油的黏度比代入(35)式解得:kr=0.506;σ-(k)最大增长率对应波数由(36)式可知:kr=0.697,两种模式最大增长率对应的波数相差较小情况下,两种模式可能处于竞争状态,上下界面扰动的相位差随机介于0 到 π 之间,液柱真实的断裂位置也是介于σ+(k),σ-(k) 模式最大增长率分别对应断裂位置之间的一个区间.根据图5(b)可知σ+(k)模式下黏度比和最大增长率对应波数的关系,又由σ-(k) 模式最大增长率对应的波数为0.697,可以得到在σ+(k),σ-(k) 模式最大增长率对应的波数的区间,如图7 所示.

图7 不同黏度比下两种模式最大增长率对应的波数的区间Fig.7.Interval of the wavenumber corresponding to the maximum growth rate of the two modes at different viscosity ratios.

图7 中红线表示在σ-(k) 模式下最大增长率对应的波数,蓝线表示σ+(k) 模式下黏度比和最大增长率对应波数的关系.在波数相差较小时,可以根据两种模式最大增长率对应的波数的区间得到液柱碎裂位置区间.

4 实验系统及测量结果

实验分别验证了前两节理论分析结果的正确性,对发生马兰戈尼爆裂时醇溶液的浓度范围和液柱碎裂位置进行了计算与测量.用0.04 mol/L 的亚甲基蓝为醇溶液染色,配制不同浓度的醇溶液,在25 ℃的恒温槽中进行实验.用最大气泡压力法[48]测定了25 ℃下油的表面张力系数(见表2).利用光杠杆法测量油层厚度并控制每组实验时油层厚度为4 mm,用竖直针管滴加醇溶液来保证液滴稳定竖直滴落,其中注射泵每次滴加醇溶液的体积为1 μL.由于乙醇的安全性较高,改变液体层B 的种类进行实验时,使用乙醇溶液为二元混合物.使用相机俯拍录制实验视频,记录发生马兰戈尼爆裂的实验现象.

4.1 醇溶液浓度范围的计算与实验测量

将文献[26]中25 ℃下几种醇溶液的表面张力与浓度关系的实验数据进行拟合[49],得到K与b的值(见表1).油的表面张力系数σB,25 ℃下水的表面张力系数σ0(0.072 N/m)与K,b值代入(7)式可得醇溶液发生马兰戈尼爆裂的理论摩尔浓度范围(见表1 和表2).

表1 不同醇溶液发生爆裂现象的理论浓度范围与实验浓度范围Table 1.Theoretical concentration range and experimental concentration range of burst phenomena in several alcohol solutions.

表2 花生油,蓖麻油为液体B 时,乙醇溶液发生爆裂现象的理论浓度范围与实验浓度范围Table 2.Theoretical concentration range and experimental concentration range of ethanol solution when peanut oil and castor oil are liquid layers B.

根据实验现象记录4 种醇溶液在花生油表面发生马兰戈尼爆裂的体积浓度范围(图8)以及乙醇溶液在花生油和蓖麻油层上发生马兰戈尼爆裂的体积浓度范围(图9).由图表可知,各组实验的数据点均在理论计算值范围内,实验测量的醇浓度范围的下限略大于理论计算值,考虑与滴加醇溶液时醇已少许挥发致使滴加的实际溶液浓度偏小有关.Keiser 等[21]通过干涉仪测量得到了异丙醇溶液发生马兰戈尼爆裂的体积浓度范围(≥35%±2%),该实验值与本文理论值相符.

图9 花生油,蓖麻油为液体B 时,乙醇溶液是否发生爆裂现象的体积分数统计数据Fig.9.Statistical data of volume fraction of ethanol solution with peanut oil and castor oil as liquid B.

4.2 醇溶液在油层表面液柱碎裂区间长度的计算与测量

由于液柱碎裂的长度与波长相等,由l=λ=2π/k,将醇溶液与花生油的黏度比1/45 代入(35)式,利用Mathematica 对代入黏度比后的(35)式求最大值位置可得,σ+(k) 模式最大增长率对应的kr=0.509,将kr=0.509 代入l=λ=2π/k可得l=5.89d.同样的方法可以得到,σ-(k) 模式最大增长率对应的kr=0.697,代入l=λ=2π/k可得l=4.51d.

将异丙醇溶液在花生油表面发生马兰戈尼爆裂的视频导入软件Tracker 中进行测量.均匀选取液滴边缘的40 个不同位置,分别测量前后三次断裂液柱的宽度d与断裂位置的长度L,各个位置L/d的比值如图10 所示.

图10 液柱碎裂位置L/d 数据点Fig.10.Liquid column fragmentation location L/d data point.

5 结果与讨论

本文从“马兰戈尼爆裂”过程可以分为“润湿铺展”和“失稳碎裂”两个阶段的基础思想出发,基于Hernández-Sánchez 等[23]实验结果和Huh 等[5]、Foda 和Cox[6]理论研究的悖论、小液柱的不对称边界等问题,提出猜想和假设并且完整解释了“马兰戈尼爆裂”现象的物理机制,并通过实验验证发现实验结果与理论预测相符.工作的重点部分有以下几点.

本文得出了二元混合物在液体层上发生铺展的判定通式.基于通式代入二元混合物表面张力与浓度的关系式便可以推得二元混合物在液体层上发生铺展的浓度范围可以为实际应用生产提供一定的理论指导.如在半导体成膜工艺中利用马兰戈尼流[50]构筑成膜溶液: 按比例混合具有高沸点、低表面张力的甲苯与具有低沸点、高表面张力的四氯化碳两种溶剂,在成膜溶液中形成马兰戈尼流,可有效降低“咖啡环”效应[51],提高薄膜均匀性.但当生长薄膜的溶液浓度较低时,薄膜无法覆盖完全;浓度超过一定值时,薄膜趋向于无序生长.依据(5)式可以得到准确的成膜溶液的浓度范围,为实际应用生产提供理论指导.

液滴内部浓度差异引起马兰戈尼效应导致了液滴边界失稳,基于此本文求解出了边界失稳的临界波长和生长液柱的特征波长.对于醇溶液滴加在油层表面的情况,只要醇溶液可以在油层表面实现铺展,对应的扰动波长一定大于临界波长,边缘就会失稳生长出指状液柱,液柱生长到长度大于液柱截面周长时便会发生碎裂.醇溶液在油层表面铺展的浓度范围与发生马兰戈尼爆裂的浓度范围一致,实验验证醇溶液在油层表面发生马兰戈尼爆裂浓度范围与预测范围一致,理论与实验结果高度吻合证明了对铺展的判定通式推导和对边界失稳的原因解释的正确性.同时,还发现如果使用单参数短链醇表面张力与浓度的关联式进行拟合,此时正丁醇发生马兰戈尼爆裂的浓度不存在上限[31],与真实实验不符.所以使用单参数关联式拟合表面张力与浓度的关系并不一定适用于所有短链醇.这证明铺展的判定通式在表面张力与浓度的参数拟合中可能具有更广泛的用途.此外,本文推导的临界波长与最大波长的结果与Hele-Shaw 流黏性指进模型结果类似[20],不同的是驱动Hele-Shaw 流的压力差为两板之间的压力,而驱动母液滴边缘生长出指状液柱的压力差为界面张力梯度.虽然压力差来源不同,最终解的形式相似,这也印证了(23)式和(24)式即临界波长与最大波长是正确的.

为了解释液柱碎裂的原因和具体位置,引入了同心圆柱壳液柱微扰模型.在R(2)=R(1)(1+ε)(ε→0)即中间层非常薄的情况下,液柱的流动方程可解.并且对于多解情况下液柱不稳定性的实际增长率,依据扰动相位差的分析,对两种模式最大增长率对应的波数相差较小情况做出了解释和预测.在异丙醇溶液在花生油表面扩散的实验中测量了40 个位置连续三次碎裂时液柱的长度与宽度的比值,120 个数据全部在预测的4.51—5.98 倍的液柱宽度区间内.当然虽然实验结果在预测的区间内,但并没有集中在某个特定的值附近,而是随机地分布在预测的区间当中,后续研究会进一步讨论竞争模式更加精确的机制.特别地,3.2 节提出的简化模型有可能为界面处的Plateau-Rayleigh 不稳定性分析提供新的思路.不对称边界导致方程过于复杂的问题普遍存在,例如2008 年Eggers 和Villermaux[20]创举性地实验证明了在Plateau-Rayleigh 不稳定下碎裂形成的小液滴直径只与不稳定性最大增长率成正比后,基于Plateau-Rayleigh不稳定生成微液滴和制备纳米颗粒的方法被广泛研究和应用[52],并且在化工微量反应和纳米颗粒制备等研究领域成为一种新兴的研究热点.因为界面处不对称边界条件的复杂性,之前的研究都是有关液柱包埋在其他液体中生成微液滴的.微液滴或者颗粒都是在包埋液体中生成的,那么当微液滴或者颗粒的尺寸达到纳米量级时,如何将生成物从包埋液体中提取出来就成了一大技术难题,而3.2 节的简化模型有可能让生成微液滴的过程在液体层表面进行,这将极大地简化生成物提取问题,解决这一技术难题.

6 总结

本文解释了马兰戈尼爆裂现象的物理机制.本研究中被实验初步验证的猜想、假设以及简化模型,可能为成膜技术、涂层工艺等已有的应用领域提供一定的理论指导,为化工领域微量反应和纳米颗粒制备等研究领域中的一些技术难题提供新的解决思路.也有一些问题需要更进一步的研究,例如对高雷诺数流体不稳定性的讨论和在不稳定多解情况下竞争模式更加精确机制的研究,后续工作也将以研究Plateau-Rayleigh 不稳定性更广泛更精确的机制为目标展开.