泵控液压垫预加速阶段最优控制策略

何 松,董志奎,安会江,王 翟,张勇斌

(1.燕山大学 机械工程学院,河北 秦皇岛 066004; 2.北自(北京)检测科技发展有限公司,北京 100032)

引言

电液伺服泵控液压拉伸垫(泵控液压垫)是衬托在模具下方,用于增加拉伸阻尼以保证材料均匀流动的冲压设备。随着航空航天以及汽车领域的迅速发展,拉伸成型产品对液压垫系统在制造工艺和可靠性上提出了更高的要求[1-2]。传统阀控液压垫系统的构型设计和控制策略已经发展较为成熟[3],但是其存在能量利用率不高、系统组成复杂等缺点[4],因此采用结构紧凑、能量利用率高的泵控系统替代阀控系统构成新型泵控液压垫[5-7],将有助于提高液压垫的产品竞争力。

目前泵控系统的速度、位置、压力等单一控制策略得到了迅速的发展,并且针对不同的工况形成了更加完备的解决方案[8-9]。然而,泵控液压垫预加速阶段对响应速度和精度要求较高,需要将单一的速度控制策略和位置控制策略相结合,探索高效可靠的速度位置复合控制策略。针对速度位置复合控制策略,国内外学者进行了大量研究。何建海等[10]针对风帆液压控制过程中液压冲击对风帆系统的影响,提出了油缸速度前馈和风帆转角位移综合协调控制方案,减小了风帆控制过程中的速度冲击。ZHANG Xiaogang等[11]针对挖掘机在危险环境中对位置控制和速度控制的高精度问题,提出一种结合速度前馈的位置控制策略,使挖掘机臂同时实现位置和速度控制,保证了挖掘机臂的平稳移动和快速定位。HUANG Weinan等[12]针对传统大型惯性液压回转系统生产效率低、重复定位精度差等问题,提出了一种基于独立计量控制系统的速度位置复合控制策略,提高了系统的动态特性及生产效率。乔志刚等[13]针对快锻液压机的控制精度与响应速度问题,提出快锻液压机速度位置复合控制策略,使锻压机的活动横梁能够无滞后地实现高精度定位。上述研究为泵控液压垫最优控制策略研究奠定了良好的基础。

本研究针对泵控液压垫预加速阶段的工艺要求,从速度位置复合控制策略出发,提出了一种基于S型曲线规划的泵控液压垫预加速阶段最优控制策略,使得泵控液压垫在满足工艺要求的前提下,降低工作过程中的冲击和振动,提高拉伸成型产品的质量并延长设备的使用寿命。

1 系统组成

泵控液压垫系统原理如图1所示,包括伺服电机、定量柱塞泵、蓄能器、单向阀、溢流阀、液压缸等元件组成。其中,柱塞泵输出的流量取决于伺服驱动器控制伺服电机的转速,流量传递至液压缸,进而实现液压垫的速度、位置控制。

1.伺服电机 2.定量柱塞泵 3.单向阀 4.溢流阀 5.对称液压缸 6.负载 7.蓄能器

泵控液压垫伺服控制系统主要包括电气控制系统、伺服驱动系统、液压执行系统。

电气控制系统又分为上位机数据采集系统和伺服控制系统,可对采样数据实时监控与处理。伺服驱动系统包含伺服驱动器和永磁同步交流伺服电机。液压执行系统则由定量柱塞泵、对称液压缸等元件组成。泵控液压垫控制系统组成如图2所示。

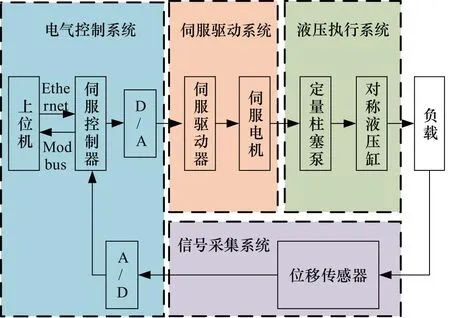
图2 泵控液压垫伺服控制系统组成

2 系统建模

2.1 伺服电机模型

为了简化建立伺服电机数学模型的难度,通常忽略其铁芯饱和、铁耗、转子阻尼等对伺服运动的影响,在d-q坐标系下建立伺服电机的数学模型。

伺服电机的转矩方程:

(1)

式中,Tm——电磁转矩

pn——转子磁极对数

ψf——永磁体在定子绕组上产生的磁链

i——定子电流

Kt——电磁转矩系数

(2)

式中,E0——空载状态下伺服电机的反电动势

f——交流电频率

ω——伺服电机角速度

r——同步电机转速

伺服电机拖动系统的运动方程:

(3)

式中,Jm——折算到电机轴上的转动惯量

Bm——摩擦阻尼

TE——负载力矩

在伺服电机等效电枢回路中,根据基尔霍夫电压定律,得出电压平衡方程:

(4)

式中,Us——定子电压

Ke——反电动势系数

Ls——定子电感

R——定子电阻

2.2 定量柱塞泵模型

由于定量柱塞泵在工作状态下,存在内泄漏和外泄漏的现象,故建立数学模型时需要考虑此因素的影响,泵正向运转时流量和压力关系如图3所示。

图3 定量柱塞泵流量与压力关系图

定量柱塞泵1口流量方程:

Q1=nDp-Qil-Qel1

(5)

定量柱塞泵2口流量方程:

Q2=nDp-Qil+Qel2

(6)

式中,Dp——柱塞泵排量

n——柱塞泵转速

Qel1——柱塞泵1口处外泄漏流量

Qel2——柱塞泵2口处外泄漏流量

Qil——柱塞泵内泄漏流量

2.3 液压缸模型

液压缸作为泵控液压垫系统的执行元件,其结构如图4所示,建立液压缸的流量连续性方程如下所示。

图4 液压缸结构

流量连续性方程:

(7)

(8)

式中,QA——液压缸左腔流量

QB——液压缸右腔流量

Cip——液压缸内泄漏系数

Cep——液压缸外泄漏系数

p1——液压缸左腔压力

p2——液压缸右腔压力

V10——回油腔的初始容积

V20——进油腔的初始容积

βe——有效体积弹性模量

3 复合控制策略

本研究将从位置控制和速度控制策略出发,对泵控液压垫预加速阶段的速度位置复合控制策略进行研究,提出基于曲线规划的速度位置复合控制原理。首先,采用S型加减速曲线规划方法对泵控液压垫的速度曲线进行规划;其次,基于泵控液压垫系统状态空间模型,设计速度状态观测器;最后,结合最优控制思想,设计速度位置切换最优控制策略,来完成泵控液压垫的预加速控制算法研究。

3.1 S型加减速曲线规划

泵控液压垫预加速阶段要求位置动态跟随的快速性和准确性较高,因此选用7段S型曲线中的前4段,降低系统在预加速阶段的冲击和振动。S型加减速曲线相比于传统的曲线规划方法,可使此系统在开始阶段和结束阶段均为平滑过渡,并且运行过程中不存在加速度跃变现象[14-16],其加减速曲线规划如图5所示。

图5 S型加速减速曲线速度与时间的关系

3.2 速度状态观测器

为了对控制系统实现状态反馈,根据系统的输入变量和输出变量的实测值得出状态变量估计值的动态系统,称为状态观测器。

本研究采用龙伯格状态观测器,其主要包含观测器模拟部分和修正部分:

(9)

式中,A——状态矩阵

B——输入矩阵

C——输出矩阵

L——观测器增益矩阵

图6 速度状态观测器

3.3 最优控制策略

由于系统对速度、位置均有精度要求,故根据泵控液压垫的速度位置复合控制构建最优控制二次型函数:

J=XTQdrdX+XTRruX+XTQvrvX

(10)

式中,Qd——位置控制模式权重矩阵

Qv——速度控制模式权重矩阵

R——能量输入权重矩阵

rd——位置控制权重系数

ru——能量输入权重系数

rv——速度控制权重系数

最优控制策略通过对位置控制权重系数rd和速度控制权重系数rv的切换,可实现泵控液压垫预加速阶段速度位置的平稳切换。本研究选取液压缸的运行速度作为切换条件,当运行速度小于速度设定值时,为位置控制模式;运行速度等于速度设定值时,位置控制模式无冲击地切换至速度控制模式。

权重系数切换方程:

(11)

基于S型曲线规划的最优控制如图7所示。

图7 基于S型曲线规划的最优控制

4 试验验证

为进一步验证最优控制策略的可靠性,搭建泵控液压垫模拟试验台如图8所示,试验台通过电气控制系统对液压伺服部分实现闭环控制,采用上位PC机与伺服控制器进行实时数据通讯,完成对泵控液压垫速度和位置的监控及存储。

图8 泵控液压垫模拟试验台

基于泵控液压垫模拟试验台,对S型曲线规划的最优控制策略和PID控制效果进行对比验证。设定泵控液压垫运行速度9 mm/s,加速度15 mm/s2,加加速度1 mm/s3,在该工况下进行试验验证,泵控液压垫试验主要参数如表1所示。试验结果如图9、图10所示。

表1 液压垫主要参数

图10 给定速度9 mm/s,加速度15 mm/s2时的实验速度

观察图9b位移误差ey对比曲线和图10b速度误差ev对比曲线,泵控液压垫模拟试验台从1 s起开始动作,系统在整个起步阶段会出现位移突变和速度突变的现象。该现象产生的原因是泵控液压垫试验台需要突然加速,克服静摩擦力和黏性阻尼力,导致液压缸会产生一定的压力。系统的长软管在低压力下内壁弹性模量具有较严重的非线性,因此导致起动时系统压力突变,进而产生速度和位移突变。然而,当泵控液压垫在预加速阶段开始时,上模和下模尚未接触,在1～1.5 s的突变现象不会对整个系统的控制产生影响。系统在2 s以后逐渐趋于平稳,能够满足控制要求。

由图9可以看出,最优控制与PID控制相比,最优控制的位置控制效果较好。最优控制位移响应曲线与理论位移曲线基本重合,2 s以后稳态位置偏差控制在0.02 mm以内。PID控制误差波动较大,最高达0.5 mm,且难以达到稳定状态,不能满足高精度的控制要求。

由图10可以看出,最优控制的实际运行速度接近理论速度,2 s后达到速度设定值9 mm/s。最优控制稳态速度偏差在0.17 mm/s以内,控制效果较好。PID控制速度偏差在0.7 mm/s以内,难以满足高精度的控制要求。

虽然在实际实验过程中,泵控液压垫模拟试验台容易受到外部干扰等因素的影响,但是最优控制策略的控制效果在误差允许的范围内满足预加速阶段的工艺要求。

5 结论

通过对液压垫系统进行分析得出预加速控制的关键在于液压垫预加速过程中的速度和位置控制。针对泵控液压垫预加速阶段控制方法展开研究,通过理论研究和试验分析,主要得到以下结论:

(1) 针对泵控液压垫系统,提出了S型加减速曲线规划方法,使其在预加速阶段运行过程中不存在加速度跃变现象;

(2) 对泵控液压垫预加速阶段的速度、位置控制进行研究,提出了基于S型曲线规划的最优控制策略;

(3) 对泵控液压垫系统预加速阶段的最优控制策略进行了理论和试验研究。结果表明,最优控制策略相比于传统的PID控制具有良好的控制效果,且满足泵控液压垫的工艺需求。