基于自适应阻抗控制的大负载液压机械臂柔顺控制
陈少南,赵桂生,刘 蕾,陈国栋
(中广核研究院有限公司,广东 深圳 518026)
引言
近年来,随着重载机械臂操作灵活性和准确性的提高,重载机械臂在工业领域的应用越来越丰富,代替人完成了各种超出人类能力范围的特种工作[1-3]。大负载液压机械臂凭借其在复杂环境下的高负载作业能力,越来越多的应用在各种特种作业领域[4-5]。然而,目前液压机械臂末端的作业属具与作业对象大多是刚性接触。当作业属具与精密零件作业对象产生接触时,如果机械臂不能具备一定的柔顺性,将会对精密零件作业对象产生较大的振动冲击,甚至有可能损坏作业对象,影响机械臂的作业能力[6-7]。因此,实现液压机械臂的柔顺控制是亟需解决的问题。
针对机械臂的柔顺控制问题,国内外学者开展了相关研究。MASON M T[8]提出了力位混合控制思想,将机械臂的运动空间分解为力自由空间和位置自由空间两个正交子空间,对力与位置进行独立控制,实现机械臂柔顺控制。HOGAN N[9]提出了阻抗控制思想,通过调整期望阻抗模型中的惯性、阻尼和刚度矩阵,可以改变机械臂阻抗特性达到调整机器人与环境交互力的作用,实现机械臂的柔顺控制。LEE K[10]提出了一种力跟踪阻抗控制算法,在未知环境下通过在线改变阻抗控制的刚度参数以调节环境接触力,并进行了算法的稳定性分析。
针对上述情况,本研究以大负载液压机械臂为研究对象,进行了机械臂柔顺控制研究。在基于位置的阻抗控制算法基础上,提出一种通过环境参数估计来生成参考轨迹的自适应阻抗控制算法用于大负载液压机械臂的柔顺控制,开展大负载液压机械臂管道搬运实验,进行自适应阻抗控制算法性能验证。
1 液压机械臂液压系统分析
本研究的研究对象为双液压机械臂,主机械臂为五自由度机械臂,副机械臂为六自由度机械臂。以主机械臂为例,分析液压系统组成。主机械臂主要包括第一臂、第二臂、第三臂、摇臂、摆臂、各臂驱动油缸、快换系统和作业属具等,如图1所示。

图1 机械臂系统示意图
各臂驱动油缸液压系统如图2所示,主要由位移传感器1、负载2、电液比例换向阀3、溢流阀4、液压泵5、放大器6、液压缸7、数据采集卡和工控机组成。系统工作时,位移传感器1将液压缸7当前的活塞杆位置信号,通过A/D转换后在CPU中计算偏差值,将控制量经过D/A转换和放大器6放大后控制电液比例阀3开口大小,从而控制液压缸7中活塞杆位置,使各机械臂关节运动到期望位置。
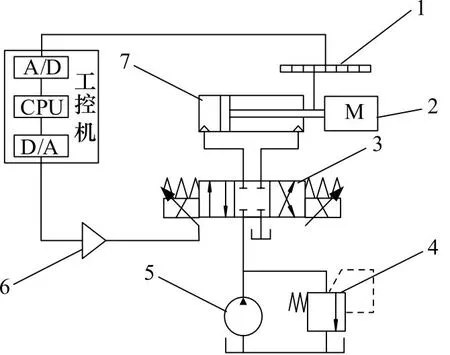
图2 液压系统原理图
2 基于位置的阻抗控制
阻抗控制方法可以分为基于力矩的阻抗控制和基于位置的阻抗控制,两种阻抗控制方法均通过期望阻抗关系实现机械臂力和位置的动态关系调整。其区别在于,基于位置的阻抗控制是根据反馈的接触力信息调节位置以进行位置控制,基于力矩的阻抗控制是根据反馈的位置信息调节力矩以进行力矩控制。基于力矩的阻抗控制方法需要机械臂开放力矩控制的接口,且需要预知机械臂的精确动力学模型,而多自由度机械臂的动力学模型求解往往是比较困难的[11-13]。因此,在实际应用中,大多采用基于位置的阻抗控制进行机械臂的柔顺控制。
当机械臂末端与作业环境接触时,将机械臂末端等效如图3所示的弹簧-质量-阻尼二阶系统阻抗模型,根据机械臂末端与环境的接触力误差修正机械臂末端的参考轨迹,实现机械臂末端与环境保持期望接触力。

图3 弹簧-质量-阻尼二阶系统阻抗模型
机械臂末端与环境作用的阻抗模型可以表示为:
(1)
式中,M——阻抗模型的惯性参数矩阵
B——阻抗模型的阻尼参数矩阵
K——阻抗模型的刚度参数矩阵
Xd——机械臂末端位置期望值
X——机械臂末端位置实际值
Fd,Fe——机械臂末端与环境的期望接触力和实际接触力
基于位置的阻抗控制由位置控制内环和阻抗控制外环组成,其控制框图如图4所示。首先获取机械臂与末端环境的实际接触力Fe,阻抗控制器将实际接触力Fe与期望接触力Fd的误差通过阻抗关系转化为末端位置修正量ΔX,末端期望位置Xd经过末端位置修正量ΔX修正后,由机械臂逆运动学得到机械臂各关节角度,进入位置控制内环,控制关节运动。经过阻抗控制器的期望位置修正后,使机械臂末端力误差减小,进而满足机械臂力位期望动态关系。

图4 基于位置的阻抗控制框图
然而,传统的基于位置的阻抗控制没有考虑到环境特性的影响[14-15]。当机械臂的作业对象发生改变时,机械臂的环境刚度等参数也会发生改变。传统的阻抗控制需要根据不同环境试选不同的阻抗参数,才能够获得相对较好的力控效果。
3 基于参考轨迹生成的自适应阻抗控制
阻抗控制需要把参考轨迹和接触力误差作为输入,设计合适的参考轨迹可以改善阻抗控制的控制性能。然而参考轨迹的设计存在一定困难,如果能够根据测量的接触力来确定参考轨迹,就可以极大地简化控制器的设计。
3.1 参考轨迹设计
阻抗模型在空间6个自由度上是可以解耦的,为简化分析,将阻抗模型解耦到每一维度,则式(1)转化为:
(2)
式中,m,b,k分别为每一维度下的惯性参数、阻尼参数和刚度参数;Δx=x-xd为机械臂末端实际位置与期望位置的偏差;ef=fe-fd为机械臂末端实际接触力与期望接触力的偏差。
传统的基于位置的阻抗控制只考虑了机械臂自身的阻抗特性,并没有考虑到环境参数对控制性能的影响。因此,需要首先对环境建模,分析环境参数对阻抗控制性能的影响。本研究针对的液压机械臂作业对象一般为硬质刚性金属工件,可以只考虑环境刚度,将其简化为一阶线性弹簧模型。根据胡克定律,环境接触力可以表示为:
(3)
式中,ke,xe分别表示某一维度的环境刚度和环境位置。
在式(2)中应用式(3),并假设x>xe,可得:
(4)
由式(4)变换后可以得到系统达到稳态的接触力误差ef计算公式为:
(5)
为使系统稳态时的接触力误差为0,只需设置参考轨迹为:
(6)
但实际上环境位置xe和环境刚度ke难以测量,需要进行环境参数估计。
3.2 环境参数估计
环境位置和环境刚度等环境参数,在各种机械臂作业工况下是不同的。为了使机械臂在不同的作业环境下都能够获得较好的力控性能,需要对环境刚度和位置等参数在线估计[16-17]。采用基于李雅普诺夫理论的参数自适应估计方法,对环境刚度和位置参数进行在线估计,进而设计参考轨迹。
将式(3)中的环境参数替换为估计值,假设x>xe,可得:
(7)



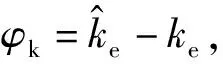
(8)
下面根据李雅普诺夫稳定性理论,对环境刚度和环境位置进行估计。定义Lyapunov函数为:
(9)
其中,α,β均为正常数。
将式(9)对时间微分,可得:
(10)
假设环境位置xe和环境刚度ke为时不变的参数,则有:
(11)
(12)
将式(12)代入式(10)并且化简,得到:
(13)
由式(13)可知系统稳定。式(12)给出了环境刚度和环境位置估计值的微分方程,可以求解得到环境刚度和环境位置估计值如下:
(14)
将式(14)作为环境参数估计方法,以估计环境刚度和环境位置信息。α和β可取值为任意的正常数,不会影响系统的稳定性。在机械臂的阻抗力控过程中,根据力信息和位置信息实时在线估计环境刚度和位置信息,并将环境刚度和位置信息的估计值代入式(6),进行参考轨迹的修正,将修正后的参考轨迹输入至位置控制内环,以实现自适应的阻抗控制,控制原理框图如图5所示。

图5 自适应阻抗控制原理图
3.3 算法仿真
在Webots中,搭建如图6所示的仿真环境。由于阻抗控制算法在每个自由度是解耦的,以z方向为例,对主机械臂分别采用传统阻抗控制算法和自适应阻抗控制算法仿真。

图6 Webots仿真环境
为模拟机械臂实际作业时环境刚度突变的情况,将环境刚度ke设置为:
(15)
设置期望力fd=500 N,环境位置xe=0.5 m,由式(3)计算得到机械臂末端受到的实际力fe。设置环境估计算法参数α=1,β=1。仿真得到的接触力曲线如图7、图8所示。
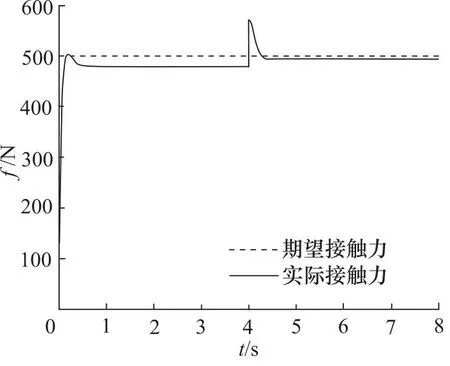
图7 传统阻抗控制算法仿真曲线
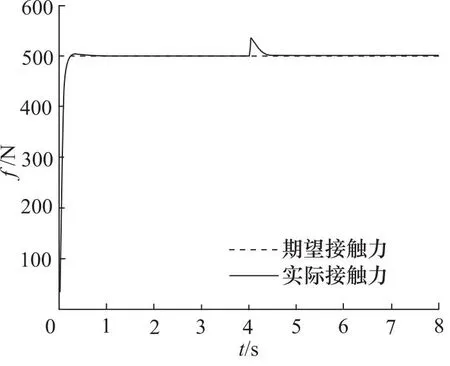
图8 自适应阻抗控制算法仿真曲线
由曲线可以看出,相比于传统阻抗控制算法,自适应阻抗控制算法能够有效地消除系统的稳态误差。当环境刚度发生突变时,自适应阻抗控制算法能够更好地适应环境刚度变化,具有更小的超调量,接触力曲线更加平滑,验证了自适应阻抗控制算法的有效性。
4 液压机械臂管道搬运实验验证
搬运任务是重载机械臂一类典型的工作任务,对于长直管道这种作业对象,适合使用双机械臂进行协同搬运[18-20]。然而,当双臂协同进行载荷搬运时,如果不能对接触力进行柔顺控制,则会容易损坏作业对象。双液压机械臂实验平台管道搬运实验,如图9所示。

图9 双液压机械臂管道搬运实验平台
实验平台主要由履带底盘、回转平台和主副机械臂及其作业属具组成。履带底盘和回转平台在管道搬运实验中保持静止。主机械臂和副机械臂在管道搬运实验中分别采用搬运夹和抓斗作为作业属具。管道质量为200 kg,由双机械臂协同搬运。其中,主机械臂末端安装了六维力传感器实现力信息的获取,在搬运实验中采用阻抗控制方案,用于验证自适应阻抗控制算法,副机械臂全程采用位置控制。机械臂阻抗控制算法编写为C++程序,基于TwinCAT3平台实现机械臂的阻抗控制。
实验任务为双机械臂协同搬运管道,抬升0.5 m后下降。实验过程可分解为以下4个阶段:
(1) 副机械臂抓取管道,主机械臂末端移动到管道附近,等待抓取;
(2) 主机械臂抓取管道;
(3) 主机械臂和副机械臂协同搬运管道并抬升;
(4) 主机械臂和副机械臂协同搬运管道并下降。
首先采用传统的阻抗控制算法进行2次上述实验任务,其中机械臂给定期望接触力分别设置为500 N和1500 N。进行末端作业属具的重力补偿后,记录力传感器z方向的接触力数据,如图10、图11所示。
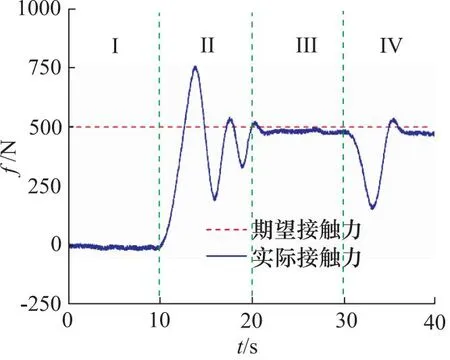
图10 传统阻抗控制算法接触力曲线(500 N)
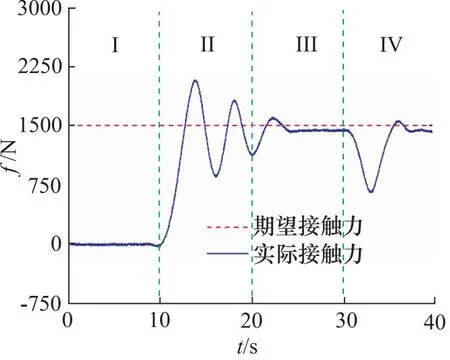
图11 传统阻抗控制算法接触力曲线(1500 N)
由图10和图11中曲线可以看出,第I阶段(0~10 s)主机械臂与管道未产生接触时,末端力传感器只受末端属具的重力,力传感器数据经过主机械臂末端执行器的重力补偿后,数值接近于0;第II阶段(10~20 s)抓取管道过程中,由于接触力的突变,实际接触力产生了一定的振荡,且需要较长时间才能稳定在期望接触力附近;第III阶段(20~30 s)双机械臂同步抬升管道过程中,主机械臂实际接触力能较好的稳定在期望接触力附近;在第IV阶段(30~40 s)同步下降过程开始时,由于机械臂移动方向的改变,接触力产生了一定程度的突变,并在一段时间后重新稳定在期望接触力附近,但存在一定的稳态误差。
然后采用自适应阻抗控制算法进行同样2次实验任务,其中机械臂给定期望接触力同样设置为500 N和1500 N。设置环境估计算法参数α=1,β=1。进行末端作业属具的重力补偿后,记录力传感器z方向的接触力数据,如图12和图13所示。
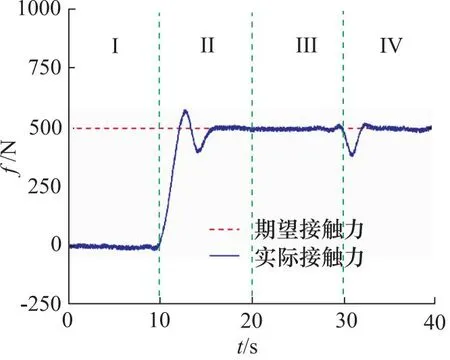
图12 自适应阻抗控制算法接触力曲线(500 N)
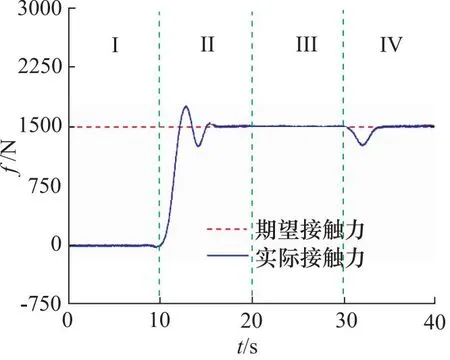
图13 自适应阻抗控制算法接触力曲线(1500 N)
分析两组曲线可知,相比于采用传统的阻抗控制算法,主机械臂采用自适应阻抗控制算法进行实验的接触力稳态误差较小。并且在第II阶段(10~20 s)主机械臂抓取管道和第IV阶段(30~40 s)主机械臂移动方向改变时,接触力的产生的振荡和突变程度较小,且能较快的稳定在期望接触力附近。相比于传统的阻抗控制,自适应阻抗控制算法具有更优的力控性能。
4 结论
本研究以大负载液压机械臂为研究对象,进行了基于自适应阻抗控制算法的机械臂柔顺控制研究。自适应阻抗控制算法通过力和位置信息,进行环境刚度等信息的在线估计,并根据环境信息的估计值进行参考轨迹的设计,以适应不同的作业环境,获得更好的力控性能。开展了重载液压机械臂搬运管道实验,结果表明,相比于采用传统的阻抗控制算法,采用自适应阻抗控制算法进行机械臂的柔顺控制可以获得更好的控制性能。

