中考数学探索性问题答题策略——以江苏省部分地市中考试题为例

⦿ 江苏省仪征市实验中学东区校 王小琪

⦿ 江苏省仪征市月塘中学 雷业红

初中数学课程标准要求教师“引导学生通过实践、思考、探索、交流,获得知识,形成技能,发展思维,学会学习”,探索性题型正是为了适应加强对学生综合能力考查的新形势,在近年来中考数学试题中出现的一种新颖的题型.探索性问题的解答过程本身就是一个探索、发现的过程,这一类问题对培养学生的创造性思维、想象能力、实践能力、探索创新能力有很大的帮助.

1 规律探索型

解答规律探索类问题的策略是:运用化归思想,根据题目的设问方式,采用“提出问题-分析问题-解决问题-深度思考”逐步深入的模式分步解答;要善于从所提供的数字或图形信息中,寻求其内在的共同之处,找到这个存在于特殊之中的共性,也就找到了规律.

例1(2022年江苏省盐城市中考试题第27题)

【发现问题】小明在练习簿的横线上取点O为圆心,相邻横线的间距为半径画圆,然后半径依次增加一个间距画同心圆,描出了同心圆与横线的一些交点,如图1所示,他发现这些点的位置有一定的规律.

图1

【提出问题】小明通过观察,提出猜想:按此步骤继续画圆描点,所描的点都在某二次函数图象上.

【分析问题】小明利用已学知识和经验,以圆心O为原点,过点O的横线所在直线为x轴,过点O且垂直于横线的直线为y轴,相邻横线的间距为一个单位长度,建立平面直角坐标系,如图2所示.当所描的点在半径为5的同心圆上时,其坐标为______.

图2

【解决问题】请帮助小明验证他的猜想是否成立.

【深度思考】小明继续思考:设点P(0,m),m为正整数,以OP为直径画⊙M,是否存在所描的点在⊙M上?若存在,求m的值;若不存在,说明理由.

故存在所描的点在⊙M上,m的值为4.

2 条件探索型

解答条件探索类问题的策略是:从结论出发,逆向追索,补充使结论成立的条件,当然很可能满足结论的条件不唯一.这也正是开放性探索问题的一大特点.具体的解题方法因题而异,具有多样性,值得我们不断探索.

例2(2022年江苏省苏州市中考全真模拟试题第27题)(1)【问题提出】苏科版《数学》九年级(上册)习题2.1有这样一道练习题:如图3①,BD,CE是△ABC的高,M是BC的中点,点B,C,D,E是否在以点M为圆心的同一个圆上?为什么?在解决此题时,若想要说明“点B,C,D,E在以点M为圆心的同一个圆上”,在连接MD,ME的基础上,只需证明______.

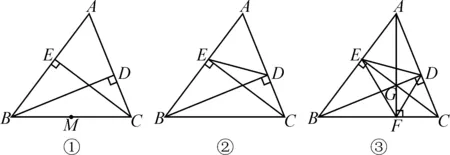
图3

(2)【初步思考】如图3②,BD,CE是锐角三角形ABC的高,连接DE,求证∠ADE=∠ABC.

小敏在解答此题时,利用了“圆的内接四边形的对角互补”进行证明.(请你根据小敏的思路完成证明过程.)

(3)【推广运用】如图3③,BD,CE,AF是锐角三角形ABC的高,三条高的交点G叫做△ABC的垂心,连接DE,EF,FD,求证:点G是△DEF的内心.

解析：(1)根据圆的定义可知,当点B,C,D,E到点M点距离相等时,则它们在圆M上,所以只需证明“ME=MD=MB=MC”.

(2)如图4,取BC的中点M,连接ME,MD.

图4

由BD,CE是锐角三角形ABC的高,可知∠BDC=∠CEB=90°.

在Rt△BDC中,因为M是BC的中点,所以MD=MB=MC.

同理,可得ME=MB=MC.

所以MB=MC=MD=ME.

故四边形BCDE是⊙M的内接四边形.

因此∠EBC+∠EDC=180°.

又∠ADE+∠EDC=180°,所以∠ADE=∠EBC,即∠ADE=∠ABC.

(3)证明:在圆M的内接四边形BCDE中,可知∠CBD=∠CED.

在圆的内接四边形EFCA中,∠CAF=∠CEF.

因为∠CBD+∠ACB=90°,∠CAF+∠ACB=90°,所以∠CBD=∠CAF,则∠CED=∠CEF,即EG平分∠DEF.

同理,可知DG平分∠EDF.

所以点G是△DEF的内心.

思路与方法：本题主要考查了有关三角形、圆的综合问题,熟练掌握三角形、圆的相关知识及证明方法是解题的关键.第(1)问根据圆的定义即可求解.第(2)问根据题意作图4,取BC的中点M,再连接ME,MD;首先求出∠BDC=∠CEB=90°,然后得出MD=MB=MC=ME,即可证明四边形BCDE是⊙M的内接四边形,进而求证即可.第(3)问,首先在圆的内接四边形BCDE中,可知∠CBD=∠CED,在圆的内接四边形EFCA中,可知∠CAF=∠CEF,然后求出∠CBD=∠CAF,即可得出∠CED=∠CEF,进而得出EG平分∠DEF,同理DG平分∠EDF,即可得证.

3 结论探索型

解答结论探索类问题的策略是:采用“执因索果”的思路,从找原因开始,一步步顺推前进.由于解题思路和推导的角度不同,使得答案具有不确定性.

例3(2022年江苏省扬州市中考试题第28题)如图5,在△ABC中,∠BAC=90°,∠C=60°,点D在BC边上由点C向点B运动(不与点B,C重合),过点D作DE⊥AD,交射线AB于点E.

图5

(1)分别探索以下两种特殊情形时线段AE与BE的数量关系,并说明理由:

①点E在线段AB的延长线上且BE=BD;

②点E在线段AB上且EB=ED.

(2)若AB=6.

②直接写出运动过程中线段AE长度的最小值.

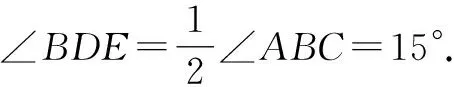
所以∠BDA=90°-∠BDE=90°-15°=75°.

在△ABD中,∠BAD=180°-∠ABD-∠BDA=180°-30°-75°=75°,则∠BAD=∠BDA=75°,所以AB=BD=BE.故AE=2BE.

②如图6,因为BE=DE,所以∠EBD=∠EDB=30°,则∠AED=60°.所以在Rt△ADE中,∠EAD=30°,于是AE=2ED.故AE=2BE.

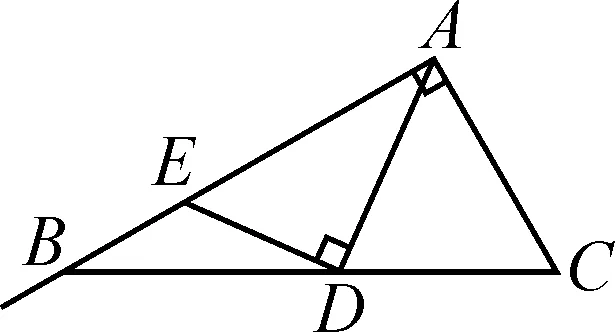
图6

(2)①如图7,分别过点A,E作BC的垂线,垂足分别为G,H,易知△EGD∽△DHA(一线三垂直).

图7

②当∠EAD=30°时,AE最小,且最小值为4.

思路与方法：本题考查几何综合问题,涉及到特殊直角三角形、相似、等腰三角形等知识,有一定的难度;解题的思路与方法主要体现在,能够根据题意作出图7,通过添加辅助线构造“一线三垂直”,运用三角形的相似性质来解决问题.

4 存在性探索型

解答存在性探索类问题的策略是:先假设所探索的对象成立(即存在),再结合题设和已学过的知识进行计算、推理与判断.如果推出的结果符合题目要求,就肯定了存在性;如果推出的结果与题目条件或有关结论矛盾,这样就否定了存在性.

例4(2022年江苏省苏州市中考试题第27题)如图8,在△ABC中,∠ACB=2∠B,CD平分∠ACB,交AB于点D,DE∥AC,交BC于点E.

所以CE=DE=1,△CED∽△CDB.

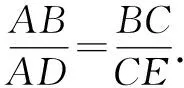
由上述几类探索性问题的解答可知,解答探索性问题的思路与策略是:首先认真审题,在深刻理解题意的基础上,针对不同的题型,从不同的侧面、不同的角度,理清条件和结论之间、图形特征与数式特征之间的关系,然后运用观察、比较、类比、联想、猜想、证明、计算、推断等多种具体方法,进行尝试性解答.Z