结合光学模拟的塑料闪烁体探测器能量刻度

王 超,田华阳,何高魁,赵江滨,刘 洋

(中国原子能科学研究院 核技术综合研究所,北京 102413)

塑料闪烁体探测器广泛应用于辐射探测领域。但由于塑料闪烁体能量分辨率差,并且光电效应截面小,导致塑料闪烁体探测器难以探测到γ射线全能峰,这给塑料闪烁体探测器的能量刻度带来了困难。然而,在一些应用场景中,仍需要对塑料闪烁体探测器进行能量刻度。如利用反电子中微子与质子的反贝塔衰变(IBD)反应探测反电子中微子时,含有大量氢核的塑料闪烁体可作为反电子中微子探测器的灵敏体,这时就需要刻度塑料闪烁体探测器以确定IBD反应产物在探测器灵敏体内的能量沉积数值来进行事件的后续分析,进一步甄别IBD事件[1-2]。

塑料闪烁体主要由碳、氢等低原子序数元素组成,其光电效应截面很小,γ光子在塑料闪烁体内的主要作用方式是康普顿散射。在塑料闪烁体中,光子通常只会发生一次康普顿散射,几乎没有机会发生光电效应,再加上塑料闪烁体能量分辨率极差,导致能谱中不会出现全能峰,只能使用康普顿边沿展宽形成的康普顿峰进行能量刻度。

由于塑料闪烁体极差的能量分辨率,其康普顿边沿展宽形成的康普顿峰并不对应康普顿边沿的能量。为了确定康普顿峰对应的能量,可以简单使用康普顿峰右侧半高值作为康普顿边沿能量,但此时通常误差较大[3-4]。更常用的做法是利用蒙特卡罗模拟得到理想的能量沉积谱,再对理想能谱进行高斯展宽,通过不断调整高斯展宽的参数来逼近真实测量的能谱,根据逼近的模拟能谱中康普顿峰和康普顿边沿之间的关系得到修正因子,对实际能谱进行修正,最终得到康普顿峰的能量[5-9]。也有文献结合人工神经网络,将逼近的模拟能谱作为训练集,直接重建康普顿边沿[10]。

但上述通过高斯展宽计算真实能谱的方法依赖于探测器能量分辨率的经验公式,缺乏对闪烁荧光在闪烁体内传输、收集以及在光电转换器件上光电转换过程的精确描述。GEANT4是欧洲核子中心基于C++面向对象技术开发的蒙特卡罗模拟工具包[11-12],GEANT4提供了可见光光子的输运以及对光学介质和光学表面的参数化描述功能。通过建立闪烁体探测器的光学模型实现对闪烁体探测器更精确的模拟,为研究闪烁体形状及封装等因素对探测效率和能量分辨率的影响提供了手段[13-14],也为模拟真实能谱提供了新的思路。

本文使用GEANT4提供的光学模拟功能对塑料闪烁体探测器进行建模,计算137Cs和60Co的能谱,对比实验测量能谱,验证探测器光学模型的合理性,通过蒙特卡罗模拟能谱最终完成塑料闪烁体探测器的能量刻度。

1 塑料闪烁体探测器建模

反中微子探测器是由图1所示的探测器模块单元组成的阵列,探测器单元模块的灵敏体是尺寸为10 cm×10 cm×100 cm的塑料闪烁体(EJ-200, Eljen Technology),外围包裹反射层/遮光层和单面镀Gd2O3的聚酯薄膜,两端接光电倍增管(CR105-01,北京滨松光子技术股份有限公司)进行双端读出。

图1 单个探测器模块单元结构示意图(a)和实物图(b)

探测器的蒙特卡罗模拟包括两部分:一是射线在塑料闪烁体内能量沉积,塑料闪烁体分子受激后从激发态跃迁到基态导致闪烁发光,闪烁荧光在闪烁体内输运并到达光电倍增管(PMT)的过程;二是闪烁荧光在PMT上的光电转换和光电子倍增的过程。

能谱展宽主要由PMT阳极收集到的电子数的统计涨落决定,阳极收集的电子数可由式(1)表示:

ne=EYphFphεKgcM=npheM

(1)

其中:E为能量沉积值;Yph为光子产额;Fph为光传输和收集效率;εK为光电转换效率;gc为PMT第一打拿极光电子的收集效率,通常可达90%;M为PMT倍增系数;nphe为第一打拿极收集到的光电子数,nphe=EYphFphεKgc。

光电转换效率εK为塑料闪烁体发光光谱与PMT光阴极量子效率的乘积,即:

(2)

其中:QK(λ)为PMT光阴极量子效率;PS(λ)为闪烁体发光光谱;λ为波长。

由式(1)可看出,塑料闪烁体探测器形成输出信号需要经历多个过程,每个过程都会引起输出信号的涨落,导致能量分辨率变差。

输出信号的大小和涨落首先取决于入射粒子损耗的能量和闪烁体的闪烁效率。塑料闪烁体与γ射线作用截面小,不容易沉积能量。同时塑料闪烁体的组成和结构不够均匀,造成能量响应不均匀。塑料闪烁体产生单个荧光光子需要的能量大于半导体探测器和气体探测器产生单个载流子需要的能量,这也决定了塑料闪烁体探测器的能量分辨率与之相比较差。

同时能量分辨率也会受从闪烁荧光的传输和收集以及光电转换效率的大小和均匀性的影响。闪烁荧光在塑料闪烁体内传输和收集是一个效率很低的过程,这使得到达光电倍增管的光子数减少,相对均方涨落增大;若光收集的均匀性不好,不同位置产生相同强度的光会产生不同幅度的输出信号,也会增大相对均方涨落。光电倍增管的光电转换也是一个效率很低的过程。最终只有不足10%的闪烁荧光可以转换成光电子,光电倍增管的第一打拿极还会丢失一部分光电子,倍增系数的不稳定也会影响最终输出信号的幅度。繁琐的输出信号形成过程导致塑料闪烁体的能量分辨率极差。

1.1 GEANT4蒙特卡罗模拟

光电子倍增前的模拟在GEANT4中完成,即射线与物质的相互作用、闪烁荧光的传输以及闪烁荧光的光电转换3个过程。模拟使用的GEANT4版本为10.7,物理列表使用GEANT4内置的参考物理列表QGSP_BIC_AllHP,其中包括电磁物理过程G4EmStandardPhysics_option4和G4EmExtraPhysics,衰变物理过程G4DecayPhysics和G4RadioactiveDecayPhysics。使用衰变物理过程后可以在程序中定义同位素放射源。对荧光光子的产生和处理则引入物理过程G4OpticalPhysics。

模拟中使用的相关物质的关键参数如表1和图2所示。为简化模型,相关物质的光衰减长度和折射率设置为不随波长变化的定值,但事实上这些参数都是随波长变化的。图2中塑料闪烁体的发射光谱为总谱,并没有区分快慢成分,模拟时将此谱作为塑料闪烁体的快成分谱输入程序,没有定义慢成分。对于PMT真空,使用空气的光学参数。

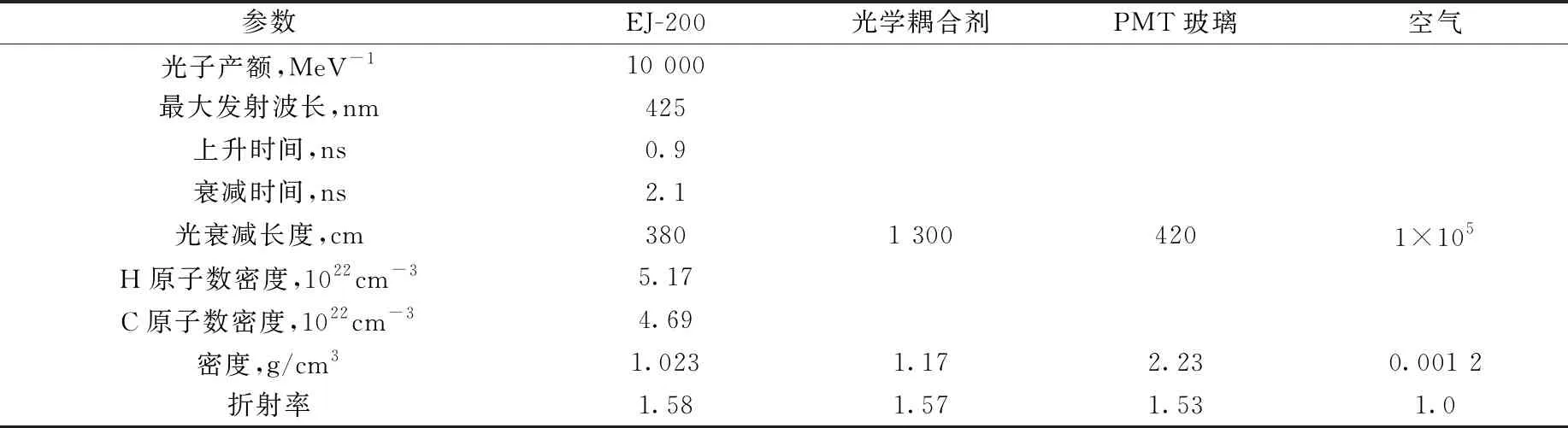
表1 建模所使用相关物质的关键参数

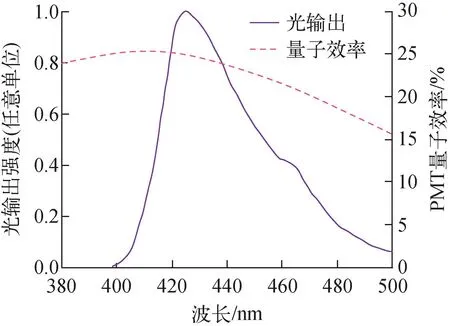
图2 塑料闪烁体发光光谱及PMT光谱响应

塑料闪烁体外围包裹单面镀铝的反射层,在GEANT4中采用内置的UNIFIED模型[15]描述塑料闪烁体和反射层之间的光学表面,介质接触面类型为dielectric_metal,抛光类型为polished,此时只会发生反射与吸收,不发生折射,且反射类型只有镜面反射,通过调整参数与实验测量结果对比,反射概率设置为95%。

塑料闪烁体和光学耦合剂、光学耦合剂和PMT玻璃以及PMT玻璃和空气/真空之间,接触面类型为dielectric_dielectric,由GEANT4依据物质的折射率计算光子的反射和折射等,PMT内部反射面与PMT内真空接触面类型为dielectric_metal,光子到达内部反射面将会发生全反射,PMT的双碱光电面定义为厚度为26 nm的金属薄膜,当有光子到达光电面时就会依据图2中对应波长的量子效率进行光电转换。

1.2 光电子倍增模拟

光电倍增管采用多级倍增系统,其倍增系数为:

M=δ1(gδ)n-1

(3)

其中:δ1为第一打拿极的倍增因子;g为打拿极间电子传输效率,g≈1;δ为除第一打拿极外其余各打拿极倍增因子。各打拿极倍增因子均遵守泊松分布,则M的相对方差为:

(4)

第一打拿极收集到的光电子数nphe应服从泊松分布,倍增后阳极收集到的电子数ne是由光电子数和倍增系数串级而成的串级随机变量,则其相对方差为:

(5)

依据式(5)对倍增后的电子数进行展宽,得到最终的模拟能谱。对于塑料闪烁体探测器,光电子数的涨落是影响能量分辨率的主要因素,倍增系数涨落的影响则小得多。

1.3 放射源定义

在GEANT4程序中定义了两种同位素放射源——137Cs和60Co,这也是在实验中刻度探测器使用的两种放射源。每次事件在探测器中心上方产生一个动量为0的137Cs或60Co粒子,由于衰变物理过程的引入,137Cs或60Co将按照既定衰变路径即时发生衰变。

2 能谱测量

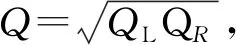
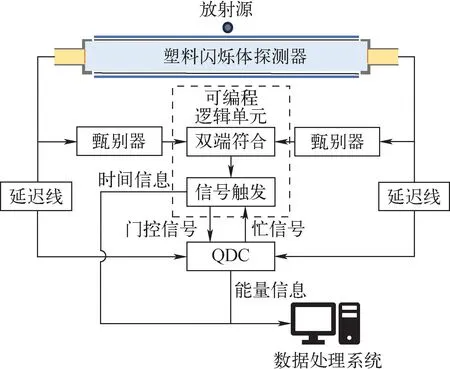
图3 塑料闪烁体探测器系统

使用图3所示探测器系统进行能谱测量,放射源置于塑料闪烁体探测器中心位置。图4为同时使用137Cs和60Co进行测量的实验能谱和蒙特卡罗模拟能谱的对比。从图4可见137Cs的0.662 MeV以及60Co的1.173 MeV和1.332 MeV γ射线形成的康普顿峰,实验能谱与模拟能谱的形状基本一致。

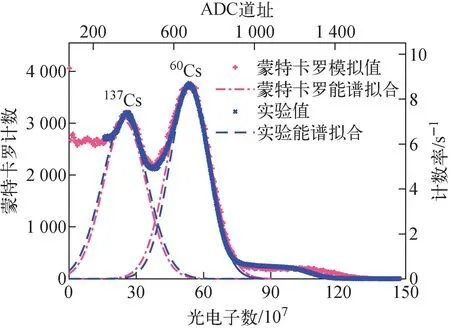
图4 蒙特卡罗模拟与实验测量能谱

在进行能量刻度前,只能对能谱形状进行定性判断,使用双放射源同时进行测量的目的是为了使用多个能量特征峰进行比对,从而避免单个能量特征峰比对带来的偶然相似性。蒙特卡罗模拟能谱与实验测量能谱中不同能量特征峰在相同坐标尺度下的一致性在一定程度上说明了蒙特卡罗模拟能谱是实验测量能谱的足够真实的逼近。同时,由于蒙特卡罗模拟得到的能谱一定是能量线性的,也说明图1所示探测器具有较好的能量线性。

3 结果与讨论

塑料闪烁体探测器能量刻度的基本思想是计算出康普顿峰的能量。使用探测器的光学蒙特卡罗模型计算出光电倍增管阳极电子分布谱,即蒙特卡罗模拟能谱,通过调整光学模型参数使蒙特卡罗模拟能谱逼近实验测量能谱。得到接近实验测量的蒙特卡罗模拟能谱后,便将刻度实验测量能谱的问题转化为刻度蒙特卡罗模拟能谱,而蒙特卡罗模拟能谱可以通过蒙特卡罗模拟计算出实验难以测量的低能γ射线的全能峰进行刻度。

3.1 蒙特卡罗模拟能谱刻度

光电效应、康普顿散射和电子对效应是光子在塑料闪烁体内的3种主要作用方式,图5为3种作用方式的绝对和相对贡献值,反应截面绝对数值由美国国家标准技术研究所的XCOM程序[16]输出的衰减系数结合塑料闪烁体的密度和原子数密度计算得到(XCOM程序输入碳氢比为4.69∶5.17)。由图5可见,对于塑料闪烁体,在20 keV～10 MeV的能量范围内康普顿散射都占据主要地位,100 keV以上的γ光子几乎不发生光电效应。为得到全能峰,使用50 keV以下的γ射线进行模拟,结果如图6所示。由图6可见不同能量γ射线的全能峰以及康普顿边沿,刻度结果如图7所示。拟合结果R2=0.999 9表明低能γ射线模拟结果具有非常好的能量线性,也验证了前文提到的蒙特卡罗模拟得到的能谱是能量线性的。

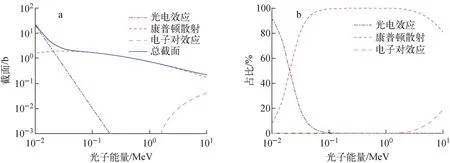
图5 光子在塑料闪烁体内3种主要反应的绝对(a)和相对(b)贡献值

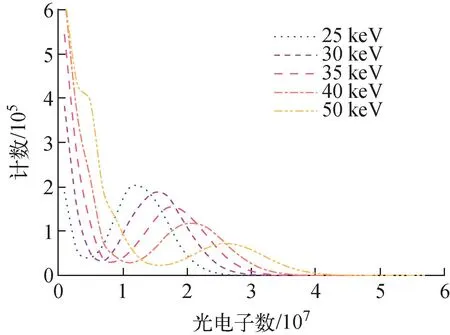
图6 不同能量γ射线的模拟能谱

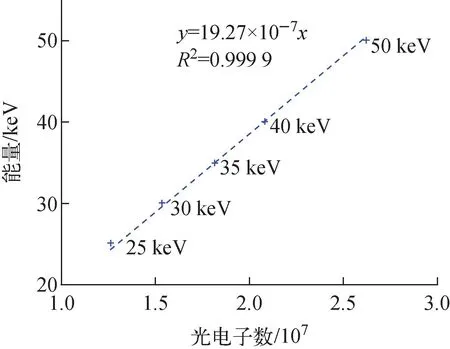
图7 能量与光电子数的刻度曲线

3.2 实验测量能谱刻度

为避免能量较高的60Co的康普顿峰影响能量较低的137Cs的康普顿峰,在进行能量刻度时分别测量二者的能谱。图8、9为使用137Cs和60Co分别进行测量的实验能谱和蒙特卡罗模拟能谱的对比,使用高斯函数对康普顿峰进行拟合,得到其峰位信息,如表2所列。

表2 康普顿峰峰位信息

图8 137Cs蒙特卡罗模拟与实验测量能谱

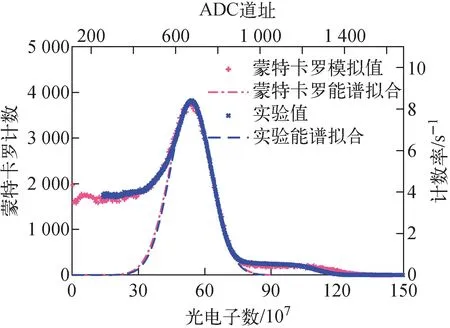
图9 60Co蒙特卡罗模拟与实验测量能谱

结合图7和表2可知,137Cs和60Co康普顿峰对应的能量分别为493.31 keV和1 034.80 keV。得益于探测器良好的能量线性,可以使用一次多项式进行能量刻度,刻度结果如图10所示。由图10可知,QDC每道对应能量为1.80 keV,起始点在98(97.7)道,对于12位(4 096道)QDC可测最大能量约为7.20 MeV。

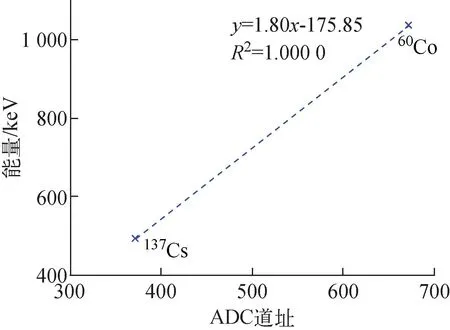
图10 能量与ADC道址的刻度曲线

3.3 刻度结果验证与误差分析

用刻度结果可以反向验证模拟能谱和测量能谱的一致性。模拟能谱和测量能谱的能量分辨率对比如表3所列,可以看到,无论是137Cs还是60Co,模拟能谱和测量能谱的康普顿峰能量分辨率的相对误差均不超过1%。较小的相对误差说明本文所建立的探测器光学模型是对实际探测器的精确建模,也证明了能量刻度结果是可靠的。

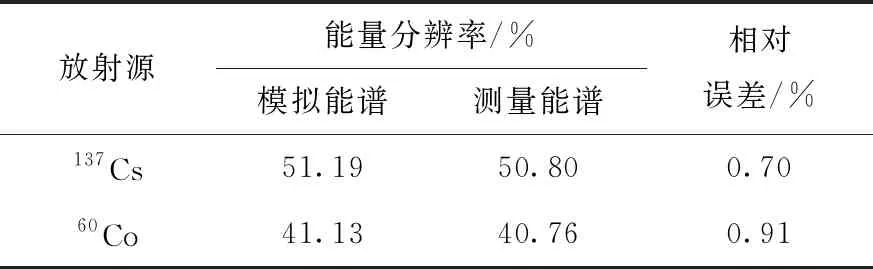
表3 模拟与测量能谱能量分辨率对比

由于塑料闪烁体探测器能量分辨率较差,即使进行了能量刻度,较差的能量分辨率仍可能导致能量测量存在较大误差。较宽的能量峰使得能量测量的精度下降,难以确定入射粒子能量。当2个入射粒子的能量接近时,在能谱中不同能量峰会出现较大的重叠,甚至合并成1个峰,这将导致无法确定入射粒子的能量,因此塑料闪烁体探测器不适用于测量单能粒子能量。事实上塑料闪烁体探测器通常用于粒子强度测量。

4 结论

本文使用GEANT4建立了塑料闪烁体探测器的光学模型,模拟了γ射线在塑料闪烁体探测器内沉积能量、塑料闪烁体闪烁发光、闪烁荧光在塑料闪烁体内的传输、收集以及闪烁荧光在光电倍增管上光电转换和光电子倍增的过程。使用塑料闪烁体探测器的光学模型精确模拟了实验测量能谱,通过计算低能γ射线全能峰位置确定了高能γ射线康普顿峰的能量,完成了探测器的能量刻度。刻度后的蒙特卡罗模拟能谱与实验测量能谱的康普顿峰能量分辨率相对误差小于1%,表明探测器光学模型的精确性和能量刻度结果的可靠性。

与常用的通过高斯展宽模拟真实能谱的方法相比,光学模拟的物理过程更加完备,实现了对闪烁体探测器的精确模拟。但由于光学模拟需要处理大量闪烁荧光的输运过程,由此导致计算时间增加。