颗粒团聚行为对弥散型核燃料芯体失效的影响分析

董颖璇,吕俊男,李 群,*

(1.西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室,陕西 西安 710049; 2.中国核动力研究设计院 反应堆燃料及材料重点实验室,四川 成都 610213)

弥散型核燃料元件是将易裂变燃料相以小颗粒形式弥散分布在相对惰性的非裂变基体材料中的一种混合型燃料元件[1],具有导热性能好、抑制燃料肿胀、包容裂变碎片、阻止裂变物质泄漏等优点,可提高反应堆堆芯的燃耗和安全可靠性[2-3]。然而,现行混料工艺条件无法保证燃料颗粒在芯体中的均匀分布,这必然导致核燃料颗粒在芯体中的局部团聚现象。燃料颗粒团聚将造成弥散型核燃料芯体中局部传热性能变差,颗粒之间的肿胀干涉效应变强,致使芯体更容易在颗粒团聚区域出现裂纹萌生和断裂等失效现象,威胁反应堆堆芯的安全运行。因此,核燃料颗粒在基体中的局部团聚行为(即团聚程度、分布位置等)是影响弥散型核燃料元件性能的关键因素,分析颗粒团聚行为对弥散型核燃料芯体失效的影响可为优化燃料元件设计奠定基础。

颗粒团聚是颗粒增强复合结构中非均匀分布颗粒的局部聚集现象,故燃料颗粒团聚代表弥散型核燃料元件中燃料相的局部非均匀性增加。弥散型核燃料芯体在结构上属于复合结构。颗粒团聚对复合结构的等效力学性能、失效强度、断裂韧性以及损伤行为等[4-7]都有影响,复合结构的断口处裂纹源通常还伴有增强相颗粒的团聚,这种现象可统称为颗粒团聚对复合结构等效力学性能的“短板效应”。颗粒分布均匀性好的复合结构强度高[8],并且颗粒团聚会降低材料的韧性[4]。弥散型核燃料元件的强度和失效同样取决于芯体中的颗粒团聚区域。同时,燃料元件中的应力场受反应堆一回路中冷却剂产生的环境静水压力作用,而环境压力对燃料颗粒团聚“短板效应”的影响尚无定论。为精确评估弥散型核燃料芯体的失效行为,需要分析燃料颗粒团聚行为对芯体应力场的影响,并讨论环境压力对燃料颗粒团聚“短板效应”的作用。

本研究通过构建弥散型核燃料元件的代表性体元(RVE)模型,分析陶瓷燃料颗粒辐照肿胀作用下燃料颗粒团聚对芯体失效的影响。综合考虑数值模型的计算性和收敛性,对三维团聚模型进行合理的等效简化,将非团聚区域进行等效处理,聚焦于燃料颗粒团聚特征(包括团聚体积分数和团聚位置)的影响。其中,非团聚区域的等效处理考虑燃料颗粒和基体材料的热膨胀系数、体积模量和剪切模量。辐照效应考虑基体所受燃料颗粒的辐照肿胀、燃料-基体界面的损伤层(IL)以及随辐照剂量和温度变化的材料性质等因素。弥散型核燃料芯体中的应力场及失效载荷条件主要来源于燃料颗粒的辐照肿胀变形及包壳外的环境压力作用。

本研究针对燃料颗粒团聚行为对弥散型核燃料元件芯体失效的影响展开分析,通过对弥散型核燃料元件团聚RVE模型的数值模拟,揭示燃料颗粒团聚体积分数、颗粒团聚位置、运行环境静水压力等关键因素对芯体失效的影响机理。

1 数值方法

1.1 有限元模型

弥散型核燃料元件的结构如图1a所示,由金属包壳、金属基体和非均匀分布的核燃料颗粒组成。局部燃料颗粒分布间距过近导致的颗粒团聚现象会改变芯体中的应力场分布,进而影响弥散型核燃料元件的失效行为。因此,本研究从弥散型核燃料元件中抽象出RVE模型,通过力学等效过程建立含颗粒团聚行为的RVE模型,等效过程如图1b～d所示。

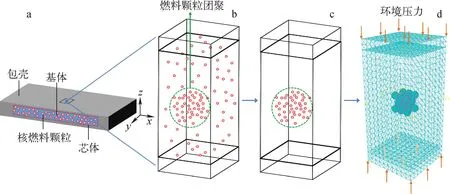
a——弥散型核燃料元件;b——局部弥散型核燃料元件代表性体元模型;c——非团聚区域等效简化的弥散型核燃料元件代表性体元模型;d——网格划分结果

从图1a所示的弥散型核燃料元件中抽象出图1b所示的RVE模型,模型包含上下包壳及弥散芯体两部分。RVE模型在整个燃料元件中所处位置不同,其边界条件也不同。为了聚焦燃料颗粒团聚行为对整个芯体强度的影响,假设每个RVE模型中只存在一个团聚区域,芯体其余部分燃料相等效均匀化。

根据Mori-Tanaka等效理论[9],含非均匀相的复合材料性质可通过等效处理求得其等效材料常数。将图1b中的非团聚区域等效为图1c所示的均匀材料,则材料性质可通过Mori-Tanaka等效理论获得[9-10]。此外,由于复合结构的破坏应力与颗粒间的距离相关[8],图1c所示的团聚区域中采用团聚颗粒的最小间距定义团聚程度。

基体所受燃料颗粒的辐照肿胀压力作用可通过解析方法获得,取代燃料颗粒实体作用于基体内部[11]。由于燃料颗粒裂变产生的固态裂变产物的扩散作用,金属基体和燃料颗粒间存在约5～10 μm的第三相物质损伤层[12-13]。本文在颗粒和基体中间构建了6.5 μm的损伤层模型。同时,上下包壳表面受反应堆中冷却剂流动导致的环境压力作用。有限元模型的网格划分结果如图1d所示,对几何模型中的损伤层进行网格细化,以提高计算收敛性。

1.2 燃料颗粒团聚建模方法

燃料颗粒团聚建模形式有多种,如立方排布和密集堆叠等形式[14],如图2所示。利用图2a所示的立方排布形式计算得到的颗粒团聚体积分数在33%左右,而根据图2b所示密集堆叠排列构建颗粒分布模型的颗粒团聚体积分数相对最高,可达到70%,故本研究采用密集堆叠排列方式进行弥散型核燃料芯体含颗粒团聚特征的RVE建模。

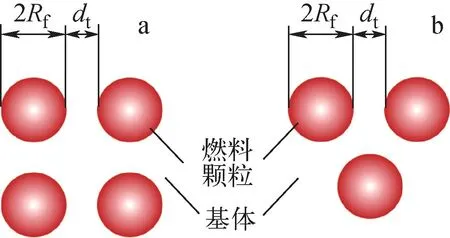
a——立方排布;b——密集堆叠

颗粒团聚程度由团聚区域的最小颗粒间距(dt)定义,根据图2b所示的几何构型与团聚区域的局部燃料颗粒体积分数(Vt)的关系,团聚区域的最小颗粒间距可表达为:

(1)

其中,Rf为燃料颗粒半径。

1.3 非团聚区域等效处理方法

非团聚区域采用等效处理的方法进行均一化(图3),以聚焦燃料颗粒团聚行为对弥散型核燃料芯体失效的“短板效应”影响进行研究。均一化等效处理时,非团聚区域的材料属性根据Mori-Tanaka等效理论[9-10]进行计算。

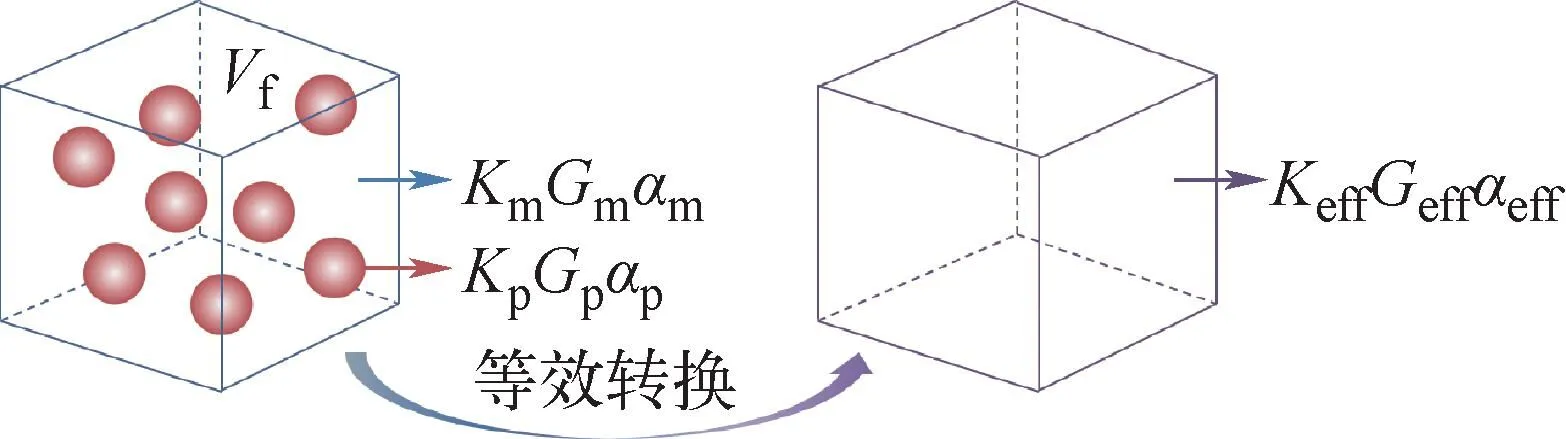
图3 非团聚区域中材料等效转化

根据Mori-Tanaka方法,含异质夹杂的复合结构的等效体积模量(Keff)[9-10]表达式为:

(2)

其中:Km和Kp分别为金属基体和燃料颗粒的体积模量,MPa;Vf为非团聚区域的燃料颗粒团聚体积分数;ξ1为与夹杂形状和位置相关的参数,根据式(3)进行计算。

(3)

等效剪切模量(Geff)采用式(4)[9-10]表征。

(4)

其中:Gm和Gp分别为金属基体和燃料颗粒的剪切模量,MPa;ξ2为与夹杂形状和位置相关的参数,根据式(5)进行计算。

(5)

而等效热膨胀系数(αeff)采用式(6)进行计算。

(6)

其中,αm和αp分别为金属基体和燃料颗粒的热膨胀系数。

1.4 燃料颗粒辐照肿胀模拟

在弥散型核燃料元件中,芯体的应力场因受燃料颗粒辐照肿胀作用和包壳外的环境水压作用而产生。金属基体在燃料颗粒辐照肿胀压力pf作用下变形失效,pf可通过解析模型[11]求解获得。单颗粒辐照肿胀压力解析模型考虑了辐照条件、材料性质以及燃料颗粒高燃耗结构的非均匀分布气孔等因素的影响。为提高含颗粒团聚行为的RVE模型计算性能,采用陶瓷燃料颗粒辐照肿胀的力学解析模型[11]计算基体所受肿胀压力pf,用肿胀压力替代燃料颗粒的作用,使金属基体在肿胀压力pf载荷下变形失效。基体所受陶瓷核燃料球体的辐照肿胀压力pf按式(7)[11]进行计算。

(7)

其中:vf和Ef分别为陶瓷燃料的泊松比和弹性模量(MPa);k0为常系数;BU为燃耗深度,FIMA;f为燃料颗粒气孔率;T为温度,℃;p为气孔内压,MPa,可根据式(8)[15]求解。

(8)

其中:ng、Vg和R分别为裂变气体浓度、裂变气体体积和气体常数;a和b为实际气体状态方程参数。

单颗粒陶瓷燃料中裂变气体的总浓度ng通常满足:

(9)

其中:Df为燃料颗粒密度,g/cm3;ω为裂变气体产额;Mf为陶瓷燃料的摩尔质量,g/mol。

UO2陶瓷具有耐高温、耐辐照、肿胀率低、包容裂变产物性能好等优点,广泛用于设计和生产弥散型燃料元件。另一方面,具有良好力学性能的核级304不锈钢(304SS)是反应堆的关键结构材料,可用作弥散型燃料元件的金属基体和包壳材料。针对UO2燃料-304SS基体这种弥散型核燃料芯体结构,基于式(7)所示的肿胀压力pf表达式,采用UO2陶瓷燃料和304SS的材料参数对pf值进行解析计算和影响因素分析。

温度和燃耗对UO2陶瓷和304SS的弹性模量和泊松比的影响关系[16]如下:

vm(T)=0.3+0.000 05T

(10)

Em(T)=180 000-5.9T-0.124T2

(11)

Ef(T,BU)=162 000+63 000/

(1+BU)-20(T+273)

(12)

其中,vm和Em分别为304SS的泊松比和弹性模量(MPa)。304SS基体和燃料颗粒间的损伤层材料参数取值参考文献[17-18]中的研究结果,不考虑韧性,弹性模量约为基体材料304SS的2倍,泊松比约为基体材料的0.6倍。

在确定了非团聚区域等效材料常数和团聚区域的燃料颗粒建模方法后,为快速生成具有不同团聚程度的弥散型燃料元件代表性体元模型,开发了含颗粒团聚行为的RVE模型的参数化建模脚本,程序流程如图4所示。

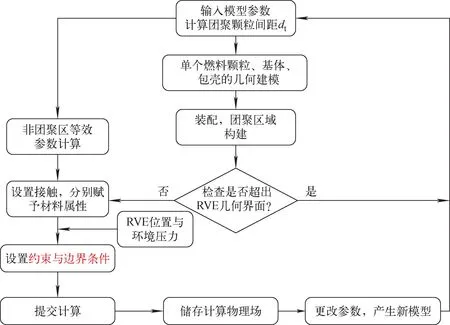
图4 含颗粒团聚行为的RVE模型参数化建模流程

在图4所示的建模流程中,通过输入陶瓷燃料颗粒燃耗、辐照温度、燃料颗粒团聚体积分数和环境压力等参数,可根据式(2)～(6)和式(10)～(12)直接计算不同辐照条件下的材料属性和非团聚区域的等效材料性能,根据式(1)中团聚颗粒间距dt计算结果生成团聚区域的燃料颗粒几何构型,设置损伤层和金属基体间的接触,并将根据式(7)得到的燃料颗粒辐照肿胀压力解析值pf和环境压力q作为载荷条件施加在模型上。约束与边界条件随RVE模型在弥散型核燃料元件中代表位置的不同而改变。最终通过调控关键参数实现具有不同燃料颗粒团聚程度RVE模型的程序化数值计算。

2 数值结果与讨论

2.1 团聚体积分数的影响

燃料颗粒团聚行为主要涉及颗粒的团聚程度和团聚区在弥散型核燃料芯体的分布位置,其中颗粒的团聚程度通过团聚颗粒间距确定。固定陶瓷燃料颗粒的燃耗和温度分别为0.1 FIMA和250 ℃,非团聚区域的燃料颗粒体积分数为10%,弥散型燃料芯体强度分析结果如图5所示。根据计算结果,分别探讨燃料颗粒团聚体积分数、环境压力以及团聚区域位置对芯体失效的影响。

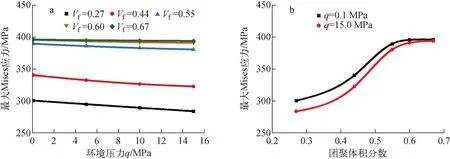
图5 弥散型核燃料芯体强度分析结果

首先,对于代表性体元位于弥散型燃料元件中心的情况,研究燃料颗粒团聚体积分数对芯体中最大Mises应力的影响,计算结果如图5a所示。在不同燃料颗粒团聚体积分数Vf下,最大Mises应力随环境压力q的增加而减小,但不同曲线的斜率不同,即不同团聚体积分数下最大Mises应力的变化率不同。燃料颗粒团聚体积分数的变化范围在(0.27,0.67)区间,环境压力q从0.1 MPa增加至15 MPa。根据计算结果可知,弥散型核燃料芯体中的最大Mises应力随燃料颗粒团聚体积分数的增加而增大。但当燃料颗粒团聚体积分数大于55%时,Mises应力基本不变。故燃料颗粒团聚是弥散型核燃料芯体强度分析的短板。而环境压力会抑制颗粒团聚区域的应力集中,使得芯体的最大Mises应力减小,弥散型核燃料芯体的失效概率降低。但燃料颗粒团聚体积分数越大的模型,最大Mise应力改变量越小,即随着燃料颗粒团聚程度的增加,芯体中应力状态对环境压力的敏感性降低。

由于反应堆中冷却剂循环流动,燃料元件的包壳外不可避免地存在冷却剂诱导的环境压力。环境压力对芯体中最大Mises应力的影响如图5b所示。随着团聚区颗粒间距的增大,燃料颗粒团聚体积分数变大,基体中最大Mises应力随环境压力的改变量非线性减小。当环境压力由0.1 MPa增加到15 MPa时,燃料颗粒团聚RVE模型中基体最大Mises应力分别降低约90 MPa和110 MPa。这是由于颗粒间距更小的模型应力集中程度更强,对环境压力更为敏感。环境压力实际上是对弥散型核燃料芯体的力学约束。但由于环境压力的约束作用与颗粒间距减小的促进作用间相互竞争的影响,不同燃料颗粒团聚程度下芯体最大Mises应力随环境压力的变化率不同。故冷却剂产生的环境压力将提高芯体的安全性,最大Mises应力随环境压力的增大而减小。因此,冷却剂对芯体应力状态的抑制作用对降低弥散型核燃料元件的团聚短板效应具有重要意义。

2.2 团聚区域位置的影响

给定燃料颗粒团聚体积分数为0.27,非团聚区域的燃料颗粒体积分数为0.10,分析燃料颗粒团聚区域位置变化对芯体最大Mises应力的影响规律,结果如图6所示。

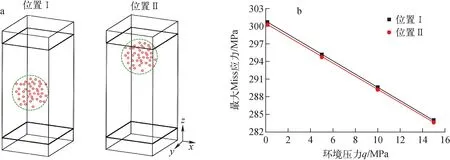
a——两种极限位置示意图;b——极限位置下最大Mises应力随环境压力的变化

该问题将分两种情况进行分析:1) 当RVE模型位于弥散型核燃料芯体中心位置(即只具有上下包壳的结构)时,燃料颗粒团聚区在上下包壳面间沿z轴的位置变化;2) 当燃料颗粒团聚区位于代表性体元中心位置时,考虑RVE模型在整个弥散型燃料元件不同位置变化。

首先,针对RVE模型位于弥散型核燃料芯体中心的情况,研究燃料颗粒团聚区沿z轴位置变化对芯体强度的影响。如图6a所示,在燃料元件的代表性体元中,团聚区域存在两种极限位置:1) 位置Ⅰ,RVE模型中间,最远离包壳的位置;2) 位置Ⅱ,最接近包壳的位置。通过计算不同燃料颗粒团聚位置下最大Mises应力随环境压力的变化(图6b)可知,最大Mises应力随环境压力的增大而减小,不同团聚位置下最大Mises应力的变化趋势相同。故燃料颗粒团聚区域在弥散型核燃料元件上下包壳中的位置对芯体中的应力状态影响不大。

其次,针对燃料颗粒团聚区位于代表性体元中心位置不变的情况,研究RVE模型在整个弥散型核燃料元件不同位置(即团聚燃料颗粒在xy面中位置变化)时的芯体失效行为。RVE模型在弥散型核燃料元件中的位置有3种类型,如图7a所示。3种典型位置下的几何模型不变,通过不同边界条件定义3种位置。

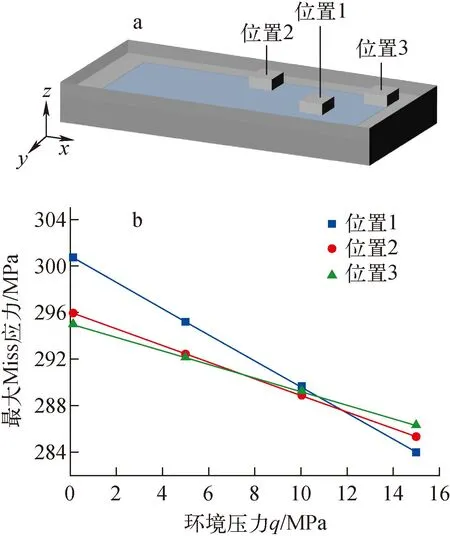
图7 RVE模型在弥散型核燃料元件中不同位置对芯体最大Mises应力的影响

位置1处于芯体中间位置,RVE除包壳上下表面受环境压力外,芯体四周施加对称性边界条件;位置2为单边毗邻包壳,施加单向位移约束边界条件,另外3个毗邻芯体的表面施加对称性边界条件;位置3为弥散型核燃料元件的边角位置,两个相邻表面施加单向位移约束边界条件,另外两个毗邻芯体的表面施加对称性边界条件约束。3个位置RVE模型的最大Mises应力计算结果如图7b所示。

根据计算结果,位置2和位置3中毗邻包壳位置的弥散型核燃料芯体的最大Mises应力基本相等。无环境压力作用时,位置1的Mises应力最大。随着环境压力的增加,所有位置的最大Mises应力均减小,但不同位置的最大Mises应力变化率不同。弥散型核燃料芯体中心位置(位置1)的颗粒团聚对环境压力更敏感,最大Mises应力随环境压力的改变量最大。位置2和位置3的最大Mises应力在环境压力作用下的改变量较小,环境压力对毗邻包壳位置的RVE模型的影响相似。根据强度理论[19],弥散型核燃料芯体中心位置的颗粒团聚位置更容易发生失效。

当环境压力为0.1 MPa时,弥散型核燃料芯体xy面的中心位置(只有上下包壳约束)最大Mises应力最大;当环境压力为15 MPa时,弥散型核燃料芯体xy面的角落位置最大Mises应力最大。故弥散型核燃料芯体的失效行为是环境压力和燃料颗粒团聚分布位置共同影响的结果。

当环境压力小于11 MPa时,位置1的最大Mises应力最大;但当环境压力大于11 MPa时,位置2和位置3的最大Mises应力均大于位置1。这说明在弥散型核燃料元件中,芯体中心位置的应力场对环境压力更敏感,在冷却剂诱导环境压力作用下其安全性提升最多。当环境压力超过11 MPa时,整个燃料元件中不同位置的局部Mises应力集中将被均匀化,抑制到相似的水平。故反应堆一回路中冷却剂产生的环境静水压力可以降低颗粒团聚区域的Mises应力场,提高弥散型核燃料芯体的失效条件,增加反应堆安全性。而燃料颗粒团聚行为是导致弥散型核燃料芯体失效的关键因素,综合分析图5～7可知,当颗粒团聚程度大于65%时,环境静水压力对芯体局部失效将不再有抑制作用,尤其是当团聚位置在图7a所示的毗邻包壳位置时。

2.3 燃料/基体力学性质的影响

将燃料颗粒弹性模量Ef固定,金属基体弹性模量Em作为参考变量,讨论金属基体材料性质对弥散型核燃料芯体失效的影响。通常,陶瓷燃料颗粒的弹性模量大于金属基体,令基体弹性模量Em的取值范围在陶瓷燃料弹性模量Ef的0.83～1.05倍之间变化。

图8为弥散型燃料芯体中最大Mises应力随基体弹性模量Em的变化。由图8可见,芯体中最大Mises应力随基体弹性模量的增加而增大,这与金属基体的相对材料性质变化相关。随着基体弹性模量的增加,芯体所能承受的最大Mises应力升高,弥散型核燃料芯体将更不容易发生失效行为。

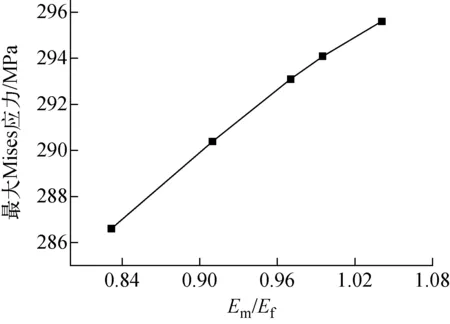
图8 芯体最大Mises应力随基体弹性模量的变化

综上所述,通过建立含局部燃料颗粒团聚体积分数高达0.67的弥散型核燃料元件RVE模型,对弥散型核燃料芯体强度进行了分析,讨论了团聚行为对芯体失效的影响,并综合分析了影响因素及影响机理。燃料颗粒团聚体积分数变大将增强芯体的应力集中现象,使金属基体中的最大Mises应力增大,致使芯体更容易失效。而芯体中的应力场与团聚体积分数并非线性正相关。随着团聚程度的增强,基体中的最大Mises应力逐渐增大,但变化率降低。当燃料颗粒团聚体积分数大于0.6时,团聚对基体最大Mises应力基本无影响。此外,环境压力是影响芯体应力场的重要因素。环境压力主要来源于反应堆一回路的冷却剂,而环境压力降低了芯体中的应力水平,提升了弥散型核燃料元件的安全性。但环境压力的影响对团聚行为非常敏感,随着燃料颗粒团聚体积分数的增大,环境压力对芯体最大Mises应力的影响逐渐减弱,整体呈S型的非线性相关关系。这进一步说明了燃料颗粒团聚区域是弥散型核燃料元件中的短板。

此外,团聚区域位置是影响弥散型核燃料芯体失效的重要因素。金属基体的最大Mises应力与团聚区域在芯体厚度方向(z轴,图1)的位置改变无关,只与燃料颗粒团聚体积分数相关;而团聚RVE模型在弥散型核燃料芯体面内(xy面,图1)区域位置改变会影响芯体最大Mises应力的变化。通过改变模型的边界条件对颗粒团聚位置进行分析,结果表明,最大Mises应力改变量随环境压力而变化,芯体中心位置的应力场对环境压力更敏感,在冷却剂诱导环境压力作用下其安全性提升最多。相比贴近包壳位置的团聚区域,中心团聚区域在环境压力影响下的应力场改变量更大。但无论团聚区域在弥散型核燃料芯体中的位置如何改变,环境压力都降低了芯体内的应力水平。

3 结论

本文通过有限元技术结合Python语言二次开发功能,数值分析了燃料颗粒团聚行为对弥散型核燃料芯体失效的影响机理,结果表明颗粒团聚是弥散型核燃料芯体失效的起点,揭示了燃料团聚现象对弥散型核燃料元件力学性能的“短板效应”,主要结论如下。

1) 随着燃料颗粒团聚相体积分数的增大,弥散型核燃料芯体中的最大Mises应力变大,即芯体更容易失效,但不同颗粒团聚体积分数下最大Mises应力的变化率不同。

2) 堆芯冷却剂的静水压力会降低弥散型核燃料芯体中的应力水平。根据强度理论,环境压力对堆芯安全性提升有正面作用,但局部燃料颗粒团聚体积分数越大,受环境压力的影响越小。

3) 环境压力和燃料颗粒团聚分布位置共同影响芯体的失效行为。而燃料颗粒团聚区域在弥散型核燃料芯体厚度方向的位置改变对芯体失效几乎没有影响。