基于Cholesky分解法的LHS放射性废物处置场安全不确定性分析

赵润才,玉 宇,陈 涛

(华北电力大学 核科学与工程学院,北京 102206)

安全全过程系统分析是保障放射性废物处置设施从选址到建设、运行乃至关闭后安全性的重要手段,近年来,分析过程中的不确定性逐渐受到关注,不确定性分析与管理已成为安全全过程系统分析和安全评价的重要组成部分,国际原子能机构《放射性废物处置安全全过程系统分析和安全评价》、国内《低、中水平放射性固体废物近地表处置安全规定》等文件均对此提出了要求。如何妥善处理安全全过程系统分析和安全评价中的不确定性,将会影响评价结果的可信程度,因此针对长时间尺度的安全评价,开展对案例的不确定性分析研究就显得尤为重要[1-2]。

环境变化、人员行为等事前无法控制的外部因素都将对包含放射性废物处置设施在内的各类核设施的安全产生重大影响,需要对其进行不确定性评估。世界各国以及核行业相关的国际组织均开展了相关的研究,重点关注概率、风险指引、不确定性分析等内容,并根据实际情况开发了一些通用的评价方法,用于不确定性分析,如蒙特卡罗模拟、拉丁超立方抽样等[3-9]。

在放射性废物处置库的不确定性分析中,参数不确定性分析的计算过程相较于常见的蒙特卡罗模拟的运用场景,其涉及输入的随机参数多、运用模型庞杂,势必需求更小的抽样样本以减少运算时间、提高抽样效率。在此情况下,小样本多随机参数的抽样过程必然会涉及一个问题,即抽样样本各维度间的均匀性与相关性能否满足计算所需。

为解决抽样的均匀性问题,采用拉丁超立方抽样(LHS)的蒙特卡罗模拟是常见的选择,本文针对放射性废物处置库安全全过程分析中参数不确定性分析过程,尝试采用Cholesky分解法改进拉丁超立方抽样。经此方法改进的拉丁超立方抽样可以使用更小的样本以满足计算所需的相关性要求,进而提高抽样效率。

1 不确定性分析方法

1.1 拉丁超立方抽样与其存在的问题

为解决抽样的均匀性问题,采用拉丁超立方抽样的蒙特卡罗模拟是常见的选择。该方法已广泛应用于电网计算、飞行器设计、建筑材料设计等领域,是20世纪70年代末,由McKay、Beckman和Conover提出的一种基于分层抽样的多维抽样方法[10-14]。其原理是将样本空间划分成数个独立的子空间,并在每个子空间中随机抽取1个样本点。这样,每个子空间都有1个样本点,而且样本点之间是独立的。其具有每个维度的单个子空间只抽样1次的特点,可减少抽样样本在样本空间的局部聚集,大幅提高抽样的均匀性,进而提高抽样效率。

目前存在的主要问题是拉丁超立方抽样没有解决抽样样本的相关性要求。理想的抽样样本各随机变量间应是相互独立的。这是因为研究中涉及的随机参数之间的相关性可以分为两种:相关性已知的参数和相关性未知的参数。而相关性已知的参数可以进行协变量正交化等方式进行处理以达到相互独立,进而被囊括在同一物理模型中,如处置库中核素的库存量;相关性未知的参数则应假设其为相互独立的。

对于拉丁超立方抽样,其在多维的情况下,会对各维度分别生成一个随机排列,需要生成随机排列矩阵PKN,其每行的元素值代表采样矩阵SKN对应行元素的位置,按照序列对每层进行抽样获得原始样本RKN,再对各独立维度进行整合(图1),即每行的样本按照其在相应行的排列进行映射。

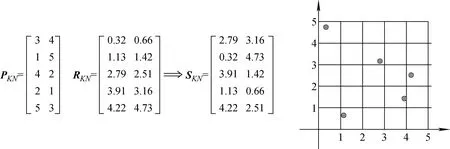
图1 多维情况下拉丁超立方抽样示意图

在此过程会产生一些相关性结构,如排列矩阵中两行元素出现相似的排序,使得部分样本空间没有采样等,如图2所示,此种情况即可称为排序质量低。这种情况会影响抽样样本各维度间的相关性,使得抽样样本的相关性特征偏离计算要求,导致实际计算结果与理论结果的偏差大于预期。这种排序质量低的情形会随样本数量的增加而减轻,为了减少排序质量低的抽样结果对计算结果的影响,需要更多的抽样次数,即抽样效率会降低。

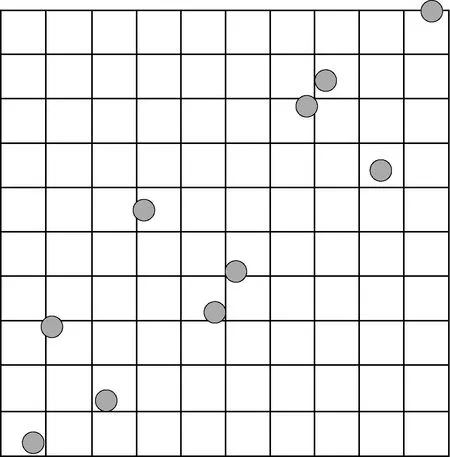
图2 多维情况下低排序质量示例

1.2 改进的方案

本文使用Cholesky分解法协助拉丁超立方法以解决小样本条件下如何满足相关性要求的问题。从本质上,Cholesky分解是一种分解矩阵的方法。Cholesky分解可以把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积。Cholesky分解要求被分解的矩阵为半正定矩阵。如若被分解的矩阵是正定的,则分解结果是唯一的。Cholesky分解已广泛用于金融工程、人工智能等领域,主要用于生成符合要求的独立随机变量,也用于相关的蒙特卡罗模拟与广义最小二乘回归。

本文利用其作为一种降低矩阵各行之间相关性的方法,Cholesky分解的主要思想是:修正排列矩阵PKN,利用Cholesky分解构造近似正交的新排列矩阵GKN,使得各行元素的大小不变的同时,对采样矩阵SKN中各元素的位置进行重新排列,从而降低其行相关性。其本质是将修正前排列矩阵的各行视作具有相关性的另一组随机变量。利用Cholesky分解对PKN进行线性变换,以对其各行向量进行解耦。

排列矩阵PKN的相关系数矩阵ρP是对称且半正定的,可采用Cholesky分解法构造排列矩阵。

半正定性的定义为:任意非零向量x,都有xTAx≥0,则矩阵A为半正定矩阵。对任意随机变量矩阵X={X1,X2,…,Xn},设其均值矩阵为μ={μ1,μ2,…,μn},协方差矩阵为D={d1,d2,…,dn}。

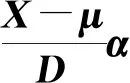
Cholesky分解法构造新排列矩阵GKN的步骤如下:

1) 初始化排列矩阵PKN,该矩阵的每行由整数l,2,3,…,N的随机排列组成,如果原先存在一个排列矩阵PKN,此步骤可跳过。

2) 随机排列矩阵PKN两行之间的相关性可用一个K阶的相关系数矩阵[10]来表示:

ρP={ρij,i=1,2,…,K;j=1,2,…,K}

(1)

ρij为对应两行之间的相关系数:

(2)

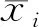
随机变量的相关系数矩阵必然是一个半正定对称矩阵,因此可以对其进行Cholesky分解,得到一个实数的非奇异下三角方阵D,并满足:

ρP=DDT

(3)

3) 由于D是非奇异的,非奇异矩阵必是可逆的,可以利用D-1构造一个列相关性较小的矩阵:

GKN=D-1PKN

(4)

GKN的行相关性小于PKN,由于GKN的元素并非正整数,不能直接作为排序,可以用其中各元素的大小关系作为新的排列顺序,用其大小关系构成的新排列相关性虽与GKN不能等同,但相较于PKN相关性有显著下降。

2 算例分析

2.1 算例的景象设计

本文设计的景象示于图3。该景象是一个低放处置库的事故景象,假定从处置设施关闭后开始评估。基于《核安全法规技术文件放射性废物处置安全全过程系统分析》(NNSA-HAJ-001—2020)中对于模型的分类,本模型属于保守模型。具体景象设定如下。

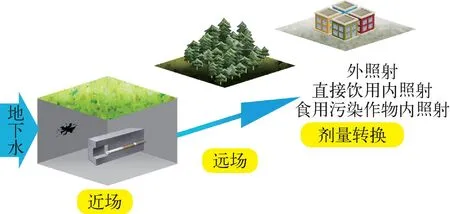
图3 案例景象示意图

1) 处置库遭遇外部突发事件,如地震、地质运动、人类钻探活动等[16-18],导致废物包装破损、工程屏障失效、地下水侵入处置库并将破损废物包装中的放射性核素直接浸出。为便于研究计算方法,相较实际情况进行了简化,其包含的不合理性不影响计算结果对抽样方法的验证。

首先,考虑到500年的核素迁移时长远大于核素从破损废物包装中浸出所需的时间,加之包装破损的形态复杂、破损原因多样,故本文在近场过程中进行了简化,所用模型的浸出过程为直接浸出。

其次,考虑到美国的评估经验,放射性核素在包气带中的流动对处置库的最终性能影响较小,因此在本案例中也忽略核素在包气带中的迁移,而是假设整个处置库都位于地下水的饱和带中,放射性核素直接在饱和带中迁移扩散,且在整个迁移过程中,地下水的流速保持不变。

2) 景象所经历的年限设置为处置库正式关闭后的0～500 年。此时处置库处于无人运行的被动状态,且由于此时包装与屏障已破损,之后的人类入侵事件无法进一步影响后果,故不考虑在此时间点后的人类入侵事件。关于年限的确切起点,本研究参照IAEA给出的处置库案例设定时间框架,认为“处置库彻底封存、正式关闭”即为“取消主动控制”。并依照本研究相关项目任务书的规划要求,将经历年限的考察范围增加至500年。IAEA给出的处置库案例的时间框架如表1[7]所列。

表1 IAEA给出的处置库案例的时间框架

3) 景象考虑了3种放射性核素,分别为129I、137Cs、90Sr,均为常见的核电厂裂变产物。其中,129I是长寿命核素的代表,也是在环境中迁移较快的核素,在低放废物中其活度浓度不超过1 MBq/kg。137Cs和90Sr的半衰期都在30年左右,属于中等寿命核素,在环境中迁移较慢,土壤等介质对这两个核素的吸附能力较强。它们在低放废物中的活度浓度不超过1 GBq/kg。

4) 放射性废物处置场的库存量不定,因此放射性废物的库存量设置为输入参数。

5) 关键人群摄入途径为饮用受污染地下水、接触污染土壤和食用污染农作物3种途径。关键人群距处置库10 km。

2.2 算例公式选取

1) 近场浸出

处置库关闭时,存放的放射性废物中有部分包装有破损。由于处置库在关闭时,工程屏障系统失效,地下水进入处置库,这些地下水接触到包装破损的废物,将其中的放射性核素浸出,放射核素在近场浸出的浓度为:

(5)

其中:CN,i为近场被地下水浸出后核素i在地下水中的浓度,Bq/m3;Qi为核素i在处置库关闭时的存放总量,Bq;FW为进入处置库的地下水流量,m3/a;Ri为核素i的浸出速率,即单位时间内浸出的放射性核素占总量的比例,a-1;η为破损包装的比例。

2) 远场迁移

放射性核素在地质介质中的迁移扩散称为远场迁移。远场迁移的机理较明确,包括地下水的对流输运,污染物的机械弥散、分子扩散,地质介质对放射性核素的吸附、阻滞作用,放射性衰变和其他衰减过程,以及地下水的源、汇项对迁移的影响。本文主要讨论地下水的对流输运、核素的机械弥散、介质对核素的吸附,以及放射性衰变等过程。

一般用对流-扩散方程来描述污染物在地下水中的迁移行为,该方程的形式如下:

(6)

(7)

其中:Rd,i为核素i的阻滞系数,表征核素在固相上的吸附对其迁移行为的影响;Kd,i为核素i在固相介质上的分配系数,m3/kg;ρ为固相介质的密度,kg/m3;θ为固相介质的孔隙率;CF,i为核素i在远场地下水中的浓度,Bq/m3;t为核素迁移时间,a;x为在地下水的流动方向下游距处置库的直线距离,m;u为地下水的流速,m/a,其大小与流入处置库的地下水量有关,计算公式为u=FW/θA,A为处置库处置单元的横截面积(m2);λi为核素i的衰变常量,a-1;I为单位时间单位体积多孔介质中所得到的污染物质量,Bq/(m3·a),反映的是各种源、汇项的作用,若不考虑各种源、汇项的作用,则I=0;DL,i为核素i在地质介质中的弥散系数,m2/a,污染物的水动力弥散包括机械弥散和分子扩散。

机械弥散是由于多孔介质空隙和固体骨架的存在而造成流体的微观速度在空隙中的分布无论是大小还是方向都不均匀的现象。污染物在介质中的机械弥散能力不仅与介质的性质有关,而且与地下水的流动速度有关。当地下水的流速为0 m/a时,不存在机械弥散,则DL,i为核素i在地质介质中的扩散系数。分子扩散是指在浓度梯度作用下,污染物从高浓度向低浓度位置的扩散。

介质中原先不存在129I、137Cs、90Sr,从近场浸出的核素浓度CN恒定,地下水的流速恒定,介质是均匀和各向同性的,迁移发生在地下水流的下游,则上述对流-扩散方程存在如下解析解:

(8)

(9)

3) 剂量转换

由于处置库中放射性核素的迁移,作为饮用水的井水可能会受到污染,直接饮用被污染的地下水会导致人体受到内照射。受地下水污染的影响,周边的土壤中也会出现从处置库中释放出的核素,这些土壤中的核素会对人体产生外照射。农作物从土壤中吸收并累积放射性核素,食用这些农作物人体会受到内照射。根据本文的景象设计,从处置库中释放出的放射性核素对于关键人群的照射途径有3个:一是受污染土壤的直接外照射;二是直接饮用受污染的地下水的内照射;三是食用污染土地上生长的作物所导致的内照射。这3个途径的剂量计算方法如下。

外照射剂量DE,i(Sv/a)的计算公式如下:

DE,i=Cg,iLDFs,iOf

(10)

Cg,i=Kd,iCF,i

(11)

式中:Cg,i为核素i在土壤中的浓度,Bq/kg,主要从污染地下水中通过吸附作用转移而来;L为对外照射剂量有贡献的表层土壤的厚度,m;DFs,i为核素i的外照射剂量的转换系数,(Sv/a)/(Bq/m2);Of为关键人群受土壤外照射的时间份额。

直接饮用受污染地下水所导致的内照射剂量DW,i的计算公式如下:

DW,i=CF,iHWDFW,i

(12)

式中:HW为关键人群每年的饮水量,m3/a;DFW,i为核素i的内照射剂量的转换系数,Sv/Bq。

食用污染土地上生长的作物导致的内照射剂量DV,i的计算公式如下:

DV,i=CV,iHVDFW,i

(13)

CV,i=FV,iCg,i

(14)

式中:CV,i为所食用作物中放射性核素i的浓度,Bq/kg(鲜重),其主要来源于作物从土壤中吸收、富集的放射性核素;FV,i为放射性核素i从土壤中转移到作物中的转移系数;HV为关键人群每年食用作物的量,kg/a。

总剂量Dtot(Sv/a)的计算公式为:

(15)

2.3 算例参数选取

1) 输入参数

根据本案例的景象设置,算例模型分为3个模块,分别是近场浸出模块、远场迁移模块和剂量转换模块。根据模型需求,本文输入参数的取值范围和概率密度分布如表2[16-18]所列。

表2 输入参数的取值范围和概率密度分布

2) 输出参数

本文算例共20个输出参数,其中远场地下水核素总浓度(CF)和总有效剂量(Dtot)是两个最重要的输出参数,其余输出参数分别为各核素在远场地下水中的浓度与按照核素与途径进行区分的有效吸收剂量。

按《低中水平放射性固体废物的浅地层处置规定》(GB 9132—1988)[19]与《生活饮用水卫生标准》(GB 5749—2022)[20]的要求,输出参数CF和Dtot可以作为安全指标。

3 结果分析

3.1 案例结果

为验证本文所提出的方法,以拉丁超立方5 000次抽样结果作为标准,依照算例进行了改进前后500次与5 000次抽样计算。使用拉丁超立方法计算所得各主要参数的均值与标准差如表3、4所列。由表3、4可见,关键人群的总吸收剂量低于《低中水平放射性固体废物的浅地层处置规定》(GB9132—1988)[19]中的0.25 mSv/a剂量限值,地下水核素浓度也低于《生活饮用水卫生标准》(GB 5749—2022)[20]中0.5 Bq/L的总α放射性指标指导值。

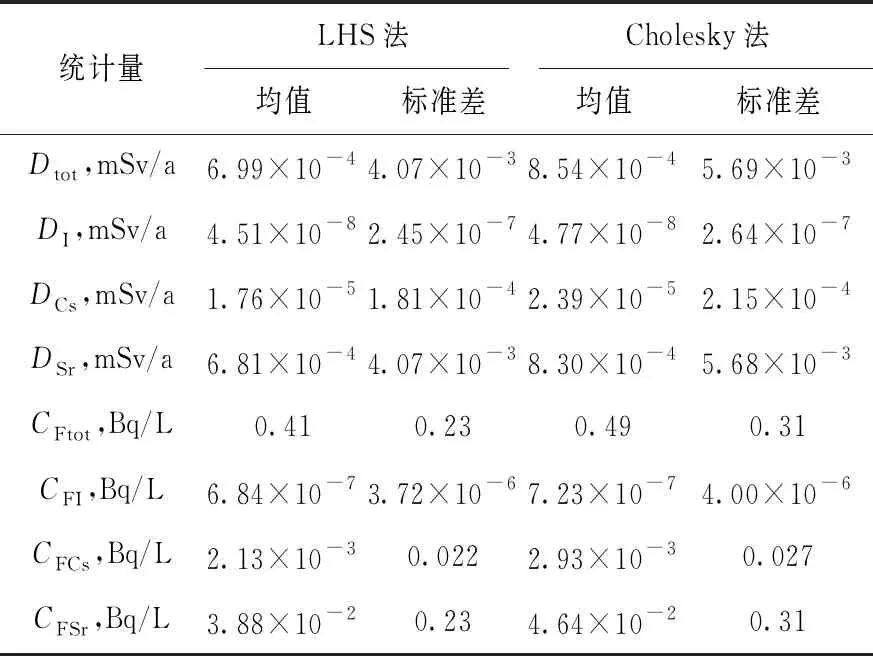
表3 500次抽样下改进前后的计算结果

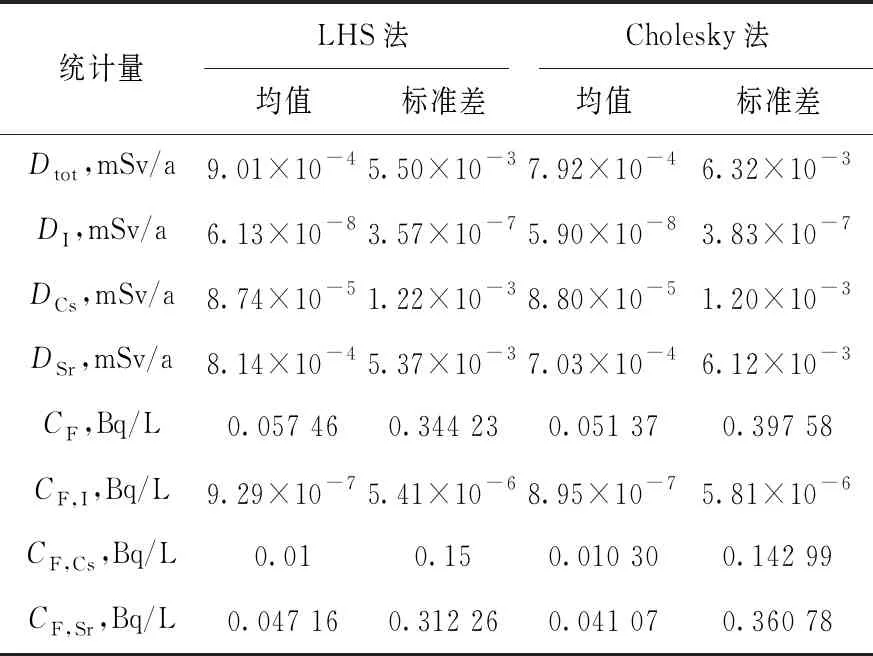
表4 5 000次抽样下改进前后的计算结果

表3、4的绝大多数模拟结果中,CF和Dtot的数值趋近于0是正常的,处置场在设计上应具有较高的保守性。即使景象设定较为严苛,绝大多数情况下也应是安全的,一旦出现极小概率事件才会有一定的危害性,在数据上的表现就是计算结果的变异系数极高,均值较标准差小1个数量级左右。

依照表3、4中的计算结果,并不能判断在本文设定的情境下,处置库的安全水平是否符合标准,引入Cholesky分解法的改进效果也不够直观明显,因此对计算所得结果进一步处理,生成互补累积分布函数(CCDF),以真实判断安全水平与改进结果。5 000次抽样条件所生成的CCDF曲线如图4、5所示。

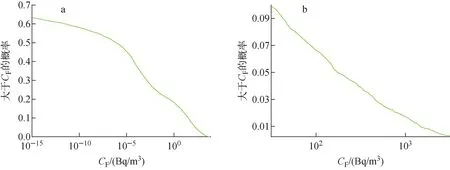
图4 远场地下水中核素浓度的CCDF曲线

对于远场地下水中核素浓度CF,以保守性作为选取标准。以《生活饮用水卫生标准》中对饮用水的要求来约束应足够保守,其对饮用水的要求为总α放射性指标指导值为0.5 Bq/L,总β放射性指标指导值为1 Bq/L,换算后约为500 Bq/m3和1 000 Bq/m3。在以保守性为前提下,以500 Bq/m3为阈值,从图4b可见,大于该阈值的概率约为0.028,即P(CF>500 Bq/m3)=0.028。同样从图4b可见,在95%置信水平下总浓度大致小于200 Bq/m3。

对于吸收剂量Dtot,根据《低中水平放射性固体废物的浅地层处置规定》,其阈值设为0.25 mSv/a。从图5可看出,大于该阈值的概率为0;在95%置信水平下,换算后总剂量大致小于2×10-9mSv/a。

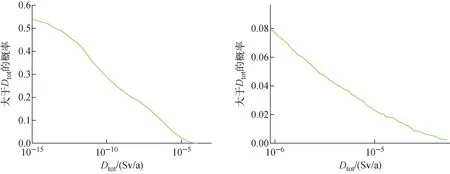
图5 总吸收剂量的CCDF曲线

3.2 改进结果

ρrms可以改进过程对随机变量的相关性影响,较小的相关性代表着更少的相关性结构。故本研究将其引入以评价改进结果。

整体的相关性可用相关系数均方根ρrms表示:

(16)

为了对比改进前后的分析结果,除相关性均方根ρrms外,再引入以拉丁超立方抽样5 000次为基准的误差度指标εμ:

(17)

其中:μ为用于对比的计算结果均值;μacc为作为基准的拉丁超立方抽样5 000次的计算结果。改进前后每个输出参数均可得出一个误差度指标εμ。改进前后的相关系数均方根ρrms及误差度指标εμ列于表5。

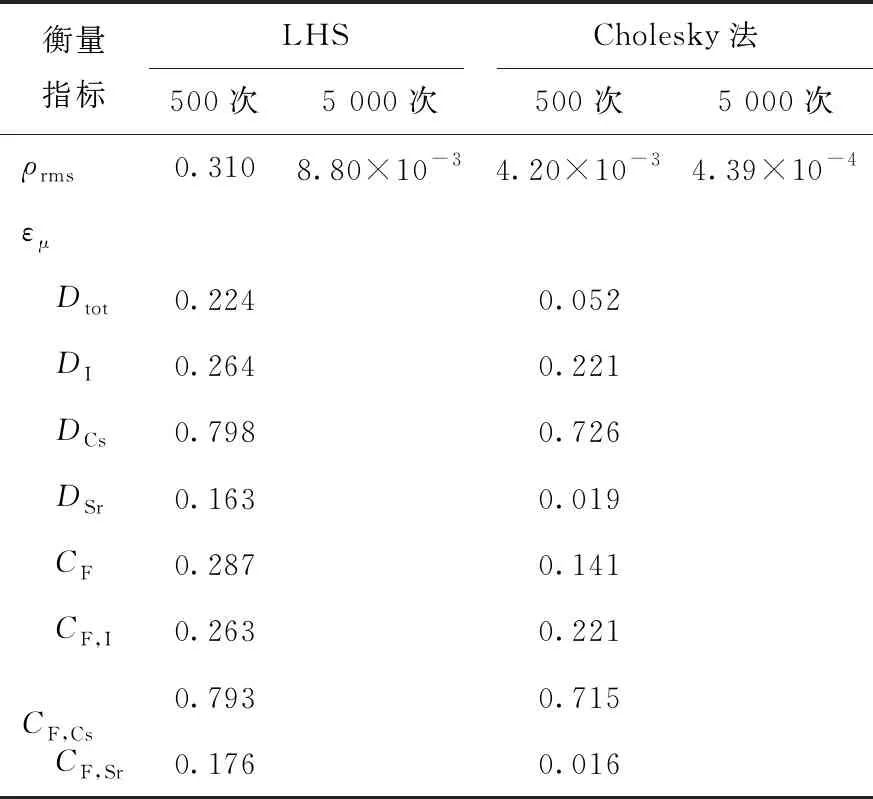
表5 改进前后的衡量指标

在抽样次数相同的情况下,经Cholesky分解法改进前后相关性参数均方根ρrms在500次与5 000次抽样条件下分别由0.310与8.80×10-3下降至4.20×10-3与4.39×10-4。由表3、4可见,改进后CF与Dtot的标准差普遍增大,表明抽样均匀性得到了显著提高。另外,改进后,500次抽样下均值普遍在同一数量级下有所增大,两次抽样测试下标准差均有少量提高。

采用式(19)计算误差度指标εμ,结果示于图6。由图6可见,可以发现经过Cholesky分解法改进后,500次抽样的数据误差显著降低,可以认为其收敛速度得到提升。根据改进前后的结果绘制CCDF曲线,如图7、8所示。

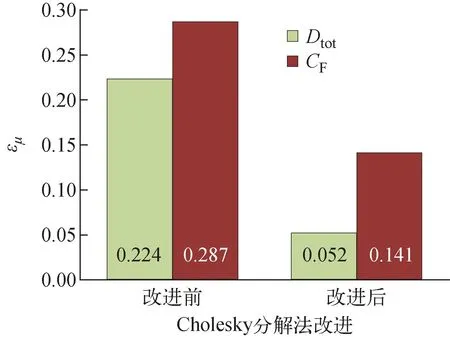
图6 改进前后的误差度对比(以LHS 5 000次抽样为基准)

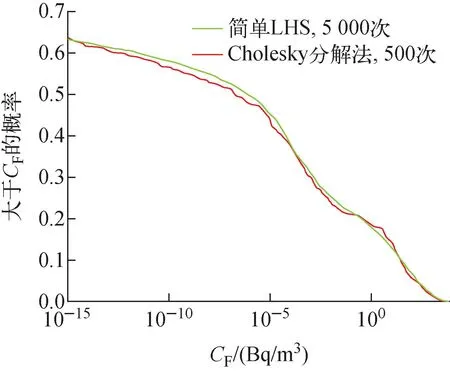
图7 改进前后远场地下水中核素浓度的CCDF曲线

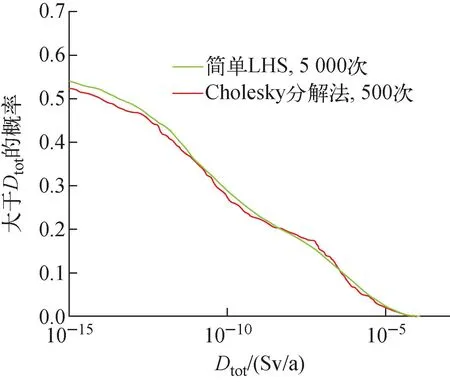
图8 改进前后总剂量的CCDF曲线

由图7、8可见,经过Cholesky分解法改进后的500次抽样条件下的结果与改进前5 000次抽样条件下得出的结果基本一致,各统计特征没有明显差别,可以认为计算结果已收敛。

4 结论

不确定性分析研究中,拉丁超立方抽样并不能解决小样本条件下如何满足相关性要求的问题。在小样本条件下,拉丁超立方抽样的排序质量较低,进而影响抽样效率的问题。为解决此问题,本文采用Cholesky分解法对拉丁超立方抽样进行了改进,使得抽样结果更加满足相关性要求,提高了抽样的排序质量并加速了计算结果的收敛速度。在500次抽样的条件下,经过Cholesky分解法改进后的结果与5 000次抽样条件下得出的结果基本一致,可以认为计算结果已收敛。在本文的使用场景下,改进后的抽样方法只需要使用改进前所需样本规模的1/10即可。