压水堆沉积物对包壳表面性能影响的模拟研究

沈 媛,来允尘,谭诗雨,矫彩山,侯洪国,晁 楠,高 杨,*

(1.哈尔滨工程大学,黑龙江 哈尔滨 150001;2.核电运行研究(上海)有限公司,上海 202150)

一回路结构材料产生的腐蚀产物会在燃料包壳表面沉积,20世纪40年代末,加拿大乔克河实验室最先根据反应堆运行经验命名了这种沉积物,即CRUD(Chalk River Unidentified Deposit)[1-2]。沉积物对反应堆操作和维护的安全性带来的影响越来越重要,其中反应堆产生的最主要的风险来自沉积物中硼累积而造成的沉积物诱导的功率偏移(CIPS)和包壳腐蚀(CILC)。这两种风险都与沉积物存在时压水堆包壳表面传热与传质性能发生的改变有关[3-5]。

从20世纪70年代开始,针对轻水堆中的沉积物传热研究就拉开了帷幕,并形成了一系列以灯芯沸腾为核心的理论和模型研究。灯芯沸腾是基于沉积物结构所作的假设,很多模型均采用该假设来研究沉积物内的传热与流动情况。灯芯沸腾的机理认为沉积物的灯芯结构使得冷却剂能够通过内部颗粒空隙进入到沉积物中发生蒸发换热的表面[6]。沉积物结构和传热机制细化、多物理场模拟拓展、维度拓展和网格划分优化等方面已发展了一系列模型[7-12],并通过实验确定包壳表面的沉积物为多孔且存在烟囱通道[13]。但是,一些研究者发现灯芯沸腾模型计算的结果与实际存在一些矛盾,如Short等[12]报道了灯芯沸腾计算所得的相对实际情况过高的液体过热度,另外,模拟的有效CRUD热导率也与实验结果之间存在矛盾。这可能与灯芯沸腾的假设有关,因为在一般的灯芯沸腾模型中,冷却剂与沉积物界面温度为饱和温度,烟囱通道壁面温度等于饱和温度,而沉积物内全部处于沸腾状态。为了减小模拟结果与实验结果的差异从而使模拟预测更接近实际,Jin等[14]及Yeo等[15-16]考虑了高热通量下沉积物中同时存在灯芯沸腾和膜沸腾的这种过渡状态的可能性,使得沉积物的传热模型计算结果更贴近真实值。然而,理论上CRUD中同时存在非沸腾和沸腾,所计算的过热度将会低于完全沸腾的过热度,但目前缺少同时考虑非沸腾与沸腾的过渡模型。为此,本文提出了基于灯芯沸腾机制优化的过渡传热模型用于预测沉积物中的传热情况。

压水堆中的功率偏移,即AOA现象,被认为主要是因为过冷沸腾导致腐蚀产物在燃料元件上沉积引起的[17]。这是因为沉积物中会隐藏硼物质,无论是以骨架形式组成沉积物,还是由于过冷沸腾使得硼类物质在沉积物的孔隙或烟囱通道中累积,在出现功率偏移时,一个燃料循环周期结束后单根燃料棒的沉积物中所含硼的总质量约为57 mg[18]。而EPRI[19]给出的结果是在一个循环过程中整个堆芯的硼隐藏量约为0.27 kg,会导致轴向偏移率约为-3%,而发生严重功率偏移情况的堆芯中硼累积量约为1.1 kg。根据EPRI给出的评价指标,AOA的偏移率若小于3%,则认为CIPS是低风险的,若接近5%,则认为是中风险的,而若大于10%,则认为是高风险的[20]。对于预测CIPS,准确预估相应条件下包壳表面在沉积物中不同形式的硼累积量至关重要。而针对CILC的模拟预测,文献[21]开发了新的包壳氧化模型,用于预测沉积物导致的包壳表面更大硼锂浓度下的腐蚀行为,并对CILC的风险进行了分析。

因此,本文通过压水堆包壳表面的多物理场过程分析,建立沉积物内部传热、传质、流体流动和化学过程的多物理场耦合模型,预测不同操作条件、水化学条件和沉积物结构下沉积物对包壳表面性能的影响,分析相应情况下沉积物诱导包壳表面传热性能、硼累积风险变化,为堆芯设计、包壳材料开发和运行监测等提供建议。

1 包壳表面多物理过程分析和模拟

1.1 包壳表面沉积物的物理结构分析

燃料包壳表面的沉积物被视为带烟囱的多孔结构,从物理结构上来说,较大的孔或缝隙相连,形成烟囱通道。研究人员通常将多孔沉积物内部的烟囱通道视为均匀分布,选择一个沉积物结构单元来分析内部的物理和化学反应,并进行热量和质量平衡计算。与其他模型一致,本文采用单烟囱及其周围的多孔固体壳层作为沉积物的一个微小计算单元,如图1a所示。为实现模型自动判断沉积物中传热状态,并能够模拟沉积物中包括沸腾和非沸腾在内的过渡情况,设置了沸腾失效线(图中红线)以区分两种机制。需要注意的是,沸腾失效线的位置根据程序在相应情况下对模型进行计算获得。当温度低于饱和温度,即不发生沸腾的区域在红线以上,则这条线以下的区域为沸腾区。当固体壳层中的液体发生沸腾时,气体会汇聚在烟囱中而后向冷却剂流动并重新冷却。

a——沉积物单元;b——沿x正方向的节点与网格划分

1.2 沉积物内部传热与流体流动分析和模拟

灯芯沸腾的传热过程发生在多孔沉积物覆盖的包壳表面,传热介质包括固体壳层、孔隙内液体和烟囱内气体,传热方式包括热传导、沸腾引起的传热和冷却剂与固体界面的对流传热。其中,热传导发生在包围单个烟囱的固体壳层中,而冷却剂在相变导致的流体流动驱动力下通过较小的孔隙被吸入固体壳层中,当温度超过饱和温度时,液体会蒸发成蒸汽从烟囱中逸出。沉积物与冷却剂界面发生对流传热,由于假设蒸汽温度与液体饱和温度相等,因此沉积物内忽略烟囱管道中气体与固体壳层中的对流传热。在灯芯沸腾模型的基础上,文献[22]提出一种过渡模型来解决沉积物计算中被认为液体过热度过高的问题。其中,当温度超过饱和温度时,冷却剂在CRUD的烟囱壁或固体壳层的小孔内发生相变,然后沸腾导致的驱动力将主体冷却剂推入多孔的CRUD中。达到稳态时,液体在沉积物的孔壳中质量守恒,即通过蒸发导致的质量传递和流体流动导致的质量传递进行衡算。

1.3 沉积物内部物质传递与化学过程分析和模拟

1.3.1包壳沉积物内物质传递 对于非挥发性物质传递,需先分析固体壳层中非挥发性物质在沉积物内部的输运。为简化方程,在选择非挥发性物质时忽略了一些浓度特别低的物质,主要考虑沉积物孔壳内液体中含有的锂、硼酸及其三聚体。固体沉积物中溶质的传质形式考虑两种,一种是流体流动的质量传递,另一种是由于浓度差导致的分子扩散过程。非挥发性物质的传递方程参见文献[22]。

文献[22]中,模型未考虑硼酸的挥发过程。由于硼酸具有一定的挥发性,其浓度对饱和温度和腐蚀模拟会产生很大影响,因此本模型考虑硼酸的挥发过程。挥发性物质在固体壳层中的传递过程与非挥发性物质类似,不同的是,需要在温度大于饱和温度的情况下增加气液分离产生的质量传递通量。因此,对于以液体形式存在于固体壳层中的挥发性物质,只需要在非挥发性物质的基础上添加气液分离导致的传递项djp。因此,烟囱中的物质传递项包括3部分,分别是由气液分离引起的传递项djp、由水蒸气流动引起的传递项djm,v以及因为浓度差引起的分子扩散项djc,v。同样,将沉积物中烟囱的网格分成与固体壳层中相对应的边界网格和主网格两部分,每部分挥发性物质的传递过程和方程详见文献[21]。

1.3.2沉积物诱导硼累积过程 有研究者认为仅依靠沉积物Ni2FeBO5不足以导致实际运行中反应堆所达到的AOA值[4]。为探究除了以沉积物骨架的形式在包壳表面发生硼累积外,沉积物形成后诱导硼的再累积过程是否可补充解释AOA现象,对沉积物内部孔隙和烟囱通道中的硼累积过程进行了分析和建模。

1) 沉积物孔隙中硼的吸附

硼对中子的吸收会导致CIPS现象发生,而硼在沉积物中存在的形式主要包括吸附硼、可溶硼、沉积硼。在发生灯芯沸腾的CRUD中,根据Park等[23]的研究,可溶硼在沉积物中的累积量相对于其他两者更大,因此假设在发生硼的吸附和沉积时,溶液中硼的总量变化较小。因此,可溶硼(主要包括硼酸及其三聚体)可直接通过传热模型、流体流动模型和传质模型3个模块计算获得。而吸附硼的量,采用文献中通过对磁铁矿吸附硼的实验获得的Temkin等温吸附曲线进行温度校正计算,当反应平衡时,吸附硼的量qa(B)(mol/m2)由式(1)[24]计算。

qa(B)=k1ln(k2c(B(OH)3))

(1)

k1=A1eE1/T

(2)

k2=A2eE2/T

(3)

其中:c(B(OH)3)为液体中硼酸的浓度,mol/m3;A1=1.938×10-5mol/m2,E1=222.7 K,A2=2.426×10-3m3/mol,E2=859.9 K。

2) 沉积物孔隙中硼的沉积

(1) LiBO2溶解

LiBO2的溶解反应为:

(4)

反应速率方程[25]表示为:

dc(B)/dt=fs(c(Bs))-c(B)/Ksl

(5)

其中:c(B)为LiBO2以离子形式存在的浓度,mol/m3;c(Bs)为LiBO2以未解离分子形式存在的浓度,mol/m3;Ksl为溶解平衡常数,mol/kg,Ksl与温度T(K)的关系可由Byers等[26]在300～360 ℃的实验关系式(式(6))表示;fs为收敛系数,由式(7)[27]计算。

lgKsl=-11.198 85+2 531.538/T+5.112 8lgT

(6)

(7)

计算时,假设溶液中硼酸和锂通过传质导致的浓度变化速率大于化学反应速率,即反应会很快达到平衡。根据EPRI模型计算的数据可知,若硼锂能够沉积,则约10 s即可产生数摩尔的LiBO2[27]。根据硼锂反应方程式,当生成物和反应物的离子积大于该温度下的硼沉积的溶度积,则会产生硼锂沉积物的同时,沉积物空隙中的硼锂浓度也因此更新。因此,在计算网格中的硼沉积之前,首先计算不考虑化学反应时由于物质运输导致的节点物质浓度。其次,根据化学反应式计算离子积Q。

(8)

其中:m为浓度,mol/kg;γo为硼酸活度系数;aw为水的活度。

模型中计算硼累积量时应将溶质的物质传递过程与化学过程同步,由于考虑到硼酸沉积的时间非常快,首先计算不考虑化学反应的硼锂浓度分布,而后通过硼沉积判断硼锂浓缩后是否可能会导致硼沉积。当离子积Q>溶解平衡常数Ksl,则溶液中离子浓度饱和,反应向逆向进行,产生偏硼酸锂沉积物;反之,溶液未饱和,若有LiBO2(s)则会发生溶解,若没有则溶液中不发生沉积。

(2) Li2B4O7的生成

在压水堆中,当发生过冷沸腾,冷却剂中含有大量的硼和锂,硼锂浓度的升高将会发生沉淀反应生成大量的Li2B4O7。当沉积物形成后,沉积物被视作分布着烟囱孔道的多孔结构,为气泡的生成提供了条件。在沉积与释放达到平衡时,Li2B4O7在燃料表面的稳定沉积量主要受到温度、沉积物内流速和硼总浓度的影响。当达到稳态时,Li2B4O7中的硼沉积量WB(g/m2)可通过下式[4]计算。

(9)

其中:MB为硼的摩尔质量,g/mol;ρw为液体密度,kg/m3;ζB为B转换释放速率系数,是一经验值,取0.016 s-1[4];K为沉积速率系数,与气泡的产生和大小有关[28]。

(10)

其中:Rb为最大气泡半径,m;U为气泡产生速率,m/s;μw为流体的黏度,Ns/m2;ρv为水蒸气密度,kg/m3。根据Uchida等[4]的研究可知,RbU项在流体的流速(u)小于2 m/s时,与流速近似呈线性关系,通过对文献数据[29]拟合,可得:

RbU=-0.018 75u+0.016

(11)

3) 总硼累积量计算

根据传热、传质和流体流动模拟计算,可得固体壳层(sh)的包括非沸腾和沸腾的每个网格中的可溶硼量dc(H3BO3)sh(mol/m3)、吸附硼量dc(B)a(mol/m2)和沉积硼量dc(LiBO2)(mol/m3),烟囱通道(ch)的每个网格中的硼酸浓度dc(H3BO3)ch,发生沸腾的固体壳层的每个网格中还会沉积Li2B4O7,硼在该沉积物中的量为dWB(g/m2)。需要说明的是,所考虑的可溶硼、LiBO2和硼酸气体累积区域在沉积物的孔隙和烟囱通道空间中,而吸附硼和Li2B4O7累积的区域是围绕孔隙的固体壳层表面。通过单位换算,可获取附着某一厚度沉积物的燃料棒单位面积所沉积的硼的量(lb,g/m2),如式(12)所示。

dc(LiBO2)+MB(1-f)hdc(H3BO3)ch)+

(12)

其中:1表示沉积物靠近冷却剂的第一个网格;N为靠近包壳处的最后一个网格;j为开始发生沸腾的网格;h为网格宽度,μm;f为沉积物固体孔壳的占比;rp为孔隙半径,取2×10-6μm;2/rp为孔隙的表面积比的简化计算结果,即孔隙的表面积与孔隙的体积之比;ε为孔隙率。

2 包壳表面多物理场模型计算方法

通过迭代计算沉积物多物理过程的方程获取多物理场量的分布。首先,根据沉积物厚度和网格长度计算出沉积物节点数n。假设所有沉积物节点的初始温度为Ts+0.01,液体流速为0,固体壳层中的初始物质浓度等于冷却剂中的对应浓度,烟囱中的气体初始浓度为0。初始化后,通过表示流体流动离散方程的气液体速度模块,重新计算各节点的气液体流速。其次,将新获取的流速数据代入储存流速的矩阵中更新流速参数,并利用包含物质传递方程的浓度模块依次计算固体壳层中的非挥发性物质浓度、固体壳层中的挥发性物质液相浓度和烟囱通道中的挥发性物质气相浓度。更新浓度参数后,利用传热方程的温度模块计算各节点的CRUD温度。重复以上3个主要模块的计算,并比较两次连续计算沉积物所有节点温度的差值。当所有节点的误差小于设置的误差,即0.01 K时,结束计算。需要注意的是,在每次计算后,3个模块中使用的模型参数都会更新。

为实现模型的自适应计算方法,当第i个节点的温度Ti低于饱和温度,而第i+1个节点的温度高于或等于饱和温度时,第i个网格内充满液体,不发生沸腾,则蒸发换热系数接近于0。相应网格的流动驱动力被认为来自于发生相变的第i+1个网格。在这种情况下,认为第i个网格的流速等于i+1个网格的流速。而第i+1个节点中,利用饱和温度计算蒸发换热系数。当沉积物计算所得的平均温度大于临界温度时,用于计算蒸发焓的液体温度假设略低于临界温度,取373 ℃。

图2为沉积物多物理过程耦合计算程序示意图,显示了计算的主要过程以及各模块之间的关系,包括4个主要过程,分别是参数输入、初始化、求解和输出(图2中第2列)。求解部分包括4个模块,分别是流速迭代模块、浓度迭代模块、温度迭代模块和参数更新模块(第3列),用于计算每个节点的温度、气液体速度、挥发性物质和非挥发性物质浓度;第4列表示第3列中各模块使用的函数模块,从上至下,依次计算水蒸气密度、水密度、水蒸发焓、饱和温度、蒸发换热系数、水中溶质扩散系数、水蒸气中溶质扩散系数、气液平衡常数、气相中质量传递系数、沉积物热导率、水的对流换热系数(各参数的计算方程参见文献[21-22])。本文程序采用C语言编写,计算的节点数根据所计算的沉积物厚度而不同,计算网格的宽度取1 μm。沉积物厚度在30～80 μm时,程序计算时长在1～3 min左右。

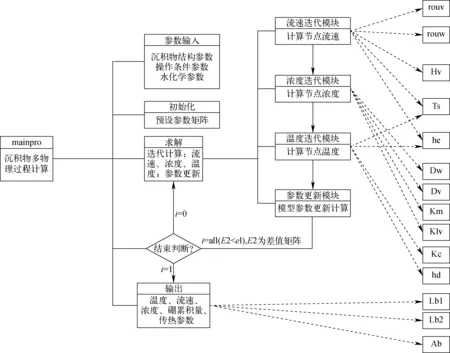
图2 沉积物多物理过程耦合计算的程序模块和函数

3 包壳表面多物理模型验证和结果

3.1 模型验证

为验证模型,本文对WALT回路实验中不同燃料棒实验进行了选择。WALT回路实验报告[13]中,根据实验所得的沉积物烟囱分布和直径将实验燃料棒分成不同组。因此,为更全面地检验沉积物传热传质模型,选取不同组中的实验燃料棒数据和沉积物的结构参数用于计算,热通量的计算范围是从低热通量到略高热通量。不同实验燃料棒中所得的沉积物的烟囱密度、孔隙度、烟囱直径、沉积物厚度和水力直径列于表1。

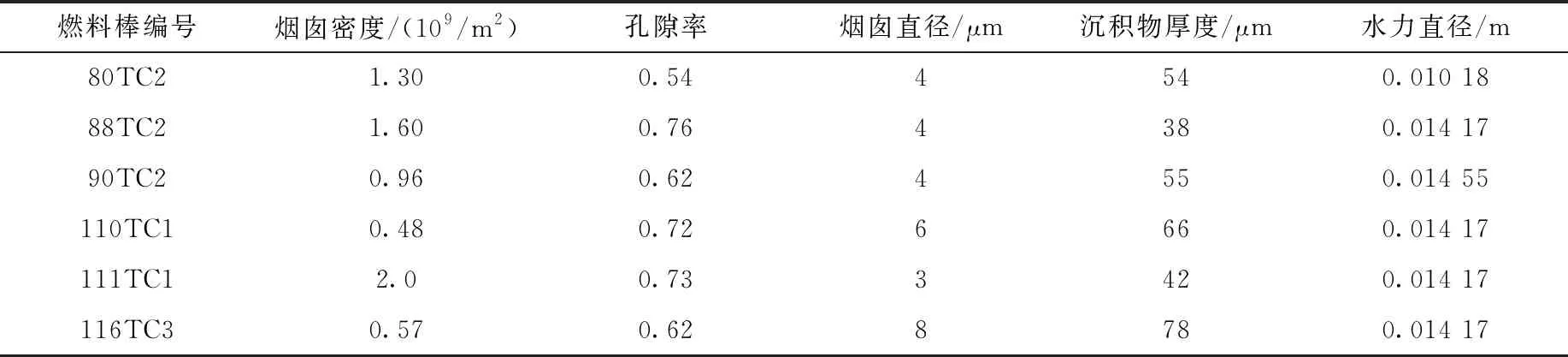
表1 WALT回路实验的燃料棒参数

在WALT回路实验中,当计算的沸腾率小于0.814 kg/( m2·s)时,可认为沉积物中为气液共存,即灯芯沸腾,当计算的沸腾率大于0.814 kg/(m2·s)时,认为沉积物内的孔隙中出现干化[23]。因此,将计算的包壳温度与WALT回路实验中沸腾率小于0.814 kg/(m2·s)时所获取的包壳温度进行对比。另外,目前很多涉及耦合沉积物物质传递的研究中未考虑包壳表面发生过冷沸腾时,沉积物固体壳层的孔隙中硼酸挥发的问题。为此,模型计算了考虑硼酸挥发和不考虑硼酸挥发两种情况下的包壳表面温度,并与WALT回路实验数据进行了对比,如图3所示。从图3可看出,考虑硼酸挥发计算的包壳温度比不考虑硼酸的结果更接近实验值,最大相对误差约为2.7%。

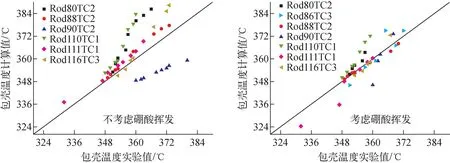
图3 包壳温度计算值与WALT回路实验值的对比

3.2 沉积物对包壳传热性能影响分析

3.2.1包壳温度与传热推动力 沉积物会对包壳表面温度和燃料棒与冷却剂的传热推动力带来一定的影响,传热推动力由冷却剂主体温度和沉积物外界面温度的差表示。沉积物存在时,不同热通量、冷却剂温度、冷却剂硼锂浓度和沉积物结构下,包壳温度相对变化值RT,clad和传热推动力相对变化值RT,force分别用式(13)和(14)计算。

(13)

(14)

当包壳温度相对变化值RT,clad>0时,附着沉积物的燃料棒表面温度高于干净燃料棒,当条件改变时,该值减小,表示附着沉积物的包壳温度变化值小于干净燃料棒的包壳温度的变化值。RT,force>0时,则有沉积物的燃料棒传热推动力比干净燃料棒大,反之,比干净燃料棒的传热推动力大。图4展现了不同条件下所计算的包壳温度与传热推动力的相对值,其中锂浓度和烟囱直径变化对附着沉积物的包壳表面传热影响较小,而热通量、冷却剂温度、冷却剂硼浓度、沉积物厚度、烟囱密度和孔隙率的影响较大。

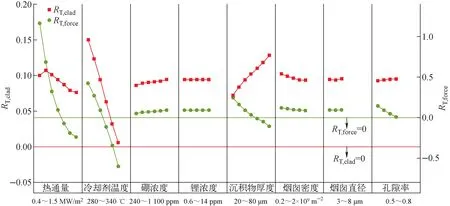
图4 不同条件下包壳温度和传热推动力的变化

沉积物中的传热包括与冷却剂的对流换热、沉积物中的热传导和沸腾传热。如图4所示,对于沉积物存在时所计算的RT,clad大于0,说明沉积物的存在会使包壳温度增加,反映了沉积物对包壳表面热量传递的阻碍作用。另外,相对干净燃料棒,温度剧增程度随着沉积物厚度、硼浓度的增加而增大,随着热通量、冷却剂温度的增加而减小。这是沉积物的存在产生的热阻使得包壳表面的沸腾程度加剧,与沉积物存在导致的硼浓度变化对沸腾换热程度的反作用相制衡的结果。特别需要注意的是,当冷却剂硼浓度增加时,包壳温度略有增加,而RT,clad也增加,这提示提高冷却剂硼浓度会促进沉积物导致的包壳温度剧增效应。这是因为硼浓度会影响冷却剂的饱和温度,当硼浓度增加时,饱和温度增加,而饱和温度是过热度计算中的关键变量,饱和温度升高,过热度(过热度=T-Ts)会减小,从而抑制了沸腾换热过程。根据饱和温度Ts与水活度aw的关系(式(15)),绘制Ts和aw与硼浓缩因子(沉积物中物质浓度相对于冷却剂剧增的倍数[6])的关系曲线,如图5所示。由此可见,硼浓缩因子对饱和温度的影响较大,饱和温度与硼浓缩因子的关系曲线与EPRI报告[27]一致。

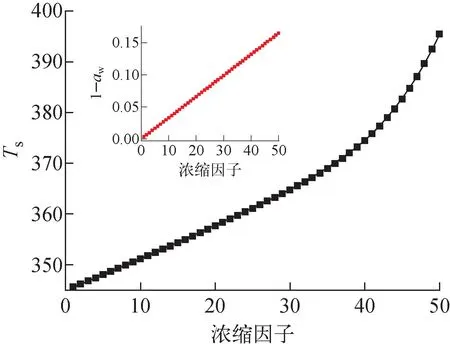
图5 饱和温度和水活度与硼浓缩因子的关系

Ts=344.94+199.01(1-aw)-

952.74(1-aw)2+26 013.91(1-aw)3-

262 916.0(1-aw)4+997 166.1(1-aw)5

(15)

根据图4可知,RT,force反映了有沉积物和无沉积物包壳表面的传热推动力变化情况。RT,force>0时,相对于干净燃料棒,沉积物会加强包壳与冷却剂之间的传热推动力,反之,会减弱传热推动力。当RT,force变大,说明在某条件下,包壳表面在有沉积物时与主体冷却剂的温差变化小于无沉积物时主体冷却剂的温差变化,则传热推动力相对于无沉积物时提高的程度减小。根据计算结果,在沉积物厚度小于50 μm、热通量0.4～1 MW/m2、冷却剂温度小于300 ℃、冷却剂中硼浓度200～1 100 ppm、锂浓度0.6～14 ppm时,相对于干净燃料棒,沉积物的存在会提高包壳向冷却剂的传热推动力;在沉积物厚度大于50 μm、q大于1 MW/m2、Tb大于300 ℃下,相对于干净燃料棒,沉积物的存在会降低包壳向冷却剂的传热推动力。其根本原因是沉积物导致的包壳表面热阻和沸腾程度变化引起的传热变化。当条件变化时,相对于干净燃料棒,传热推动力的提高程度随着冷却剂硼浓度的增加而增加,随着沉积物厚度、热通量和冷却剂温度的增加而减小。锂浓度的变化对传热的影响几乎可忽略。而沉积物的烟囱密度和孔隙率变大时,传热推动力减小。烟囱直径对传热的影响较小。

3.2.2沸腾传热与物质传递 除了沉积物热阻对包壳传热性能影响外,沉积物中发生的沸腾换热作用也不可忽视。为分析沸腾换热过程,除了分析沸腾换热推动力,即过热度、蒸发换热系数变化外,还需要分析沸腾换热的面积,沸腾换热的面积可由本文所提出的沸腾失效率和沉积物厚度计算。物质传递直接受到沸腾程度的影响,沸腾程度越大,物质传递过程越剧烈,物质浓度提高越显著。由于冷却剂中的锂类物质被认为是非挥发性物质,因此其在沉积物中的浓缩因子可反映包壳表面沸腾程度。图6为计算的不同热通量(0.4～1.5 MW/m2)、冷却剂温度(280～300 ℃)、硼浓度(240～1 100 ppm)、锂浓度(0.6～14 ppm)下沉积物底部锂和硼的浓缩因子。计算中,除去目标变量外,其他参数的控制值采用正常压水堆操作条件,即热通量1.0 MW/m2、冷却剂温度300 ℃、系统压力15.5 MPa、锂浓度2 ppm、硼浓度1 100 ppm、沉积物厚度40 μm、烟囱密度2×109m-2、烟囱半径2.5 μm、孔隙率0.6。沸腾过程和物质传递之间存在相互影响的关系,硼酸浓度的提高会对过热度产生影响。不同的条件导致了蒸发换热系数、过热度和沸腾面积的变化,综合结果表现为:当热通量、冷却剂温度和沉积物厚度增大时,沸腾程度总体增大;对于冷却剂温度变化,存在一段平台区;而冷却剂硼浓度增大,沸腾程度减小。导致这些现象的原因如下:热通量变化导致总热量变化,从而引起沸腾程度的变化;冷却剂温度提高导致沸腾程度的变化存在平台段是由于沉积物温度提高和硼浓度提高导致的饱和温度提高,共同制衡的过热度变化引起的;沉积物厚度对沸腾程度影响起主导因素的是传热面积的提高;硼浓度对沸腾程度的制约来源于对过热度的制约。

图6 不同条件下的沉积物硼锂浓缩因子

3.3 沉积物诱导包壳表面硼累积的分析

3.3.1沉积物空隙中的硼累积量 本文中,沉积物中硼的累积形式包括固体壳层溶液中的硼酸、烟囱气体中的硼酸、固体壳层中的吸附硼和沉积硼。因此,本文中硼累积量指的是单位面积不同累积形式的硼质量。不同条件下沉积物空隙中硼累积量的分布如图7所示。从图7可看出,4种形式的硼累积量变化情况相似。不同形式硼累积量会随着热通量、冷却剂温度、冷却剂硼浓度和沉积物厚度的增加而增加,这与Li等[30]模拟的结果趋势一致。当冷却剂中硼浓度从240 ppm增加到1 100 ppm时,可溶硼的累积量提高了2.5倍(图7c),与EPRI中CCM的模拟结果一致。热通量与硼累积量的增加关系近似为抛物线形,当热通量逐渐增大时,硼累积量没有特别大的增幅。而当冷却剂中的锂浓度增加且未达到使LiBO2发生沉积的条件时,锂浓度的增加会一定程度减少硼累积量。

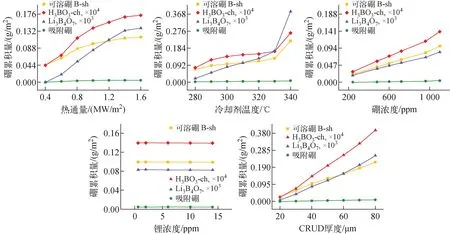
图7 不同条件下沉积物空隙中硼累积量的分布

对于经典的压水堆条件,固体壳层中可溶硼的累积量约为0.057 4 g/m2,烟囱通道中为1.40×10-5g/m2,吸附硼约为4.61×10-3g/m2。50 μm沉积物中,本模型计算的可溶硼量为0.073 g/m2,与同样沉积物厚度下Li等[30]计算所得的可溶硼(0.103 1 g/m2)接近。60 μm沉积物中,模型计算的吸附硼为6.59×10-3g/m2,相同条件下,EPRI的CCM计算的一个烟囱的沉积物计算单元中的吸附硼约为2.3×10-15mol,即根据EPRI的CCM所用的烟囱密度3×109m-2进行单位换算后可得沉积物中吸附硼的量约为6.9×10-3g/m2。因此,模型计算的吸附硼量略小于CCM计算的,这是因为经过模型优化后,本文预测的温度小于原模型,而吸附硼的量随着温度的升高而减小。另外,典型压水堆条件下40 μm沉积物沉积硼的累积量约为8.34×10-5g/m2,主要是过冷沸腾导致的Li2B4O7沉积,由于该值不包括组成沉积物骨架的量,因此不做比较。计算所得沉积物多孔结构和烟囱通道中的硼累积以可溶硼为主,再是吸附硼,而后是沉积硼。

本文计算的硼沉积量主要是沉积物固体孔隙和烟囱通道空间或固液中的硼累积量,不包括组成沉积物骨架中的成分。本模型中,对这两种硼沉积形式的考虑是不同的,对于Li2B4O7,结合了气泡生长破裂原理来模拟硼沉积的过程。而对于LiBO2,主要考虑其发生化学反应沉积的过程,通过对比溶度积与离子积发现LiBO2的沉积反应不发生。在以往的灯芯沸腾模型中,由于假设沉积物中所有区域都会发生沸腾,所计算的温度偏高,如CCM,假定冷却剂与沉积物界面的温度为饱和温度,在60 μm沉积物中计算所得的沉积物与包壳界面温度接近385 ℃,这种情况下LiBO2才会发生沉积[31]。对传热模型优化后,所计算的过热度更合理,而沉积物温度也比以往模型更低,因此更接近实验值,温度越小,LiBO2的溶解度越大,这就导致对于优化后的模型,即使沉积物中的Li+和B(OH)3浓缩后,依然不足以使这种化合物沉积。这种现象也与以往实验中无法重现LiBO2的情况[32]一致。

3.3.2沉积物诱导硼累积的风险关系式 根据沉积物形成后诱导硼再次累积的过程分析和模型计算,获取了不同条件下沉积物空隙中不同形式硼累积量,包括沉积物孔隙中的硼酸和烟囱通道中的硼酸、孔隙中发生沉积的硼和被吸附在固体壳层中的硼,但不包括组成沉积物骨架的沉积硼。根据EPRI给出的堆芯中累积270 g硼会引起功率偏移-3%,对不同条件下沉积物诱导硼累积的量所引起的风险进行估算。由于沉积物一般被认为在堆芯的上部分区域,此处取沉积区域为堆芯的1/8处,参照发生AOA现象的美国Callaway电厂第9循环周期的燃料棒表面积数据(7 706.8 m2)[25],则用沉积物诱导硼累积引起的功率偏移量衡量风险值,即沉积物诱导硼累积的风险估算如下:

Rlb=-Klb·lb

(16)

式中:Rlb为风险值;Klb=3%×7 706.8/(8×270)=0.107。

不同条件下沉积物中的硼累积量和所增加的瞬时风险值如图8所示。

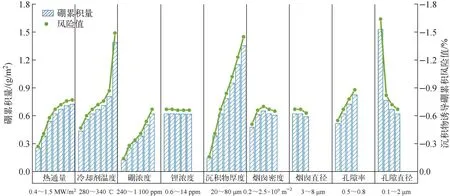
图8 不同条件下沉积物空隙中的硼累积量和诱导的风险值变化

通过多元线性拟合分析不同因素下的数据,可获取沉积物诱导包壳硼累积风险值与主要影响因素之间的关系,如式(17)所示。

Ylb=∑RiFi+E

(17)

式中:Ylb为归一化后的沉积物诱导包壳硼累积的风险值;Ri为回归系数;Fi为归一化后的影响因素,影响程度较大的因素包括热通量、冷却剂温度、硼浓度、沉积物厚度、烟囱密度、孔隙率和孔隙直径。

式(17)的各项式展开后如式(18)所示。

0.238 07

(18)

式中:q为热通量,MW/m2;Tb冷却剂温度,℃;c(B)为冷却剂中的硼浓度,ppm;δ为沉积物厚度,μm;Nc为烟囱密度,109m-2;rp为孔隙直径,μm。

4 总结

本文通过对附着沉积物的包壳表面传热、传质、流体流动、化学过程进行分析和建模,迭代计算了包壳表面多物理耦合模型。在对包壳表面的多物理过程模型优化和计算后,探讨了各物理过程之间的耦合关系,定义了用于评估包壳表面沉积物诱导硼累积的风险值,分析了不同条件下沉积物对包壳表面传热性能的影响和沉积物诱导的硼累积风险变化,通过对比包壳表面多物理过程模型结果与美国西屋公司WALT回路实验结果,验证了优化后的模型能够更真实预测附着沉积物的包壳表面性能。通过分析讨论,沉积物对包壳表面性能影响表现如下。

1) 沉积物存在导致了包壳表面温度剧增,沉积物存在时计算的RT,clad均大于0。温度剧增程度随着沉积物厚度、硼浓度的增加而增大,随着热通量、冷却剂温度的增加而减小。导致此现象的原因是,沉积物的热阻使得热量难以更快地从包壳表面传输到主体冷却剂,从而使得包壳表面沉积物中的液体温度升高更快,导致沸腾程度加剧。而温度升高又加剧液体蒸发导致硼浓缩,造成饱和温度升高从而影响过热度。

2) 相对于干净燃料棒,在沉积物厚度小于50 μm、热通量0.4～1 MW/m2、冷却剂温度小于300 ℃时,沉积物的存在会提高包壳向冷却剂的传热推动力;在厚度大于50 μm、热通量大于1 MW/m2、冷却剂温度大于300 ℃时,沉积物的存在会降低包壳向冷却剂的传热推动力。

3) 硼在沉积物孔隙和烟囱通道中累积导致的功率偏移的风险与不同条件对温度、沸腾程度和硼酸挥发过程的影响有关,还与沉积物结构参数导致的硼累积区域变化有关。对于经典的压水堆条件,40 μm沉积物微孔结构中,硼累积量主要来源于硼酸浓集(0.057 4 g/m2)和吸附硼(4.61×10-3g/m2),孔道中沉积硼来源于Li2B4O7预估值,为8.34×10-5g/m2,而LiBO2的热力学计算结果表明本文计算的条件范围内无法发生沉积。